Chapter 4 The Mean and Variance 4 1














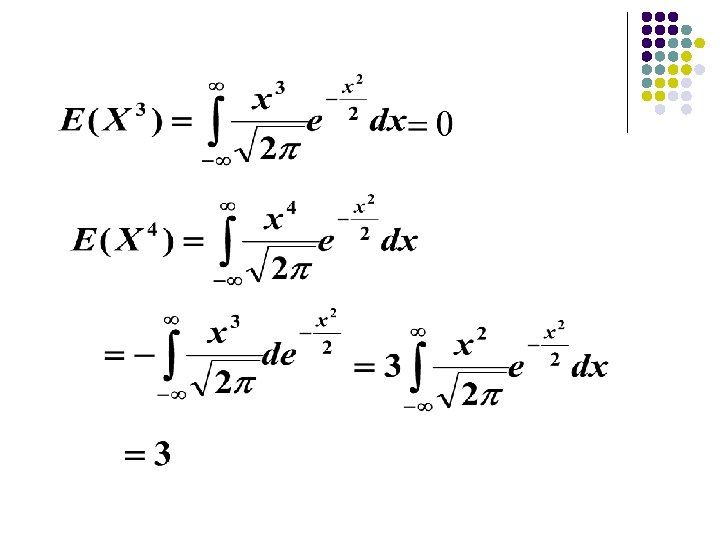




- Slides: 19

Chapter 4 The Mean and Variance 4. 1 Expectations of random variables

Although all the probability information of a random variable is contained in its cdf (or pmf for discrete random variables and pdf for continuous random variables), it is often useful to consider various numerical characteristics of that random variable. One such number is the expectation of a random variable; it is a sort of “weighted average” of the values that X can take. Here is a more precise definition.

Mathematical expectation Definition 4. 1 If X~P{X=xk}=pk, k=1, 2, …n, define the mathematical expectation of r. v. X or mean of X. Example 1 Find EX if X is the outcome of a toss of a fair die. Since P(X =1)=. . . = P(X =6)=1/6, we have Note: E(X )is not necessarily a possible outcome of the random experiment as in the previous example.

Mathematical expectation of several important distributions 1. 0 -1 distribution E(X)=p

2. Binomial distribution X~B(n, p)

3. Poisson distribution

Definition 4. 1 Suppose that X~f(x), - <x< , then define the mathematical expectation of r. v. X Example : P 74 - Example 4. 3

Mathematical expectation of several important distributions 1. Uniform distribution X~U(a, b)

2. Exponential distribution X~Exp()

3. Normal distribution X~ N( , 2)

Mathematical expectation of the functions of r. v. s EX 1 Suppose that the distribution law of X X Pk -1 0 1 Try to determine the mathematical expectation of Y=X 2 Y Pk 1 0

P-74 Theorem 4. 1 let X~P{X=xk}=pk, k=1, 2, …, then the mathematical expectation of Y=g(X) is given by the following equation and denoted by E(g(X))

P-74 Theorem 4. 1 If X~f(x), - <x< , the mathematical expectation of Y=g(X) is specified as

Suppose that X follows N(0,1) distribution, try to determine E(X 2), E(X 3) and E(X 4)
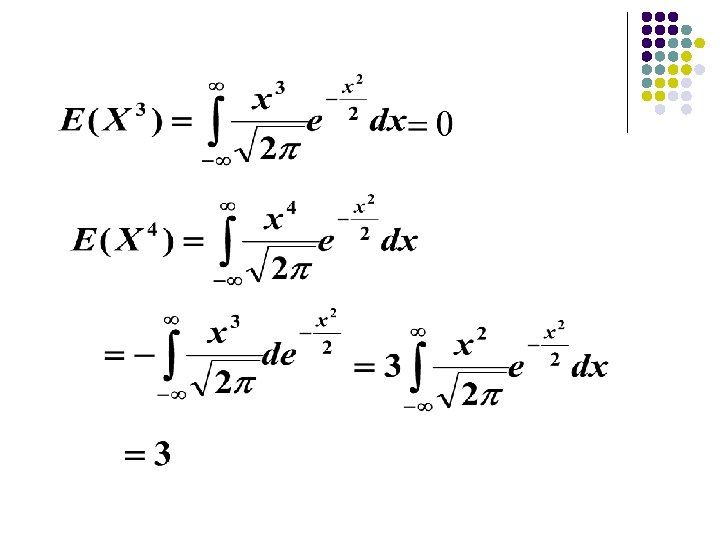

Properties of mathematical expectation 1. E(c)=c, where c is a constant; 2。E(c. X)=c. E(X), c is a constant. Proof. Let X~f(x), then

Example 2. Some disease will occur with probability 1%, investigate 1000 people now, it is necessary to check the blood. The method is clarified these people into ten group with each group 100 and check the mixed blood sample. If the result is negative, it is not need to do any test any more, if it is positive, then , it is necessary to test each blood sample respectively, try to determine the average times needed for the test. Let Xj is the number to be taken of jth group, and X the number to be taken in 1000 people, then Xj Pj 1 101


Homework: P 88: 1(2)(3)(4)(5), 10 Find the mean