Chapter 4 The Exponential and Natural Logarithm Functions

Chapter 4 The Exponential and Natural Logarithm Functions Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 1 of 55

Chapter Outline q Exponential Functions q The Exponential Function ex q Differentiation of Exponential Functions q The Natural Logarithm Function q The Derivative ln x q Properties of the Natural Logarithm Function Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 2 of 55

§ 4. 1 Exponential Functions Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 3 of 55

Section Outline q Exponential Functions q Properties of Exponential Functions q Simplifying Exponential Expressions q Graphs of Exponential Functions q Solving Exponential Equations Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 4 of 55

Exponential Function Definition Example Exponential Function: A function whose exponent is the independent variable Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 5 of 55

Properties of Exponential Functions Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 6 of 55

Simplifying Exponential Expressions EXAMPLE Write each function in the form 2 kx or 3 kx, for a suitable constant k. SOLUTION (a) We notice that 81 is divisible by 3. And through investigation we recognize that 81 = 34. Therefore, we get (b) We first simplify the denominator and then combine the numerator via the base of the exponents, 2. Therefore, we get Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 7 of 55

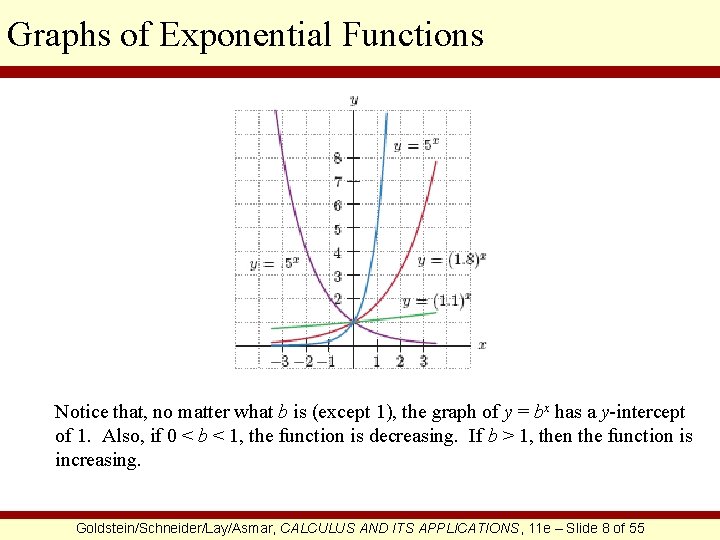
Graphs of Exponential Functions Notice that, no matter what b is (except 1), the graph of y = bx has a y-intercept of 1. Also, if 0 < b < 1, the function is decreasing. If b > 1, then the function is increasing. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 8 of 55

Solving Exponential Equations EXAMPLE Solve the following equation for x. SOLUTION This is the given equation. Factor. Simplify. Since 5 x and 6 – 3 x are being multiplied, set each factor equal to zero. 5 x ≠ 0. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 9 of 55

§ 4. 2 The Exponential Function e x Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 10 of 55

Section Outline q The Derivatives of 2 x, bx, and ex Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 11 of 55

The Number e Definition Example e: An irrational number, approximately equal to 2. 71828, such that the function f (x) = bx has a slope of 1, at x = 0, when b = e Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 12 of 55

The Derivative of 2 x Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 13 of 55

Solving Exponential Equations EXAMPLE Calculate. SOLUTION Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 14 of 55

The Derivatives of bx and ex Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 15 of 55

Solving Exponential Equations EXAMPLE Find the equation of the tangent line to the curve at (0, 1). SOLUTION We must first find the derivative function and then find the value of the derivative at (0, 1). Then we can use the point-slope form of a line to find the desired tangent line equation. This is the given function. Differentiate. Use the quotient rule. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 16 of 55

Solving Exponential Equations CONTINUED Simplify. Factor. Simplify the numerator. Now we evaluate the derivative at x = 0. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 17 of 55

Solving Exponential Equations CONTINUED Now we know a point on the tangent line, (0, 1), and the slope of that line, -1. We will now use the point-slope form of a line to determine the equation of the desired tangent line. This is the point-slope form of a line. (x 1, y 1) = (0, 1) and m = -1. Simplify. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 18 of 55

§ 4. 3 Differentiation of Exponential Functions Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 19 of 55

Section Outline q Chain Rule for eg(x) q Working With Differential Equations q Solving Differential Equations at Initial Values q Functions of the form ekx Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 20 of 55

Chain Rule for eg(x) Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 21 of 55

Chain Rule for eg(x) EXAMPLE Differentiate. SOLUTION This is the given function. Use the chain rule. Remove parentheses. Use the chain rule for exponential functions. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 22 of 55

Working With Differential Equations Generally speaking, a differential equation is an equation that contains a derivative. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 23 of 55

Solving Differential Equations EXAMPLE Determine all solutions of the differential equation SOLUTION The equation has the form y΄ = ky with k = 1/3. Therefore, any solution of the equation has the form where C is a constant. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 24 of 55

Solving Differential Equations at Initial Values EXAMPLE Determine all functions y = f (x) such that y΄ = 3 y and f (0) = ½. SOLUTION The equation has the form y΄ = ky with k = 3. Therefore, for some constant C. We also require that f (0) = ½. That is, So C = ½ and Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 25 of 55

Functions of the form ekx Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 26 of 55

§ 4. 4 The Natural Logarithm Function Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 27 of 55

Section Outline q The Natural Logarithm of x q Properties of the Natural Logarithm q Exponential Expressions q Solving Exponential Equations q Solving Logarithmic Equations q Other Exponential and Logarithmic Functions q Common Logarithms q Max’s and Min’s of Exponential Equations Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 28 of 55

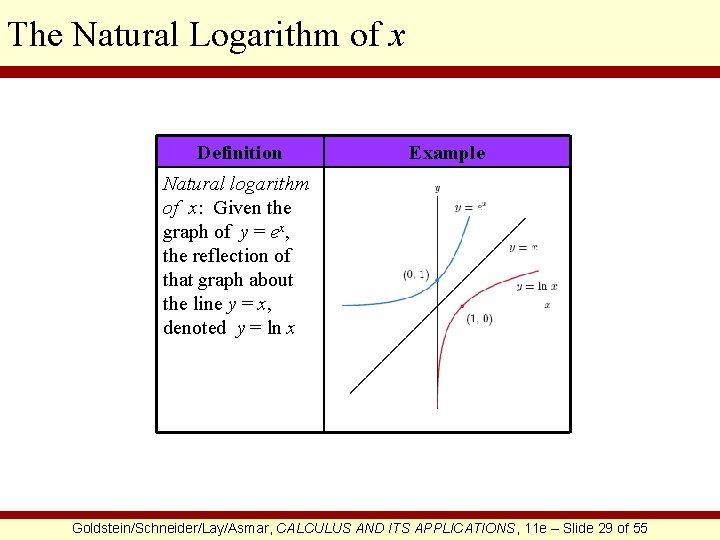
The Natural Logarithm of x Definition Example Natural logarithm of x: Given the graph of y = ex, the reflection of that graph about the line y = x, denoted y = ln x Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 29 of 55

Properties of the Natural Logarithm Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 30 of 55

Properties of the Natural Logarithm 1) The point (1, 0) is on the graph of y = ln x [because (0, 1) is on the graph of y = ex]. 2) ln x is defined only for positive values of x. 3) ln x is negative for x between 0 and 1. 4) ln x is positive for x greater than 1. 5) ln x is an increasing function and concave down. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 31 of 55

Exponential Expressions EXAMPLE Simplify. SOLUTION Using properties of the exponential function, we have Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 32 of 55

Solving Exponential Equations EXAMPLE Solve the equation for x. SOLUTION This is the given equation. Remove the parentheses. Combine the exponential expressions. Add. Take the logarithm of both sides. Simplify. Finish solving for x. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 33 of 55

Solving Logarithmic Equations EXAMPLE Solve the equation for x. SOLUTION This is the given equation. Divide both sides by 5. Rewrite in exponential form. Divide both sides by 2. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 34 of 55

Other Exponential and Logarithmic Functions Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 35 of 55

Common Logarithms Definition Example Common logarithm: Logarithms to the base 10 Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 36 of 55

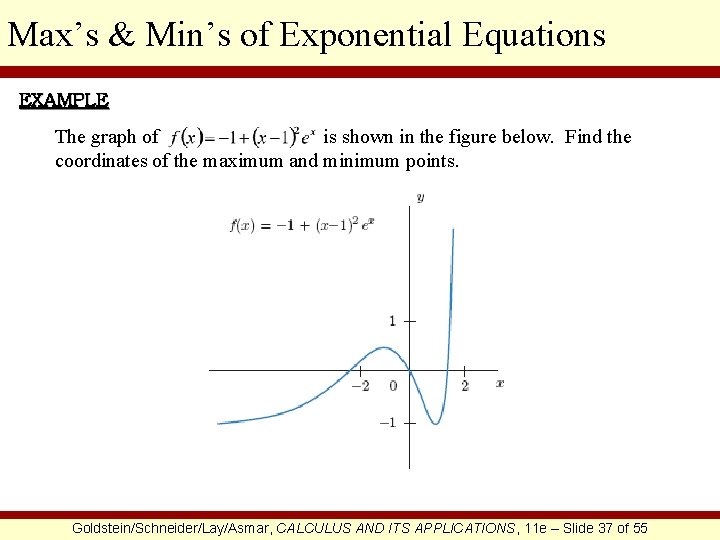
Max’s & Min’s of Exponential Equations EXAMPLE The graph of is shown in the figure below. Find the coordinates of the maximum and minimum points. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 37 of 55

Max’s & Min’s of Exponential Equations CONTINUED At the maximum and minimum points, the graph will have a slope of zero. Therefore, we must determine for what values of x the first derivative is zero. This is the given function. Differentiate using the product rule. Finish differentiating. Factor. Set the derivative equal to 0. Set each factor equal to 0. Simplify. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 38 of 55

Max’s & Min’s of Exponential Equations CONTINUED Therefore, the slope of the function is 0 when x = 1 or x = -1. By looking at the graph, we can see that the relative maximum will occur when x = -1 and that the relative minimum will occur when x = 1. Now we need only determine the corresponding y-coordinates. Therefore, the relative maximum is at (-1, 0. 472) and the relative minimum is at (1, -1). Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 39 of 55

§ 4. 5 The Derivative of ln x Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 40 of 55

Section Outline q Derivatives for Natural Logarithms q Differentiating Logarithmic Expressions Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 41 of 55

Derivative Rules for Natural Logarithms Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 42 of 55

Differentiating Logarithmic Expressions EXAMPLE Differentiate. SOLUTION This is the given expression. Differentiate. Use the power rule. Differentiate ln[g(x)]. Finish. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 43 of 55

Differentiating Logarithmic Expressions EXAMPLE The function has a relative extreme point for x > 0. Find the coordinates of the point. Is it a relative maximum point? SOLUTION This is the given function. Use the quotient rule to differentiate. Simplify. Set the derivative equal to 0. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 44 of 55

Differentiating Logarithmic Expressions CONTINUED The derivative will equal 0 when the numerator equals 0 and the denominator does not equal 0. Set the numerator equal to 0. Write in exponential form. To determine whether the function has a relative maximum at x = 1, let’s use the second derivative. This is the first derivative. Differentiate. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 45 of 55

Differentiating Logarithmic Expressions CONTINUED Simplify. Factor and cancel. Evaluate the second derivative at x = 1. Since the value of the second derivative is negative at x = 1, the function is concave down at x = 1. Therefore, the function does indeed have a relative maximum at x = 1. To find the y-coordinate of this point So, the relative maximum occurs at (1, 1). Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 46 of 55

§ 4. 6 Properties of the Natural Logarithm Function Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 47 of 55

Section Outline q Properties of the Natural Logarithm Function q Simplifying Logarithmic Expressions q Differentiating Logarithmic Expressions q Logarithmic Differentiation Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 48 of 55

Properties of the Natural Logarithm Function Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 49 of 55

Simplifying Logarithmic Expressions EXAMPLE Write as a single logarithm. SOLUTION This is the given expression. Use LIV (this must be done first). Use LIII. Use LI. Simplify. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 50 of 55

Differentiating Logarithmic Expressions EXAMPLE Differentiate. SOLUTION This is the given expression. Rewrite using LIII. Rewrite using LIV. Differentiate. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 51 of 55

Differentiating Logarithmic Expressions CONTINUED Distribute. Finish differentiating. Simplify. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 52 of 55

Logarithmic Differentiation Definition Example Logarithmic Differentiation: Given a function y = f (x), take the natural logarithm of both sides of the equation, Example will follow. use logarithmic rules to break up the right side of the equation into any number of factors, differentiate each factor, and finally solving for the desired derivative. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 53 of 55

Logarithmic Differentiation EXAMPLE Use logarithmic differentiation to differentiate the function. SOLUTION This is the given function. Take the natural logarithm of both sides of the equation. Use LIII. Use LI. Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 54 of 55

Logarithmic Differentiation CONTINUED Use LIV. Differentiate. Solve for f ΄(x). Substitute for f (x). Goldstein/Schneider/Lay/Asmar, CALCULUS AND ITS APPLICATIONS, 11 e – Slide 55 of 55