Chapter 4 The Building Blocks Binary Numbers Boolean

Chapter 4: The Building Blocks: Binary Numbers, Boolean Logic, and Gates Invitation to Computer Science, C++ Version, Third Edition Spring 2005: Additions by S. Steinfadt Invitation to Computer Science, C++ Version, Third Edition

Objectives In this chapter, you will learn about: n The binary numbering system n Boolean logic and gates n Building computer circuits n Control circuits Invitation to Computer Science, C++ Version, Third Edition 2

Introduction n Chapter 4 focuses on hardware design (also called logic design) q q q How to represent and store information inside a computer How to use the principles of symbolic logic to design gates How to use gates to construct circuits that perform operations such as adding and comparing numbers, and fetching instructions Invitation to Computer Science, C++ Version, Third Edition 3

The Binary Numbering System n A computer’s internal storage techniques are different from the way people represent information in daily lives n Information inside a digital computer is stored as a collection of binary data Invitation to Computer Science, C++ Version, Third Edition 4

Binary Representation of Numeric and Textual Information n Binary numbering system q q q Base-2 Built from ones and zeros Each position is a power of 2 1101 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 n Decimal numbering system q q Base-10 Each position is a power of 10 3052 = 3 x 103 + 0 x 102 + 5 x 101 + 2 x 100 Invitation to Computer Science, C++ Version, Third Edition 5

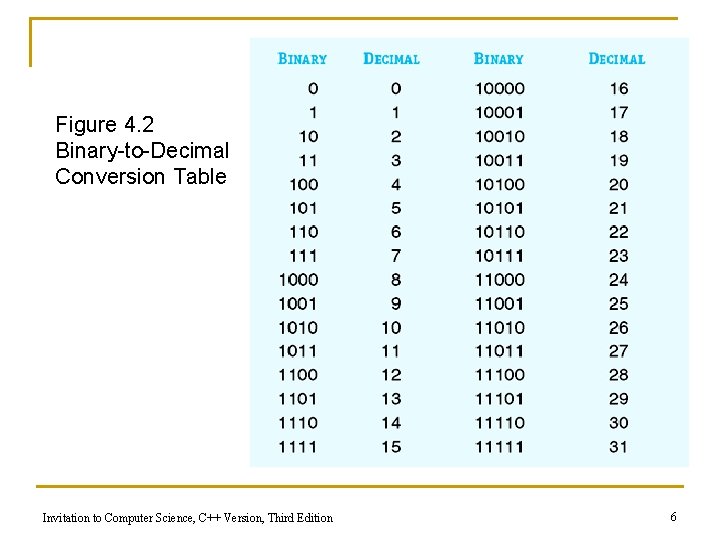
Figure 4. 2 Binary-to-Decimal Conversion Table Invitation to Computer Science, C++ Version, Third Edition 6

Binary Representation of Numeric and Textual Information (continued) n Representing integers q q Decimal integers are converted to binary integers Given k bits, the largest unsigned integer is 2 k - 1 n q Given 4 bits, the largest is 24 -1 = 15 Signed integers must also represent the sign (positive or negative) - Sign/Magnitude notation Invitation to Computer Science, C++ Version, Third Edition 7

Binary Representation of Numeric and Textual Information (continued) n Representing real numbers q Real numbers may be put into binary scientific notation: a x 2 b (or ±M x B±E) n q Number then normalized so that first significant digit is immediately to the right of the binary point n q Example: 101. 11 x 20 Example: . 10111 x 23 Mantissa and exponent then stored Invitation to Computer Science, C++ Version, Third Edition 8

Binary Representation of Numeric and Textual Information (continued) n Characters are mapped onto binary numbers q ASCII code set n q UNICODE code set n n 8 bits per character; 256 character codes 16 bits per character; 65, 536 character codes Text strings are sequences of characters in some encoding Invitation to Computer Science, C++ Version, Third Edition 9

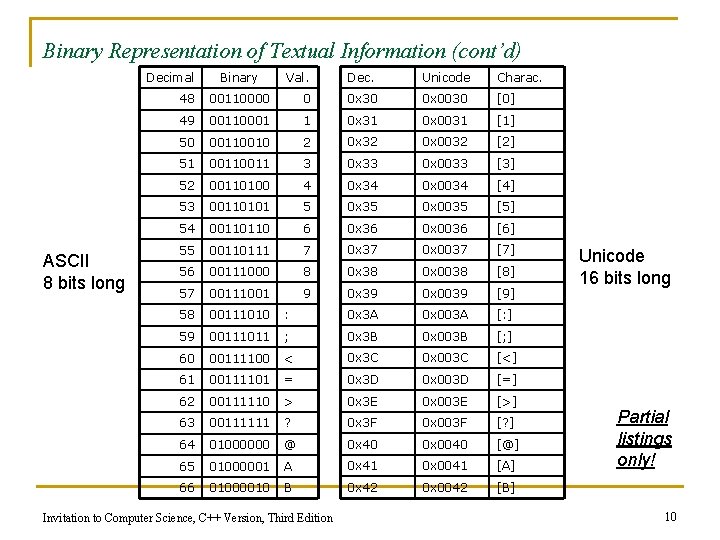
Binary Representation of Textual Information (cont’d) Decimal ASCII 8 bits long Binary Val. Dec. Unicode Charac. 48 00110000 0 0 x 30 0 x 0030 [0] 49 00110001 1 0 x 31 0 x 0031 [1] 50 00110010 2 0 x 32 0 x 0032 [2] 51 0011 3 0 x 33 0 x 0033 [3] 52 00110100 4 0 x 34 0 x 0034 [4] 53 00110101 5 0 x 35 0 x 0035 [5] 54 00110110 6 0 x 36 0 x 0036 [6] 55 00110111 7 0 x 37 0 x 0037 [7] 0 x 0038 [8] 56 00111000 8 0 x 38 57 00111001 9 0 x 39 0 x 0039 [9] 58 00111010 : 0 x 3 A 0 x 003 A [: ] 59 00111011 ; 0 x 3 B 0 x 003 B [; ] 60 00111100 < 0 x 3 C 0 x 003 C [<] 61 00111101 = 0 x 3 D 0 x 003 D [=] 62 00111110 > 0 x 3 E 0 x 003 E [>] 63 00111111 ? 0 x 3 F 0 x 003 F [? ] 64 01000000 @ 0 x 40 0 x 0040 [@] 65 01000001 A 0 x 41 0 x 0041 [A] 66 01000010 B 0 x 42 0 x 0042 [B] Invitation to Computer Science, C++ Version, Third Edition Unicode 16 bits long Partial listings only! 10

Binary Representation of Sound and Images n Multimedia data is sampled to store a digital form, with or without detectable differences n Representing sound data q q Sound data must be digitized for storage in a computer Digitizing means periodic sampling of amplitude values Invitation to Computer Science, C++ Version, Third Edition 11

Binary Representation of Sound and Images (continued) q q From samples, original sound may be approximated To improve the approximation: n Sample more frequently (increase sampling rate) n Use more bits for each sample value ( bit depth) Invitation to Computer Science, C++ Version, Third Edition 12

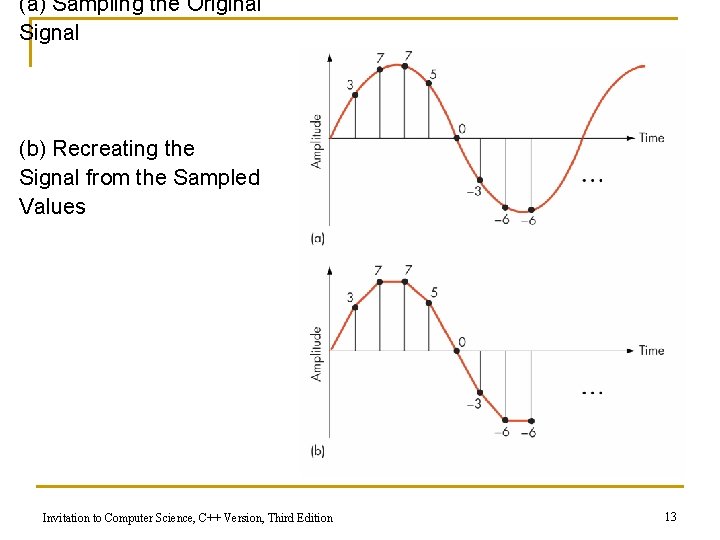
(a) Sampling the Original Signal (b) Recreating the Signal from the Sampled Values Invitation to Computer Science, C++ Version, Third Edition 13

Binary Representation of Sound (cont’d) MP 3 format discussed in text, AAC format here AAC (Advanced Audio Coding) advantages over MP 3 q q q n n Improved compression provides higher-quality results with smaller file sizes Higher resolution audio, yielding sampling rates up to 96 k. Hz Improved decoding efficiency, requiring less processing power for decode http: //www. apple. com/mpeg 4/aac/ http: //www. aac-audio. com/ Invitation to Computer Science, C++ Version, Third Edition 14

Binary Representation of Sound and Images (continued) n Representing image data q q q Images are sampled by reading color and intensity values at even intervals across the image Each sampled point is a pixel Image quality depends on number of bits at each pixel Invitation to Computer Science, C++ Version, Third Edition 15

Binary Representation of Images (cont’d) n Representing image data q q Images are sampled by reading color and intensity values at even intervals across the image Each sampled point is a pixel Image quality depends on number of bits at each pixel More image information: http: //cat. xula. edu/tutorials/imaging/grayscale. php Invitation to Computer Science, C++ Version, Third Edition 16

The Reliability of Binary Representation n Electronic devices are most reliable in a bistable environment n Bistable environment q n Distinguishing only two electronic states n Current flowing or not n Direction of flow Computers are bistable: hence binary representations Invitation to Computer Science, C++ Version, Third Edition 17

Binary Storage Devices n Magnetic core q q q Historic device for computer memory Tiny magnetized rings: flow of current sets the direction of magnetic field Binary values 0 and 1 are represented using the direction of the magnetic field Invitation to Computer Science, C++ Version, Third Edition 18

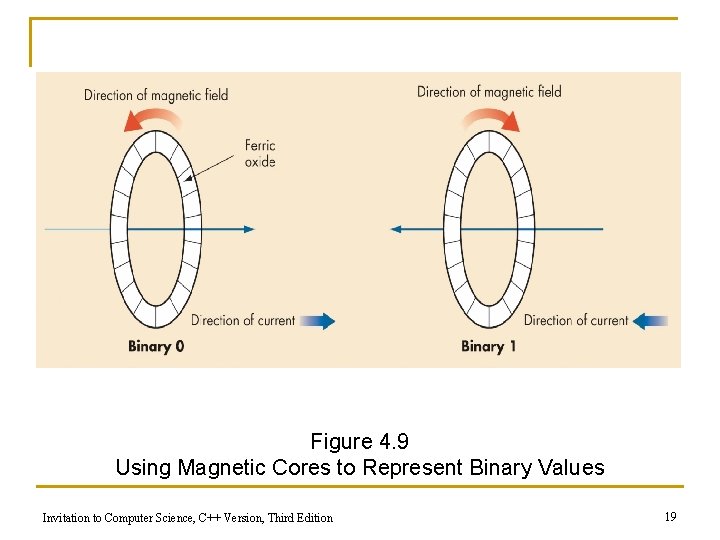
Figure 4. 9 Using Magnetic Cores to Represent Binary Values Invitation to Computer Science, C++ Version, Third Edition 19

Binary Storage Devices (continued) n Transistors q Solid-state switches: either permits or blocks current flow q A control input causes state change q Constructed from semiconductors Invitation to Computer Science, C++ Version, Third Edition 20

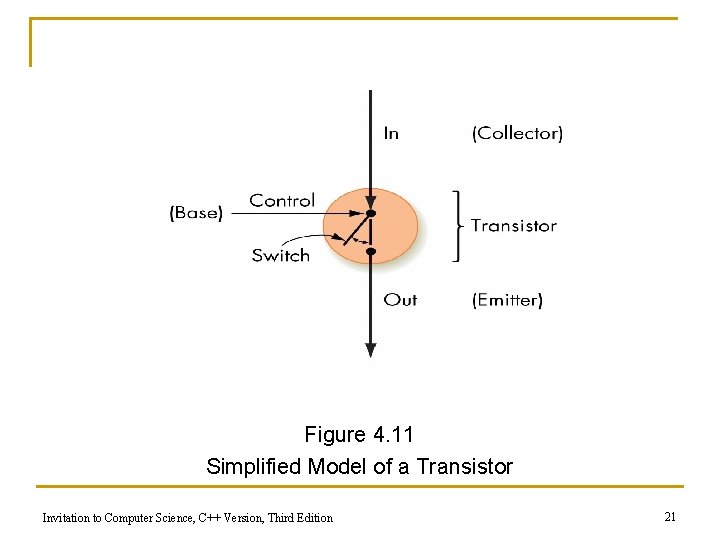
Figure 4. 11 Simplified Model of a Transistor Invitation to Computer Science, C++ Version, Third Edition 21