Chapter 4 Simplex Method for Linear Programming ShiShang

Chapter 4 Simplex Method for Linear Programming Shi-Shang Jang Chemical Engineering Department National Tsing-Hua University

Example 1: Inspector Problem l Assume that it is desired to hire some inspectors for monitoring a production line. A total amount of 1800 species of products are manufactured every day (8 working hours), while two grades of inspectors can be found. Maximum, 8 grade A inspector and 10 grade B inspector are available from the job market. Grade A inspectors can check 25 species/hour, with an accuracy of 98 percent. Grade B inspectors can check 15 species/hour, with an accuracy of 95 percent. Note that each error costs $2. 00/piece. The wage of a grade A inspector is $4. 00/hour, and the wage of a grade B inspector is $3. 00/hour. What is the optimum policy for hiring the inspectors?

Problem Formulation Assume that the x 1 grade A inspectors x 2 grade B inspects are hired, then l total cost to be minimized l 4 8 x 1 +3 8 x 2 +25 8 0. 02 2 x 1 +15 8 0. 05 2 x 2 =40 x 1 +36 x 2 l manufacturing constraint l 25 8 x 1 +15 8 x 2 1, 800 200 x 1 +120 x 2 1, 800 l no. of inspectors available: l 0 x 1 8 l 0 x 2 10 l

The Graphical Solution

Theorem l Property: If there exists an optimal solution to a LP, then at least one of the corner point of the feasible region will always qualify to be an optimal solution.

Special Cases l l l Alternate Solutions (non-unique solutions) Max x 1+2 x 2 s. t. x 1+2 x 2 10 x 1+ x 2 1 x 2 4 x 1 0, x 2 0

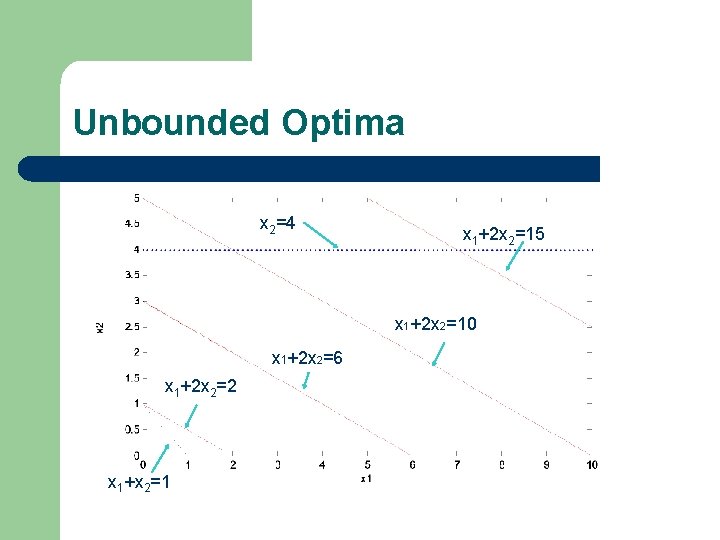
Special Cases - continued l l Unbounded Optima : A system has a feasible region with open boundaries such that the optima may appear at the infinity. Example: For the previous example, in case the constraint x 1+2 x 2 10 is not given, then moving far away from the origin increases the objective function x 1+2 x 2, and the maxim Z would be +

Unbounded Optima x 2=4 x 1+2 x 2=15 x 1+2 x 2=10 x 1+2 x 2=6 x 1+2 x 2=2 x 1+x 2=1

Example 2: Student Fab l l The RIT student-run microelectronic fabrication facility is taking orders for four indigenously developed ASIC chips that can be used in (1) touch sensors ($6, s 4 hr, m 1 hr, v 30), (2)LCD($10, s 9 hr, m 1 hr, v 40), (3) pressure sensors($9, s 7 hr, m 3 hr, v 20), and (4) controllers($20, s 10 hr, m 8 hr, v 10). Constraints : Student hr≦ 600, machine hr≦ 420, space≦ 800

The LP Problem

4 -2 The Basic Approach l Standard Form of Linear Programming

Handling of in-equality Constraints Case 1: Slack Variable: x 1+2 x 2+3 x 3 +4 x 4 25 l – Modified to x 1+2 x 2+3 x 3+4 x 4+ x 5=25 x 5 0 is a slack variable. Case 2: Surplus Variable: 2 x 1+ x 2 -3 x 3 12 l Modified to 2 x 1+ x 2 -3 x 3 - x 4=12 x 4 0 is a surplus variable. –

Handling of Equality Constraints l l l If s is unrestricted, i. e. , s can be positive or negative, then we set s=s+-ssuch that s+ 0, s- 0.

Example Modify to

Definitions l l l Definition: A feasible region, denoted by S is the set of all feasible solution. Mathematically, . Definition: An optimal solution is a vector x* S, s. t. z 0=c. Tx* is maximum or minimum in where Z is termed by the optimal value. Definition: Alternate optimal solution is a set X S, s. t. all x X has the same objective value z 0 and for all x S, and z=c. Tx, z z 0. Definition: If the solution set of LP contains only one element, it is termed the unique optimum. Definition: If the optimum value z approaches to infinity, then the LP is said to have unbounded optimum.

4 -3 The Simplex Method

Definitions l l Definition: A pivot operation is sequence of elementary row operations that reduce the coefficients of a specified variable to unity in one of the equation and zero elsewhere. Definition: In the above canonical form, x 1, , xm are termed the basic variables or dependent variables, xm+1, , xn are called nonbasic variables or the independent variables. Definition: The solution obtained from a canonical form is by setting the nonbasic variable or independent variable to zero is called a basic solution. Definition: A basic feasible solution is a basic solution in which the basic or dependent variables are non-negative.

Property Remark: where Definition: Property: A feasible basic solution is a simplex of the feasible region. Note: Given a canonical form and feasible basic solution, then the objective function: where x. B is a basic variable.

Approach (Simplex Method): l l l Start with an initial basic feasible solution in canonical form. Improve the solution by finding another basic feasible solution if possible. When a particular basic feasible solution is found, and cannot be improved by finding new basic feasible solution, the optimality is reached. l l Definition: An adjacent basic solution differs from a basic solution is exactly one basic variable. Question: If one wants to find an adjacent feasible basic solution from one feasible basic solution (i. e. , switch to another simplex), which adjacent basic solution gives lowest objective function?

Derivation of Inner Product Rule Supposing, one wants to replace one of the original basic variable with nonbasic variable xs, we firstly, increase xs from zero to one, then for all i=1, , m, and, for all j=m+1, , n, j s. xj=0

Theorem 1 (Inner Product Rule) Relative cost, (inner product rule) More: (1) In a minimization problem, a basic feasible solution is optimal if the relative costs of its all nonbasic variable are all positive or zero. (2) One should choose an adjacent basic solution from which the relative cost is the minimum. Corollary: The alternate optima exists if z=0.

Theorem 2: (The Minimum Ratio Rule ) l Given a nonbasic variable xs is change into the basic variable set, then one of the basic variable xr should leave from the basic variable set, such that: The above minimum happens at i=r. Corollary: The above rule fails if there exist unbounded optima.

Example: The LP Problem

The Standard Form

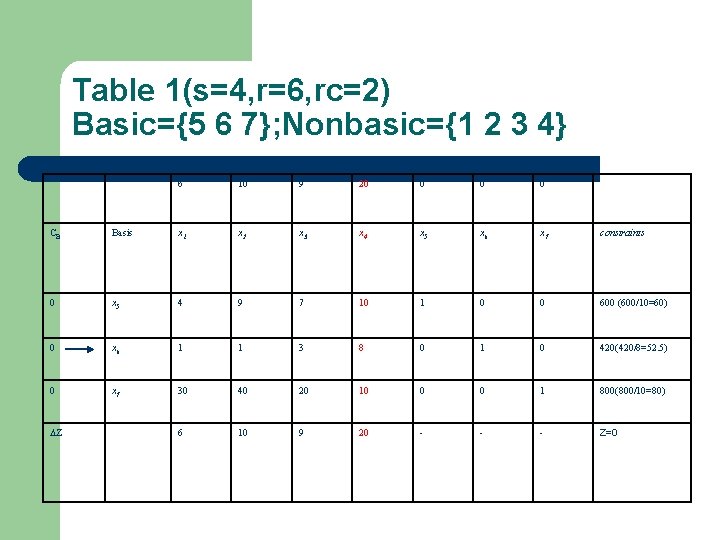
Table 1(s=4, r=6, rc=2) Basic={5 6 7}; Nonbasic={1 2 3 4} 　 6 10 9 20 0 CB Basis x 1 x 2 x 3 x 4 x 5 x 6 x 7 constraints 0 x 5 4 9 7 10 1 0 0 600 (600/10=60) 0 x 6 1 1 3 8 0 1 0 420(420/8=52. 5) 0 x 7 30 40 20 10 0 0 1 800(800/10=80) 6 10 9 20 - - - Z=0 Z

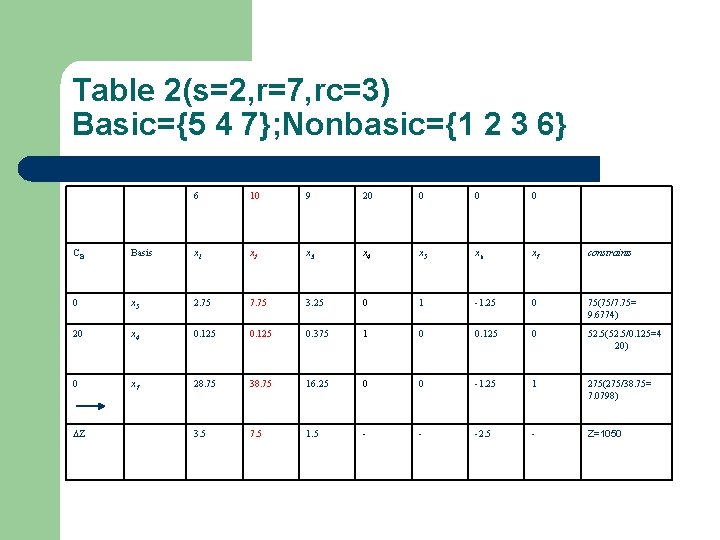
Table 2(s=2, r=7, rc=3) Basic={5 4 7}; Nonbasic={1 2 3 6} 　 6 10 9 20 0 CB Basis x 1 x 2 x 3 x 4 x 5 x 6 x 7 constraints 0 x 5 2. 75 7. 75 3. 25 0 1 -1. 25 0 75(75/7. 75= 9. 6774) 20 x 4 0. 125 0. 375 1 0 0. 125 0 52. 5(52. 5/0. 125=4 20) 0 x 7 28. 75 38. 75 16. 25 0 0 -1. 25 1 275(275/38. 75= 7. 0798) 3. 5 7. 5 1. 5 - - -2. 5 - Z=1050 Z

Table 3 Basic={5 4 2}; Nonbasic={1 7 3 6} 　 6 10 9 20 0 CB Basis x 1 x 2 x 3 x 4 x 5 x 6 x 7 constraints 0 x 5 -3 0 0 0 1 -1 -0. 2 20 20 x 4 0. 0323 0 0. 3226 1 0 0. 129 -0. 0032 51. 6129 10 x 2 0. 7419 1 0. 4194 0 0 -0. 0323 0. 0258 7. 0968 -2. 0645 - -0. 1935 - - -1. 6452 -2. 2581 Z=1103. 226 Z

2. The Two Phase Simplex Method. Example

The Standard Form

Two Phase Approach-Phase I

Two Phase Approach-Phase I Table 1 　 0 0 0 1 1 CB Basis x 1 x 2 x 3 x 4 x 5 x 6 x 7 constraints 0 x 4 1 -2 1 1 0 0 0 11(11/1=11) 1 x 6 -4 1 2 0 -1 1 0 3(3/2=1. 5) 1 x 7 -2 0 1 0 0 0 1 1(1/1=1) Z 6 -1 -3 - 1 - - Z=4

Two Phase Approach-Phase I Final 　 0 0 0 1 1 CB Basis x 1 x 2 x 3 x 4 x 5 x 6 x 7 constraints 0 x 4 3 0 0 1 -2 2 -5 12 0 x 2 0 1 0 0 -1 1 -2 1 0 x 3 -2 0 1 0 0 0 -1 1 Z - - - - Z=0

Two Phase Approach-Phase II Table 1 　 -3 1 1 0 0 CB Basis x 1 x 2 x 3 x 4 x 5 constraints 0 x 4 3 0 0 1 -2 12(12/3=4) 1 x 2 0 1 0 0 -1 1(1/0= ) 1 x 3 -2 0 1 0 0 1(1/-2<0) Z -1 - - - 5 Z=2

Two Phase Approach-Phase II Final 　 -3 1 1 0 0 CB Basis x 1 x 2 x 3 x 4 x 5 constraints -3 x 1 1 0 0 0. 3333 -0. 667 4 1 x 2 0 1 0 0 -1 1 1 x 3 0 0 1 0. 6667 -1. 333 9 Z - - - Z=-2

Example: Multi-Products Manufacturing l A company manufactures three products: A, B, and C. Each unit of product A requires 1 hr of engineering service, 10 hr of direct labor, and 3 lb of material. To produce one unit of product B requires 2 hr of engineering, 4 hr of direct labor, and 2 lb of material. In case of product C, it requires 1 hr of engineering, 5 hr of direct labor, and 1 lb of material. There are 100 hr of engineering, 700 hr of labor, and 400 lb of material available. Since the company offers discounts for bulk purchases, the profit figures are as shown in the next slide:

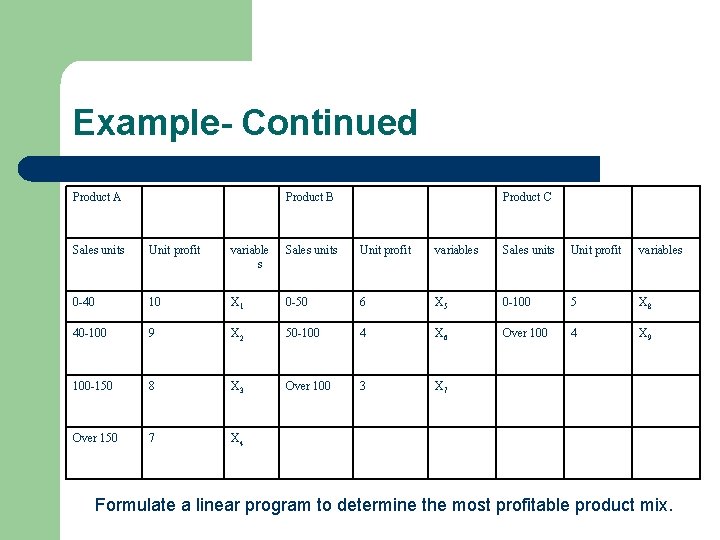
Example- Continued Product A Product B Product C Sales units Unit profit variable s Sales units Unit profit variables 0 -40 10 X 1 0 -50 6 X 5 0 -100 5 X 8 40 -100 9 X 2 50 -100 4 X 6 Over 100 4 X 9 100 -150 8 X 3 Over 100 3 X 7 Over 150 7 X 4 Formulate a linear program to determine the most profitable product mix.

Problem Formulation Let’s denote the variables as shown in the table, then we have the following:

MATLAB PROGRAM l l l l f=[-10 -9 -8 -7 -6 -4 -3 -5 -4]'; A=[1 1 2 2 2 1 1; 10 10 4 4 4 5 5; 3 3 2 2 2 1 1]; b=[100; 700; 400]; Aeq=[]; beq=[]; LB=[0 0 0 0 0]; UB=[40 60 50 Inf 50 50 Inf 100 Inf]; [X, FVAL, EXITFLAG, OUTPUT, LAMBDA]=LINPROG( f, A, b, Aeq, beq, LB, UB)

Solution l X’= 40. 0000 22. 5000 0. 0000 18. 7500 0. 0000 l FVAL =-715. 0000 EXITFLAG =1 OUTPUT = iterations: 7 cgiterations: 0 algorithm: 'lipsol' LAMBDA = ineqlin: [3 x 1 double] eqlin: [0 x 1 double] upper: [9 x 1 double] lower: [9 x 1 double] l l l l l

3. Sensitivity Analysis l l l Shadow Prices: To evaluate net impact in the maximum profit if additional units of certain resources can be obtained. Opportunity Costs: To measure the negative impact of producing some products that are zero at the optimum. The range on the objective function coefficients and the range on the RHS row.

Example l A factory manufactures three products, which require three resources – labor, materials and administration. The unit profits on these products are $10, $6 and $4 respectively. There are 100 hr of labor, 600 lb of material, and 300 hr of administration available per day. In order to determine the optimal product mix, the following LP model is formulated and solve:

Basic LP Problem

Optimal Solution and Sensitivity Analysis x 1=33. 33, x 2=66. 67, x 3=0, Z=733. 33 l Shadow prices for row 1=3. 33, row 2=0. 67, row 3=0 l Opportunity Costs for x 3=2. 67 l Ranges on the objective function coefficients: 6≦c 1(10)≦ 15, 4≦c 2(6)≦ 10, -∞≦c 3(4)≦ 6. 67 l

Optimal Solution and Sensitivity Analysis- Continued 60≦b 1(100)≦ 150, 400≦b 2(600)≦ 1000, 200≦b 3(300)≦∞ l

100% Rules l 100% rule for objective function coefficients l 100% rule for RHS constants

Examples l Unit profit on product 1 decrease by $1, but increases by $1 for products 2 and 3, will the optimum change? (δc 1=-1, Δc 1=4, δc 2=1, Δc 2=4, δc 3=1, Δc 3=2. 67) l Simultaneous variation of 10 hr decrease on labor 100 lb increase in material and 50 hr decrease on administration