Chapter 4 ScanConverting a LINE Simple DDA Digital

Chapter 4 元素 Scan-Converting a LINE 畫出顯示一條線 Simple DDA Digital Differential Analyzer (x 2, y 2) (x 1, y 1) 1

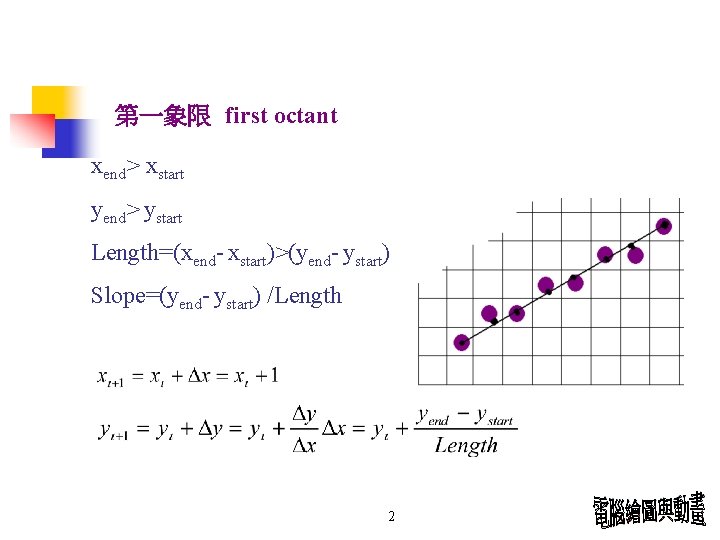
第一象限 first octant xend> xstart yend> ystart Length=(xend- xstart)>(yend- ystart) Slope=(yend- ystart) /Length 2

Simple DDA Digital Differential Analyzer (x 2, y 2) (x 1, y 1) 3

Left to Right (Left to Right) 4

Right to Left ( Right to Left) x 1 x 2 ( Right to Left) y 1 y 2 5

Simple DDA (x 2, y 2) (x 1, y 1) +m 6

Simple DDA (x 2, y 2) (x 1, y 1) -m 7

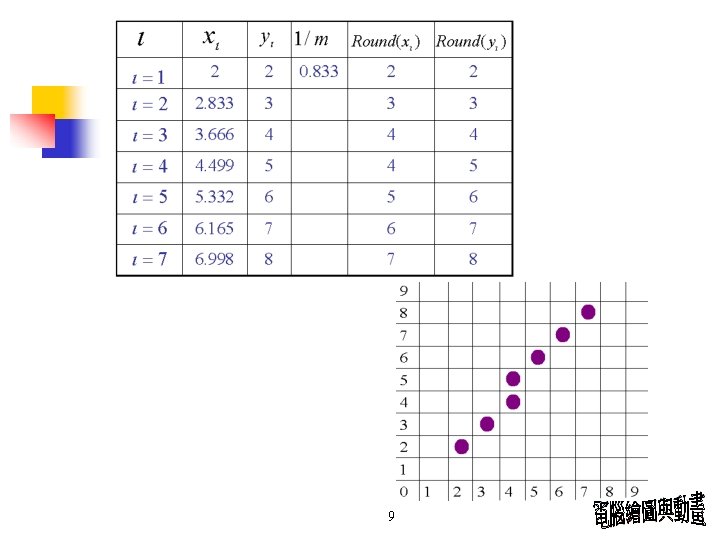
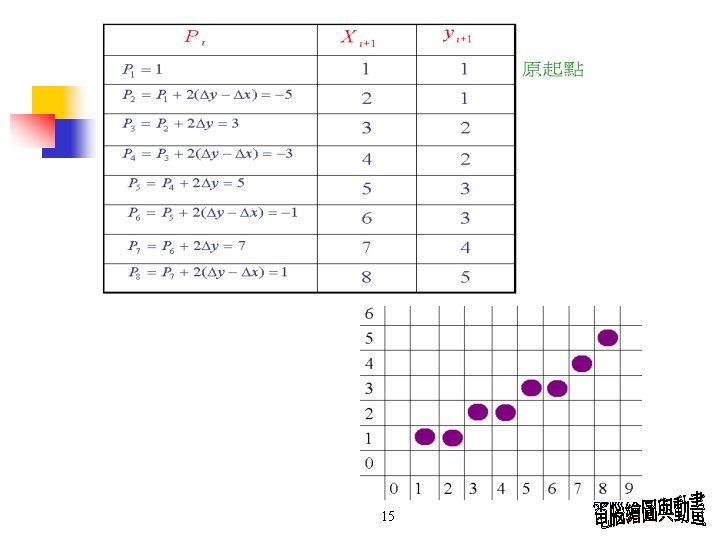
Simple DDA Example : From (2, 2) to (7, 8) (x 1, y 1) (x 2, y 2) , (7, 8) (2, 2) 8

9

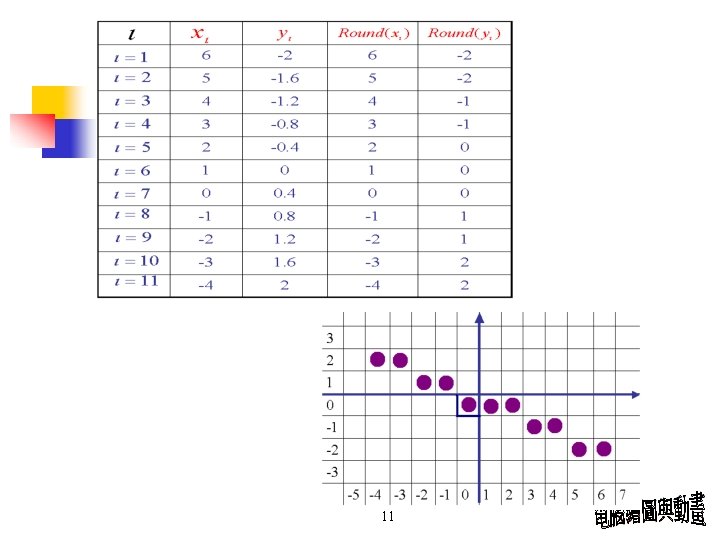
Simple DDA Example From (6, -2) to (-4, 2) (x 1, y 1) (x 2, y 2) 10

11

Bresenham’s Line Algorithm 1. Left end point (x 1, y 1) Right end point (x 2, y 2) 2. First point (x 1, y 1) 12

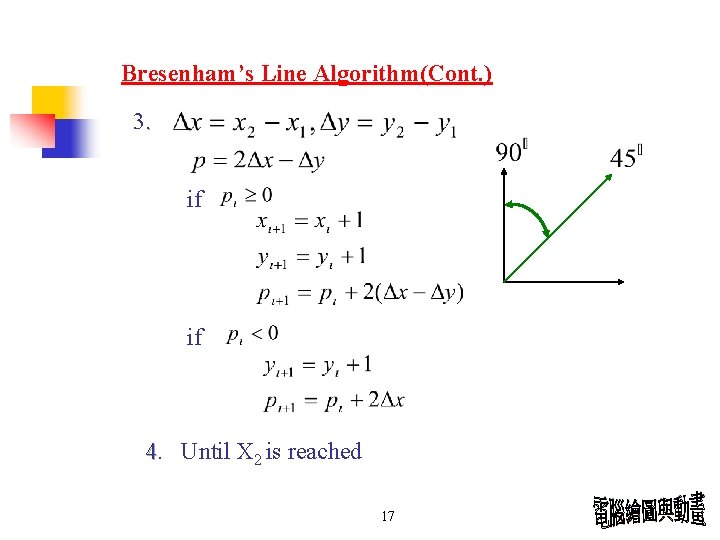
Bresenham’s Line Algorithm(Cont. ) 3. if if 4. Until X 2 is reached 13

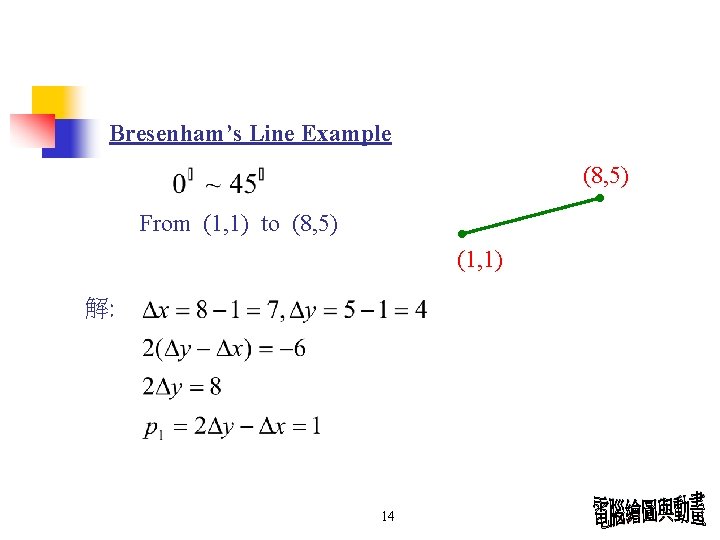
Bresenham’s Line Example (8, 5) From (1, 1) to (8, 5) (1, 1) 解: 14

15

Bresenham’s Line Algorithm 1. Left end point (x 1, y 1) Right end point (x 2, y 2) 2. First point (x 1, y 1) 16

Bresenham’s Line Algorithm(Cont. ) 3. if if 4. Until X 2 is reached 17

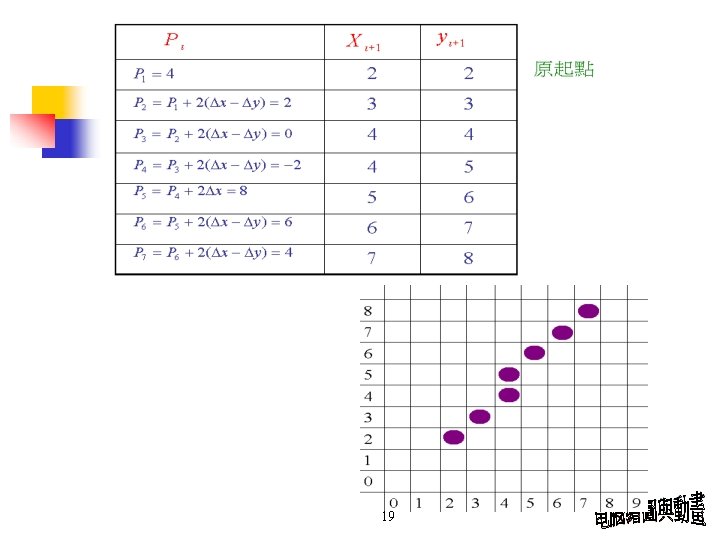
Bresenham’s Line Example (7, 8) From (2, 2) to (7, 8) (2, 2) 解: 18

19

Quadrantal DDA 4 個象限的DDA Use line error (tracking sum) No float point calculation 4 Quadrant 象限 Ⅱ Ⅰ Ⅲ Ⅳ 開始 e=0 20

4 Quadrant 象限 ⅡⅠ Ⅰ Ⅱ Ⅲ Ⅳ Quadrant 1 Rules 1. if error <0, move +x , add 2. if error 0, move +y , add Quadrant 2 Rules 1. if error <0, move –x , add 2. if error 0, move +y , add Quadrant 3 Rules 1. if error <0, move –x , add 2. if error 0, move –y , add Quadrant 4 Rules 1. if error <0, move +x , add 2. if error 0, move –y , add 21 ⅢⅣ to error to error

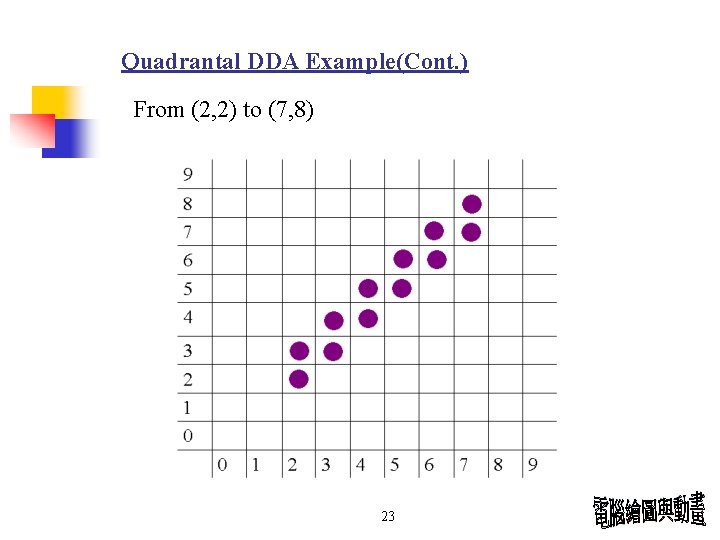
Quadrantal DDA Example x 2>x 1 I{ y >y 2 1 From (2, 2) to (7, 8) 開始 e=0 22

Quadrantal DDA Example(Cont. ) From (2, 2) to (7, 8) 23

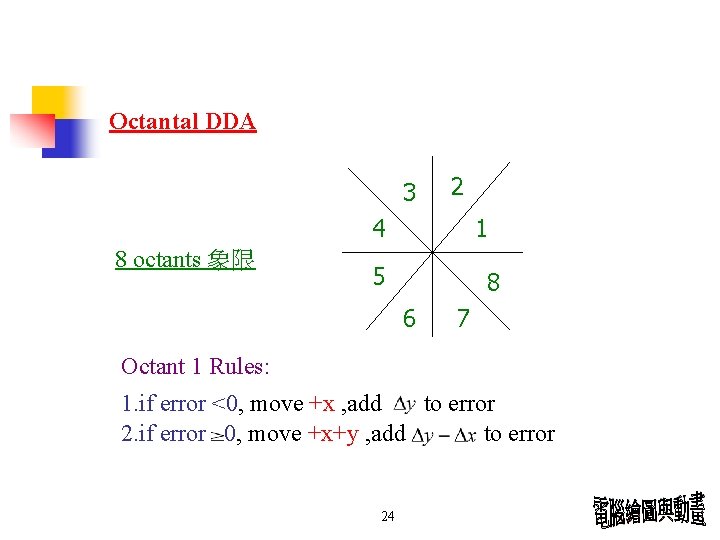
Octantal DDA 3 2 4 8 octants 象限 1 5 8 6 7 Octant 1 Rules: 1. if error <0, move +x , add to error 2. if error 0, move +x+y , add to error 24

3 2 Octant 2 Rules: 6 1. if error <0, move +x+y , add to error 2. if error 0, move +y , add to error 7 4 8 octants 象限 5 Octant 3, 4, 5, 6 Rules: Swap start point and End point , Draw as 1, 2, 7, 8 Octant 7 Rules: 1. if error <0, move +x-y , add to error 2. if error 0, move –y , add to error Octant 8 Rules : 1. if error <0, move +x , add to error 2. if error > 0, move +x–y , add to error 25 1 8

Octantal DDA Example From (2, 2) to (7, 8) 2 Octant 2 Ⅱ 26

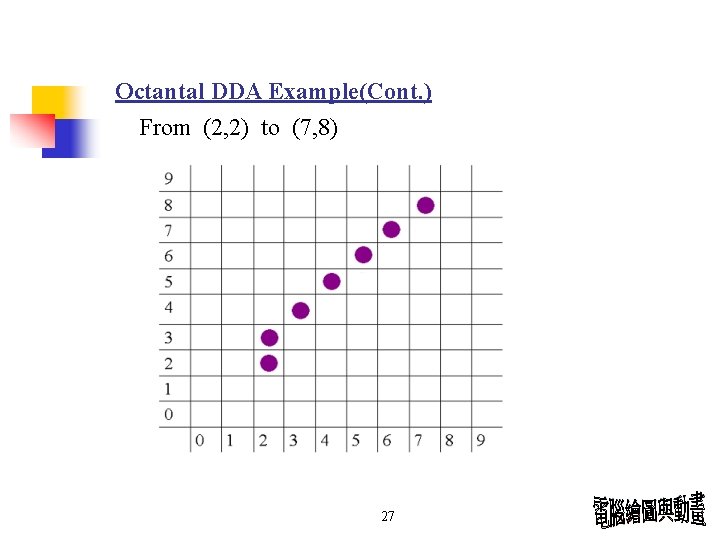
Octantal DDA Example(Cont. ) From (2, 2) to (7, 8) 27

Scan-Converting a Circle y Pythagoream Theorem x Stepping along x axis Unit steps from x = (xc-r) to x = (xc+r) Calculate y Not Uniform 28

Parametric Polar r fixed step angular value step size 1/r 29

Bresenham’s Circle Algorithm 1. first point (x 1 , y 1)=(0 , r) 2. P 1= 3 -2 r if P 1<0, If P 1 0, 3. Plot 8 points (x, y), (-x, y) , (x, -y) , (-x, -y) , (y, x) , (-y, x) , (y, -x) , (-y, -x) 4. Until x y 30

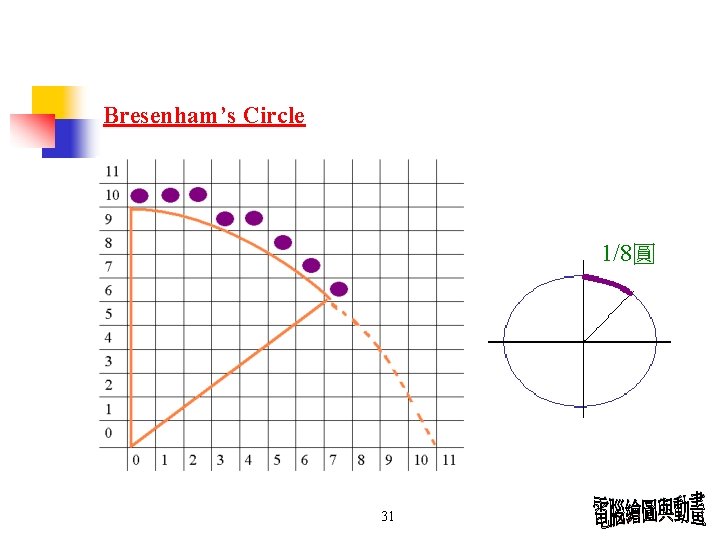
Bresenham’s Circle 1/8圓 31

r =10 , (0 , 0) 圓心 , P 1 =3 -2 r p P 0 x 0 y r =10 P 1 = 3 -2 r=-17 P 2 = -17+4+6=-7 1 2 10 10 P 3 = -7+8+6=7 P 4 = 7+4(-6)+10=7 P 5 =-7+4(4)+10=15 P 6 = 15+(-12)+10=13 P 7 = 13+(-4)+10=19 3 4 5 6 7 9 9 8 7 6 , 32

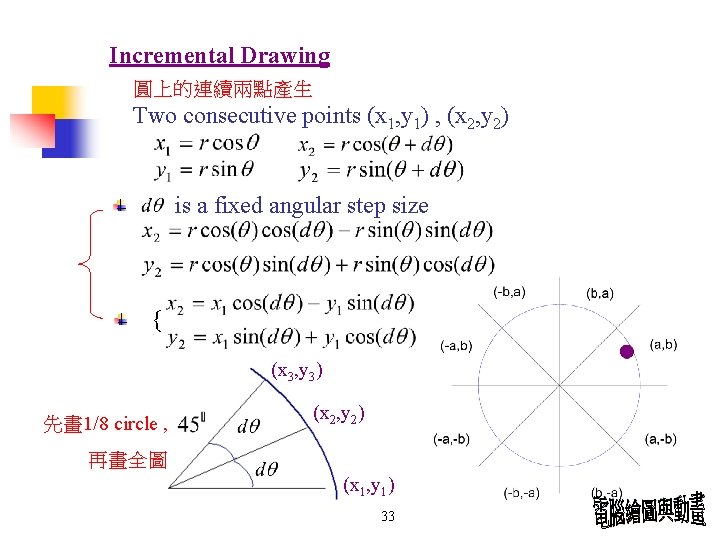
Incremental Drawing 圓上的連續兩點產生 Two consecutive points (x 1, y 1) , (x 2, y 2) is a fixed angular step size { (x 3, y 3) 先畫 1/8 circle , (x 2, y 2) 再畫全圖 (x 1, y 1) 33

Mid point Circle Algorithm Input r , (xc, yc) 1. First point (x 0, y 0)=(0 , r) 2. 3. k =0, … If , Next point (xk+1, yk) Otherwise , Next point (xk+1, yk-1) 4. 決定其他對稱象限 5. 圓心 6. 直到 34

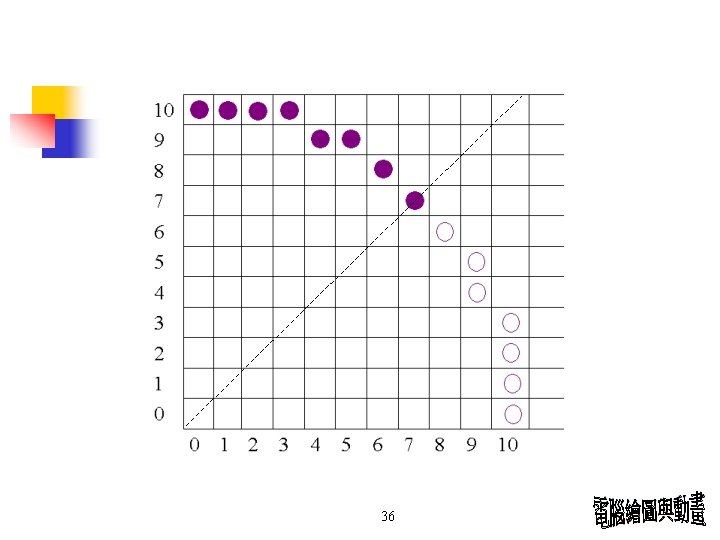
例: r =10 第一象限 from x = 0 to x = y P 0=1 -r = -9 (x 0, y 0)=(0, 10) 2 x 0 =0 , 2 y 0=20 35

36