Chapter 4 Queue Example Outline n n Concept

Chapter 4: Queue (队列)

Example

Outline n n Concept Implementation of Queue Class Applications

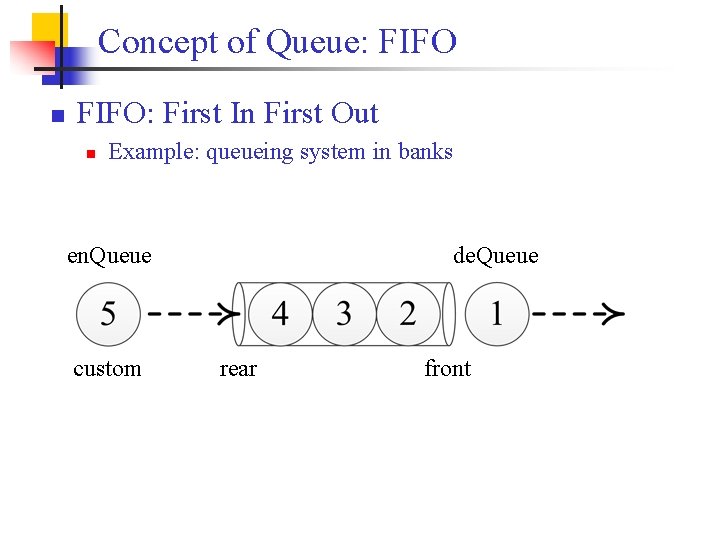
Concept of Queue: FIFO n FIFO: First In First Out n Example: queueing system in banks en. Queue custom de. Queue rear front

Operation: create() n Create an empty queue

Operation: en. Queue(x) (入队) n Inset x to the rear of the queue

Operation: x = de. Queue() (出队) n Delete the head node and return its value x=1

Operation: x = get. Head() n Return the value of the head node x=2

Operation: is. Empty() n If the queue is empty: return yes otherwise, return no yes no

Outline n n Concept Implementation of Queue n n Implementation by sequence list Implementation by linked list Implementation of Queue Class Applications

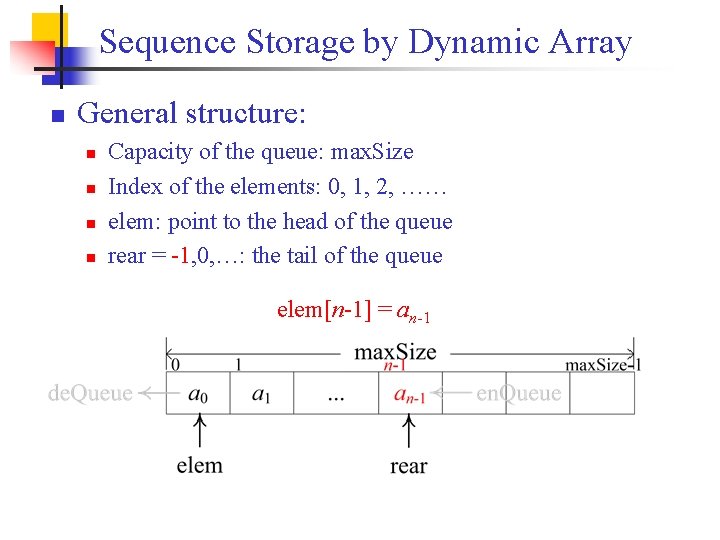
Sequence Storage by Dynamic Array n General structure: n n Capacity of the queue: max. Size Index of the elements: 0, 1, 2, …… elem: point to the head of the queue rear = -1, 0, …: the tail of the queue elem[n-1] = an-1

Fixed Front n n When the queue is empty, rear = -1 Index of the front is fixed at 0 Empty queue

Fixed Front: en. Queue n Index of the front is fixed at 0 Before en. Queue an+1 After en. Queue an+1

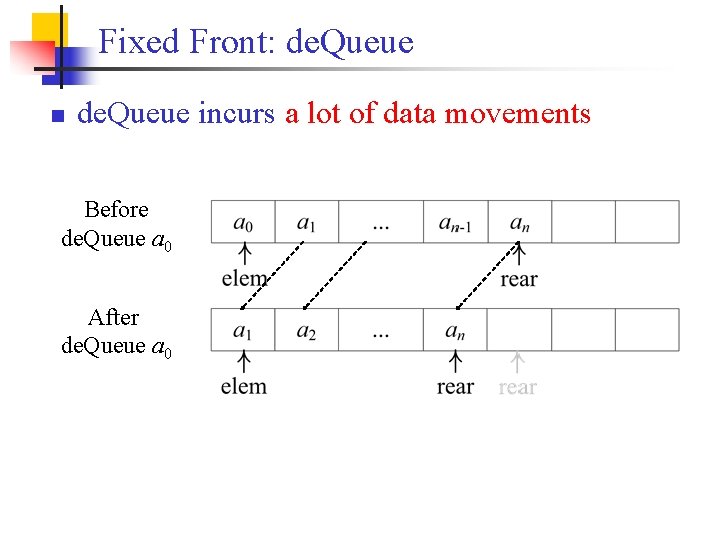
Fixed Front: de. Queue n de. Queue incurs a lot of data movements Before de. Queue a 0 After de. Queue a 0

Unfixed Front n front = -1, 0, 1, …: the address before the head n n front is introduced for de. Queue() rear: point to the end n n Empty queue: front = rear = -1 Full queue: rear = max. Size - 1 Empty Queue Full Queue

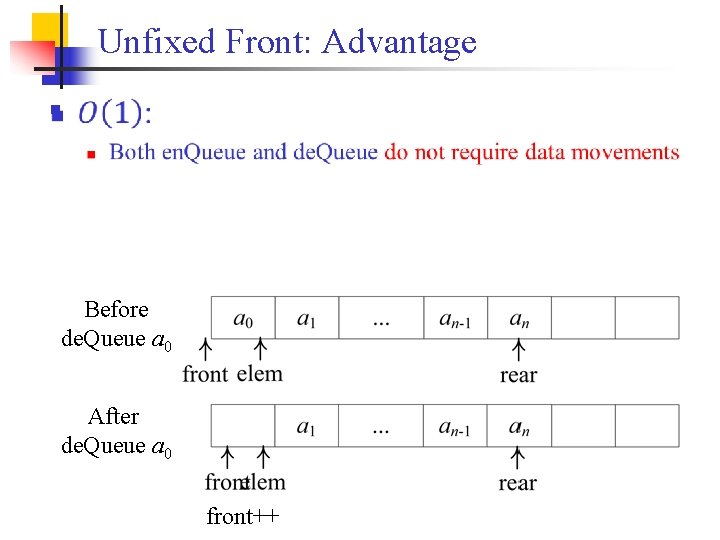
Unfixed Front: Advantage n Before de. Queue a 0 After de. Queue a 0 front++

Unfixed Front: Disadvantage n Low memory utilization n Nodes before the front can not be utilized any more Before de. Queue a 0 ~ an-1 After de. Queue a 0~ an-1 & en. Queue an+1, an+2 can not be utilized

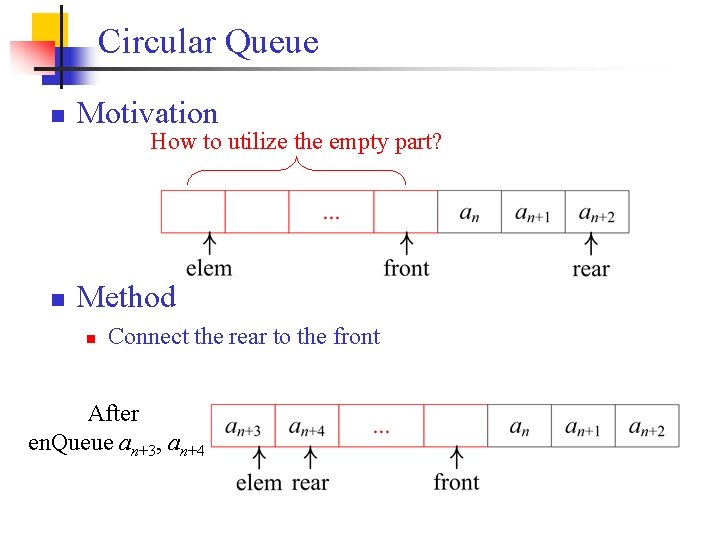
Circular Queue n Motivation How to utilize the empty part? n Method n Connect the rear to the front After en. Queue an+3, an+4

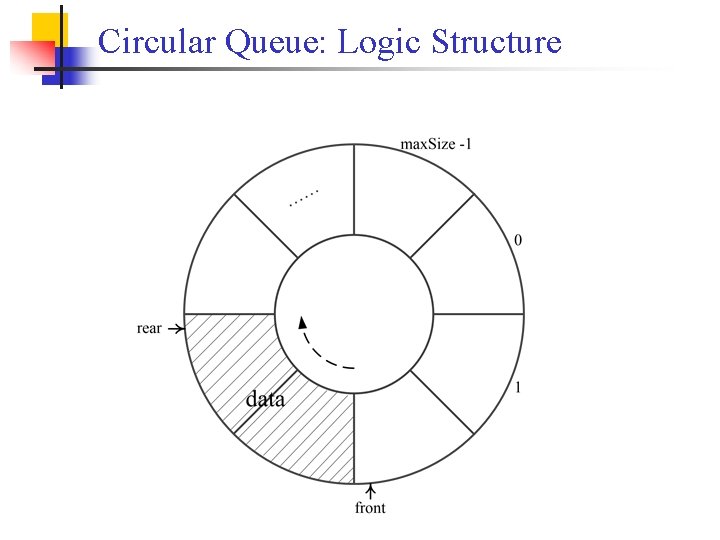
Circular Queue: Logic Structure

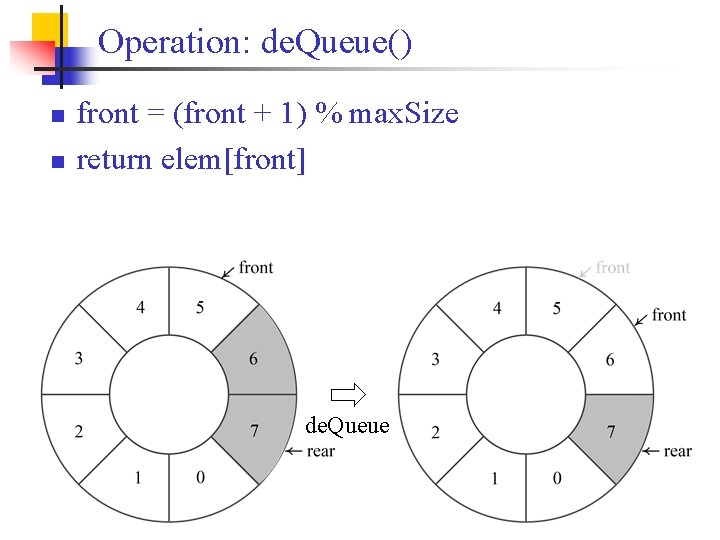
How to de. Queue? n n n front = (front + 1) % max. Size return elem[front] Example: max. Size = 7 front = 6 Before de. Queue A After de. Queue A front = (front+1)%7 = (6+1)%7 = 0 return elem[0]

How to en. Queue? n n n rear = (rear + 1) % max. Size elem[rear] = x Example: max. Size = 7 rear = 6 Before enqueue of H After enqueue of H rear = (rear+1)%7 = (6+1)%7 = 0 elem[0] = H

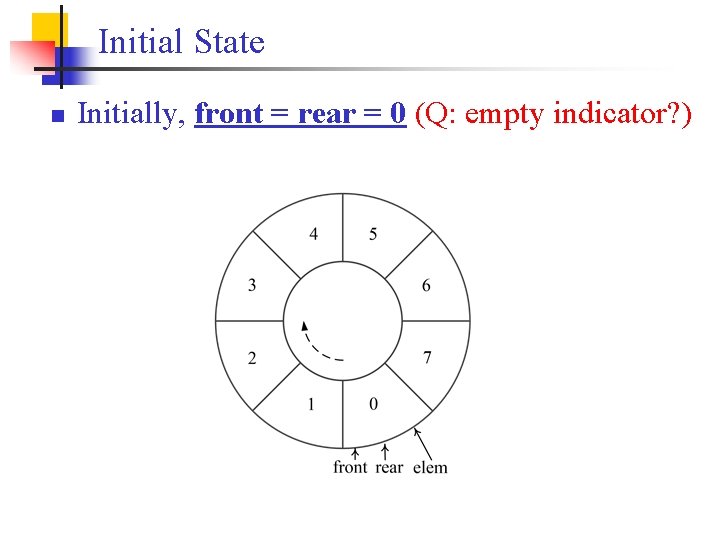
Initial State n Initially, front = rear = 0 (Q: empty indicator? )

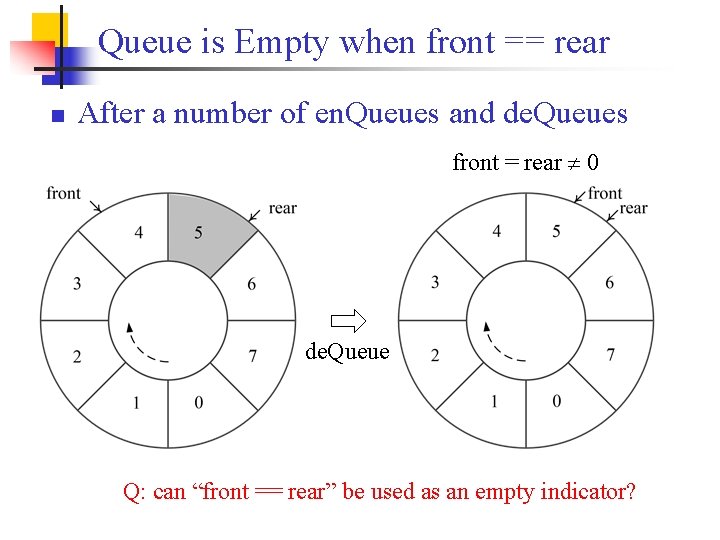
Queue is Empty when front == rear n After a number of en. Queues and de. Queues front = rear 0 de. Queue Q: can “front == rear” be used as an empty indicator?

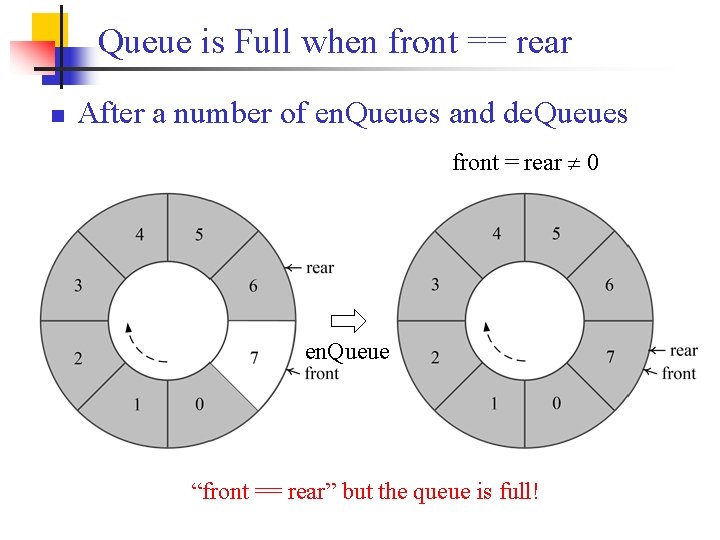
Queue is Full when front == rear n After a number of en. Queues and de. Queues front = rear 0 en. Queue “front == rear” but the queue is full!

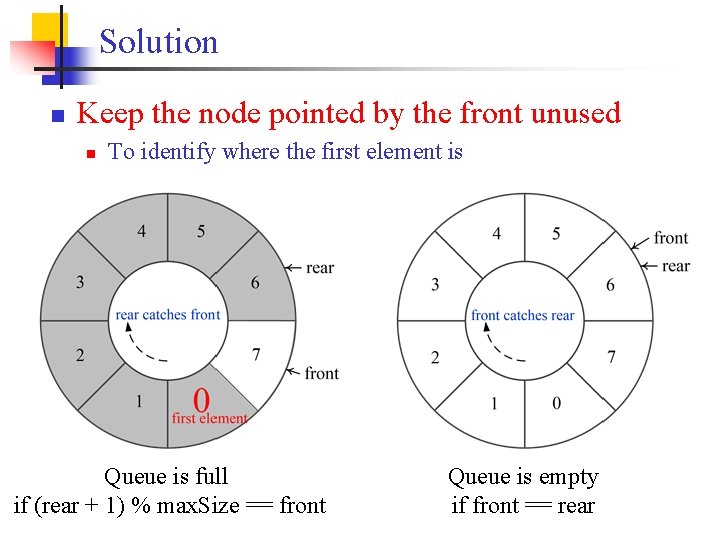
Solution n Keep the node pointed by the front unused n To identify where the first element is Queue is full if (rear + 1) % max. Size == front Queue is empty if front == rear

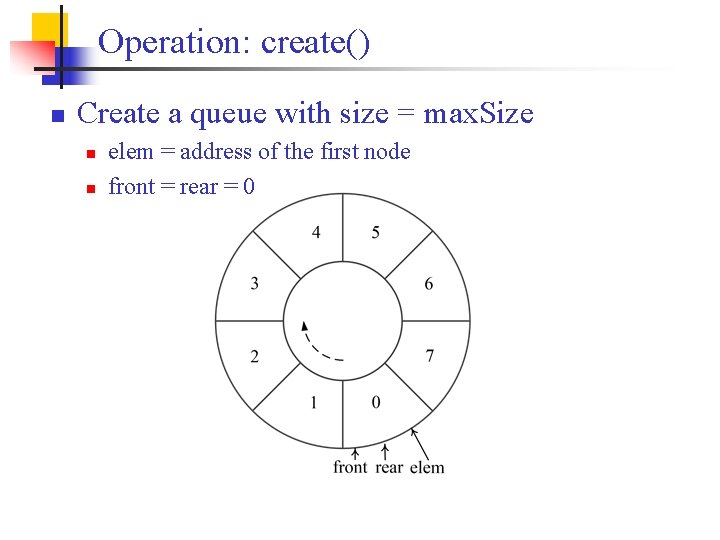
Operation: create() n Create a queue with size = max. Size n n elem = address of the first node front = rear = 0

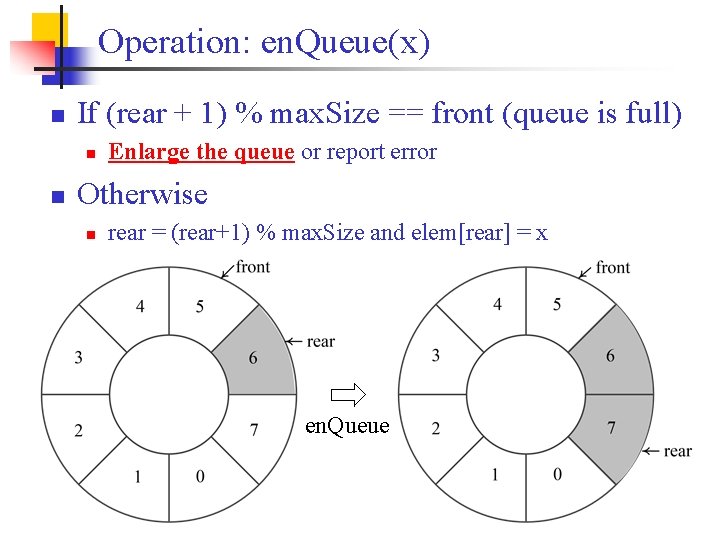
Operation: en. Queue(x) n If (rear + 1) % max. Size == front (queue is full) n n Enlarge the queue or report error Otherwise n rear = (rear+1) % max. Size and elem[rear] = x en. Queue

Operation: de. Queue() n n front = (front + 1) % max. Size return elem[front] de. Queue

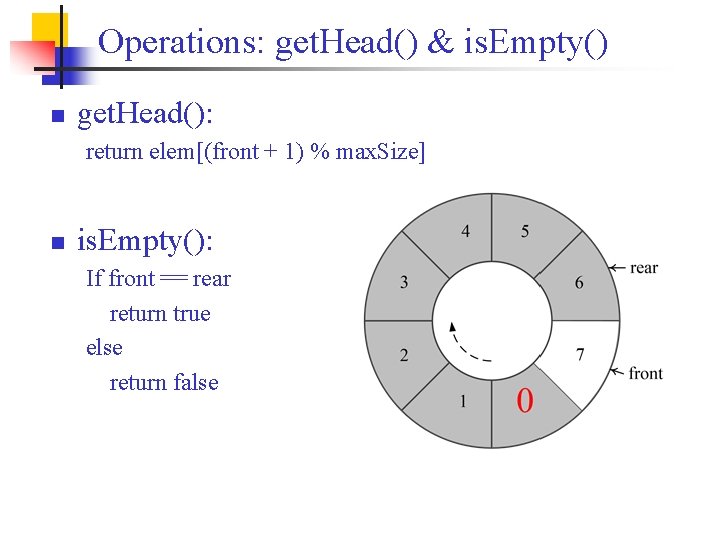
Operations: get. Head() & is. Empty() n get. Head(): return elem[(front + 1) % max. Size] n is. Empty(): If front == rear return true else return false

Outline n n Concept Implementation of Queue n n Implementation by sequence list Implementation by linked list Implementation of Queue Class Applications

Linked-List based Queue n Single linked list is good enough n n n front: points to the front node (for de. Queue) rear: points to the tail node (for en. Queue) head node: unnecessary

Features of Linked-List based Queue n n Linked list will never be full Linked list can be empty n n n front pointer = rear pointer = NULL No nodes in linked list de. Queue & en. Queue are simple: O(1)

Operation: create() n front = rear = NULL

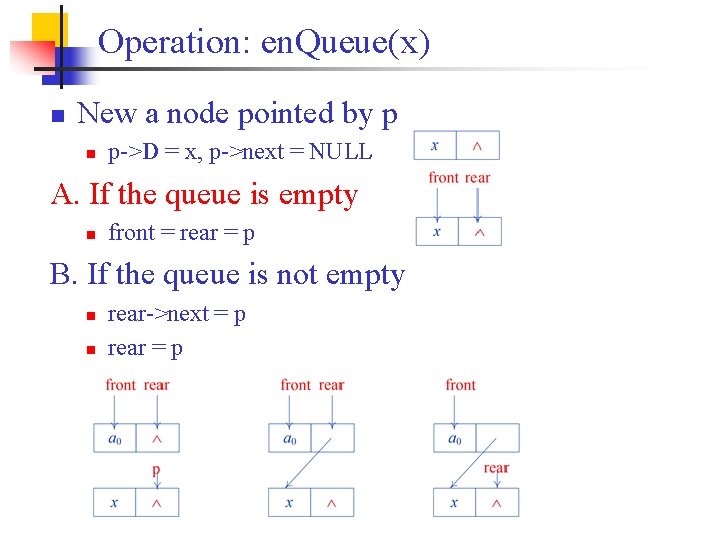
Operation: en. Queue(x) n New a node pointed by p n p->D = x, p->next = NULL A. If the queue is empty n front = rear = p B. If the queue is not empty n n rear->next = p rear = p

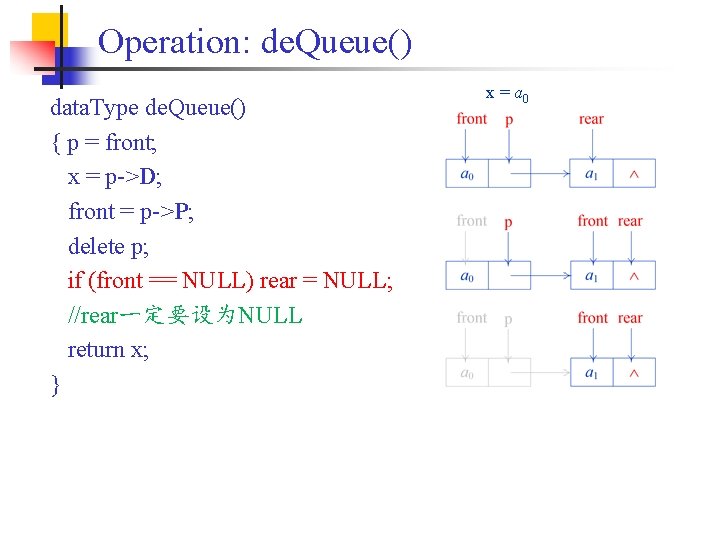
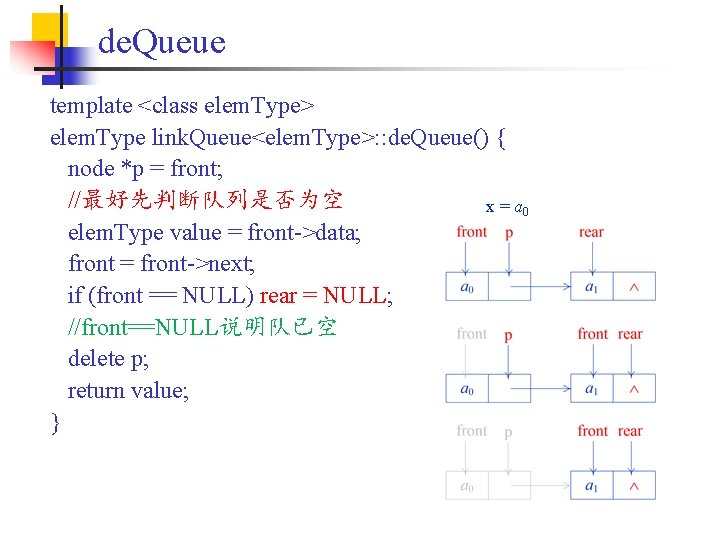
Operation: de. Queue() data. Type de. Queue() { p = front; x = p->D; front = p->P; delete p; if (front == NULL) rear = NULL; //rear一定要设为NULL return x; } x = a 0

Operations: get. Head() & is. Empty() n get. Head() n n return front->D is. Empty() if (front == NULL) return true else return false

Sequence List vs. Linked List n Time Complexity: n n However, operations of the sequence list look more complex than that of the linked list due to the circular structure Memory Complexity: n Memory is not fully utilized in the sequence list

Outline n n n Concept Implementation of Queue Class n n n Sequence list Linked list Applications

Abstract Class of Queue template <class elem. Type> class queue { public: virtual bool is. Empty() = 0; virtual void en. Queue(const elem. Type &x) = 0; virtual elem. Type de. Queue() = 0; virtual elem. Type get. Head() = 0; virtual ~queue() {} };

Circular Sequence Queue Class template <class elem. Type> class seq. Queue : public queue<elem. Type> { private: elem. Type *elem; int max. Size; //队列容量 int front, rear; //队头队尾地址标记 void double. Space(); //与第二章中的double. Space不同

Circular Sequence Queue Class public: seq. Queue(int size = 10) //构造函数初始化队列 { elem = new elem. Type[size]; max. Size = size; front = rear = 0; } //循环队列初始状态front=rear=0 ~seq. Queue() { delete elem; } bool is. Empty() { return front == rear; } void en. Queue(const elem. Type &x); elem. Type de. Queue(); elem. Type get. Head() { return elem[(front + 1) % max. Size]; } }; //front指向队头前一个单元

double. Space template <class elem. Type> void seq. Queue<elem. Type>: : double. Space() //要保持队列结构 { elem. Type *tmp =elem; elem = new elem. Type[2 * max. Size]; //申请新数组 for (int i = 1; i < max. Size; ++i) //i从1开始是因为新的front=0 elem[i] = tmp[(front + i) % max. Size]; //拷贝方式跟原来不同 //把原来的队头[(front + 1) % max. Size]放到elem[1] front = 0; rear = max. Size - 1; //重置队头队尾标志 max. Size *= 2; //max. Size跟着加倍，建立新的卷绕规则 delete tmp; }

en. Queue template <class elem. Type> void seq. Queue<elem. Type>: : en. Queue (const elem. Type &x) { if ((rear + 1) % max. Size == front) //循环数组已满 double. Space(); rear = (rear + 1) % max. Size; //此时max. Size已变成原来 2倍 //rear往后挪一位 elem[rear] = x; //并插入数据 }

de. Queue template <class elem. Type> elem. Type seq. Queue<elem. Type>: : de. Queue() { //此处或许该先判断一下队列是否已经为空 front = (front + 1) % max. Size; //front往后挪一个，即队头后移 return elem[front]; //返回原来队头的值 }

Outline n n n Concept Implementation of Queue Class n n n Sequence list Linked list Applications

Linked-List based Queue Class template <class elem. Type> class link. Queue: public queue<elem. Type> { private: struct node { elem. Type data; node *next; node(const elem. Type &x, node *N = NULL) { data = x; next = N; } node() : next(NULL) {} ~node() {} }; node *front, *rear;

Linked-List based Queue Class public: link. Queue() { front = rear = NULL; } ~link. Queue(); bool is. Empty() { return front == NULL; } //注意队空条件 void en. Queue(const elem. Type &x); elem. Type de. Queue(); elem. Type get. Head() { return front->data; } };

destructor template <class elem. Type> link. Queue<elem. Type>: : ~link. Queue() { node *tmp; while (front != NULL) { //从front开始顺序释放空间 tmp = front; front = front->next; delete tmp; } }

en. Queue template <class elem. Type> void link. Queue<elem. Type>: : en. Queue (const elem. Type &x) { //入队发生在链表尾部 if (rear == NULL) //如果队列为空 front = rear = new node(x); else { rear->next = new node(x); rear = rear->next; } }

de. Queue template <class elem. Type> elem. Type link. Queue<elem. Type>: : de. Queue() { node *p = front; //最好先判断队列是否为空 x = a 0 elem. Type value = front->data; front = front->next; if (front == NULL) rear = NULL; //front==NULL说明队已空 delete p; return value; }

Outline n n Concept Implementation of Queue Class Applications

Simulation of Queuing Systems n n It is a kind of cheap experiments, especially when the problem size is very large It is helpful to predict the system performance before implementation

Discrete Event System n Discrete events n n Arrival Departure custom n Observations n n Average waiting time Average queue length Server utilization ……

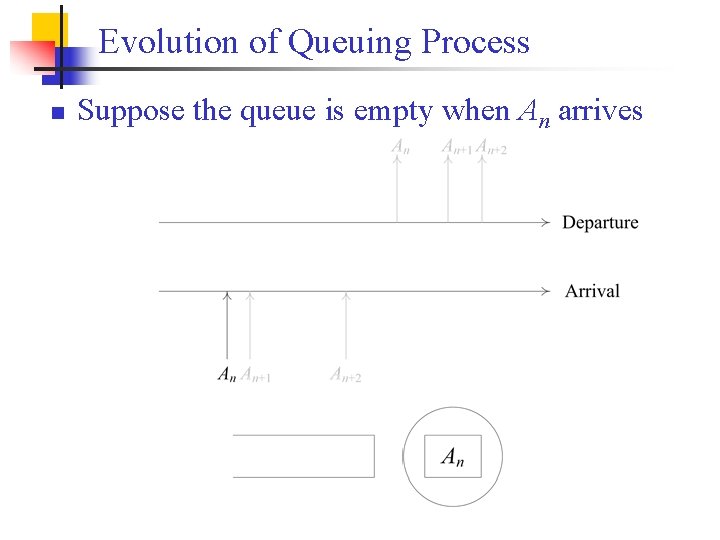
Evolution of Queuing Process n Suppose the queue is empty when An arrives

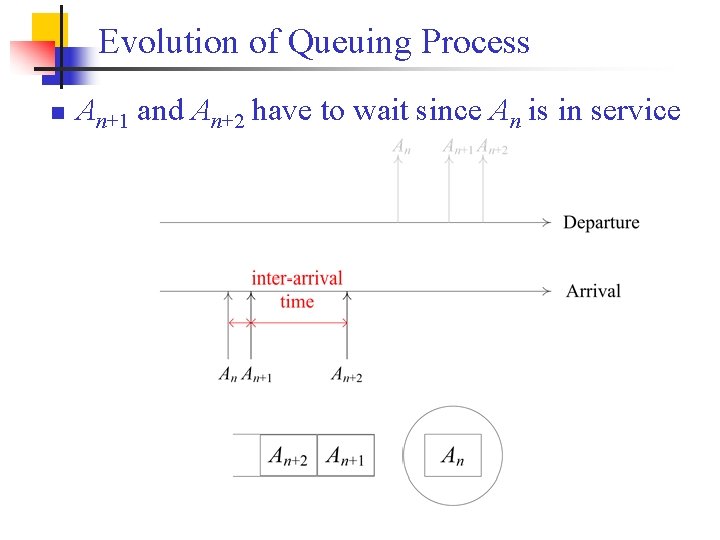
Evolution of Queuing Process n An+1 and An+2 have to wait since An is in service

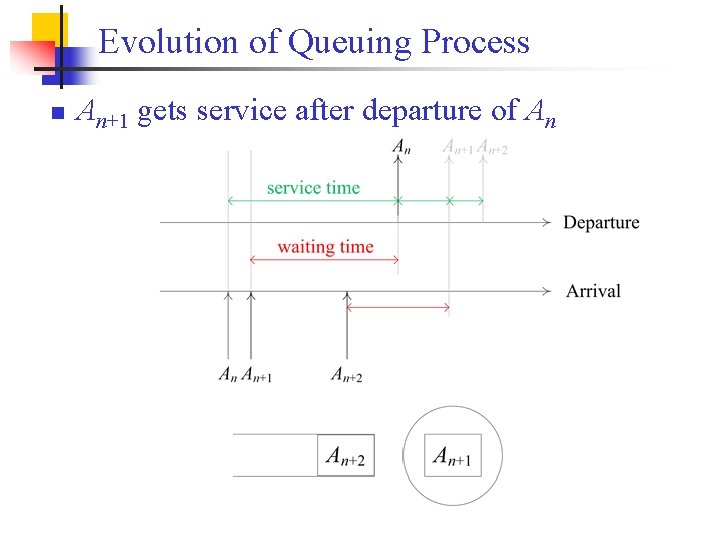
Evolution of Queuing Process n An+1 gets service after departure of An

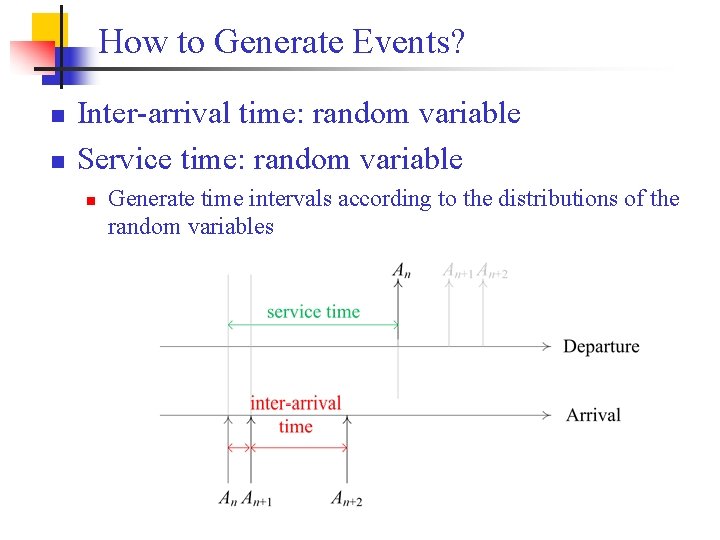
How to Generate Events? n n Inter-arrival time: random variable Service time: random variable n Generate time intervals according to the distributions of the random variables

Uniform Distributed Time Interval n

We Generate Arrival Events Now! n n n Generate first arrival time using random variable Generate second arrival time = first arrival time + inter-arrival time using random variable …

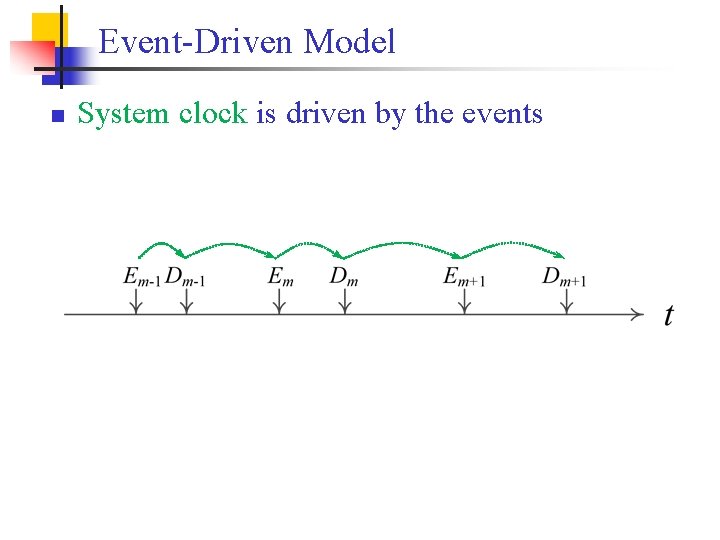
Event-Driven Model n System clock is driven by the events

Event-Driven Based Simulation n A queue is used to store the generated events n n Generate all arrival events and the time stamps en. Queue all arrival events according to the time stamps total. Wait. Time = 0 (waiting time of all customs) n while (queue is not empty), do n n the server serves the first arrival event in the queue once it becomes idle total. Wait. Time += waiting time of the first event Average waiting time = total. Wait. Time/N

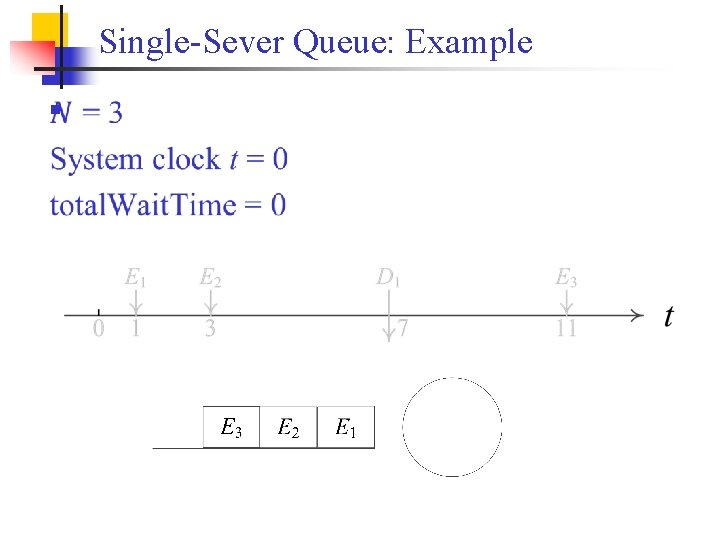
Single-Sever Queue: Example n

Single-Sever Queuing System: Example n

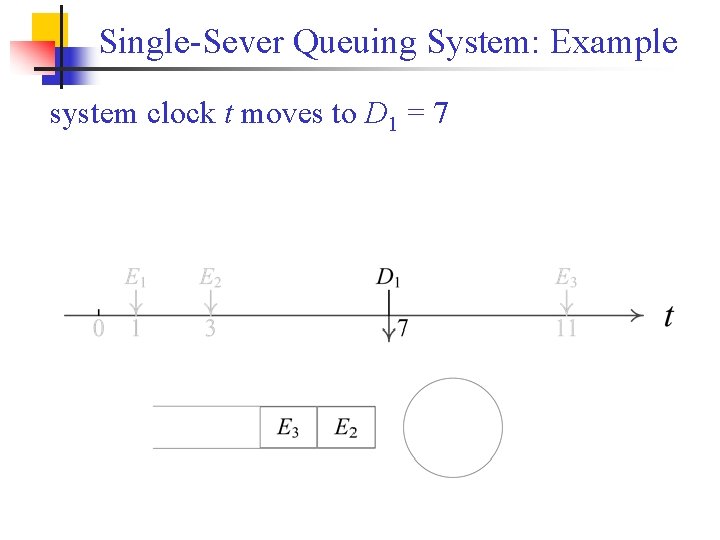
Single-Sever Queuing System: Example system clock t moves to D 1 = 7

Single-Sever Queuing System: Example E 2 is de. Queued and served by the server system clock t is still D 1 = 7 since D 1 > E 2 total. Wait. Time += D 1 - E 2 = 4 since D 1 > E 2 Generate the departure time D 2 for E 2

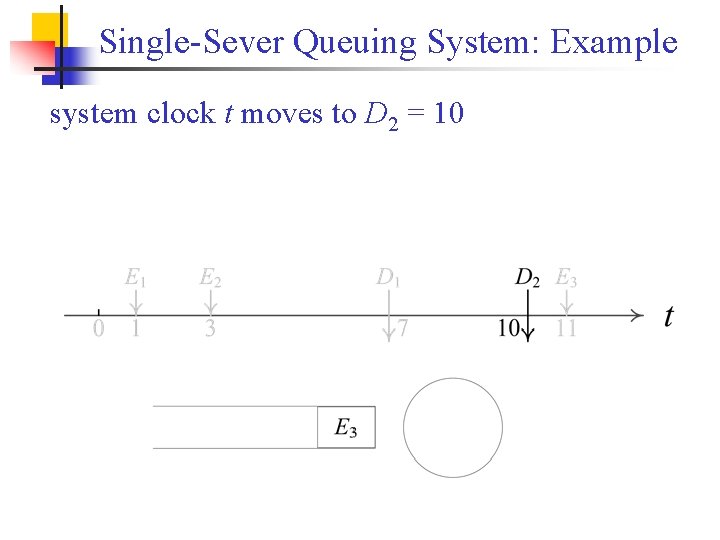
Single-Sever Queuing System: Example system clock t moves to D 2 = 10

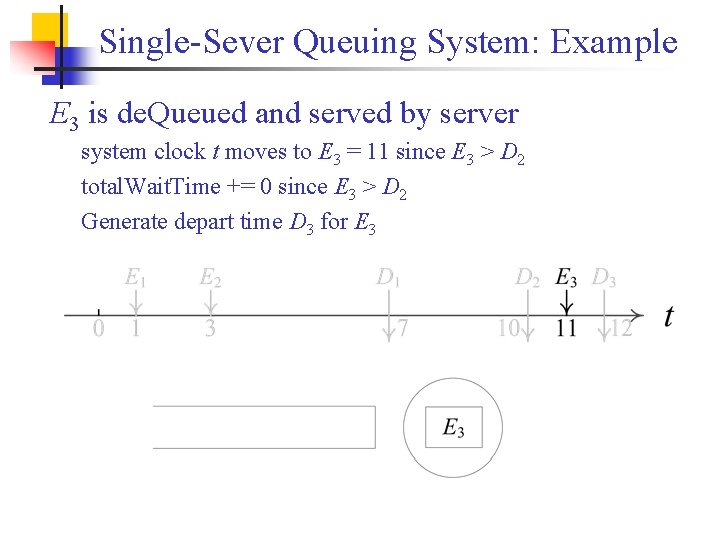
Single-Sever Queuing System: Example E 3 is de. Queued and served by server system clock t moves to E 3 = 11 since E 3 > D 2 total. Wait. Time += 0 since E 3 > D 2 Generate depart time D 3 for E 3

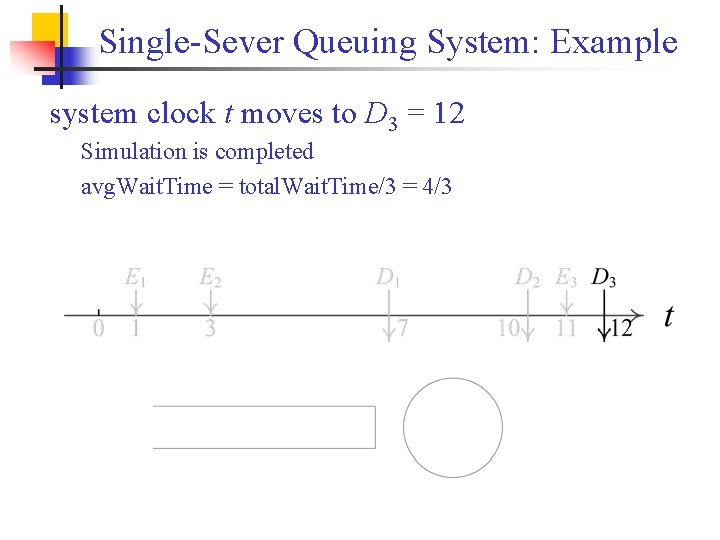
Single-Sever Queuing System: Example system clock t moves to D 3 = 12 Simulation is completed avg. Wait. Time = total. Wait. Time/3 = 4/3

Pseudo Code total. Wait. Time = 0; for (i=0; i<custom. Num; ++i) //产生所有顾客的到达时间 { generate an inter-arrival time; //产生到达时间间隔 arrival time of the next event += inter-arrival time; //产生下一顾客到达时间 en. Queue(next event); //下一顾客到达时间入队 } system time = 0; //时钟从0开始计时，仿真开始

Pseudo Code while (queue is not empty) //到达事件队列非空 { event = de. Queue; //时间最早的到达事件出队 if (arrival time > system time) system time = arrival time; //如果该到达事件的时间比系统时间大，说明没有等待 //系统时间推至该到达事件 else total. Wait. Time += (system time – arrival time); //有等待 generate departure time; //产生该到达事件的离去时间 system time = departure time; //系统时间拨到该离去事件时间 } return total. Wait. Time/number of events;

Simulation Class class simulator{ int arrival. Low; //到达时间间隔下限 int arrival. High; //到达时间间隔上限 //在[arrival. Low, arrival. High]产生随机整数 int service. Time. Low; //服务时间下限 int service. Time. High; //服务时间上限 //在[service. Time. Low, service. Time. High]产生随机整数 int custom. Num; //模拟顾客总数 public: simulator(); int avg. Wait. Time() const; };

Constructor simulator: : simulator() { cout << "请输入到达时间间隔的上下界："; cin >> arrival. Low >> arrival. High; cout << "请输入服务时间的上下界："; cin >> service. Time. Low >> service. Time. High; cout << "请输入模拟的顾客数："; cin >> custom. Num; srand(time(NULL)); //初始化随机数发生器 }

avg. Wait. Time() int simulator: : avg. Wait. Time() const //仿真实现主体 { int current. Time = 0; //当前时间(系统时钟) int total. Wait. Time = 0; //总的等待时间 int event. Time; //当前被执行的事件时间 link. Queue<int> customer. Queue; //基于链表的队列(节省空间) //链表有利于边执行边释放，以节省系统内存 int i; for (i=0; i<custom. Num; ++i) { current. Time += arrival. Low + (arrival. High - arrival. Low +1) * rand() / (RAND_MAX + 1); //产生每个顾客的到达时间 customer. Queue. en. Queue(current. Time); //到达事件入队 }

avg. Wait. Time() current. Time = 0; //系统时间从0开始计时 while (!customer. Queue. is. Empty()) //如果到达事件队列不为空 { event. Time = customer. Queue. de. Queue(); //出队队首到达事件 if (event. Time < current. Time) //队首到达事件时间<当前时间 total. Wait. Time += current. Time - event. Time; //说明队首事件 //有等待 else current. Time = event. Time; //否则系统时间更新为队首事 //件时间(队首事件无等待) current. Time += service. Time. Low + (service. Time. High -service. Time. Low +1) * rand() / (RAND_MAX + 1); //将系统时间调到队首到达事 //件的离去时间 } return total. Wait. Time / custom. Num; }

Further Reading n portal. sjtu. edu. cn/离散事件仿真. pdf n 第五、六章

Homework n 1

Appendix

Problem n

Our Approach: before Simulation n Generate the first arrival event n n n en. Queue this event sys. Clock = time of this event next. Arrival = sys. Clock + inter-arrival time //后续流程没有考虑各种指标的累加，只是一 个演进的框架。有兴趣的同学可以在这个基 础上继续修改。 //此处感谢杜辰和张智锋的协助！

Our Approach: during Simulation n

Our Approach: during Simulation n

Our Approach: Advantage Memory requirement is low n The simulation runs out of memory only if the queueing system is unstable (input rate > service rate) n