Chapter 4 Quadratic Equations 4 1 Graphical Solutions

Chapter 4 Quadratic Equations

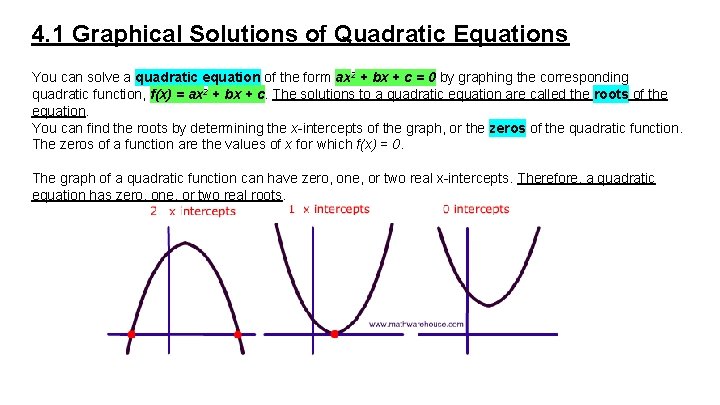
4. 1 Graphical Solutions of Quadratic Equations You can solve a quadratic equation of the form ax 2 + bx + c = 0 by graphing the corresponding quadratic function, f(x) = ax 2 + bx + c. The solutions to a quadratic equation are called the roots of the equation. You can find the roots by determining the x-intercepts of the graph, or the zeros of the quadratic function. The zeros of a function are the values of x for which f(x) = 0. The graph of a quadratic function can have zero, one, or two real x-intercepts. Therefore, a quadratic equation has zero, one, or two real roots.

4. 2 Factoring Quadratic Equations Another way of solving a quadratic equation is by factoring. To solve the equation: - first write the equation in the form of ax 2 + bx + c = 0 - then factor the left side - Next, set each factor to zero and solve for the unknown Ex. x 2 + 8 x = -12 x 2 + 8 x + 12 = 0 (x + 6)(x + 2) = 0 x+2=0 x=-2 or or x+6=0 x=-6 Check both answers by substituting the x value: (-2)2 + 8(-2) = - 12 4 - 16 = - 12 -12 = - 12 ✓ (-6)2 + 8(-6) = -12 36 - 48 = -12 ✓

4. 3 Solving the Quadratic Equation by Completing the Square As recalled, completing the square is the process of rewriting a quadratic polynomial from the standard form ax 2 + bx + c, to the vertex form, a(x - p)2 + q. You can use this method to determine the roots of a quadratic equation. Ex. (x - 1)2 2 x 2 - 4 x - 2 = 0 x 2 - 2 x - 1 = 0 x 2 - 2 x = 1 x 2 - 2 x + 1 = 1 + 1 = 2 √(x - 1)2 = √ 2 x - 1 = ±√ 2 x = ±√ 2 + 1 +√ 2 + 1 ≈ 2. 41 x ≈ 2. 41 Divide both sides by a common factor of 2 Isolate the variable terms on the left side Complete the square on both sides Take the square root of both sides -√ 2 + 1 ≈ -0. 41 x ≈ -0. 41

4. 4 The Quadratic Formula An alternate method to solve a quadratic equation is using the quadratic formula in the form of ax 2 + bx + c = 0. The formula is: x = -b 2 ± √ b 2 - 4 ac 2 a There is also the discriminant which is the expression b 2 - 4 ac located under the radical sign in the formula. You can use the discriminant to determine the nature of the roots for a quadratic equation. - when the value of the discriminant is positive, b 2 - 4 ac > 0, there are two distinct roots when the value of the discriminant is zero, b 2 - 4 ac = 0, there is one distinct root when the value of the discriminant is negative, b 2 - 4 ac < 0, there are no real roots

Example: Use the quadratic formula to solve 6 x 2 - 14 x + 8 = 0 x = -b 2 ± √ b 2 - 4 ac 2 a x = -(-14) ± √ (-14)2 - 4(6)(8) 2(8) x = 14 ± √ 4 16 x = 14 ± 2 16 x = 14 + 2 16 x = 16 16 x=1 or x = 14 - 2 16 x = 12 16 x=3 4