Chapter 4 Probability Statistics Section 4 2 Simple

Chapter 4: Probability & Statistics Section 4. 2: Simple Probability & Odds APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

Terminology Outcome: The result of an experiment. Event: A single or a collection of outcomes. Sample Space: The list of all possible outcomes of an experiment. Theoretical Probability: The predicted likelihood of obtaining a specific event. What should happen, based on the math. Relative Frequency: Computing the likelihood of an event based on the results of an experiment. What has already happened. IMPORTANT Use the term “probability” for a predicted theoretical probability, and “frequency” for relative frequency. APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

Probability The probability of an event is the ratio of the successful outcomes to all the possible outcomes. If something cannot happen, there are no successes. Thus, the probability of an event that cannot happen is 0. If something happens 100% of the time, every outcome is a success. Thus, the probability of an event that must happen is 1. All probabilities must be between 0 and 1, inclusive, and we will write them as fractions. Example: A jar contains 11 red marbles and 30 green marbles. If you randomly pick one marble from the jar, what is the probability of picking a red marble? P(red) = 11/41 APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

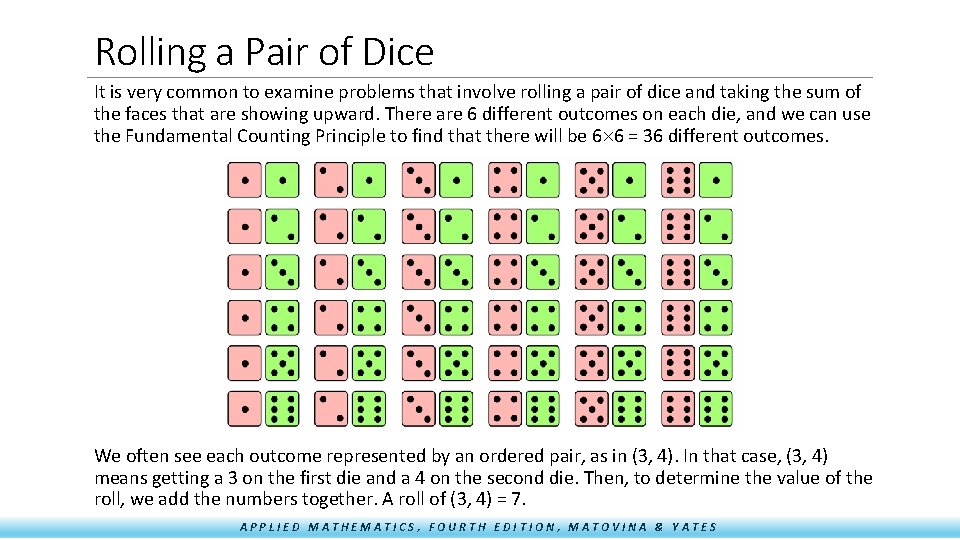
Rolling a Pair of Dice It is very common to examine problems that involve rolling a pair of dice and taking the sum of the faces that are showing upward. There are 6 different outcomes on each die, and we can use the Fundamental Counting Principle to find that there will be 6 6 = 36 different outcomes. We often see each outcome represented by an ordered pair, as in (3, 4). In that case, (3, 4) means getting a 3 on the first die and a 4 on the second die. Then, to determine the value of the roll, we add the numbers together. A roll of (3, 4) = 7. APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

Rolling a Pair of Dice - Examples Example: Two dice are rolled, and the sum of the faces is obtained. Find the probability that the sum is 9. There are four ways to get a 9 - (3, 6), (4, 5), (5, 4), and (6, 3) – and 36 possible outcomes. P(9) = 4/36 Example: Two dice are rolled, and the sum of the faces is obtained. Find the probability that the sum is 15. This cannot happen. P(15) = 0 Example: Two dice are rolled, and the sum of the faces is obtained. Find the probability that the sum is greater than 9. The sum has to be 10, 11, or 12. There are three ways to get a 10, two ways to get 11, and one way to get a 12. P(> 9) = 6/36 APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

Drawing a Card There are 52 cards in a standard deck, and they are divided into four suits, as follows: v v Spades: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King Clubs: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King Hearts: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King Diamonds: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King Since the Jack, Queen, and King of each suit have pictures of people on them, they are often referred to as "face cards. ” Be careful. For an OR event, at least one of the outcomes must be a success, but having more than one is also a success. For an AND event, all of the listed outcomes must be successes. Example: Answer “Yes” or “No. ” Is this text black OR white? The answer is “Yes. ” For the OR statement, only one of the conditions needs to be true for a “Yes” answer. APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

Drawing a Card - Examples: If you draw a single card from a standard deck of cards, find: a. P(Spade) There are 13 Spades. P(Spade) = 13/52 b. P(4 OR a Club) 13 Clubs and 3 more 4 s (don’t count the 4 of Clubs twice). P(4 OR Club) = 16/52 c. P(Face Card AND a Heart) There are 3 Face Cards that are also are Hearts. P(Face Card AND Heart) = 3/52 APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES

Odds The odds against an event are computed as the ratio of failures to successes and are written as a ratio (two numbers separated by a colon or the word “to”). If we know the odds against an event are 10 to 1, in 11 identical attempts, we should expect 10 failures and 1 success of the event in question. Do not include the total number of outcomes in odds statements. The numbers in the odds statement indicate the fails and successes. Examples: A gumball machine has 14 red gumballs, 12 white gumballs and 4 yellow gumballs in it. If you purchase one gumball at random: a. What is the probability that the purchased gumball will be red? P(red) = 14/30 b. What are the odds against getting a yellow gumball? # of Fails to # of Success = 26 to 4 APPLIED MATHEMATICS, FOURTH EDITION, MATOVINA & YATES