Chapter 4 Prediction Predictor and Criterion Variables Predictor

Chapter 4 Prediction

Predictor and Criterion Variables § Predictor variable (X) § Criterion variable (Y)

Prediction Using Z Scores § Prediction model – Predicted Z score (on criterion variable) = standardized regression coefficient multiplied by Z score on predictor variable – Formula

Prediction Using Z Scores § The standardized regression coefficient (β) – In bivariate prediction, β = r

Raw-Score Prediction Using the Z-Score Prediction Model 1. Change raw score on predictor to a Z score 2. Multiply β by the predictor variable Z score

Raw-Score Prediction Using the Z-Score Prediction Model 3. Change the predicted Z score on the criterion variable to a raw score

Raw Score Prediction Using the Direct Raw-Score Prediction Model § Direct raw-score prediction model – Predicted raw score (on criterion variable) = regression constant plus the result of multiplying a raw-score regression coefficient by the raw score on the predictor variable – Formula

Raw Score Prediction Using the Direct Raw-Score Prediction Model § The regression constant (a) – Predicted raw score on criterion variable when raw score on predictor variable is 0 § Raw-score regression coefficient (b) – How much the predicted criterion variable increases for every increase of 1 on the predictor variable

Raw Score Prediction Using the Direct Raw-Score Prediction Model 1. Figure the regression constant (a) 2. Figure the raw-score regression coefficient (b) 3. Find predicted raw score on the criterion variable

The Regression Line § Relation between predictor variable and predicted values of the criterion variable § Slope of regression line – Equals b, the raw-score regression coefficient § Intercept of the regression line – Equals a, the regression constant

Drawing the Regression Line 1. Draw and label the axes for a scatter diagram 2. Figure predicted value on criterion variable for a low value on predictor variable – mark point on graph 3. Repeat step 2. with a high value on predictor variable 4. Draw a line passing through the two marks

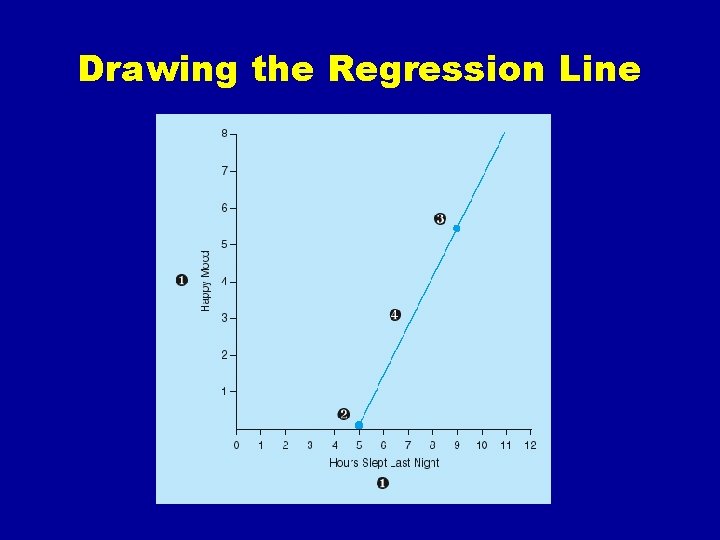
Drawing the Regression Line

Error and Proportionate Reduction in Error § Error – Actual score minus the predicted score § Proportionate reduction in error – Squared error using prediction model = SSError – Total squared error when predicting from the mean = SSTotal

Error and Proportionate Reduction in Error § Formula for proportionate reduction in error: § Proportionate reduction in error = r 2 § Proportion of variance accounted for

Multiple Regression § Bivariate prediction § Multiple correlation § Multiple regression

Multiple Regression § Multiple regression prediction models – Each predictor variable has its own regression coefficient – e. g. , Z-score multiple regression formula with three predictor variables:

Limitations of Regression § Regression inaccurate if – Correlation is curvilinear – Restriction in range – Unreliable measures

Controversies and Limitations § Controversy about how to judge the relative importance of each predictor variable in predicting the dependent variable § Consider both the rs and the βs

Prediction in Research Articles § Bivariate prediction models rarely reported § Multiple regression results commonly reported