Chapter 4 Part a The Expectation and Variance

Chapter 4: Part a – The Expectation and Variance of Distributions We will be discussing q The Algebra of Expectation q The Algebra of Variance q The Normal Distribution (These topics are needed for Chapter 5) Mathematical Marketing 1

The Expectation of a Discrete Random Variable Assume we have a random variable, ai. If ai can take on only certain values: 1, 2, ···, J, then we have as the definition of Expectation of ai, or E(ai) Mathematical Marketing 2

The Expectation of a Continuous Variable Imagine we have a scalar, ai, that can take on any possible values with probability f(ai), i. e. f(ai) ai By definition, the expectation of that scalar is Mathematical Marketing 3

Three Rules for E(·) The Expectation of a Constant is That Constant E(c) = c The Expectation of a Sum is the Sum of the Expectations E(a + b) = E(a) + E(b) In the Expectation of a Linear Combination, a Constant Matrix Can Pass Through E(·) E(Da) = DE(a) E(a′F) = E(a′)F Mathematical Marketing 4

The Variance of a Random Variable The Variance of the Random Vector a is Given by Mathematical Marketing 5

The Variance of a Mean Centered Vector If E(a) = 0, i. e. a is mean centered, we have just V(a) = E(aa′) NB – just because E(a) = 0 doesn’t mean that E(aa′) = 0! Mathematical Marketing 6

The Variance Matrix For mean centered a, we have V(a) = E(aa′) Mathematical Marketing 7

Two Rules for V(·) Adding a Constant Vector Does Not Change the Variance V(a + c) = V(a) The Variance of a Linear Combination is a Quadratic Form V(Da) = DV(a)D′ Hint: The Above Theorem Will Figure Many Times in What Is to Come! Mathematical Marketing 8

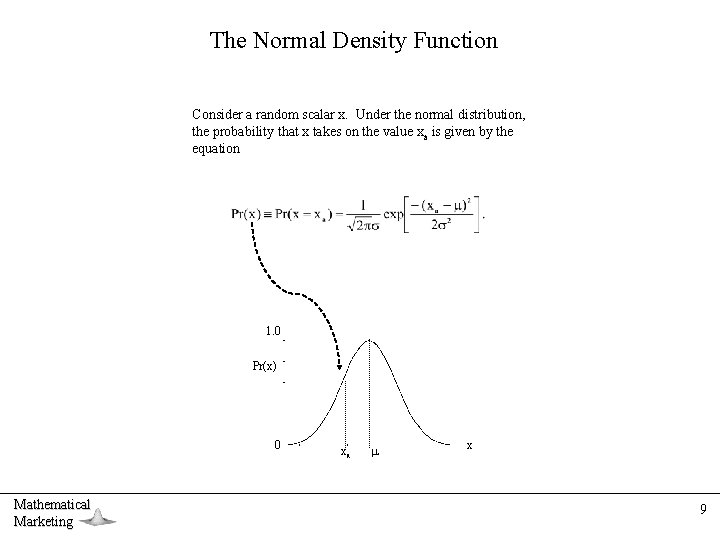
The Normal Density Function Consider a random scalar x. Under the normal distribution, the probability that x takes on the value xa is given by the equation 1. 0 Pr(x) 0 Mathematical Marketing xa x 9

The Standard Normal Density If = 0 and 2 = 1, so that z = (x - ) / the expression simplifies to Note very common notation Mathematical Marketing 10

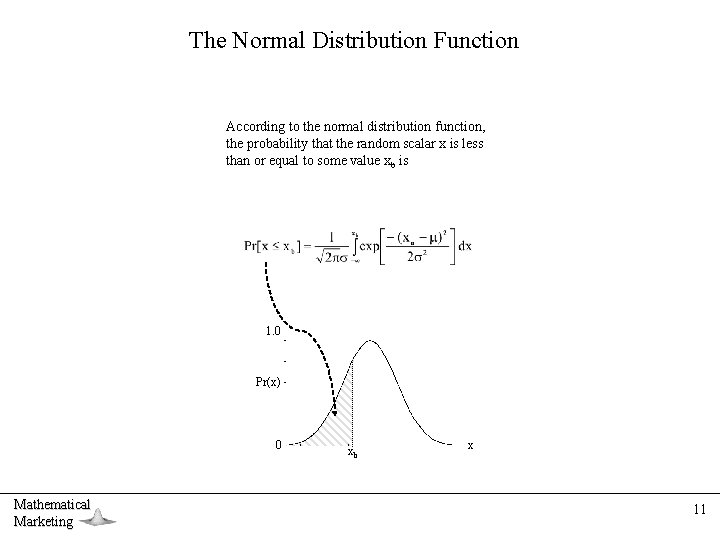
The Normal Distribution Function According to the normal distribution function, the probability that the random scalar x is less than or equal to some value xb is 1. 0 Pr(x) 0 Mathematical Marketing xb x 11

Other Notational Conventions For our scalar x that is distributed according to the normal distribution function, we say x ~ N( , 2). Mathematical Marketing 12

The Standardized Normal Distribution If we set z = (x - ) / then Again, note the notational convention and that Mathematical Marketing 13

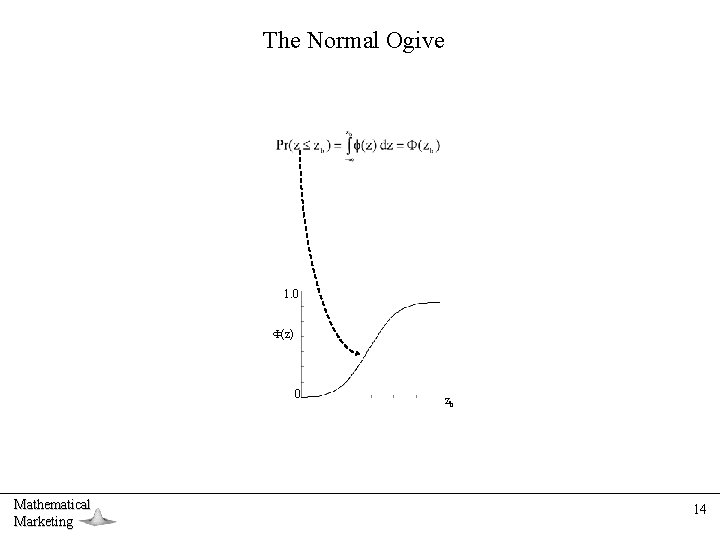
The Normal Ogive 1. 0 (z) 0 Mathematical Marketing zb 14