Chapter 4 Molecular Symmetry Dr S M Condren

Symmetry Elements and Symmetry Operations • • • Identity Proper axis of rotation Mirror

Symmetry Elements and Symmetry Operations • Identity => E Dr. S. M. Condren

Symmetry Elements and Symmetry Operations • Proper axis of rotation => Cn – where

2 -Fold Axis of Rotation Dr. S. M. Condren

3 -Fold Axis of Rotation Dr. S. M. Condren

Rotations for a Trigonal Planar Molecule Dr. S. M. Condren

Symmetry Elements and Symmetry Operations Mirror planes => sh => mirror plane perpendicular to

Mirrors sv sv Cl Cl sh I sd Cl Dr. S. M. Condren

Rotations and Mirrors in a Bent Molecule Dr. S. M. Condren

Symmetry Elements and Symmetry Operations • Center of symmetry => i Dr. S. M.

Symmetry Elements and Symmetry Operations • Improper axis of rotation => Sn – rotation

Improper Rotation in a Tetrahedral Molecule Dr. S. M. Condren

S 1 and S 2 Improper Rotations Dr. S. M. Condren

Successive C 3 Rotations on Trigonal Pyramidal Molecule Dr. S. M. Condren

Selection of Point Group from Shape • first determine shape using Lewis Structure and

Selection of Point Group from Shape 1. determine the highest axis of rotation 2.

Orbital Symmetry, pz z E + C 2 v X(E) = +1 - +

Orbital Symmetry, py - z E X(E) = +1 + - + C 2(z)

Orbital Symmetry, px z - E y + + X(E) = +1 C 2(z)

Water, C 2 v Point Group Translational motion in y z y x o

Water, C 2 v Point Group Translational motion in y z o H H

Water, C 2 v Point Group Translational motion in y z y C 2(z)

Water, C 2 v Point Group Translational motion in y Representation: E C 2(z)

Water, C 2 v Point Group Rotation about z axis z O r. H

Water, C 2 v Point Group Rotation about z axis Representation E C 2(z)

Water, C 2 v Point Group Representations: Rotation E C 2(z) G 4 +1

Water, C 2 v Point Group Representation: Translation E C 2(z) G 1 +1

Water, C 2 v Point Group Representation: Rotation E C 2(z) G 4 +1

Water, C 2 v Point Group Character Table E C 2(z) A 1 +1

Vibrational Modes in CO 2 For linear molecules: 3 N - 5 IR fundamentals

Vibrational Modes in SO 2 For non-linear molecules: 3 N - 6 IR fundamentals

Vibration Modes for SO 3 For non-linear molecules: 3 N - 6 IR fundamentals

Vibrational Modes for CH 4 For non-linear molecules: 3 N - 6 IR fundamentals

Vibrational Modes for [Pt. Cl 4]-2 For non-linear molecules: 3 N - 6 IR

Slides: 54

Download presentation

Chapter 4 Molecular Symmetry Dr. S. M. Condren

Dr. S. M. Condren

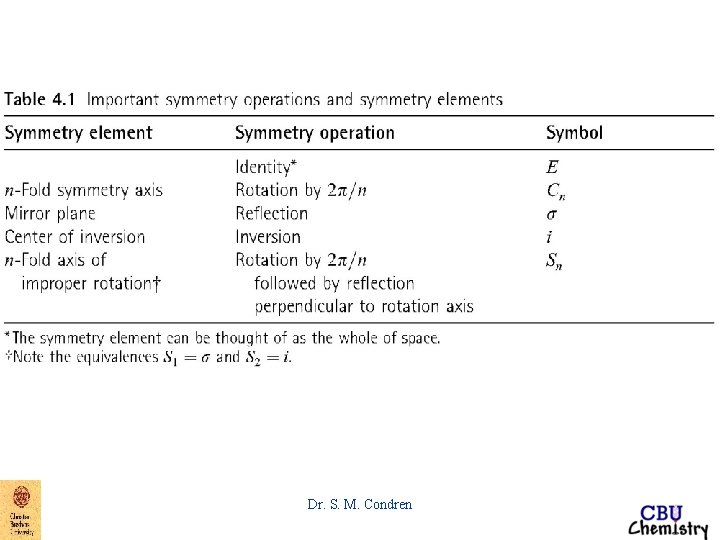
Symmetry Elements and Symmetry Operations • • • Identity Proper axis of rotation Mirror planes Center of symmetry Improper axis of rotation Dr. S. M. Condren

Symmetry Elements and Symmetry Operations • Identity => E Dr. S. M. Condren

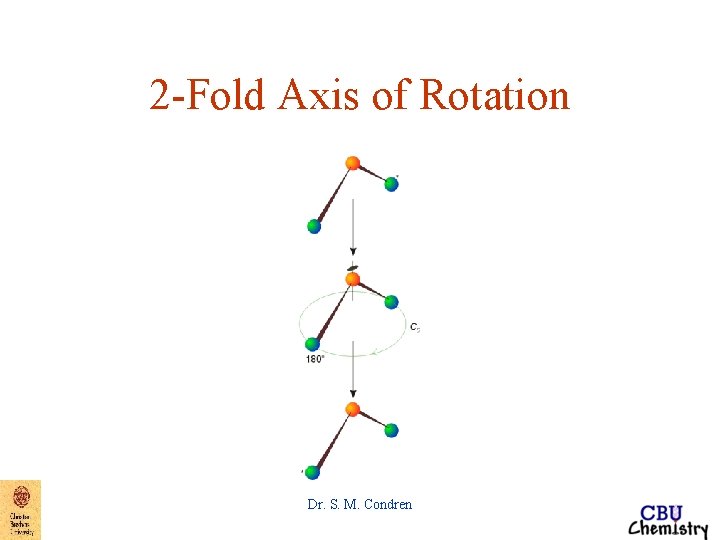
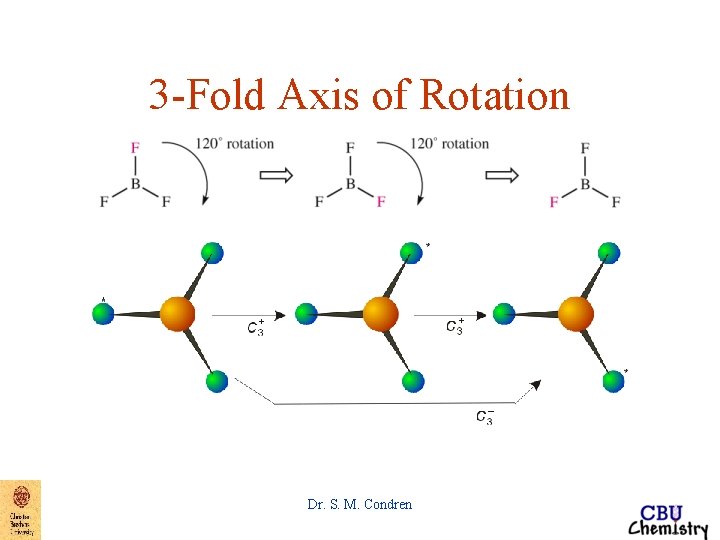
Symmetry Elements and Symmetry Operations • Proper axis of rotation => Cn – where – – n = 2, 180 o rotation n = 3, 120 o rotation n = 4, 90 o rotation n = 6, 60 o rotation n = , (1/ )o rotation • principal axis of rotation, Cn Dr. S. M. Condren

2 -Fold Axis of Rotation Dr. S. M. Condren

3 -Fold Axis of Rotation Dr. S. M. Condren

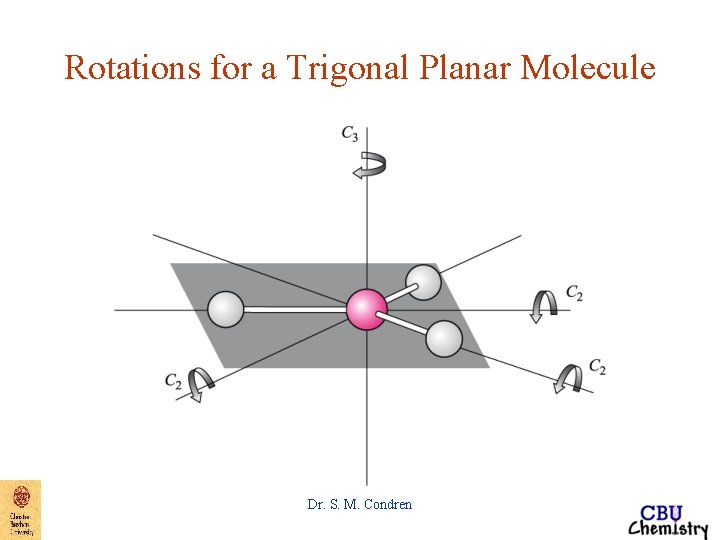
Rotations for a Trigonal Planar Molecule Dr. S. M. Condren

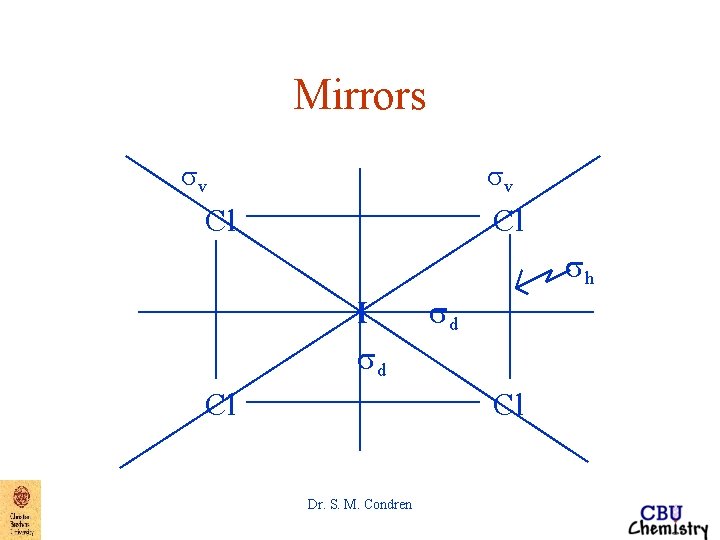
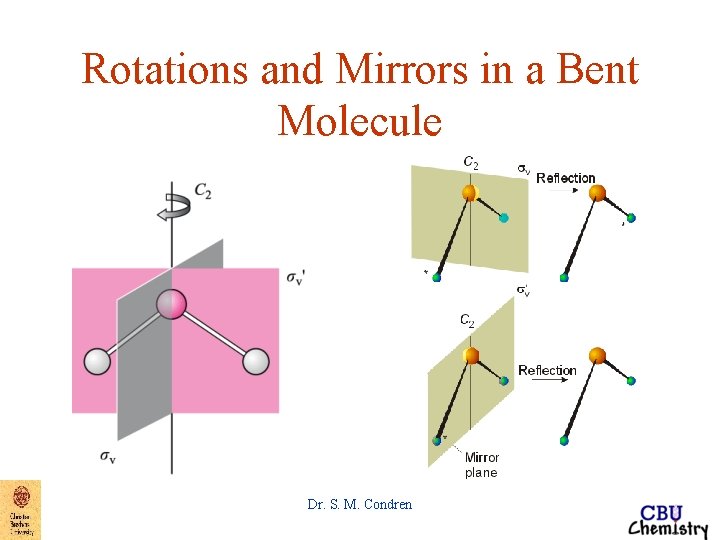
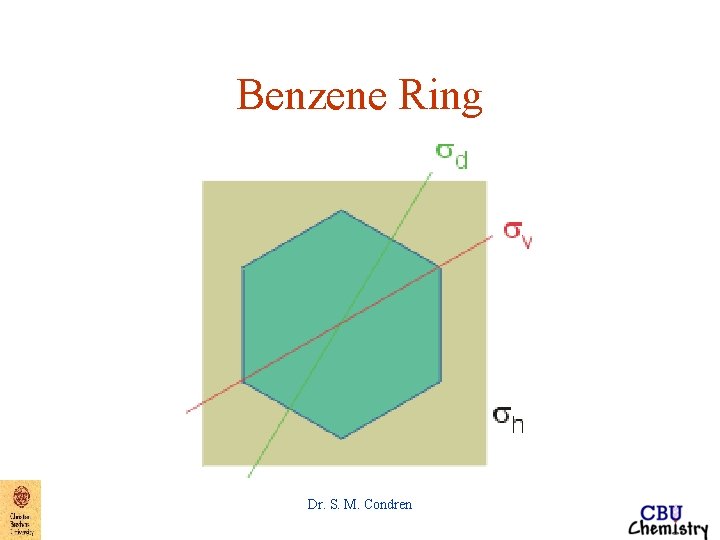
Symmetry Elements and Symmetry Operations Mirror planes => sh => mirror plane perpendicular to a principal axis of rotation sv => mirror plane containing principal axis of rotation sd => mirror plane bisects dihedral angle made by the principal axis of rotation and two adjacent C 2 axes perpendicular to principal rotation axis Dr. S. M. Condren

Mirrors sv sv Cl Cl sh I sd Cl Dr. S. M. Condren

Rotations and Mirrors in a Bent Molecule Dr. S. M. Condren

Benzene Ring Dr. S. M. Condren

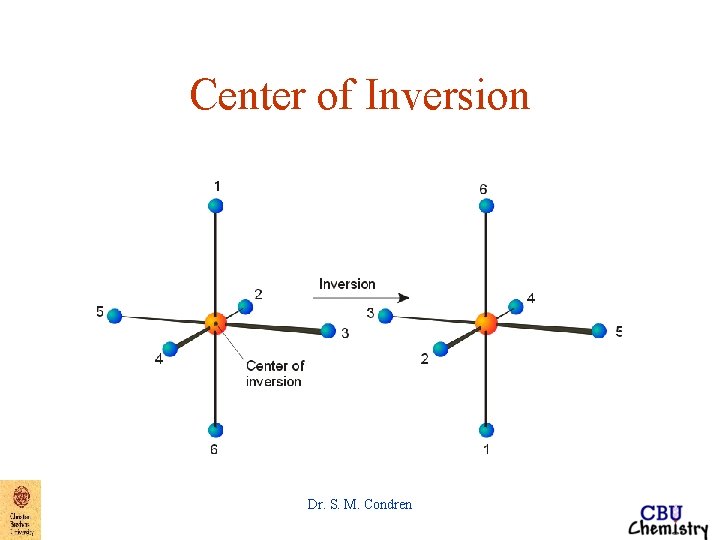
Symmetry Elements and Symmetry Operations • Center of symmetry => i Dr. S. M. Condren

Center of Inversion Dr. S. M. Condren

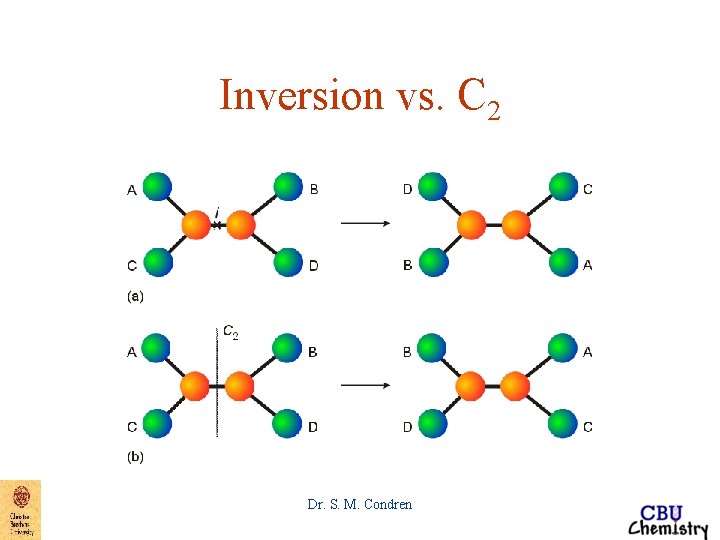
Inversion vs. C 2 Dr. S. M. Condren

Symmetry Elements and Symmetry Operations • Improper axis of rotation => Sn – rotation about n axis followed by inversion through center of symmetry Dr. S. M. Condren

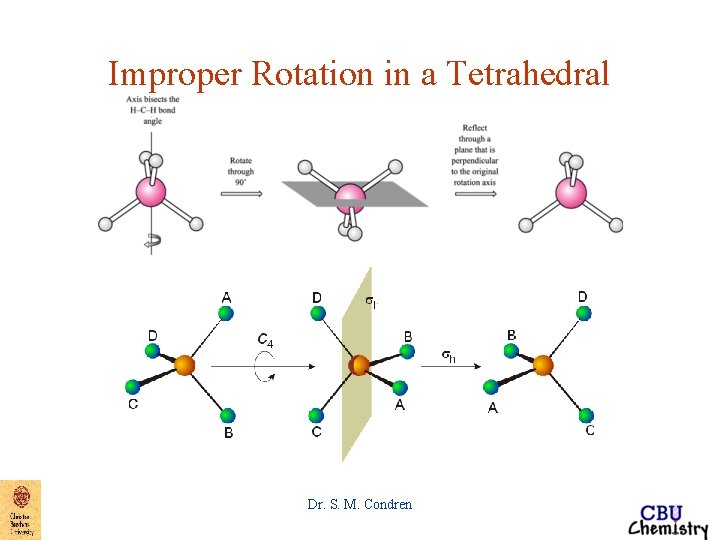
Improper Rotation in a Tetrahedral Molecule Dr. S. M. Condren

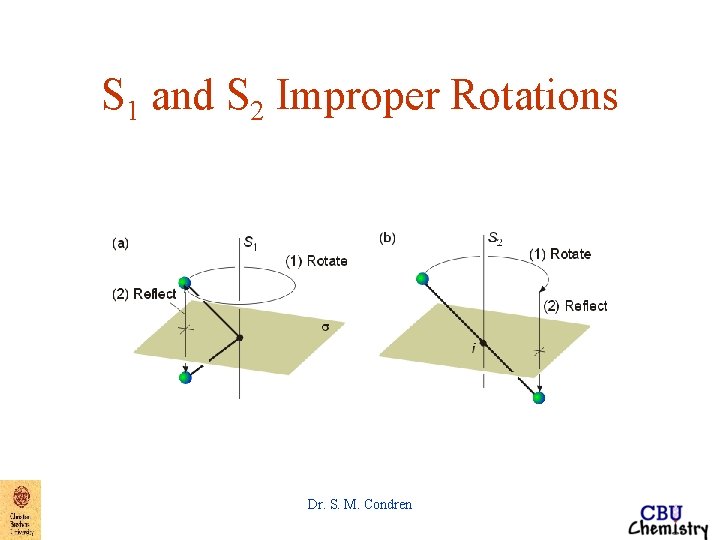
S 1 and S 2 Improper Rotations Dr. S. M. Condren

Successive C 3 Rotations on Trigonal Pyramidal Molecule Dr. S. M. Condren

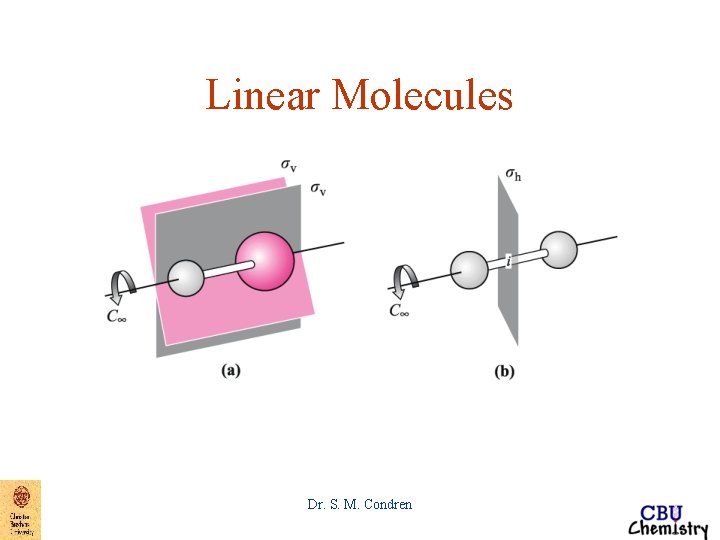
Linear Molecules Dr. S. M. Condren

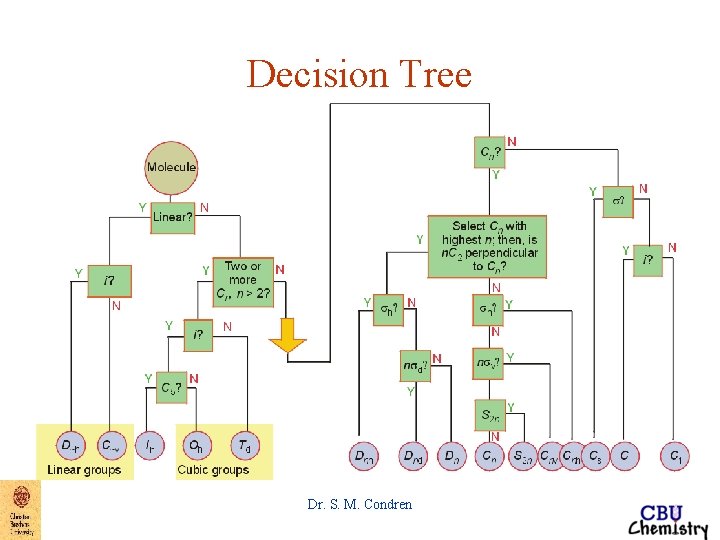
Selection of Point Group from Shape • first determine shape using Lewis Structure and VSEPR Theory • next use models to determine which symmetry operations are present • then use the flow chart Figure 3. 9, Pg. 81 text to determine the point group Dr. S. M. Condren

Dr. S. M. Condren

Decision Tree Dr. S. M. Condren

Selection of Point Group from Shape 1. determine the highest axis of rotation 2. check for other non-coincident axis of rotation 3. check for mirror planes Dr. S. M. Condren

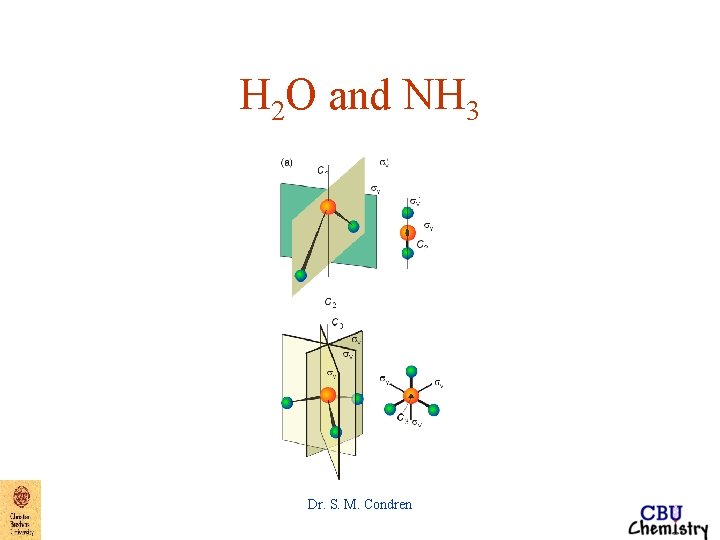
H 2 O and NH 3 Dr. S. M. Condren

Dr. S. M. Condren

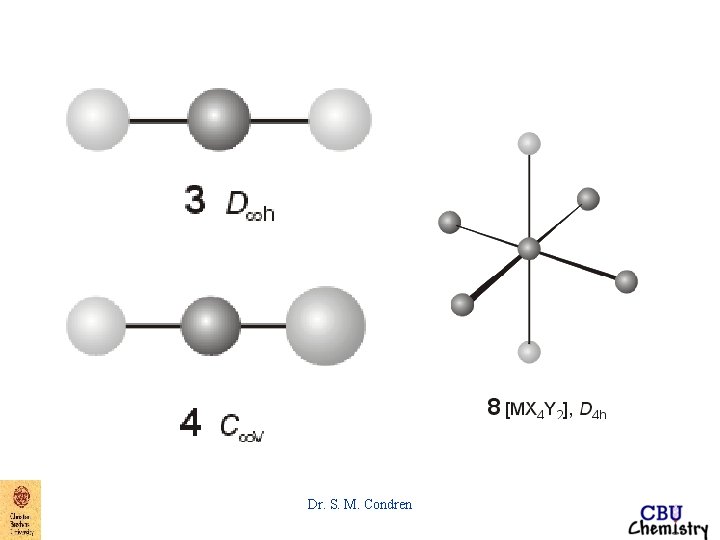
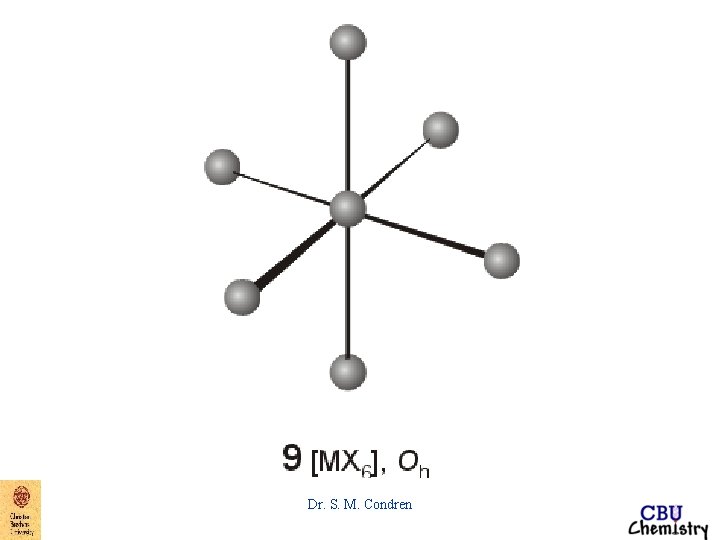
Geometric Shapes Dr. S. M. Condren

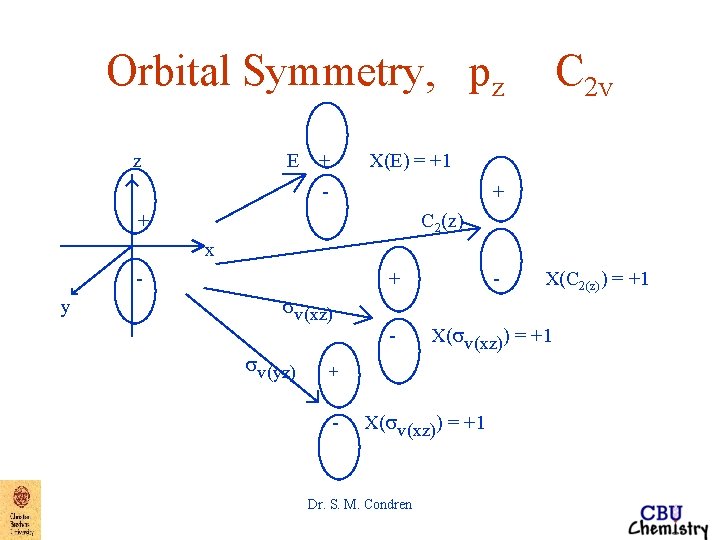
Orbital Symmetry, pz z E + C 2 v X(E) = +1 - + + C 2(z) x y sv(xz) sv(yz) + - - X(sv(xz)) = +1 + - X(sv(xz)) = +1 Dr. S. M. Condren X(C 2(z)) = +1

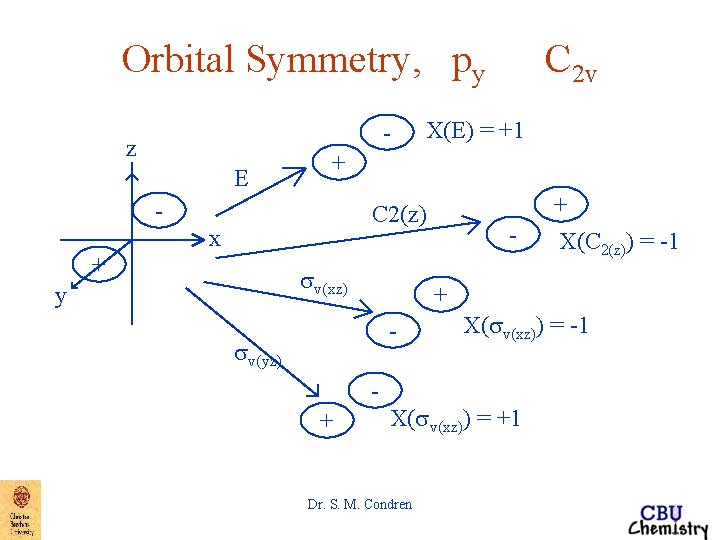
Orbital Symmetry, py - z E X(E) = +1 + - + C 2(z) x + sv(xz) y C 2 v + - sv(yz) X(sv(xz)) = -1 + X(C 2(z)) = -1 X(sv(xz)) = +1 Dr. S. M. Condren

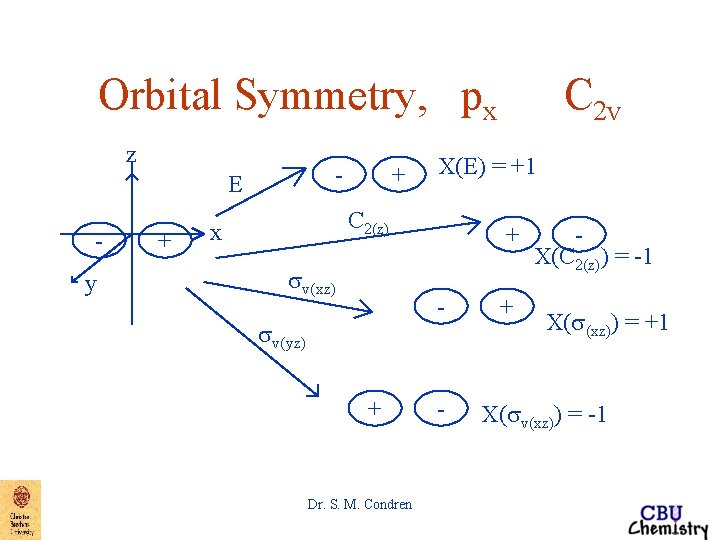
Orbital Symmetry, px z - E y + + X(E) = +1 C 2(z) x sv(xz) + - sv(yz) + Dr. S. M. Condren C 2 v - + X(C 2(z)) = -1 X(s(xz)) = +1 X(sv(xz)) = -1

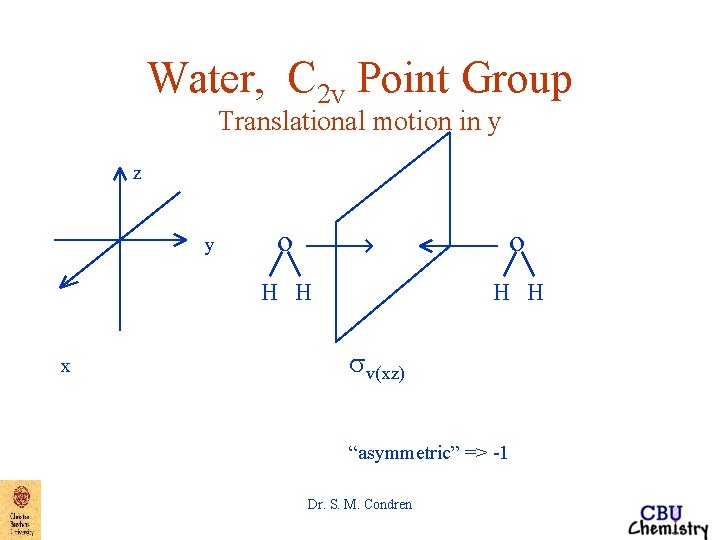
Water, C 2 v Point Group Translational motion in y z y x o o H H sv(xz) “asymmetric” => -1 Dr. S. M. Condren

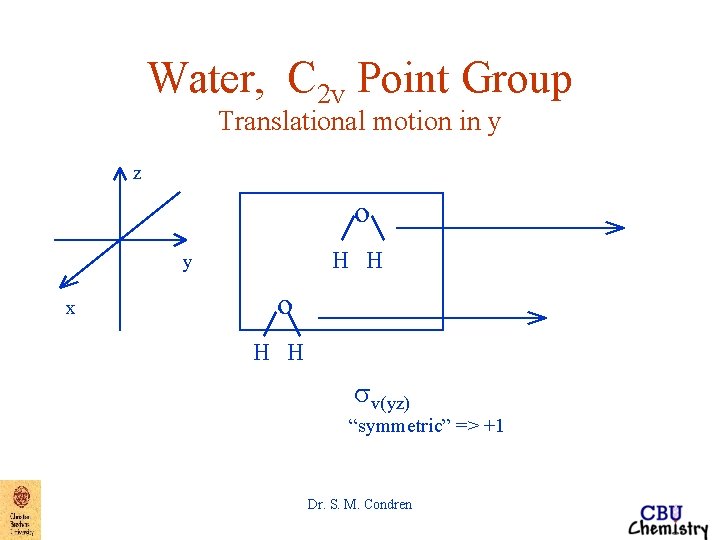
Water, C 2 v Point Group Translational motion in y z o H H y x o H H sv(yz) “symmetric” => +1 Dr. S. M. Condren

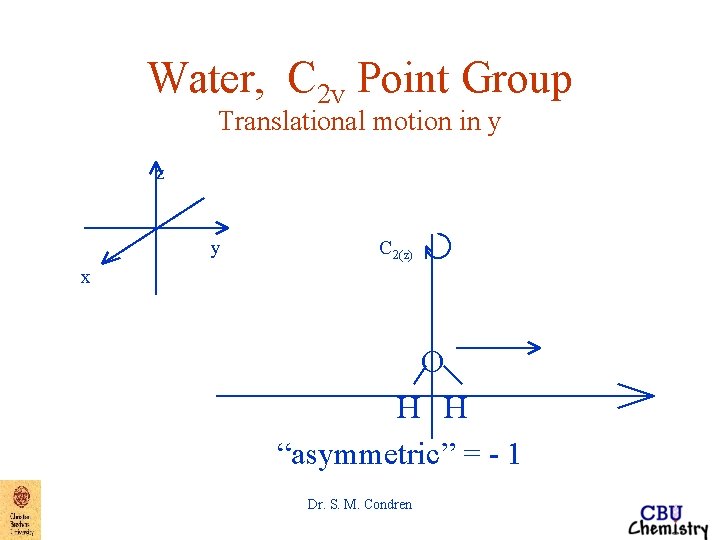
Water, C 2 v Point Group Translational motion in y z y C 2(z) x O H H “asymmetric” = - 1 Dr. S. M. Condren

Water, C 2 v Point Group Translational motion in y Representation: E C 2(z) G 3 +1 -1 Dr. S. M. Condren sv(xz) sv(yz) -1 +1

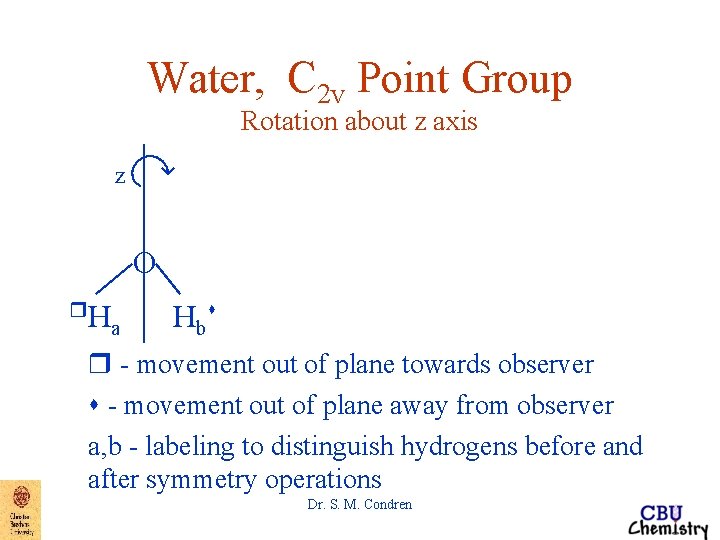
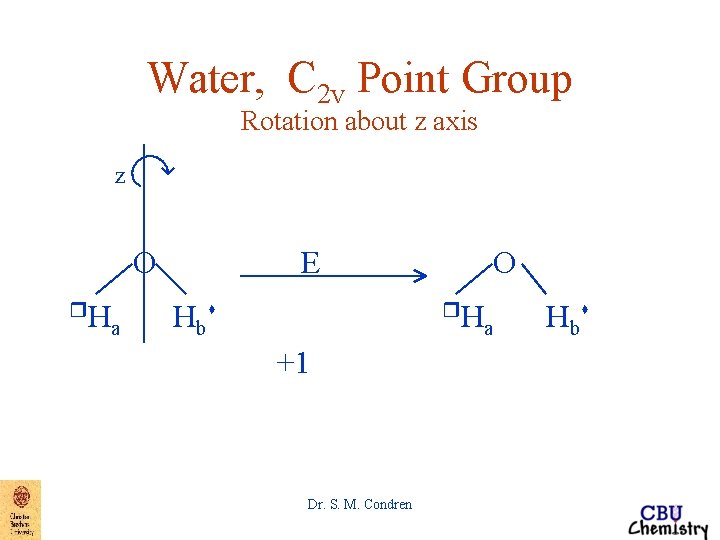
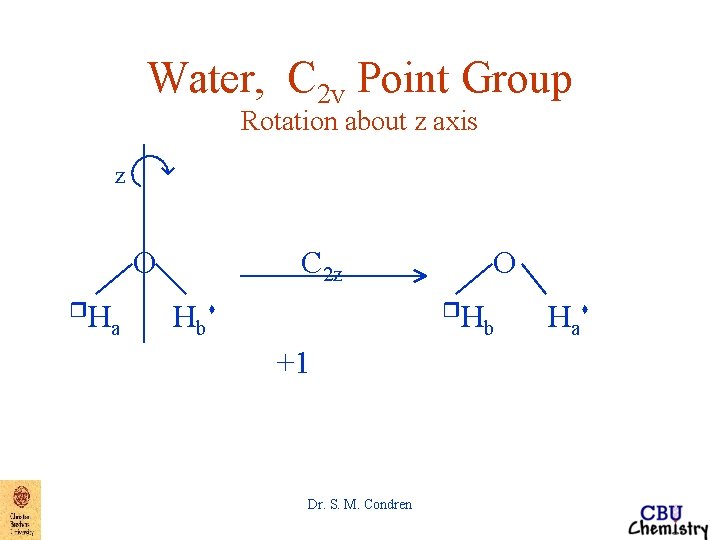
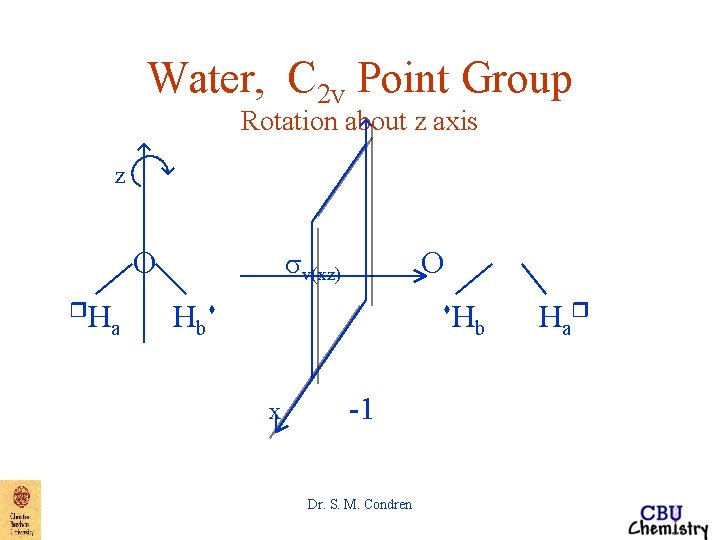
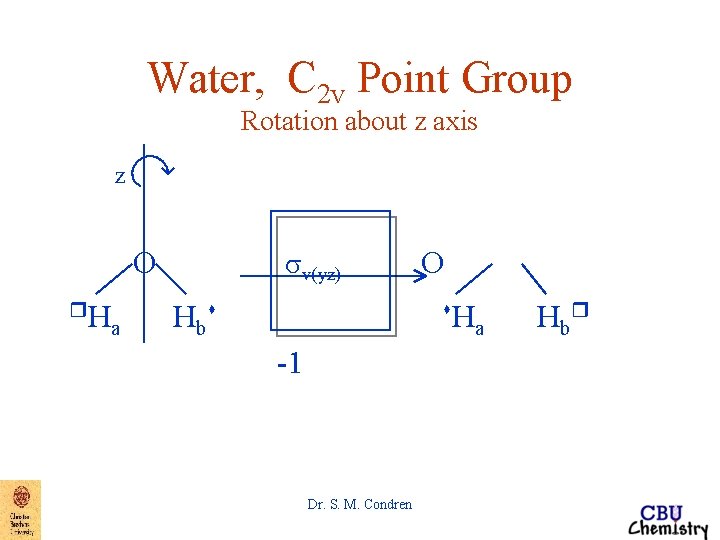
Water, C 2 v Point Group Rotation about z axis z O r. H a Hbs r - movement out of plane towards observer s - movement out of plane away from observer a, b - labeling to distinguish hydrogens before and after symmetry operations Dr. S. M. Condren

Water, C 2 v Point Group Rotation about z axis z O r. H a E Hbs O r. H +1 Dr. S. M. Condren a H bs

Water, C 2 v Point Group Rotation about z axis z O r. H a C 2 z Hbs O r. H +1 Dr. S. M. Condren b Ha s

Water, C 2 v Point Group Rotation about z axis z O r. H a O sv(xz) Hbs s. H x -1 Dr. S. M. Condren b Ha r

Water, C 2 v Point Group Rotation about z axis z O r. H a sv(yz) Hbs O s. H -1 Dr. S. M. Condren a Hbr

Water, C 2 v Point Group Rotation about z axis Representation E C 2(z) G 4 +1 +1 Dr. S. M. Condren sv(xz) sv(yz) -1 -1

Water, C 2 v Point Group Representations: Rotation E C 2(z) G 4 +1 +1 Dr. S. M. Condren sv(xz) sv(yz) -1 -1

Water, C 2 v Point Group Representation: Translation E C 2(z) G 1 +1 +1 G 2 +1 -1 G 3 +1 -1 sv(xz) sv(yz) +1 +1 Tz +1 -1 Tx -1 +1 Ty Dr. S. M. Condren

Water, C 2 v Point Group Representation: Rotation E C 2(z) G 4 +1 +1 G 5 +1 -1 G 6 +1 -1 sv(xz) sv(yz) -1 -1 Rz +1 -1 Ry -1 +1 Rx Dr. S. M. Condren

Water, C 2 v Point Group Character Table E C 2(z) A 1 +1 +1 A 2 +1 +1 B 1 +1 -1 B 2 +1 -1 sv(xz) sv(yz) +1 +1 -1 -1 +1 Dr. S. M. Condren Tz Rz R y, T x Rx, Ty G 1 G 4 G 2 , G 5 G 3, G 6

Dr. S. M. Condren

Vibrational Modes in CO 2 For linear molecules: 3 N - 5 IR fundamentals Dr. S. M. Condren

Vibrational Modes in SO 2 For non-linear molecules: 3 N - 6 IR fundamentals Dr. S. M. Condren

Vibration Modes for SO 3 For non-linear molecules: 3 N - 6 IR fundamentals Dr. S. M. Condren

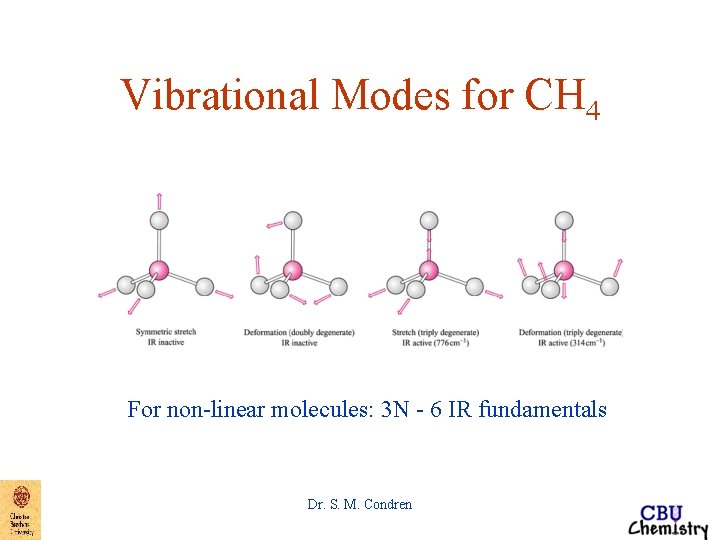
Vibrational Modes for CH 4 For non-linear molecules: 3 N - 6 IR fundamentals Dr. S. M. Condren

Vibrational Modes for [Pt. Cl 4]-2 For non-linear molecules: 3 N - 6 IR fundamentals Dr. S. M. Condren

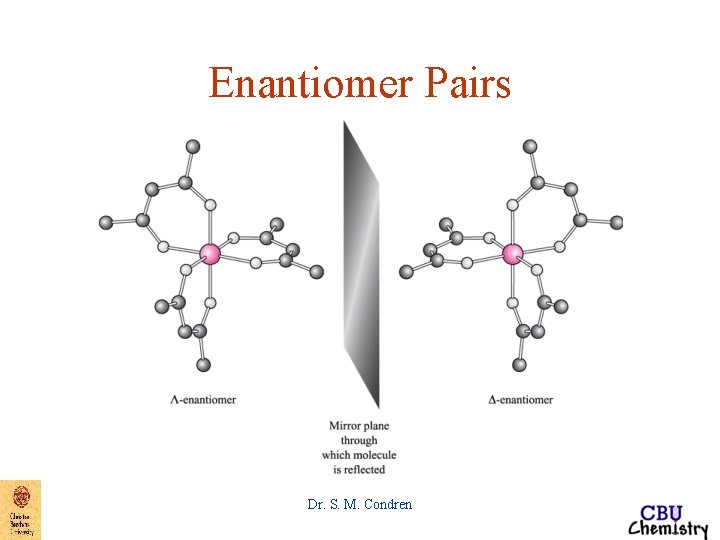
Enantiomer Pairs Dr. S. M. Condren

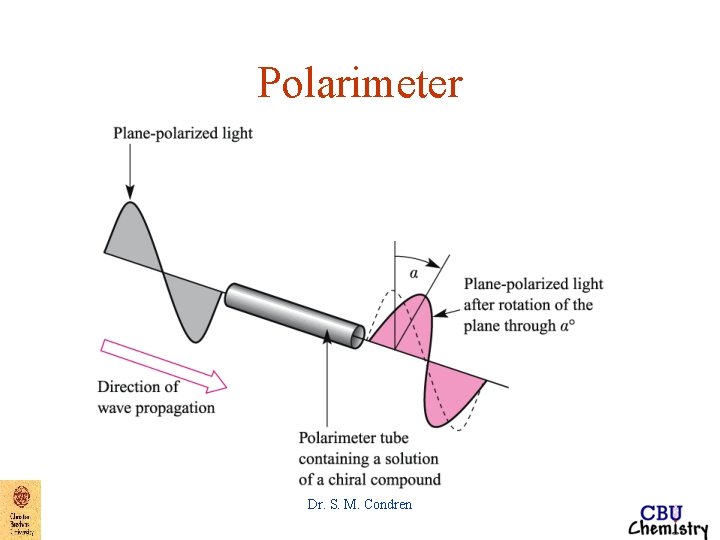
Polarimeter Dr. S. M. Condren