Chapter 4 Methods of Analysis of Resistive Circuits

Chapter 4 Methods of Analysis of Resistive Circuits Seokyeong University

Chapter 4 Methods of Analysis of Resistive Circuits Objectives n Increasingly complex circuits are required to meet the needs of ever-growing communication systems Ø As the complexity of circuits increased, analysis techniques were developed that incorporated rigorous systematic methods n We define and utilize two widely used methods of analysis Ø (1) node voltage and (2) mesh current analysis Ø These very powerful methods are widely used today for the analysis of large complex circuits in communications and electrical systems Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (I) n Node Voltage Analysis Ø It is customary to draw the elements horizontally or vertically and to connect these elements by horizontal and vertical lines that represents wires Node : place where the elements are connected together n Reference Node : a node selected as a reference from which a relative voltage is considered Ø any node can be selected to be the reference node Ø often choose the node at the bottom of the circuit to be the reference node Ø when the circuit contains a grounded power supply, the ground node at the power supply is usually selected as the reference node Seokyeoung University

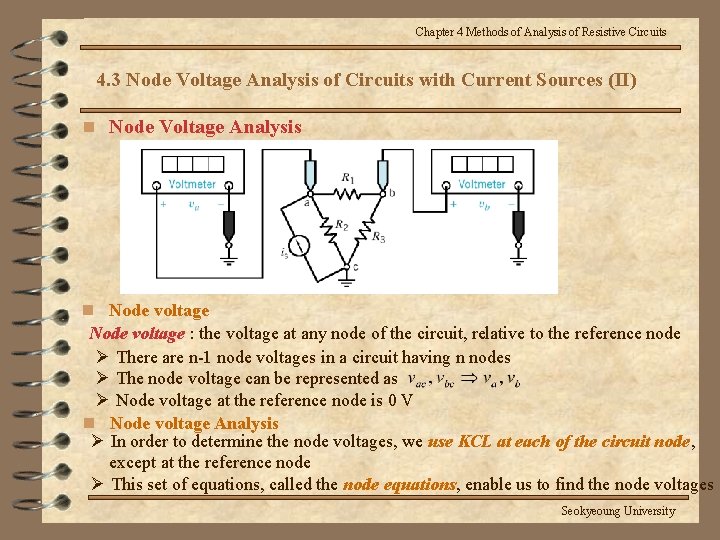
Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (II) n Node Voltage Analysis n Node voltage : the voltage at any node of the circuit, relative to the reference node Ø There are n-1 node voltages in a circuit having n nodes Ø The node voltage can be represented as Ø Node voltage at the reference node is 0 V n Node voltage Analysis Ø In order to determine the node voltages, we use KCL at each of the circuit node, except at the reference node Ø This set of equations, called the node equations, enable us to find the node voltages Seokyeoung University

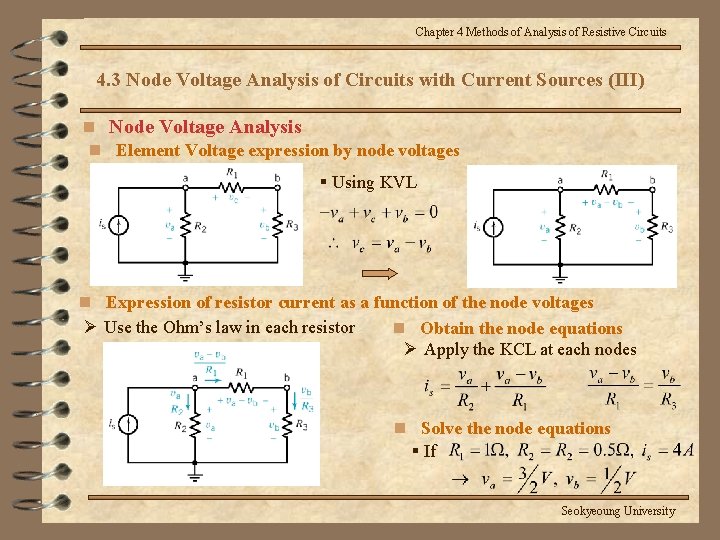
Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (III) n Node Voltage Analysis n Element Voltage expression by node voltages § Using KVL n Expression of resistor current as a function of the node voltages Ø Use the Ohm’s law in each resistor n Obtain the node equations Ø Apply the KCL at each nodes n Solve the node equations § If Seokyeoung University

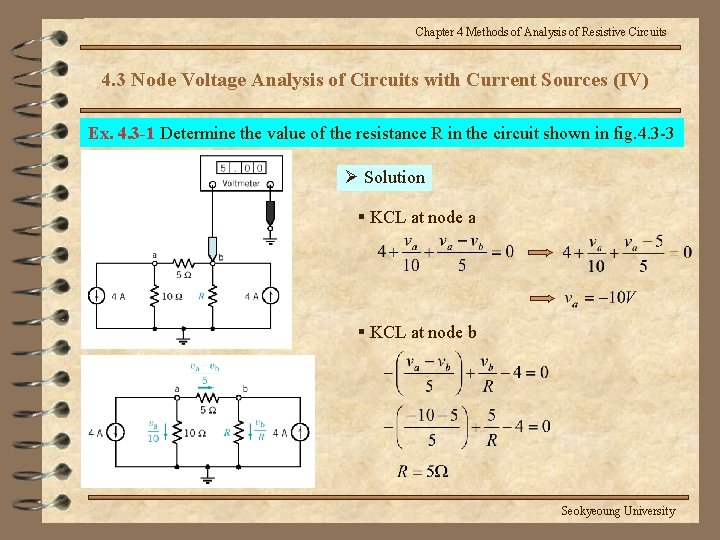
Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (IV) Ex. 4. 3 -1 Determine the value of the resistance R in the circuit shown in fig. 4. 3 -3 Ø Solution § KCL at node a § KCL at node b Seokyeoung University

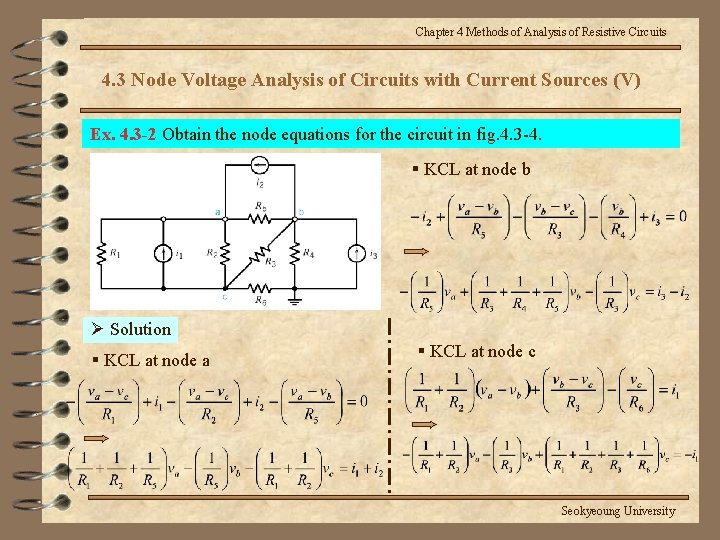
Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (V) Ex. 4. 3 -2 Obtain the node equations for the circuit in fig. 4. 3 -4. § KCL at node b Ø Solution § KCL at node a § KCL at node c Seokyeoung University

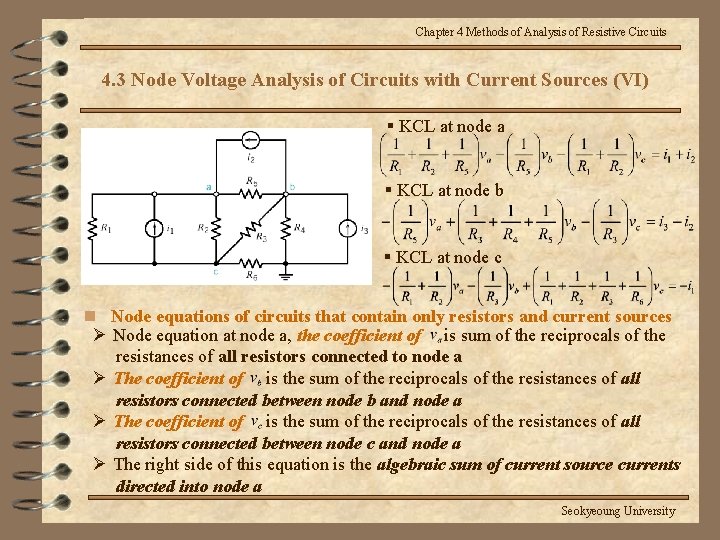
Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (VI) § KCL at node a § KCL at node b § KCL at node c n Node equations of circuits that contain only resistors and current sources Ø Node equation at node a, the coefficient of is sum of the reciprocals of the resistances of all resistors connected to node a Ø The coefficient of is the sum of the reciprocals of the resistances of all resistors connected between node b and node a Ø The coefficient of is the sum of the reciprocals of the resistances of all resistors connected between node c and node a Ø The right side of this equation is the algebraic sum of current source currents directed into node a Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 3 Node Voltage Analysis of Circuits with Current Sources (VII) Ex. 4. 3 -3 Determine the node voltages for the circuit in fig. 4. 3 -4 when Ø Solution Seokyeoung University

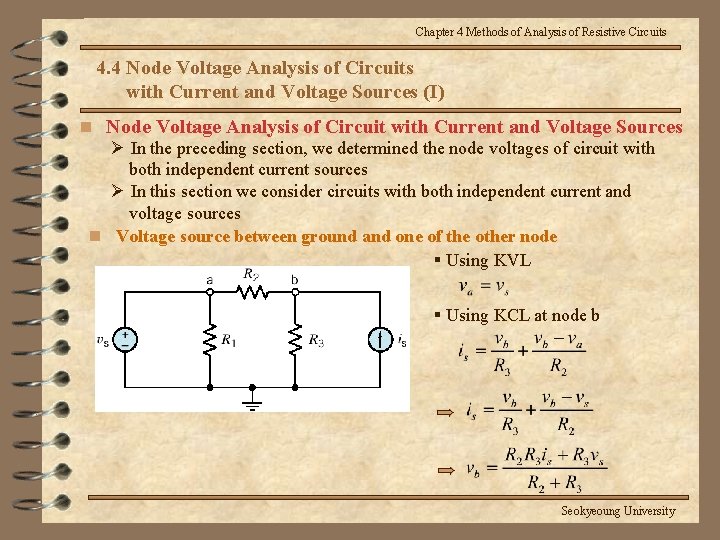
Chapter 4 Methods of Analysis of Resistive Circuits 4. 4 Node Voltage Analysis of Circuits with Current and Voltage Sources (I) n Node Voltage Analysis of Circuit with Current and Voltage Sources Ø In the preceding section, we determined the node voltages of circuit with both independent current sources Ø In this section we consider circuits with both independent current and voltage sources n Voltage source between ground and one of the other node § Using KVL § Using KCL at node b Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 4 Node Voltage Analysis of Circuits with Current and Voltage Sources (II) n Node Voltage Analysis of Circuit with Current and Voltage Sources n Voltage source between two nodes Ø We require a larger node since va and vb are dependent Ø The larger node often called a supernode or a generalized node § Using KVL § Using KCL at a supernode Seokyeoung University

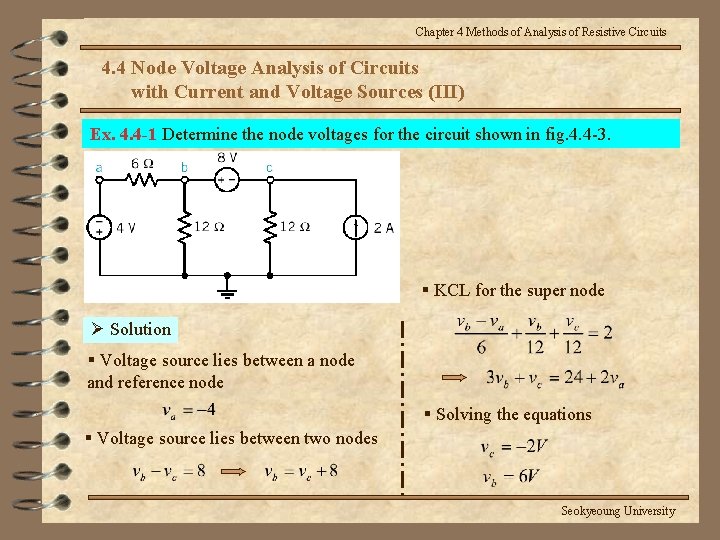
Chapter 4 Methods of Analysis of Resistive Circuits 4. 4 Node Voltage Analysis of Circuits with Current and Voltage Sources (III) Ex. 4. 4 -1 Determine the node voltages for the circuit shown in fig. 4. 4 -3. § KCL for the super node Ø Solution § Voltage source lies between a node and reference node § Solving the equations § Voltage source lies between two nodes Seokyeoung University

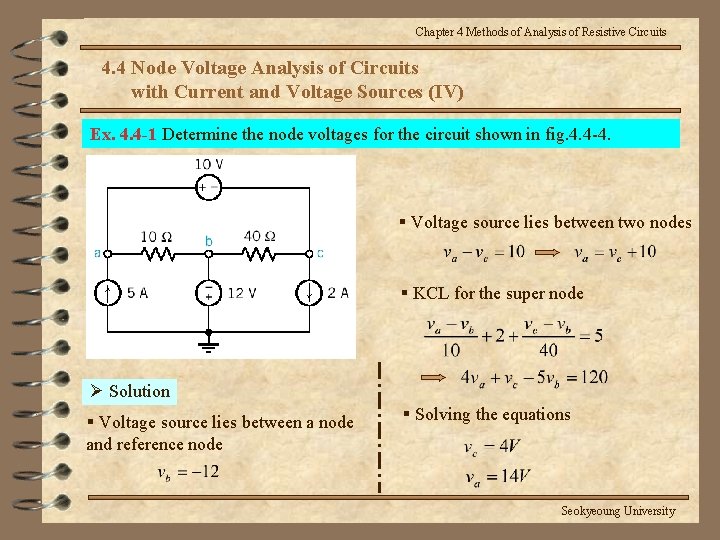
Chapter 4 Methods of Analysis of Resistive Circuits 4. 4 Node Voltage Analysis of Circuits with Current and Voltage Sources (IV) Ex. 4. 4 -1 Determine the node voltages for the circuit shown in fig. 4. 4 -4. § Voltage source lies between two nodes § KCL for the super node Ø Solution § Voltage source lies between a node and reference node § Solving the equations Seokyeoung University

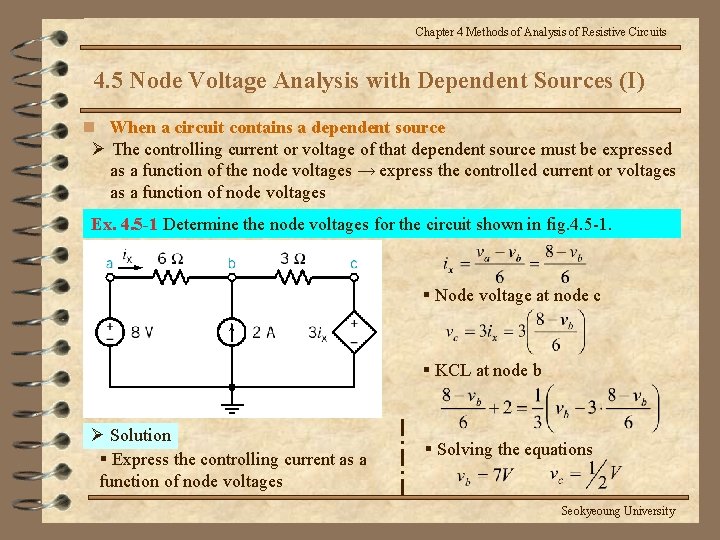
Chapter 4 Methods of Analysis of Resistive Circuits 4. 5 Node Voltage Analysis with Dependent Sources (I) n When a circuit contains a dependent source Ø The controlling current or voltage of that dependent source must be expressed as a function of the node voltages → express the controlled current or voltages as a function of node voltages Ex. 4. 5 -1 Determine the node voltages for the circuit shown in fig. 4. 5 -1. § Node voltage at node c § KCL at node b Ø Solution § Express the controlling current as a function of node voltages § Solving the equations Seokyeoung University

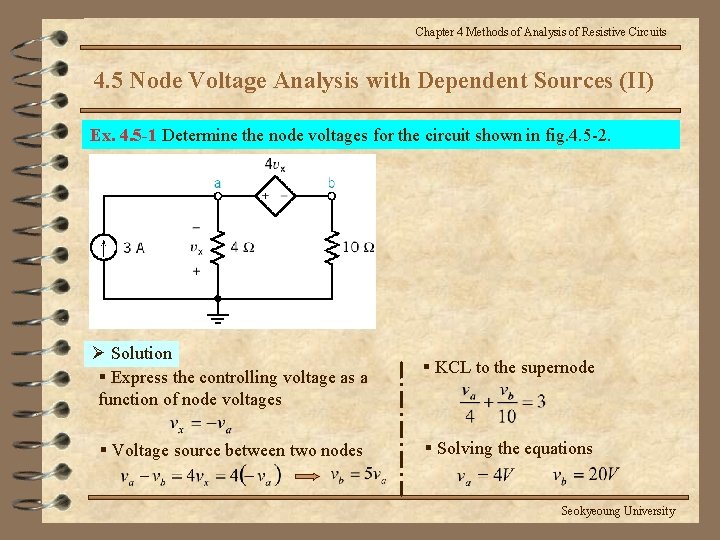
Chapter 4 Methods of Analysis of Resistive Circuits 4. 5 Node Voltage Analysis with Dependent Sources (II) Ex. 4. 5 -1 Determine the node voltages for the circuit shown in fig. 4. 5 -2. Ø Solution § Express the controlling voltage as a function of node voltages § KCL to the supernode § Voltage source between two nodes § Solving the equations Seokyeoung University

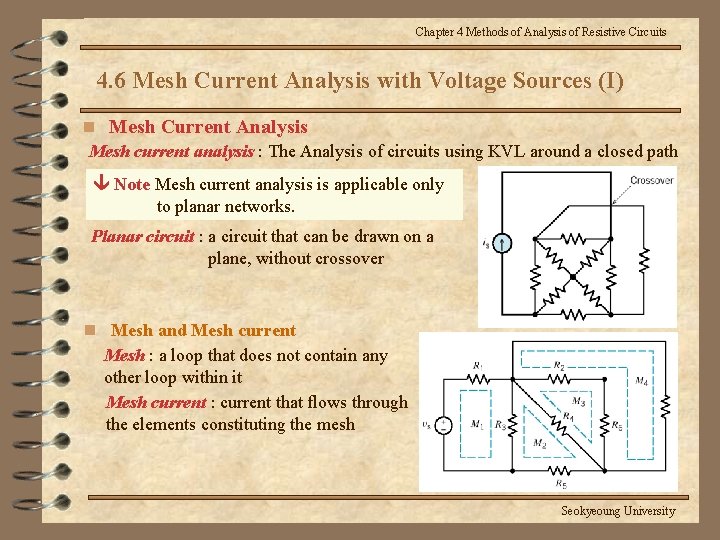
Chapter 4 Methods of Analysis of Resistive Circuits 4. 6 Mesh Current Analysis with Voltage Sources (I) n Mesh Current Analysis Mesh current analysis : The Analysis of circuits using KVL around a closed path Note Mesh current analysis is applicable only to planar networks. Planar circuit : a circuit that can be drawn on a plane, without crossover n Mesh and Mesh current Mesh : a loop that does not contain any other loop within it Mesh current : current that flows through the elements constituting the mesh Seokyeoung University

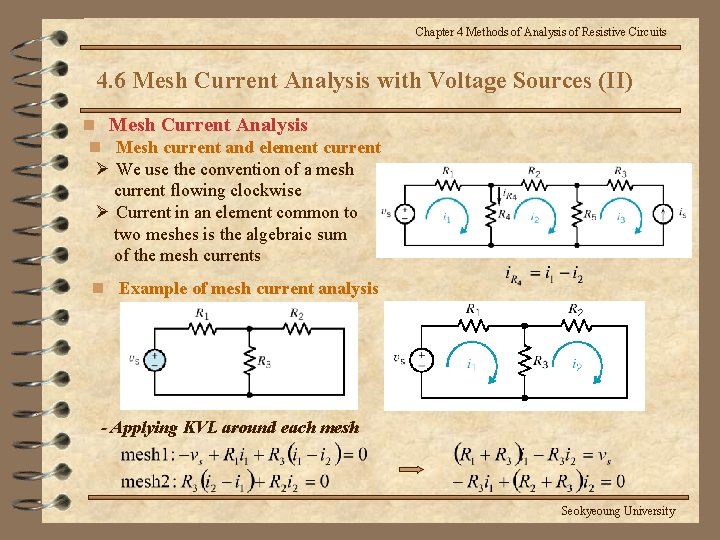
Chapter 4 Methods of Analysis of Resistive Circuits 4. 6 Mesh Current Analysis with Voltage Sources (II) n Mesh Current Analysis n Mesh current and element current Ø We use the convention of a mesh current flowing clockwise Ø Current in an element common to two meshes is the algebraic sum of the mesh currents n Example of mesh current analysis - Applying KVL around each mesh Seokyeoung University

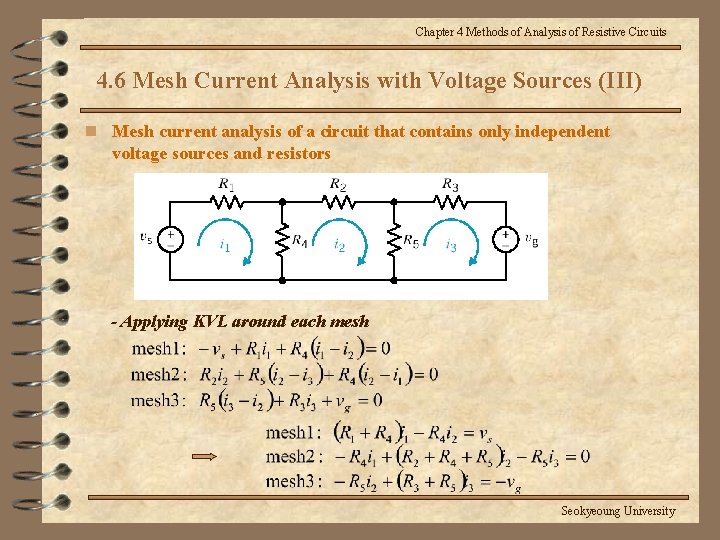
Chapter 4 Methods of Analysis of Resistive Circuits 4. 6 Mesh Current Analysis with Voltage Sources (III) n Mesh current analysis of a circuit that contains only independent voltage sources and resistors - Applying KVL around each mesh Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 6 Mesh Current Analysis with Voltage Sources (IV) n The equation for the nth mesh with independent voltage sources only Ø multiply by the sum of all resistances around the mesh Ø add the terms due to the resistances in common with another mesh as the negative of the connecting resistance , multiplied by the mesh current in the adjacent mesh for all adjacent meshes. Ø independent voltage sources around the loop appear on the right side of the equation as the negative of voltage source encountered as we traverse the loop in the direction of the mesh current Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 6 Mesh Current Analysis with Voltage Sources (V) n General matrix equation Ø a symmetric matrix Ø diagonal consisting of the sum of resistances in each mesh Ø off-diagonal elements are negative of sum of the resistances common to two meshes n Mesh equations of the matrix from for the circuit Seokyeoung University

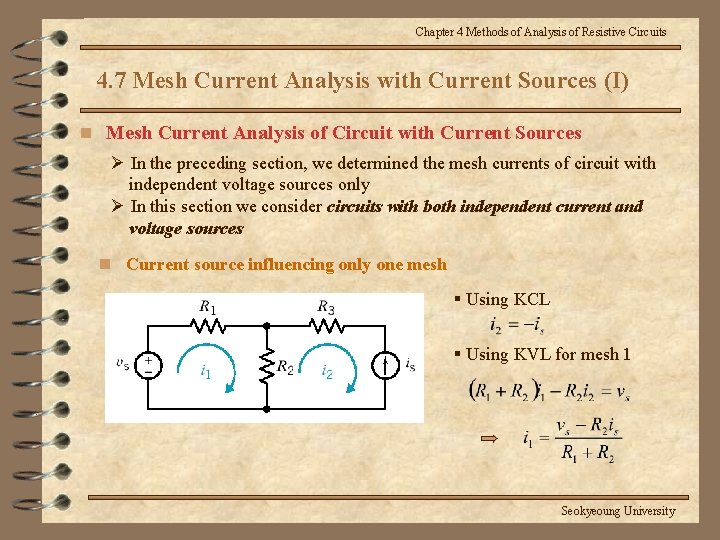
Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (I) n Mesh Current Analysis of Circuit with Current Sources Ø In the preceding section, we determined the mesh currents of circuit with independent voltage sources only Ø In this section we consider circuits with both independent current and voltage sources n Current source influencing only one mesh § Using KCL § Using KVL for mesh 1 Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (II) n Mesh Current Analysis of Circuit with Current Sources n Current source influencing two mesh currents (1) Ø Assume a voltage across the terminals of the current source Ø Write the KVL equations for both meshes Ø Add these two mesh equations → obtain an equation independent of § Using KCL at node a § Using KVL for both meshes § Adding two mesh equations Seokyeoung University

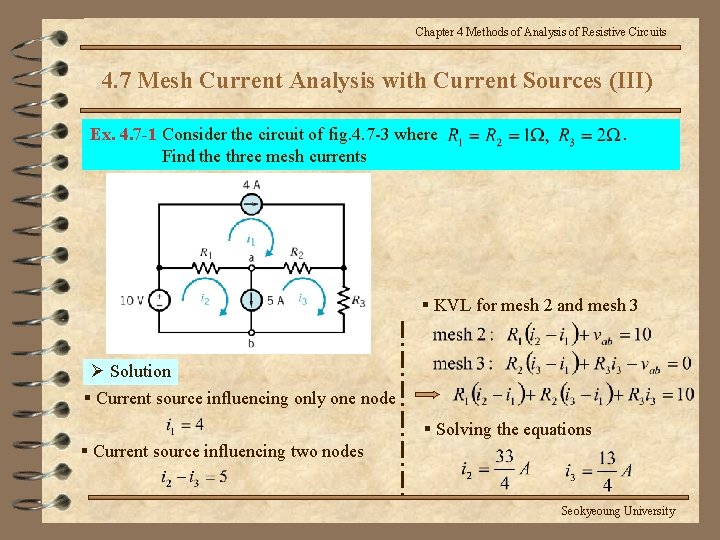
Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (III) Ex. 4. 7 -1 Consider the circuit of fig. 4. 7 -3 where Find the three mesh currents . § KVL for mesh 2 and mesh 3 Ø Solution § Current source influencing only one node § Solving the equations § Current source influencing two nodes Seokyeoung University

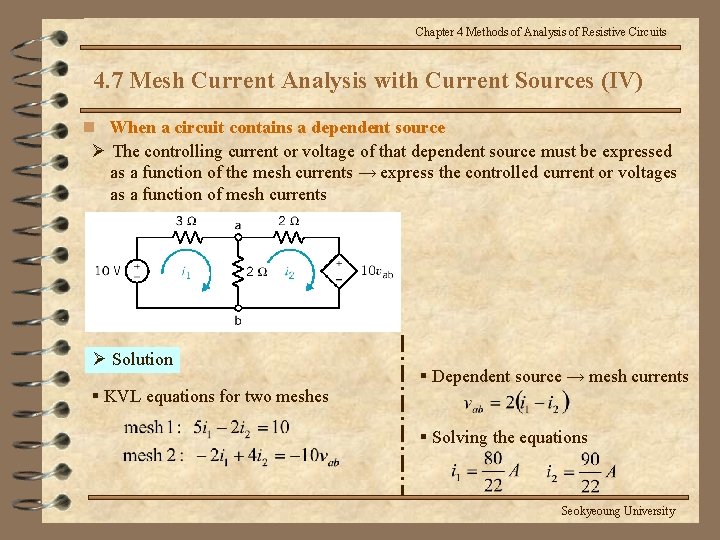
Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (IV) n When a circuit contains a dependent source Ø The controlling current or voltage of that dependent source must be expressed as a function of the mesh currents → express the controlled current or voltages as a function of mesh currents Ø Solution § KVL equations for two meshes § Dependent source → mesh currents § Solving the equations Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (V) n Mesh Current Analysis of Circuit with Current Sources n Current source influencing two mesh currents (2) – Using Supermesh : one larger mesh created from two meshes that have an independent or dependent current source in common Ø The common current source between two meshes reduces the number of independent mesh equations Ø One more constraint equation is derived from the common current source § Using KVL around the supermesh § Using KVL around the mesh 3 § Constraint equation by the current source Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (VI) n Mesh Current Analysis of Circuit with Current Sources Seokyeoung University

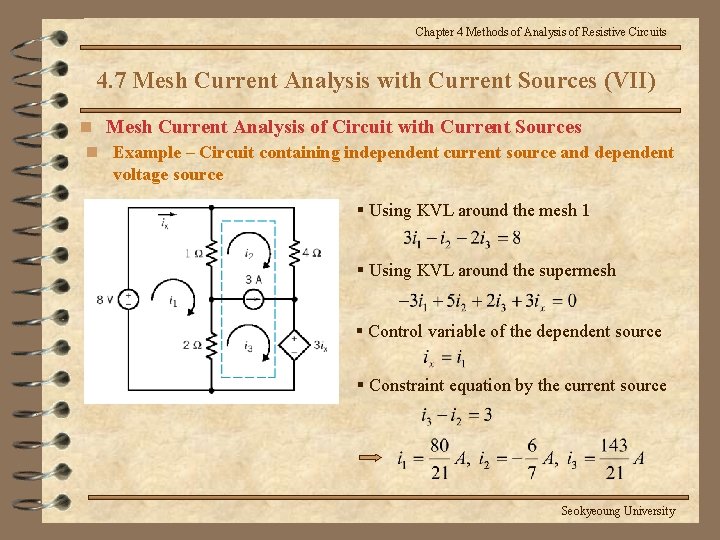
Chapter 4 Methods of Analysis of Resistive Circuits 4. 7 Mesh Current Analysis with Current Sources (VII) n Mesh Current Analysis of Circuit with Current Sources n Example – Circuit containing independent current source and dependent voltage source § Using KVL around the mesh 1 § Using KVL around the supermesh § Control variable of the dependent source § Constraint equation by the current source Seokyeoung University

Chapter 4 Methods of Analysis of Resistive Circuits 4. 8 The Node Voltage Method and Mesh Current Method Compared (I) n Node Voltage Analysis and Mesh Current Analysis Compared Ø Complex circuit needs systematic procedure to analyze Ø Node voltage method and mesh current method provide systematic procedure n What method is preferred over another Ø Circuit contains only voltage sources → Mesh current analysis Ø Circuit contains only current sources → Node voltage analysis Ø Circuit contains both current and voltage sources → (1) compare the number of equations (node, mesh) (2) what information is required (current, voltage) Seokyeoung University

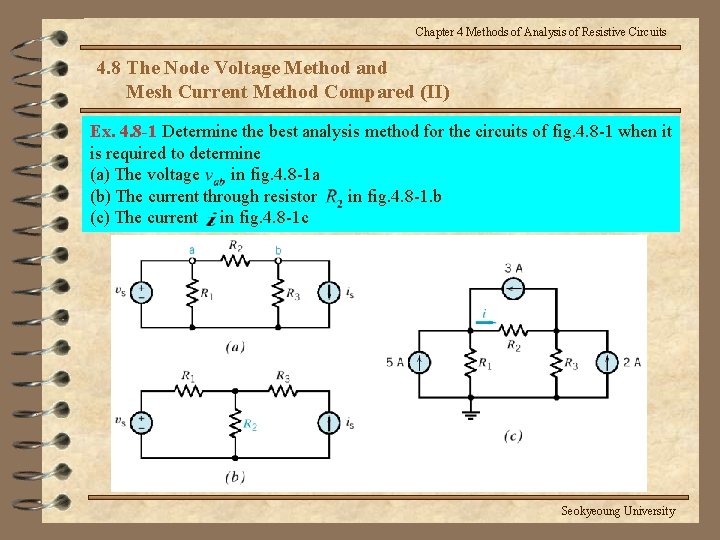
Chapter 4 Methods of Analysis of Resistive Circuits 4. 8 The Node Voltage Method and Mesh Current Method Compared (II) Ex. 4. 8 -1 Determine the best analysis method for the circuits of fig. 4. 8 -1 when it is required to determine (a) The voltage in fig. 4. 8 -1 a (b) The current through resistor in fig. 4. 8 -1. b (c) The current in fig. 4. 8 -1 c Seokyeoung University