Chapter 4 Linear Programming Models Example 4 1

Chapter 4 Linear Programming Models

Example 4. 1 – Advertising Model ► General Flakes Company advertises a lowfat breakfast cereal in a variety of 30 second television ads placed in a variety of television shows. ► The ads in different shows vary by cost and by the type of viewers they are likely to reach. § Viewers have been separated into six mutually exclusive categories. ► The rating service can supply information on

Ex. 4. 1(cont’d) - Advertising Model ► It wants to know how many ads to place on each of several television shows to obtain required exposures at minimum costs. ► This model is essentially the opposite of the product mix model. ► LP models ten to fall into “types” from a structural point of view, even though their actual contexts might be very different.

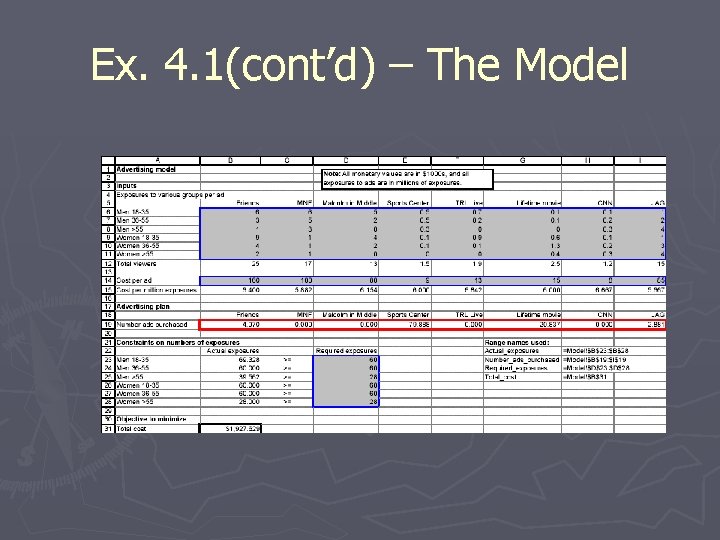
Ex. 4. 1(cont’d) – The Model

Ex. 4. 1(cont’d) – Developing the Model ► Follow these steps to develop the model: 1. Input values and range names. Enter the inputs given. 2. Ads purchased. Enter any values in the Number_ads_purchased range. 3. Exposures obtained. Enter the formula =SUMPRODUCT(B 6: I 6, Number_ads_purc hased) in cell B 23 and copy it down to cell B 28. 4. Total cost. In cell B 31 enter the formula =SUMPRODUCT(B 14: I 14, Number_ads_p urchased)

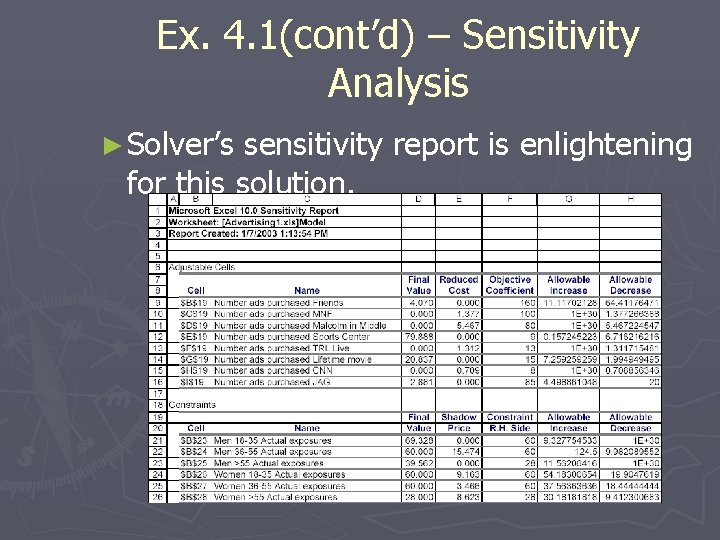
Ex. 4. 1(cont’d) – Sensitivity Analysis ► Solver’s sensitivity report is enlightening for this solution.

Ex. 4. 1(cont’d) – Dual Objective Extension of the Model ► General Flakes has two competing objectives 1. Obtain as many exposures as possible 2. Keep the total advertising cost as low as possible The original model minimized total cost and constrained the exposures to be at least as large as a required level. ► An alternative is to maximize the total number of excess exposures and put a ►

Ex. 4. 1(cont’d) – Dual Objective Extension of the Model ► To implement the alternative requires only minor modifications to the original. § Excess exposures. Enter the formula =B 23 D 23 in cell F 23. This cell becomes the new target cell to maximize. § Budget constraint. Calculate total cost but constrain it to be less than or equal to cell D 23. § Solver dialog box. Modify the Solver dialog box as shown.

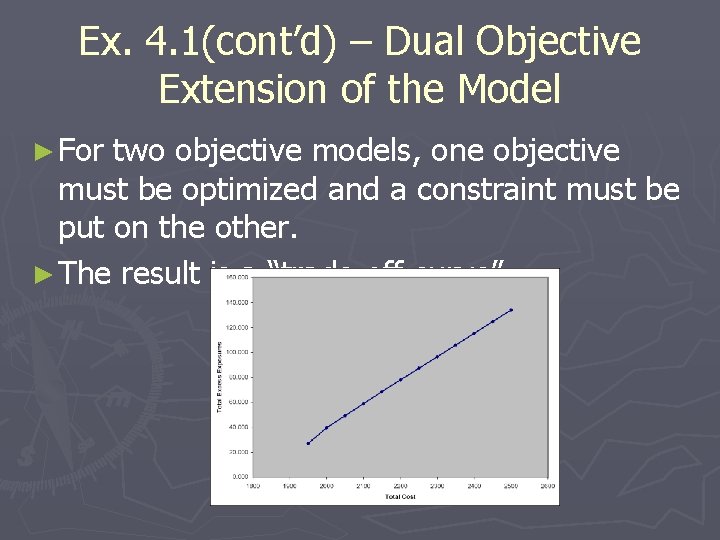
Ex. 4. 1(cont’d) – Dual Objective Extension of the Model ► For two objective models, one objective must be optimized and a constraint must be put on the other. ► The result is a “trade-off curve”.

Ex. 4. 1(cont’d) – Using Integer Constraints ► To force the changing cells to have integer values, you simply add another constraint in the Solver dialog box. ► Be aware that Solver must do a lot more work to solve problems with integer constraints.

Example 4. 2 – Static Workforce Model ►A post office requires different numbers of full-time employees on different days of the week. The number of full-time employees required each day is given. ► Union rules state that each full-time employee must work 5 consecutive days and then receive 2 days off. They only want to employ full-time employees. ► Its objective is to minimize the number of full-time employees that must be hired.

Ex. 4. 2 (cont’d) – The Solution ► In real employee scheduling problems much of the work involves forecasting and queuing analysis to obtain worker requirements. All of which must be done before any schedule optimizing. ► The key to this model is choosing the correct changing cells. ► The trick is to define to numbers of employees working each of the 7 possible 5 day shifts.

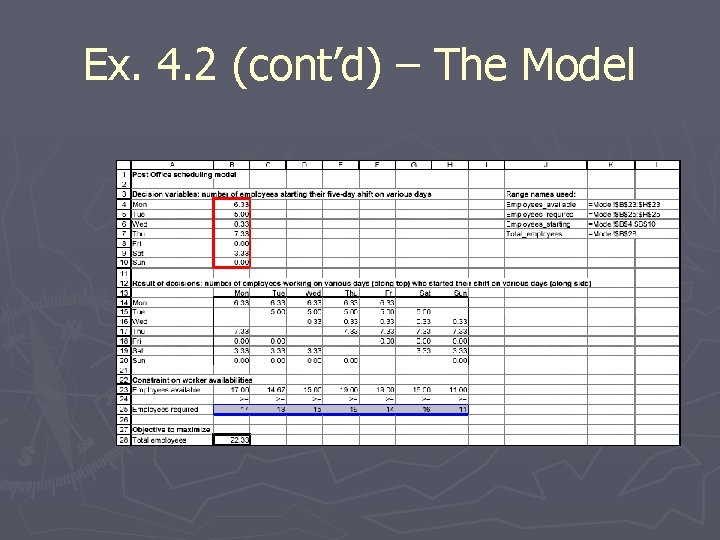
Ex. 4. 2 (cont’d) – The Model

Ex. 4. 2 (cont’d) – Developing the Model ► To form the spreadsheet, proceed as follows. 1. Inputs and range names. Enter the number of employees needed on each day of the week. 2. Employees beginning each day. Enter any trial values for the number of employees beginning work on each day in the Employee_starting range. 3. Employees on hand each day. Enter the formula =$B$4 in cell B 14 and copy it across to cell F 14. Proceed similarly for

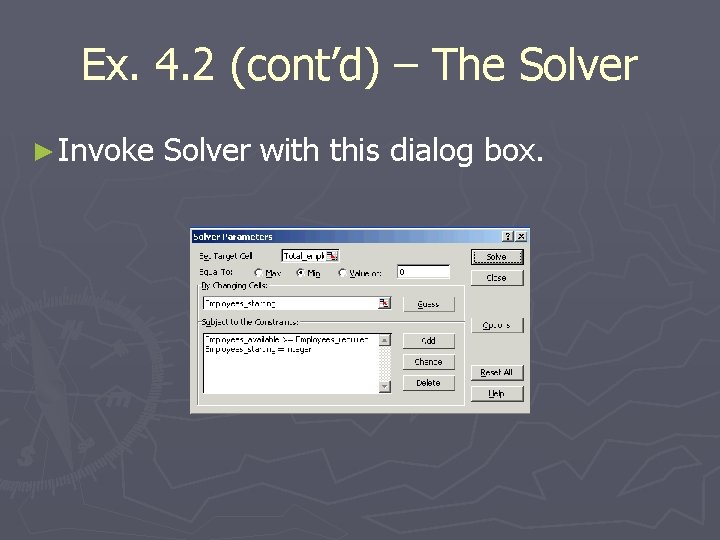
Ex. 4. 2 (cont’d) – The Solver ► Invoke Solver with this dialog box.

Ex. 4. 2 (cont’d) – The Solution ►A drawback is the number of employees starting work on some days is a fraction. § It’s simple to add an integer constraint on the changing cells. ► Set Solver’s Tolerance to 0 to ensure that you get the optimal solution.

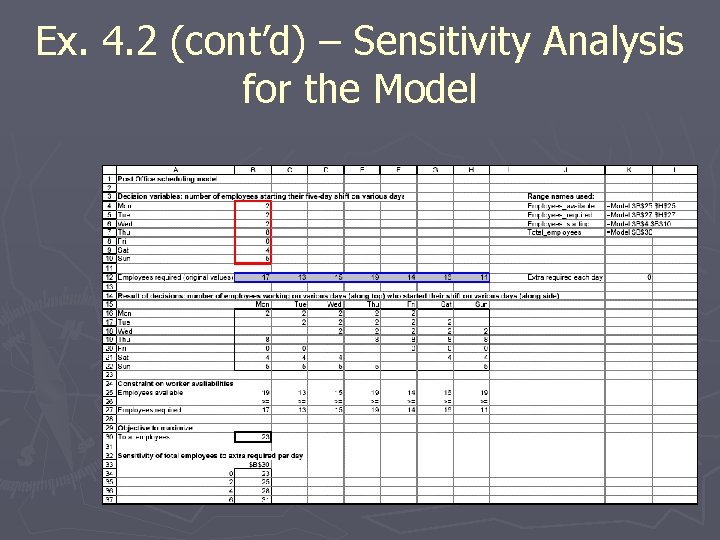
Ex. 4. 2 (cont’d) – Sensitivity Analysis ► How does the work schedule and the total number of employees change as the number of employees required each day changes? § Use Solver. Table after altering the model slightly. § Move the original requirements up to row 12, enter a trail value for the extra number required per day in cell K 12. § Enter the formula =B 12+$K$12 in cell B 27 and copy it across to H 27.

Ex. 4. 2 (cont’d) – Sensitivity Analysis for the Model

Ex. 4. 2 (cont’d) – Modeling Issues ► This type of problem dealt with what is called a static scheduling model, because it is assumed that the post office faces the same situation each week. ► In reality demands change and dynamic scheduling models are needed. ► In many scheduling models, heuristic methods (clever trial and error algorithms) can often be used. ► Heuristic solutions are often close to optimal, but they are never guaranteed to

Example 4. 3 – Aggregate Planning Model ► During the next four months the Sure. Step Company must meet (on time) the following demands for pairs of shoes. ► At the beginning of month 1, 500 pairs of shoes are on hand, and Sure. Step has 100 workers. ► A worker is paid $1, 500 per month. Each worker can work up to 160 hours a month before he or she receives

Ex. 4. 3 (cont’d) – Aggregate Planning Model ► It takes 4 hours of labor and $15 of raw material to produce a pair of shoes. ► At the beginning of each month workers can be hired or fired. Each hired worker costs $1600, and each fired worker cost $2000. ► At the end of each month, a holding cost of $3 per pair of shoes left in inventory is incurred. ► Sure. Step wants to us LP to determine

Ex. 4. 3 (cont’d) – The Solution ► Most difficult aspect is knowing which variables the company gets to choose and which are determined by these decisions. ► The company gets to choose § The number of workers to hire and fire. § The number of shoes to produce. § How many overtime hours to use within this limit. ► All the rest of the are determined.

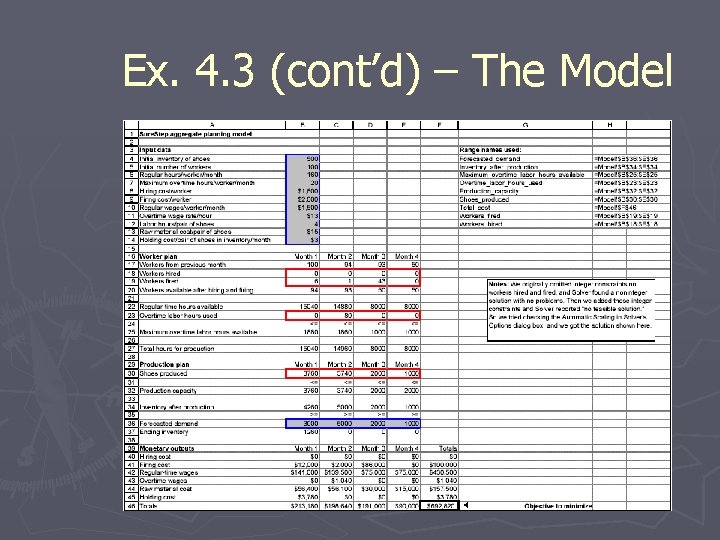
Ex. 4. 3 (cont’d) – The Model

Ex. 4. 3 (cont’d) – Developing the Model ► Developed as follows: § Inputs. Enter the input data in the range B 4: B 14 and in the Forecasted_demand range. § Production, hiring and firing plans. Enter any trial values for the number of pairs of shoes produced each month, the overtime hours used each month, the workers hired each month, and the workers fired each month. § Workers available each month. In cell B 17 enter the initial number of workers available with the formula =B 5. Because the number of workers available at the beginning of any other month is equal to the number of workers from the previous month, enter the formula =B 20 in cell C 17 and copy it to the range D 17: E 17.

Ex. 4. 3 (cont’d) – Developing the Model § Production capacity. Calculate the regular-time hours available in month 1 in cell B 22 with the formula =$B$6*B 20 and copy it to the range C 22: E 22 for the other months. Then calculate the total hours available for production in cell B 27 with the formula =SUM(B 22: B 23) and copy it to the range C 27: E 27. Calculate the production capacity for month 1 by entering the formula =B 27/$B$12 in cell B 32, and copy it to the range C 32: E 32. § Inventory each month. Enter the formula =B 4+B 30 in cell B 34.

Ex. 4. 3 (cont’d) – Developing the Model § Monthly costs. Calculate the various costs shown in rows 40 through 45 for month 1 by entering the formulas =$B$8*B 18 =$B$9*B 19 =$B$10*B 20 =$B$11*B 23 =$B$13*B 30 =$B$14*B 37

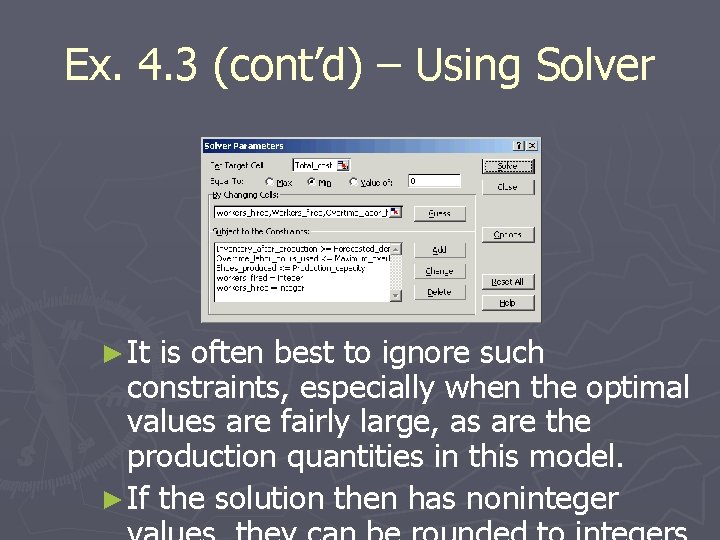
Ex. 4. 3 (cont’d) – Using Solver ► It is often best to ignore such constraints, especially when the optimal values are fairly large, as are the production quantities in this model. ► If the solution then has noninteger

Ex. 4. 3 (cont’d) –Solution & Sensitivity Analysis ► Because integer constraints make a model harder to solve, use them sparingly – only when they are really needed. ► To ensure that Solver finds the optimal solution in a problem where some or all of the changing cells must be integers, set the tolerance to 0. ► Many sensitivity analyses could be performed on this model.

Ex. 4. 3 (cont’d) – The Rolling Planning Horizon Approach ► Aggregate planning model is usually implemented via a rolling planning horizon. ► Sure. Step works with a 4 -month planning horizon. ► To implement the rolling planning horizon context, view the “demands” as forecasts and solve a 4 -month model with these forecasts.

Backlogging & Non. Smooth Functions ► The term “backlogging” means that the customer's demand will be met at a later date. § Backordering means the same thing. ► Formulas that contain IF functions accurately compute holding and shortage costs but they make the target cell a nonlinear function of the changing cells. ► When certain functions are used to relate the target cell to the changing cells, the resulting model becomes not

4. 5 Blending Models ► Linear programming can find the optimal combination of outputs as well as the “mix” of inputs that are used to produce the desired outputs. ► Blending models usually have various “quality” constraints, often expressed as required percentages of various ingredients. ► To keep these models linear (and avoid dividing by 0), it is important to “clear