Chapter 4 Linear Programming Applications in Marketing Finance

Chapter 4 Linear Programming Applications in Marketing, Finance, and Operations • Marketing Applications • Financial Applications • Operations Management Applications

Marketing Applications n Marketing Research • A firm conducts marketing research to learn about consumer characteristics, attitudes, and preferences. • Marketing research services include designing the study, conducting surveys, analyzing data collected, and providing recommendations for the client. • In the research design phase, targets or quotas may be established for the number and types of respondents to be surveyed. • The marketing research firm’s objective is to conduct the survey so as to meet the client’s needs at a minimum cost.

Marketing Research Market Survey, Inc. (MSI) specializes in evaluating consumer reaction to new products, services, and advertising campaigns. A client firm requested MSI’s assistance in ascertaining consumer reaction to a recently marketed household product. During meetings with the client, MSI agreed to conduct door-to-door personal interviews to obtain responses from households with children and households without children. In addition, MSI agreed to conduct both day and evening interviews.

Marketing Research The client’s contract called for MSI to conduct 1000 interviews under the following quota guidelines: 1. Interview at least 400 households with children. 2. Interview at least 400 households without children. 3. The total number of households interviewed during the evening must be at least as great as the number of households interviewed during the day. 4. At least 40% of the interviews for households with children must be conducted during the evening. 5. At least 60% of the interviews for households without children must be conducted during the evening.

Marketing Research Because the interviews for households with children take additional interviewer time and because evening interviewers are paid more than daytime interviewers, the cost varies with the type of interview. Based on previous research studies, estimates of the interview costs are as follows: Household Children No children Interview Cost Day Evening $20 $25 $18 $20

Marketing Research In formulating the linear programming model for the MSI problem, we utilize the following decision-variable notation: DC = the number of daytime interviews of households with children EC = the number of evening interviews of households with children DNC = the number of daytime interviews of households without children ENC = the number of evening interviews of households without children

Marketing Research The objective function: Min 20 DC + 25 EC + 18 DNC + 20 ENC The constraint requiring a total of 1000 interviews is: DC + EC + DNC + ENC = 1000 The specifications concerning the types of interviews: • Households with children: DC + EC > 400 • Households without children: DNC + ENC > 400 • At least as many evening interviews as day interviews EC + ENC > DC + DNC or -DC + EC - DNC + ENC > 0

Marketing Research The specifications concerning the types of interviews: • At least 40% of interviews of households with children during the evening: EC > 0. 4(DC + EC) or -0. 4 DC + 0. 6 EC > 0 • At least 60% of interviews of households without children during the evening: ENC > 0. 6(DNC + ENC) or -0. 6 DNC + 0. 4 ENC > 0 The non-negativity requirements: DC, EC, DNC, ENC > 0

Marketing Research The 4 -variable, 6 -constraint LP problem formulation is:

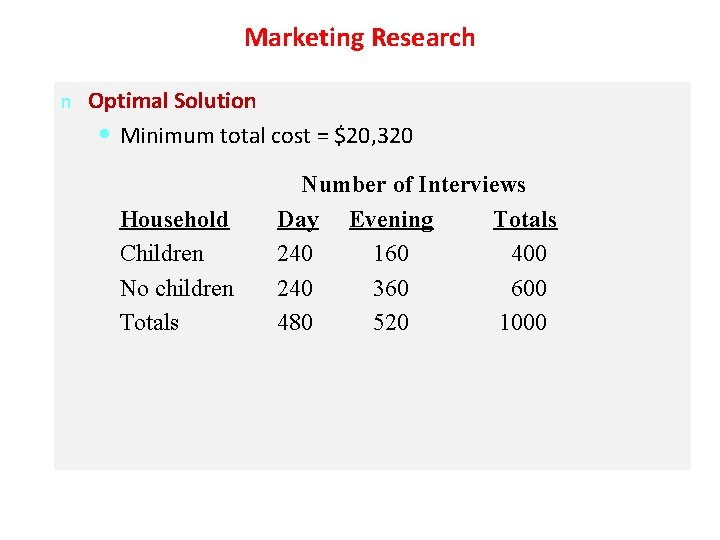
Marketing Research n Optimal Solution • Minimum total cost = $20, 320 Household Children No children Totals Number of Interviews Day Evening Totals 240 160 400 240 360 600 480 520 1000

Financial Applications n n n Portfolio selection problems involve choosing specific investments – for example, stocks and bonds – from a variety of investment alternatives. This type of problem is faced by managers of banks, mutual funds, and insurance companies. The objective function usually is maximization of expected return or minimization of risk.

Portfolio Selection Winslow Savings has $20 million available for investment. It wishes to invest over the next four months in such a way that it will maximize the total interest earned over the four month period as well as have at least $10 million available at the start of the fifth month for a high rise building venture in which it will be participating.

Portfolio Selection For the time being, Winslow wishes to invest only in 2 -month government bonds (earning 2% over the 2 -month period) and 3 -month construction loans (earning 6% over the 3 -month period). Each of these is available each month for investment. Funds not invested in these two investments are liquid and earn 3/4 of 1% per month when invested locally.

Portfolio Selection Formulate a linear program that will help Winslow Savings determine how to invest over the next four months if at no time does it wish to have more than $8 million in either government bonds or construction loans.

Portfolio Selection • Define the Decision Variables Gi = amount of new investment in government bonds in month i (for i = 1, 2, 3, 4) Ci = amount of new investment in construction loans in month i (for i = 1, 2, 3, 4) Li = amount invested locally in month i, (for i = 1, 2, 3, 4)

Portfolio Selection • Define the Objective Function Maximize total interest earned in the 4 -month period: Max (interest rate on investment) X (amount invested) Max. 02 G 1 +. 02 G 2 +. 02 G 3 +. 02 G 4 +. 06 C 1 +. 06 C 2 +. 06 C 3 +. 06 C 4 +. 0075 L 1 +. 0075 L 2 +. 0075 L 3 +. 0075 L 4

Portfolio Selection • Define the Constraints Month 1's total investment limited to $20 million: (1) G 1 + C 1 + L 1 = 20, 000 Month 2's total investment limited to principle and interest invested locally in Month 1: (2) G 2 + C 2 + L 2 = 1. 0075 L 1 or G 2 + C 2 - 1. 0075 L 1 + L 2 = 0

Portfolio Selection • Define the Constraints (continued) Month 3's total investment amount limited to principle and interest invested in government bonds in Month 1 and locally invested in Month 2: (3) G 3 + C 3 + L 3 = 1. 02 G 1 + 1. 0075 L 2 or - 1. 02 G 1 + G 3 + C 3 - 1. 0075 L 2 + L 3 = 0

Portfolio Selection • Define the Constraints (continued) Month 4's total investment limited to principle and interest invested in construction loans in Month 1, government bonds in Month 2, and locally invested in Month 3: (4) G 4 + C 4 + L 4 = 1. 06 C 1 + 1. 02 G 2 + 1. 0075 L 3 or - 1. 02 G 2 + G 4 - 1. 06 C 1 + C 4 - 1. 0075 L 3 + L 4 = 0 $10 million must be available at start of Month 5: (5) 1. 06 C 2 + 1. 02 G 3 + 1. 0075 L 4 > 10, 000

Portfolio Selection • Define the Constraints (continued) No more than $8 million in government bonds at any time: (6) G 1 < 8, 000 (7) G 1 + G 2 < 8, 000 (8) G 2 + G 3 < 8, 000 (9) G 3 + G 4 < 8, 000

Portfolio Selection • Define the Constraints (continued) No more than $8 million in construction loans at any time: (10) C 1 < 8, 000 (11) C 1 + C 2 < 8, 000 (12) C 1 + C 2 + C 3 < 8, 000 (13) C 2 + C 3 + C 4 < 8, 000 Non-negativity: Gi, Ci, Li > 0 for i = 1, 2, 3, 4

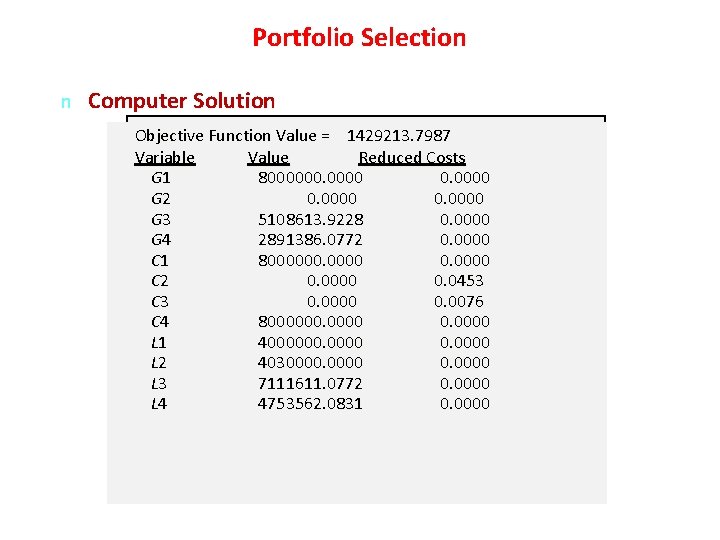
Portfolio Selection n Computer Solution Objective Function Value = 1429213. 7987 Variable Value Reduced Costs G 1 8000000 G 2 0. 0000 G 3 5108613. 9228 0. 0000 G 4 2891386. 0772 0. 0000 C 1 8000000 C 2 0. 0000 0. 0453 C 3 0. 0000 0. 0076 C 4 8000000 L 1 4000000 L 2 4030000 L 3 7111611. 0772 0. 0000 L 4 4753562. 0831 0. 0000

Operations Management Applications Make-or-buy decision Tots Toys makes a plastic tricycle that is composed of three major components: a handlebar-front wheel-pedal assembly, a seat and frame unit, and rear wheels. The company has orders for 12, 000 of these tricycles. Current schedules yield the following information. Requirements Cost to Component Plastic Time Space Manufacture Front 3 10 2 8 Seat/Frame 4 6 2 6 Rear wheel. 5 2. 1 1 (each) Available 50000 160000 30000 Cost to Purchase 12 9 3

The company obviously does not have the resources available to manufacture everything needed for the completion of 12000 tricycles so has gathered purchase information for each component. Develop a linear programming model to tell the company how many of each component should be manufactured and how many should be purchased in order to provide 12000 fully completed tricycles at the minimum cost.

ANS : Let: FM = number of fronts made SM = number of seats made WM = number of wheels made FP = number of fronts purchased SP = number of seats purchased WP = number of wheels purchased

Min 8 FM + 6 SM + 1 WM + 12 FP + 9 SP + 3 WP s. t. 3 FM + 4 SM +. 5 WM £ 50000 10 FM + 6 SM + 2 WM £ 160000 2 FM + 2 SM +. 1 WM £ 30000 FM + FP ³ 12000 SM + SP ³ 12000 WM + WP ³ 24000 FM, SM, WM, FP, SP, WP ³ 0