Chapter 4 Lecture Circular Motion Gravity and Planets

Chapter 4 Lecture Circular Motion Gravity and Planets © 2014 Pearson Education, Inc.

Observations and explanations of planetary motion • Newton was among the first to hypothesize that the Moon moves in a circular orbit around Earth because Earth pulls on it, continuously changing the direction of the Moon's velocity. • He wondered if the force exerted by Earth on the Moon was the same type of force that Earth exerted on falling objects, such as an apple falling from a tree. © 2014 Pearson Education, Inc.

Observations and explanations of planetary motion • Newton compared the acceleration of the Moon if it could be modeled as a point particle near Earth's surface to the acceleration of the moon observed in its orbit: © 2014 Pearson Education, Inc.

Observations and explanations of planetary motion (Cont'd) © 2014 Pearson Education, Inc.

Tip • You might wonder why if Earth pulls on the Moon, the Moon does not come closer to Earth in the same way that an apple falls from a tree. • The difference in these two cases is the speed of the objects. The apple is at rest with respect to Earth before it leaves the tree, and the Moon is moving tangentially. • If Earth stopped pulling on the Moon, it would fly away along a straight line. © 2014 Pearson Education, Inc.

Dependence of gravitational force on mass • Newton deduced by recognizing that acceleration would equal g only if the gravitational force was directly proportional to the system object's mass. • Newton deduced by applying the third law of motion. © 2014 Pearson Education, Inc.

The law of universal gravitation • Newton deduced but did not know the proportionality constant; in fact, at that time the mass of the Moon and Earth were unknown. • Later scientists determined the proportionality: • G is the universal gravitational constant, indicating that this law works anywhere in the universe for any two masses. © 2014 Pearson Education, Inc.

The universal gravitational constant • G is very small. • For two objects of mass 1 kg that are separated by 1 m, the gravitational force they exert on each other equals 6. 67 x 10– 11 N. • The gravitational force between everyday objects is small enough to ignore in most calculations. © 2014 Pearson Education, Inc.

Newton's law of universal gravitation © 2014 Pearson Education, Inc.

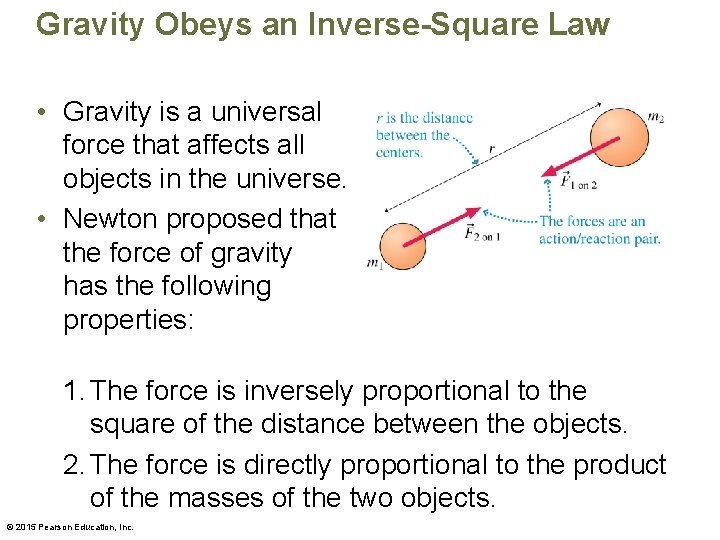
Gravity Obeys an Inverse-Square Law • Gravity is a universal force that affects all objects in the universe. • Newton proposed that the force of gravity has the following properties: 1. The force is inversely proportional to the square of the distance between the objects. 2. The force is directly proportional to the product of the masses of the two objects. © 2015 Pearson Education, Inc.

Making sense of the gravitational force that everyday objects exert on Earth • It might seem counterintuitive that objects exert a gravitational force on Earth; Earth does not seem to react every time someone drops something. • Acceleration is force divided by mass, and the mass of Earth is very large, so Earth's acceleration is very small. • For example, the acceleration caused by the gravitational force a tennis ball exerts on Earth is 9. 2 x 10– 26 m/s 2. © 2014 Pearson Education, Inc.

Free-fall acceleration • We can now understand why free-fall acceleration on Earth equals 9. 8 m/s 2. • This agrees with what we measure, providing a consistency check that serves the purpose of a testing experiment. © 2014 Pearson Education, Inc.

Making sense of the gravitational force that everyday objects exert on Earth • It might seem counterintuitive that objects exert a gravitational force on Earth; Earth does not seem to react every time someone drops something. • Acceleration is force divided by mass, and the mass of Earth is very large, so Earth's acceleration is very small. • For example, the acceleration caused by the gravitational force a tennis ball exerts on Earth is 9. 2 x 10– 26 m/s 2. © 2014 Pearson Education, Inc.

Kepler's laws and the law of universal gravitation • About 50 years before Newton's work, Johannes Kepler (1571– 1630) crafted his three laws of planetary motion. • Newton used the law of universal gravitation to explain Kepler's laws. • This work contributed to scientists' confidence in the law of universal gravitation. © 2014 Pearson Education, Inc.

Kepler's first law of planetary motion • The orbits of all planets are ellipses, with the Sun located at one of the ellipse's foci. • The shape of the planetary orbits is close to circular for most planets. In those cases, the foci of the ellipse are very close to the center of the circular orbit that most closely approximates the ellipse. © 2014 Pearson Education, Inc.

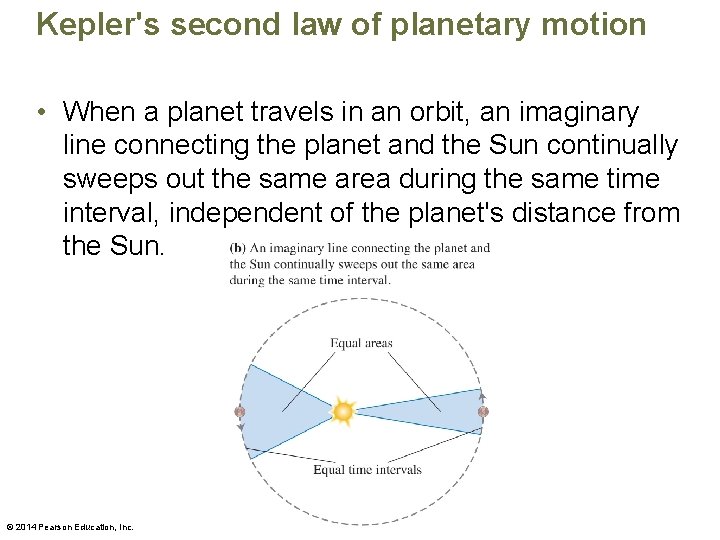
Kepler's second law of planetary motion • When a planet travels in an orbit, an imaginary line connecting the planet and the Sun continually sweeps out the same area during the same time interval, independent of the planet's distance from the Sun. © 2014 Pearson Education, Inc.

Kepler's third law of planetary motion • The square of the period T of the planet's motion (the time interval to complete one orbit) divided by the cube of the semi-major axis of the orbit (which is half the maximum diameter of the elliptical orbit and the radius r of a circle) equals the same constant for all the known planets: © 2014 Pearson Education, Inc.

Limitations of the law of universal gravitation • Even with calculus, the law cannot account for the details of some motions. • When astronomers made careful observations of the orbit of Mercury, they noticed that its orbit exhibited some patterns that the law of universal gravitation could not explain. • It was not until the early 20 th century, when Einstein constructed a more advanced theory of gravity, that scientists could predict all of the details of the motion of Mercury. © 2014 Pearson Education, Inc.

Circular Orbits and Weightlessness © 2014 Pearson Education, Inc.

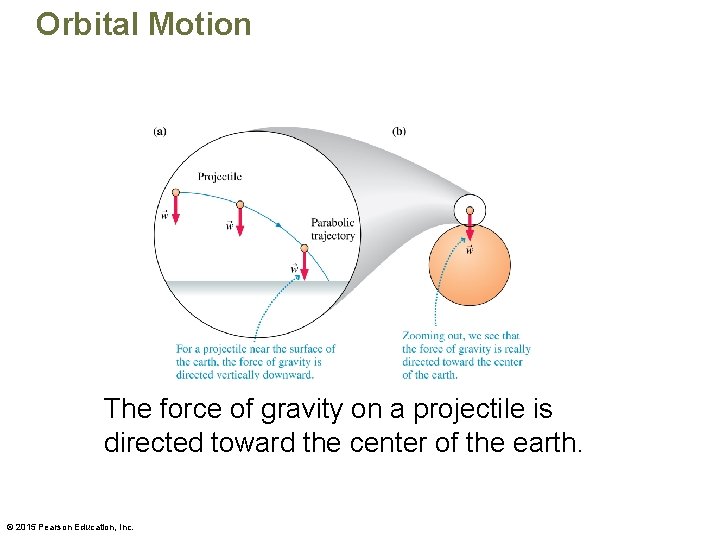
Orbital Motion The force of gravity on a projectile is directed toward the center of the earth. © 2015 Pearson Education, Inc.

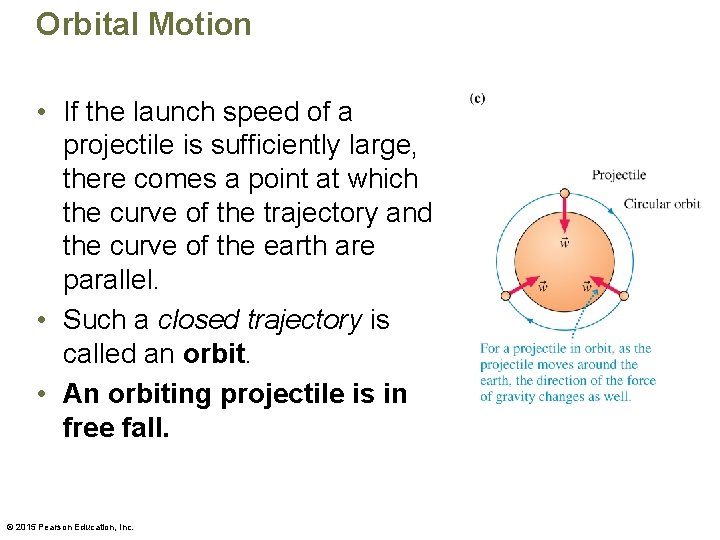
Orbital Motion • If the launch speed of a projectile is sufficiently large, there comes a point at which the curve of the trajectory and the curve of the earth are parallel. • Such a closed trajectory is called an orbit. • An orbiting projectile is in free fall. © 2015 Pearson Education, Inc.

Orbital Motion • The force of gravity is the force that causes the centripetal acceleration of an orbiting object: • An object moving in a circle of radius r at speed vorbit will have this centripetal acceleration if • That is, if object moves parallel (in orbit) to the surface of an object with speed • (This is also the speed at which apparent weightlessness will occur n=mg) © 2015 Pearson Education, Inc.

Orbital Motion: A couple of Definitions and Reminders • Apparent Weight: the upward force (normal force) that opposes a supported object from falling (What a scale reads) • Object True Weight: Force exerted by gravity or mg. • Wapparent = Actual Weight except: • Object has acceleration with a vertical component (i. e y direction) • Some force other than earth’s gravity is acting on the object: Normal, Magnetic, buoyant, centripetal or gravitational force of another body • Free Fall: A free falling object is an object that is falling at g. There are two important motion characteristics that are true of free-falling objects……….

Orbital Motion: A couple of Definitions and Reminders •

Orbital Motion • © 2015 Pearson Education, Inc.

Question 1 • Astronauts on the International Space Station are weightless because – There’s no gravity in outer space. – The net force on them is zero. – The centrifugal force balances the gravitational force. – g is very small, although not zero. – They are in free fall. © 2015 Pearson Education, Inc.

Question 1 • Astronauts on the International Space Station are weightless because – There’s no gravity in outer space. – The net force on them is zero. – The centrifugal force balances the gravitational force. – g is very small, although not zero. – They are in free fall. © 2015 Pearson Education, Inc.

Question: Gravitational force between two people You are seated in your physics class next to another student 0. 60 m away. Estimate the magnitude of the gravitational force between you. Assume that you each have a mass of 65 kg. © 2015 Pearson Education, Inc.

Question: Gravitational force between two people (cont. ) SOLVE The gravitational force is given by: The force is quite small, roughly the weight of one hair on your head. This seems reasonable; you don’t normally sense this attractive force! ASSESS © 2015 Pearson Education, Inc.

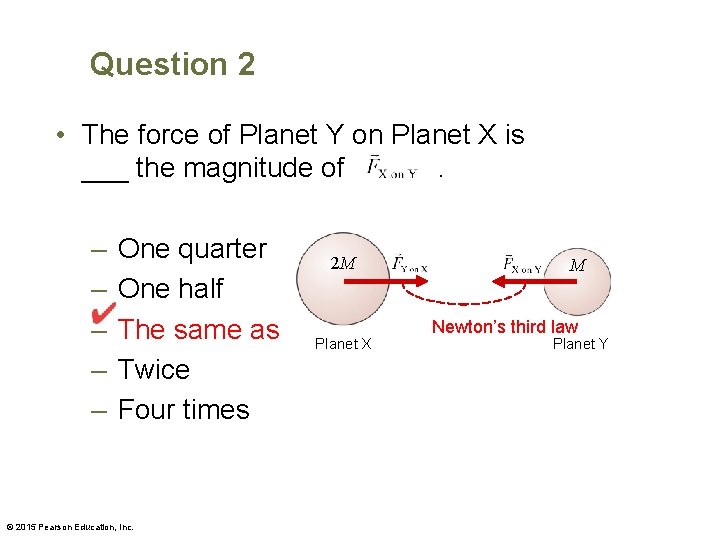
Question 2 • The force of Planet Y on Planet X is ___ the magnitude of. – – – One quarter One half The same as Twice Four times © 2015 Pearson Education, Inc. 2 M M Planet X Planet Y

Question 2 • The force of Planet Y on Planet X is ___ the magnitude of. – – – One quarter One half The same as Twice Four times © 2015 Pearson Education, Inc. 2 M Planet X M Newton’s third law Planet Y

Question 3 • The gravitational force between two asteroids is 1, 000 N. What will the force be if the distance between the asteroids is doubled? – 250, 000 N – 500, 000 N – 1, 000 N – 2, 000 N – 4, 000 N © 2015 Pearson Education, Inc.

Question 3 • The gravitational force between two asteroids is 1, 000 N. What will the force be if the distance between the asteroids is doubled? – 250, 000 N – 500, 000 N – 1, 000 N – 2, 000 N – 4, 000 N © 2015 Pearson Education, Inc.

Gravity on Other Worlds • If you traveled to another planet, your mass would be the same but your weight would vary. The weight of a mass m on the moon is given by • Using Newton’s law of gravity the weight is given by: • Since these are two expressions for the same force, they are equal and © 2015 Pearson Education, Inc.

Gravity on Other Worlds • If we use values for the mass and the radius of the moon, we compute gmoon = 1. 62 m/s 2. • A 70 -kg astronaut wearing an 80 -kg spacesuit would weigh more than 330 lb on the earth but only 54 lb on the moon. © 2015 Pearson Education, Inc.

Question 4 • Planet X has free-fall acceleration 8 m/s 2 at the surface. Planet Y has twice the mass and twice the radius of planet X. On Planet Y – – – g = 2 m/s 2 g = 4 m/s 2 g = 8 m/s 2 g = 16 m/s 2 g = 32 m/s 2 © 2015 Pearson Education, Inc.

Question 4 • Planet X has free-fall acceleration 8 m/s 2 at the surface. Planet Y has twice the mass and twice the radius of planet X. On Planet Y – – – g = 2 m/s 2 g = 4 m/s 2 g = 8 m/s 2 g = 16 m/s 2 g = 32 m/s 2 © 2015 Pearson Education, Inc.

Question 5 • A 60 -kg person stands on each of the following planets. On which planet is his or her weight the greatest? © 2015 Pearson Education, Inc.

Question 5 • A 60 -kg person stands on each of the following planets. On which planet is his or her weight the greatest? A © 2015 Pearson Education, Inc.

Question 6 Finding the speed to orbit Deimos Mars has two moons, each much smaller than the earth’s moon. The smaller of these two bodies, Deimos, isn’t quite spherical, but we can model it as a sphere of radius 6. 3 km. Its mass is 1. 8 × 1015 kg. At what speed would a projectile move in a very low orbit around Deimos? © 2015 Pearson Education, Inc.

Question 6: Finding the speed to orbit Deimos (cont. ) The free-fall acceleration at the surface of Deimos is small: SOLVE © 2015 Pearson Education, Inc.

Question 6: Finding the speed to orbit Deimos (cont. ) Given this, we can use Equation 6. 13 to calculate the orbital speed: This is quite slow. With a good jump, you could easily launch yourself into an orbit around Deimos! © 2015 Pearson Education, Inc.

Newton’s Law of Gravity and UCM © 2015 Pearson Education, Inc.

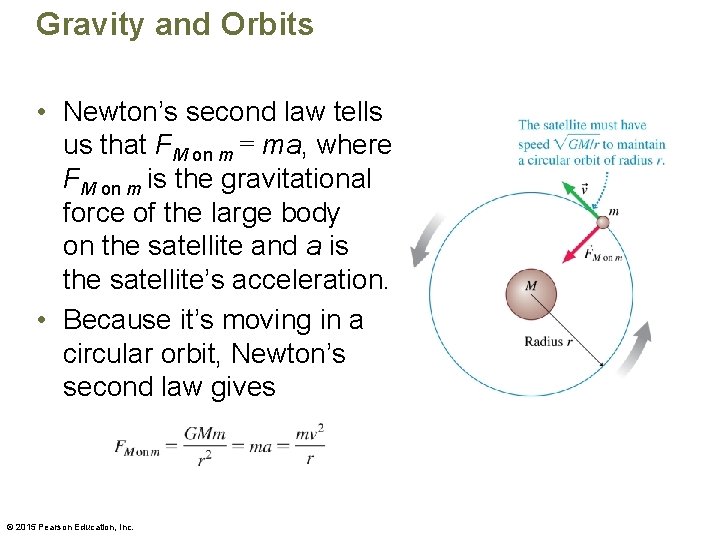
Gravity and Orbits • Newton’s second law tells us that FM on m = ma, where FM on m is the gravitational force of the large body on the satellite and a is the satellite’s acceleration. • Because it’s moving in a circular orbit, Newton’s second law gives © 2015 Pearson Education, Inc.

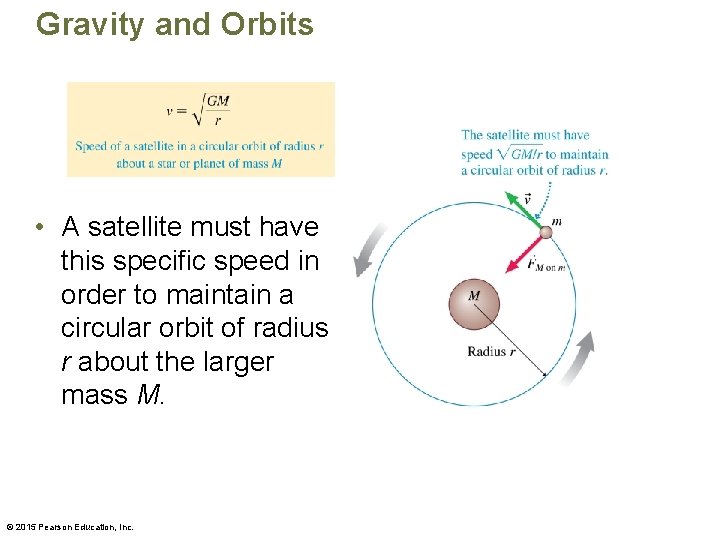
Gravity and Orbits • A satellite must have this specific speed in order to maintain a circular orbit of radius r about the larger mass M. © 2015 Pearson Education, Inc.

Gravity and Orbits • Here is “Keplers 3 rd Law” now proven!!!! © 2015 Pearson Education, Inc.

Question 7 • Two satellites have circular orbits with the same radius. Which has a higher speed? – The one with more mass. – The one with less mass. – They have the same speed. © 2015 Pearson Education, Inc.

Question 7 • Two satellites have circular orbits with the same radius. Which has a higher speed? – The one with more mass. – The one with less mass. – They have the same speed. © 2015 Pearson Education, Inc.

Question 8 • Two identical satellites have different circular orbits. Which has a higher speed? – The one in the larger orbit – The one in the smaller orbit – They have the same speed. © 2015 Pearson Education, Inc.

Question 8 • Two identical satellites have different circular orbits. Which has a higher speed? – The one in the larger orbit – The one in the smaller orbit – They have the same speed. © 2015 Pearson Education, Inc.

Question 9 • A satellite orbits the earth. A Space Shuttle crew is sent to boost the satellite into a higher orbit. Which of these quantities increases? – – – Speed Angular speed Period Centripetal acceleration Gravitational force of the earth © 2015 Pearson Education, Inc.

Question 9 • A satellite orbits the earth. A Space Shuttle crew is sent to boost the satellite into a higher orbit. Which of these quantities increases? – – – Speed Angular speed Period Centripetal acceleration Gravitational force of the earth © 2015 Pearson Education, Inc.

Gravity on a Grand Scale • No matter how far apart two objects may be, there is a gravitational attraction between them. • Galaxies are held together by gravity. • All of the stars in a galaxy are different distances from the galaxy’s center, and so orbit with different periods. © 2015 Pearson Education, Inc.

Satellites and astronauts: Putting it all together • Geostationary satellites stay at the same location in the sky. This is why a satellite dish always points in the same direction. • These satellites must be placed at a specific altitude that allows the satellite to travel once around Earth in exactly 24 hours while remaining above the equator. • An array of such satellites can provide communications to all parts of Earth. © 2014 Pearson Education, Inc.

Example 4. 8: Geostationary satellite • You are in charge of launching a geostationary satellite into orbit. • At which altitude above the equator must the satellite orbit be to provide continuous communication to a stationary dish antenna on Earth? • The mass of Earth is 5. 98 x 1024 kg. 24 hrs to orbit or and a 24 hr period is 86400 sec. © 2014 Pearson Education, Inc.

Example 4. 8: Geostationary satellite © 2014 Pearson Education, Inc.

Example 4. 8 Locating a geostationary satellite (cont. ) This is a high orbit, and the radius is about 7 times the radius of the earth. (26, 221 miles) ASSESS Radius of the International Space Station’s orbit is only about 5% larger than that of the earth. (About 50 km altitude or 5. 0 x 105 m) What is the speed of the Space Station. Will it be more or less than the speed of a satellite at geostationary orbit. © 2015 Pearson Education, Inc.