Chapter 4 Kinematics in Two Dimensions Chapter Goal

Ch. 4 - Student Learning Objectives • To identify the acceleration vector for curvilinear

Acceleration in two dimensions Is the particle speeding up, slowing down, or traveling at

Acceleration in two dimensions Since there is a component of the acceleration vector both

During which time interval is the particle described by these position graphs at rest?

Acceleration is constant along one axis and zero along another Given the initial velocity

Acceleration is constant along one axis and zero along another • This looks like

Acceleration is constant along one axis and zero along another A toy rocket ship

A rocket-powered hockey puck moves on a frictionless horizontal table. It starts at the

Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Projectile motion on another planet A student on planet Exidor throws a ball that

Projectile motion on another planet |g| = 2 m/s 2 θ = tan-1 (v

Uniform Circular Motion Period (T) – the time it takes to go around the

Uniform Circular Motion • For a particle traveling in circular motion, we can describe

Uniform Circular Motion Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

A particle moves cw around a circle at constant speed for 2. 0 s.

Circular Motion – Velocity Vector Components Consider the velocity vector The components are vr

Uniform Circular Motion vt = ds/dt and s = rθ vt = r dθ/dt

Acceleration for uniform circular motion Consider the acceleration vector, graphical vector subtraction shows that:

Rank in order, from largest to smallest, the centripetal accelerations (ar)a to (ar)e of

Nonuniform Circular Motion If the object changes speed: at = dv/dt ar = v

Nonuniform Circular Motion For non-uniform circular motion: • the acceleration vector no longer points

Angular Acceleration at = dv/dt where v = vt vt = r ω at

Relationship between angular and tangential quantities • Point 1 and 2 on the rotating

Angular Acceleration • the graphical relationships for angular velocity and acceleration are the same

Angular Acceleration if α is constant, θ and ω can be found with the

The fan blade is slowing down. What are the signs of ω and α?

Numerical Problem (#36) A 3. 0 cm diameter crankshaft that is rotating at 2500

Convert all non SI units Decide whether time is important Copyright © 2008 Pearson

Note negative sign on the value for at is not solely because it is

Slides: 37

Download presentation

Ch. 4 - Student Learning Objectives • To identify the acceleration vector for curvilinear motion. • To compute two-dimensional trajectories. • To read and interpret graphs of projectile motion. • To solve problems of projectile motion using kinematics equations. • To understand the kinematics of uniform and nonuniform circular motion. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

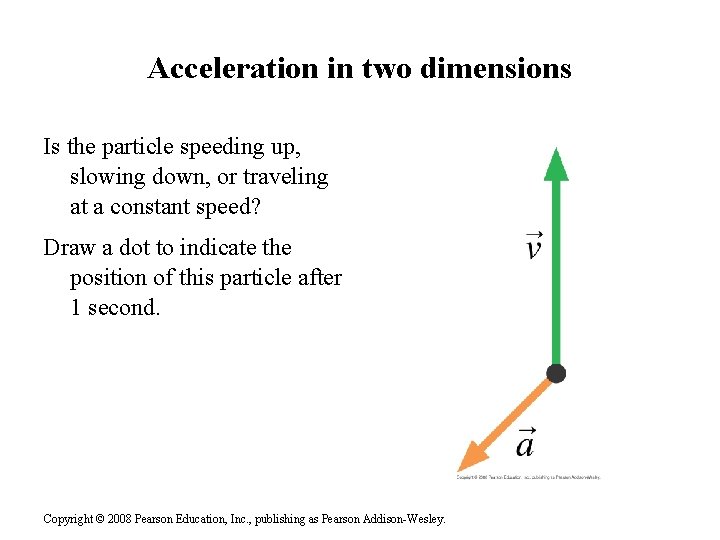
Acceleration in two dimensions Is the particle speeding up, slowing down, or traveling at a constant speed? Draw a dot to indicate the position of this particle after 1 second. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

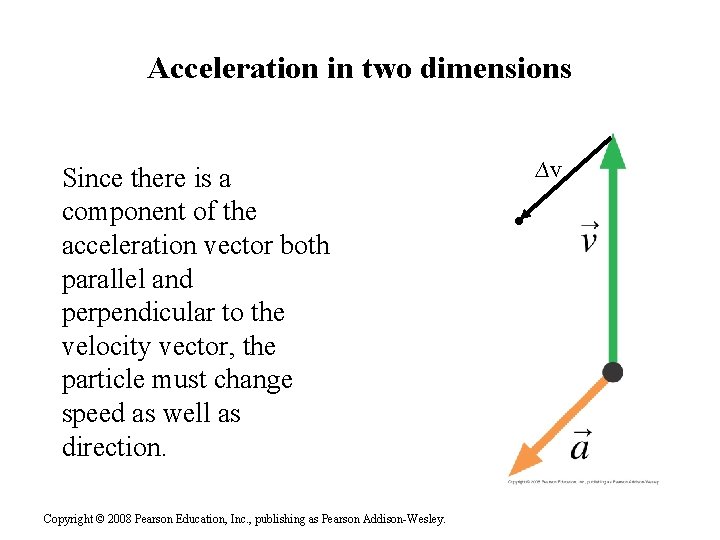
Acceleration in two dimensions Since there is a component of the acceleration vector both parallel and perpendicular to the velocity vector, the particle must change speed as well as direction. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley. ∆v •

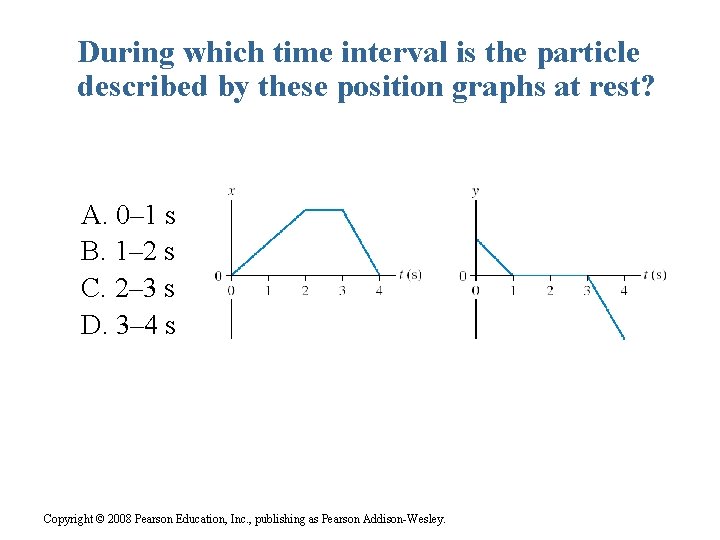
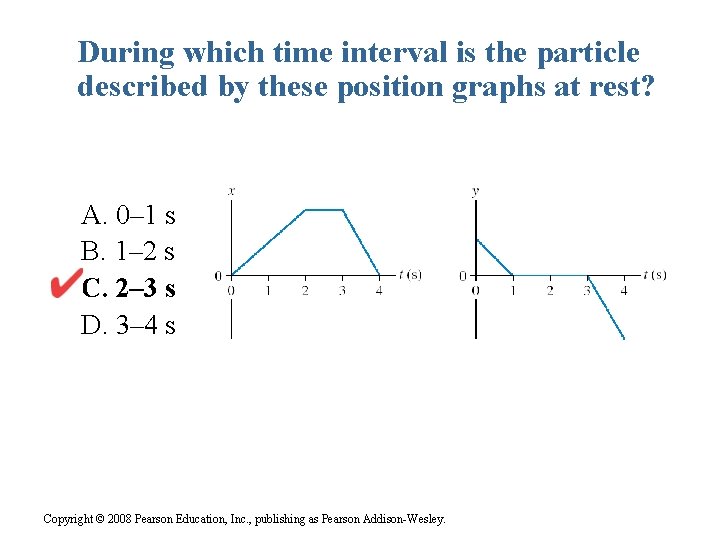
During which time interval is the particle described by these position graphs at rest? A. 0– 1 s B. 1– 2 s C. 2– 3 s D. 3– 4 s Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Acceleration is constant along one axis and zero along another Given the initial velocity vector and acceleration vector shown, construct a motion diagram for a by generating a series of velocity vectors. Assume a time interval of 1 second. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Acceleration is constant along one axis and zero along another • This looks like a parabolic trajectory. • Is this mathematically true? Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Acceleration is constant along one axis and zero along another • This looks like a parabolic trajectory • Is this mathematically true? Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

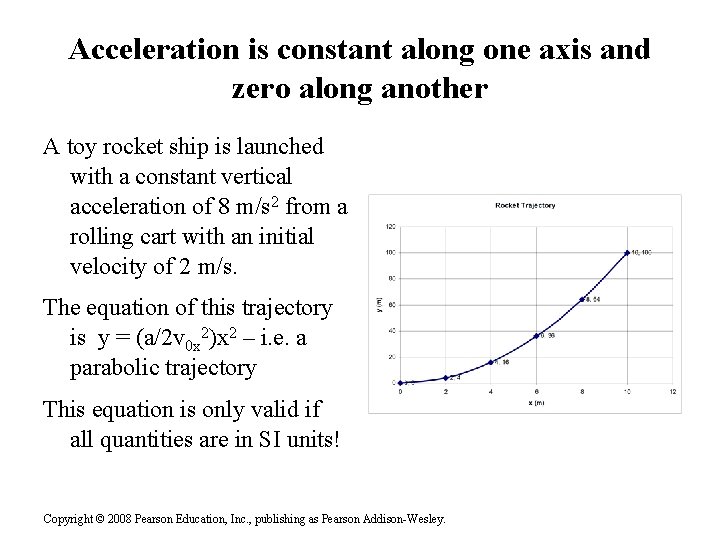
Acceleration is constant along one axis and zero along another A toy rocket ship is launched with a constant vertical acceleration of 8 m/s 2 from a rolling cart with an initial velocity of 2 m/s. Draw a graph of this particle’s trajectory for t = 0, 1, 2, 3, 4 and 5 s. Label the x, y coordinates of each point. Is this a parabolic trajectory? How do you know? Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Acceleration is constant along one axis and zero along another A toy rocket ship is launched with a constant vertical acceleration of 8 m/s 2 from a rolling cart with an initial velocity of 2 m/s. The equation of this trajectory is y = (a/2 v 0 x 2)x 2 – i. e. a parabolic trajectory This equation is only valid if all quantities are in SI units! Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

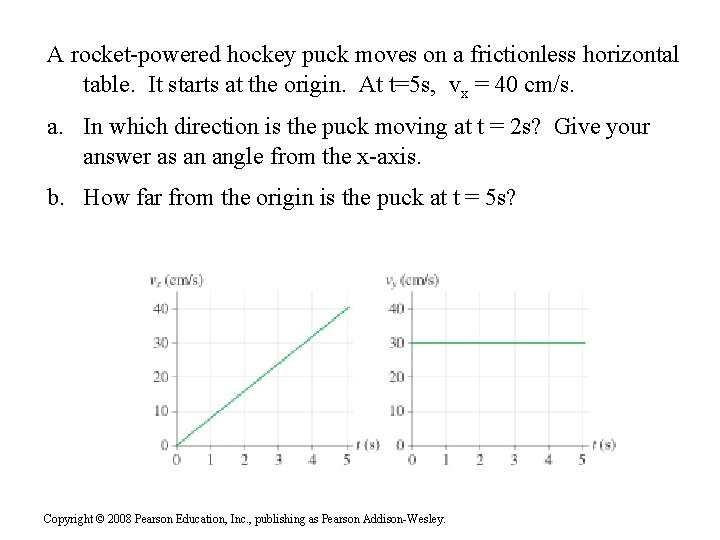
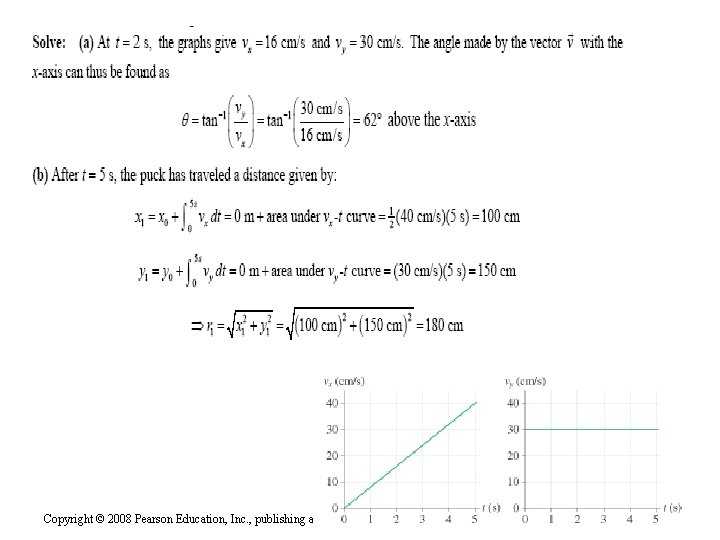
A rocket-powered hockey puck moves on a frictionless horizontal table. It starts at the origin. At t=5 s, vx = 40 cm/s. a. In which direction is the puck moving at t = 2 s? Give your answer as an angle from the x-axis. b. How far from the origin is the puck at t = 5 s? Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

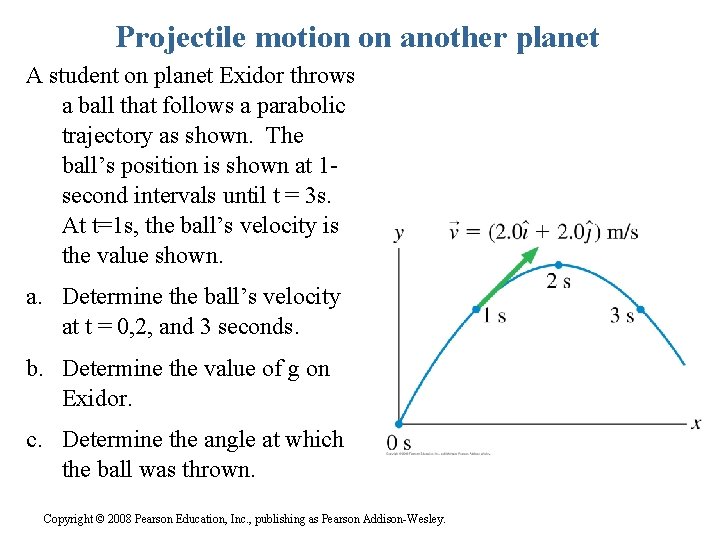
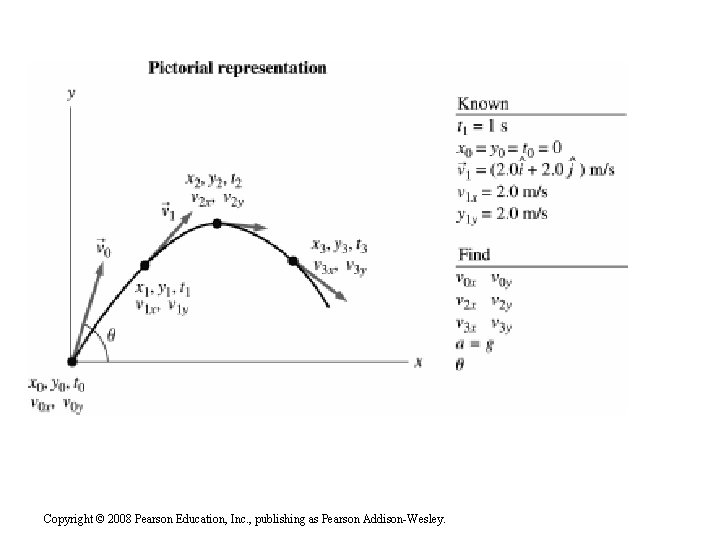
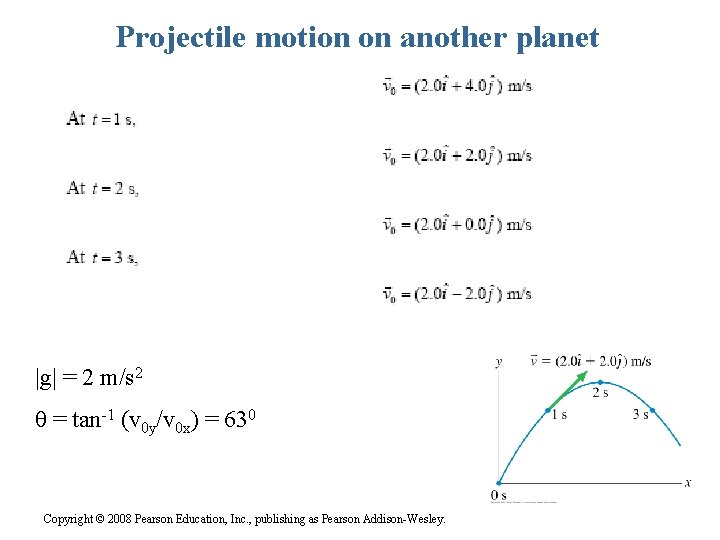
Projectile motion on another planet A student on planet Exidor throws a ball that follows a parabolic trajectory as shown. The ball’s position is shown at 1 second intervals until t = 3 s. At t=1 s, the ball’s velocity is the value shown. a. Determine the ball’s velocity at t = 0, 2, and 3 seconds. b. Determine the value of g on Exidor. c. Determine the angle at which the ball was thrown. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

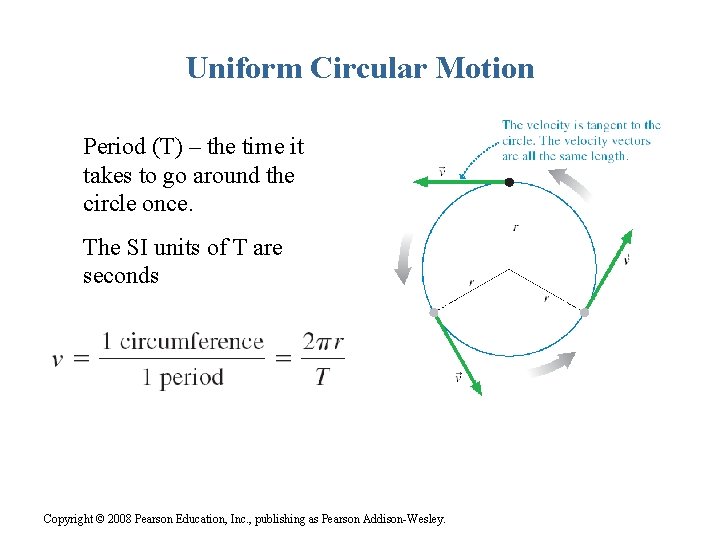
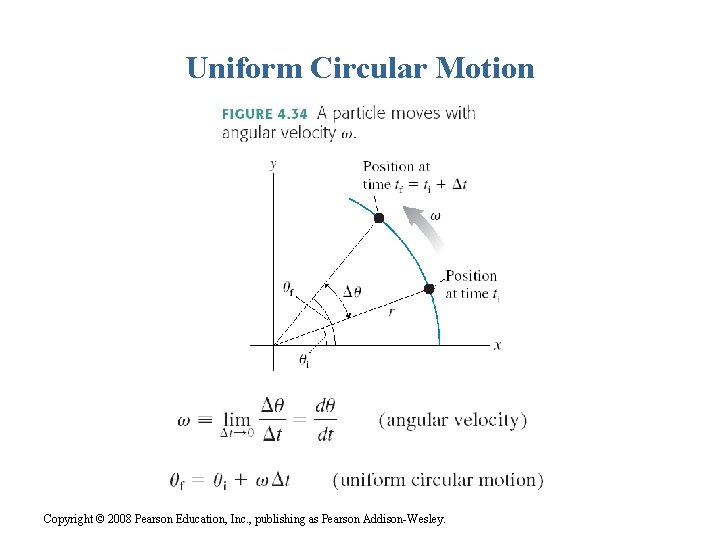
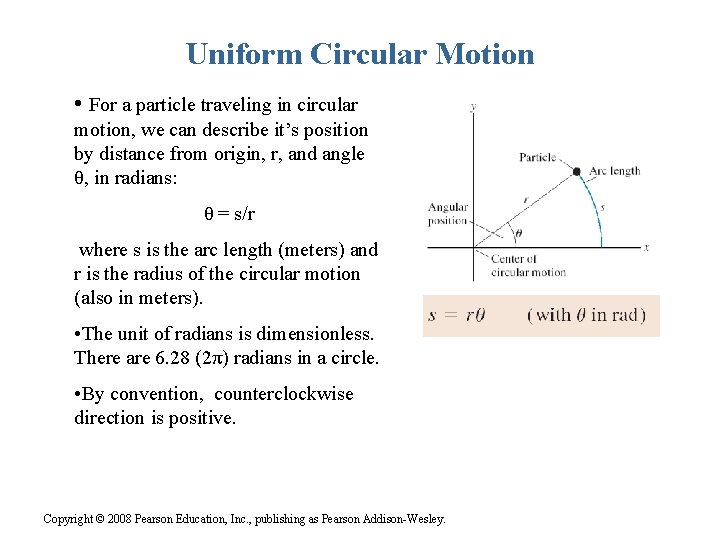
Uniform Circular Motion • For a particle traveling in circular motion, we can describe it’s position by distance from origin, r, and angle θ, in radians: θ = s/r where s is the arc length (meters) and r is the radius of the circular motion (also in meters). • The unit of radians is dimensionless. There are 6. 28 (2π) radians in a circle. • By convention, counterclockwise direction is positive. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

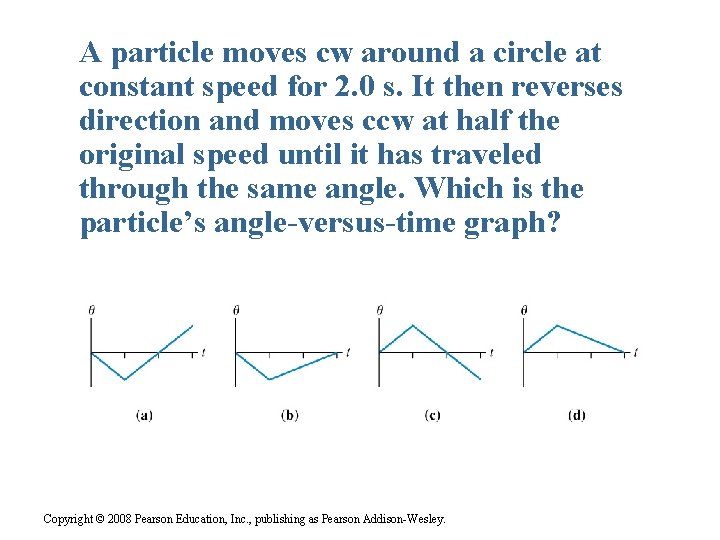
A particle moves cw around a circle at constant speed for 2. 0 s. It then reverses direction and moves ccw at half the original speed until it has traveled through the same angle. Which is the particle’s angle-versus-time graph? Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Circular Motion – Velocity Vector Components Consider the velocity vector The components are vr = 0, vt = where r denotes radial component and t denotes tangential component. For tangential components, ccw = positive, cw = negative. For radial components, positive is into the center of the circle. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Acceleration for uniform circular motion Consider the acceleration vector, graphical vector subtraction shows that: at = 0, ar = It can be shown that: ar = v 2/r or ar = ω2 r For uniform circular motion, the magnitude of a is constant, but direction is not, so kinematic equations are not valid. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Rank in order, from largest to smallest, the centripetal accelerations (ar)a to (ar)e of particles a to e. 1. (ar)b > (ar)e > (ar)a = (ar)c > (ar)d Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Nonuniform Circular Motion If the object changes speed: at = dv/dt ar = v 2/r where v is the instantaneous speed. if at is constant, arc length s and velocity vt can be found with kinematic equations. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Nonuniform Circular Motion For non-uniform circular motion: • the acceleration vector no longer points towards the center of the circle. • at can be positive (ccw) or negative (cw) but ar is always positive. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

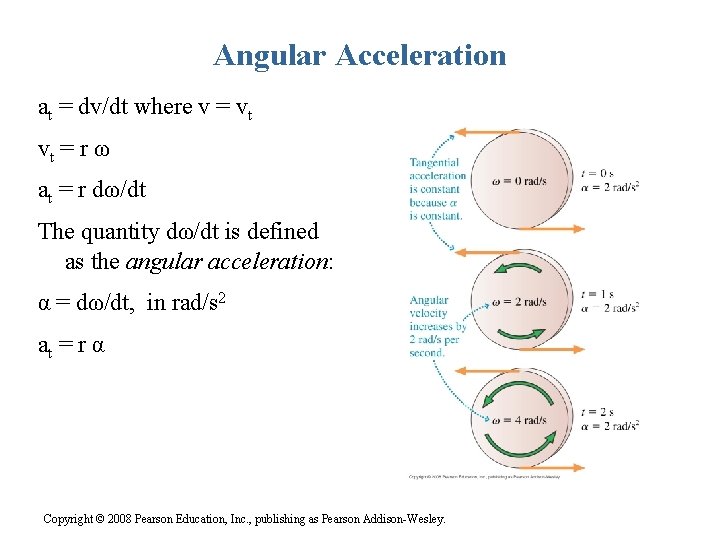
Angular Acceleration at = dv/dt where v = vt vt = r ω at = r dω/dt The quantity dω/dt is defined as the angular acceleration: α = dω/dt, in rad/s 2 at = r α Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

Relationship between angular and tangential quantities • Point 1 and 2 on the rotating wheel have different radii. θ 1 = θ 2 but s 1 ≠ s 2 ω1=ω2 but v 1 ≠ v 2 α 1= α 2 but at 1 ≠ at 2 Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

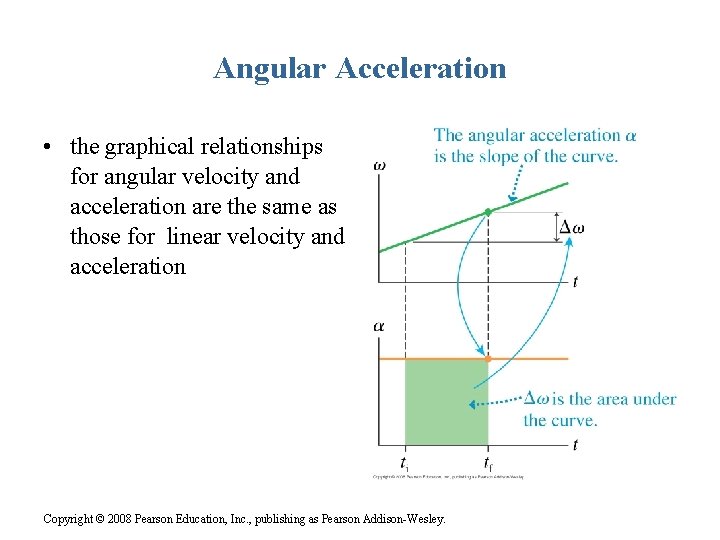
Angular Acceleration • the graphical relationships for angular velocity and acceleration are the same as those for linear velocity and acceleration Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

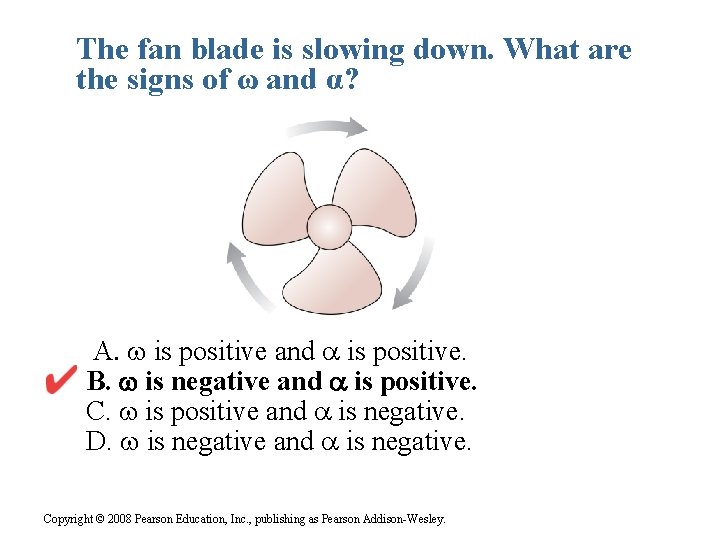
The fan blade is slowing down. What are the signs of ω and α? is positive and is positive. B. is negative and is positive. C. is positive and is negative. D. is negative and is negative. Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.

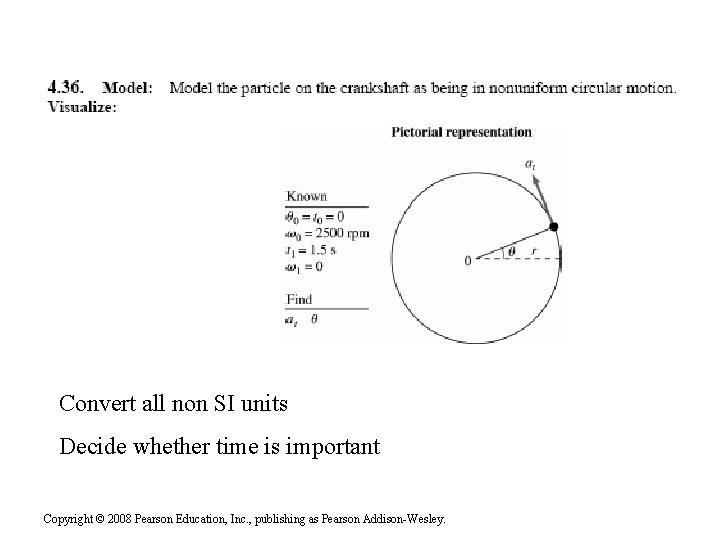
Numerical Problem (#36) A 3. 0 cm diameter crankshaft that is rotating at 2500 rpm comes to a halt in 1. 5 s. a. What is the tangential acceleration of a point on the surface? b. How many revolutions does the crankshaft make as it stops? Copyright © 2008 Pearson Education, Inc. , publishing as Pearson Addison-Wesley.