Chapter 4 Kinematics in Two Dimensions 1 TwoDimension

Chapter 4: Kinematics in Two Dimensions 1. Two-Dimension Kinematics 2. Projectile Motion 3. Relative Motion 4. Uniform Circular Motion 5. Velocity and Acceleration in Uniform Circular Motion 6. Nonuniform Circular Motion

Stop to think 4. 1 Stop to think 4. 2 Stop to think 4. 3 Stop to think 4. 4 Stop to think 4. 5 Stop to think 4. 3 4. 6 n Example 4. 4 n Example 4. 5 n Example 4. 6 n Example 4. 9 n Example 4. 13 n Example 4. 15 P 93 P 97 P 102 P 107 P 110 P 113 P 97 P 98 P 100 P 101 P 106 P 110 P 114

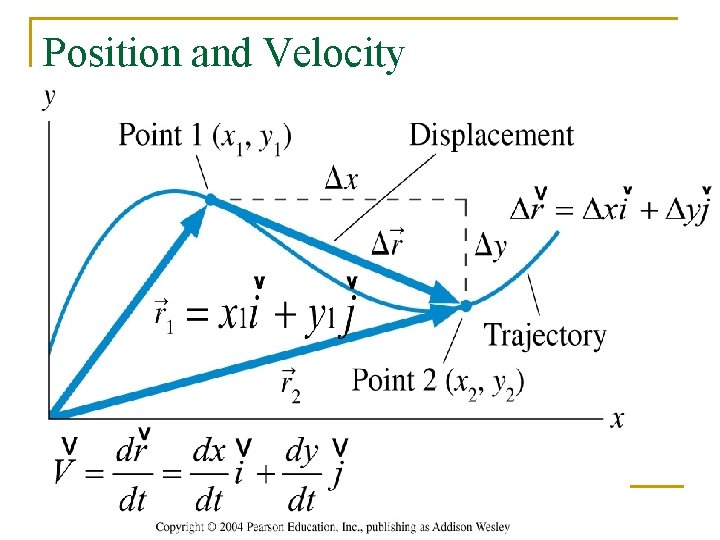
Position and Velocity

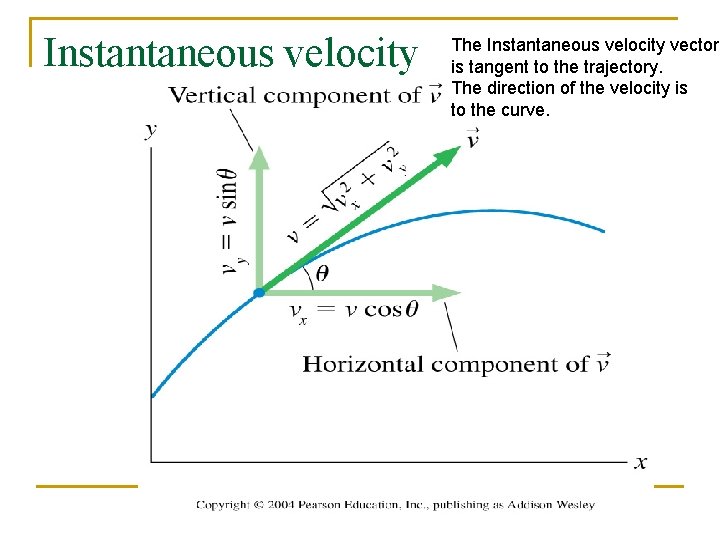
Instantaneous velocity The Instantaneous velocity vector is tangent to the trajectory. The direction of the velocity is to the curve.

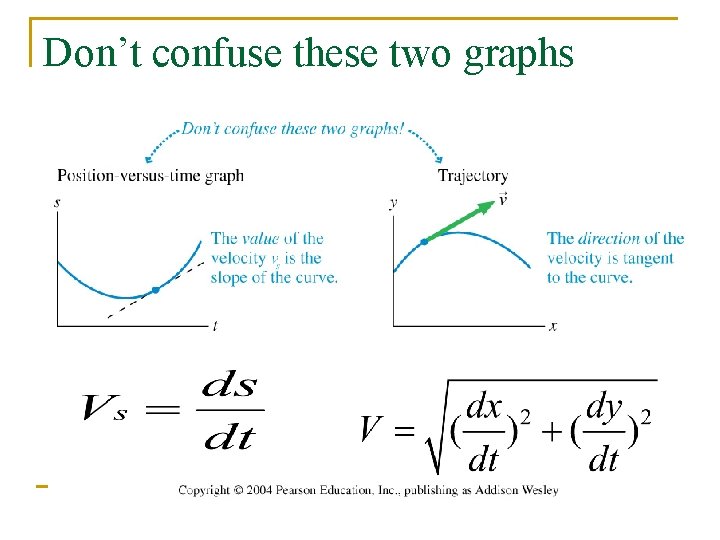
Don’t confuse these two graphs

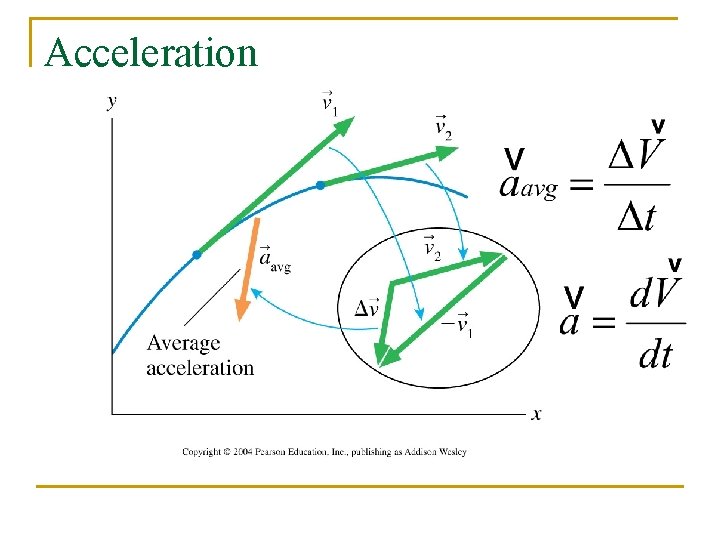
Acceleration

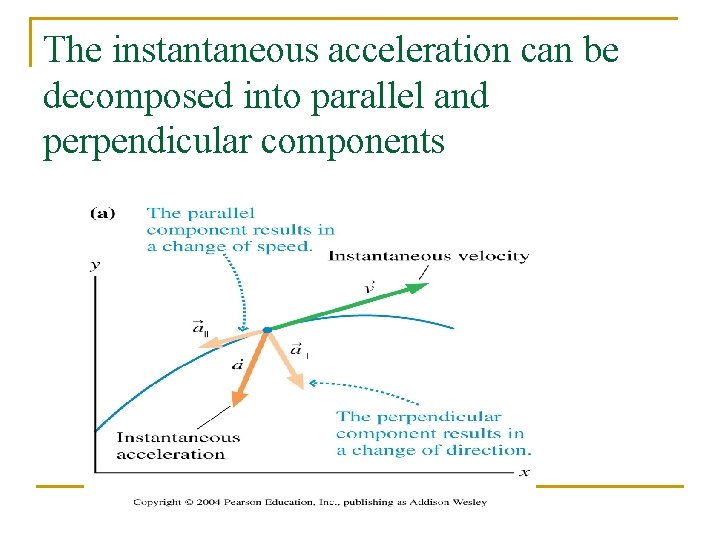
The instantaneous acceleration can be decomposed into parallel and perpendicular components

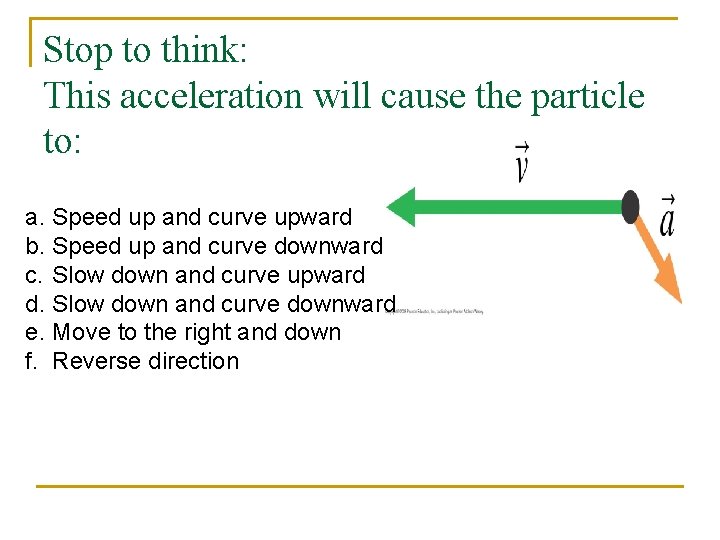
Stop to think: This acceleration will cause the particle to: a. Speed up and curve upward b. Speed up and curve downward c. Slow down and curve upward d. Slow down and curve downward e. Move to the right and down f. Reverse direction

Projectile Motion object moves in two dimensions under the gravitational force. B A 1. What is the accelerations at position A and B? 2. What is the velocities at position A and B?

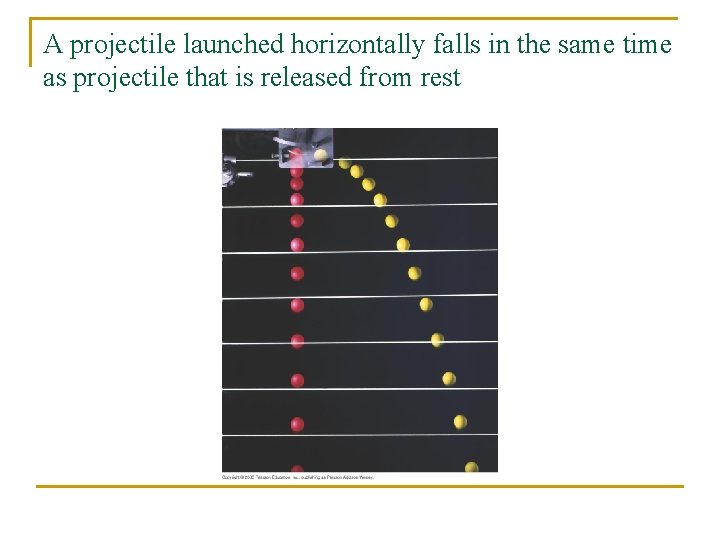
A projectile launched horizontally falls in the same time as projectile that is released from rest

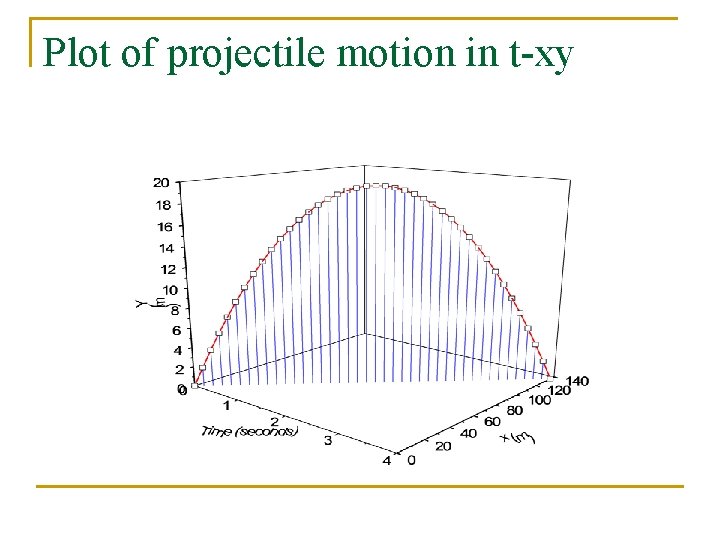
Plot of projectile motion in t-xy

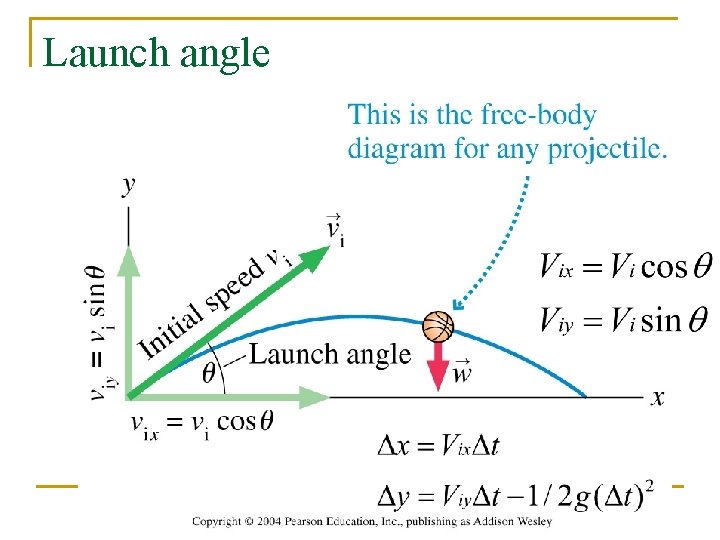
Launch angle

Ex. A ball thrown horizontally at velocity Vi , travels a horizontal distance of R m before hitting the ground. From what height was the ball thrown? (1) Since ball is thrown horizontally, Vi =Vx There is no acceleration at x direction. ie. R = Vxt, t = R/Vx (2) Viy=0, h = -1/2 gt 2

Problem 50 Solve a quadratic equation to get t

The maximum height and distance of fly ball n For projectile motion, always remember:

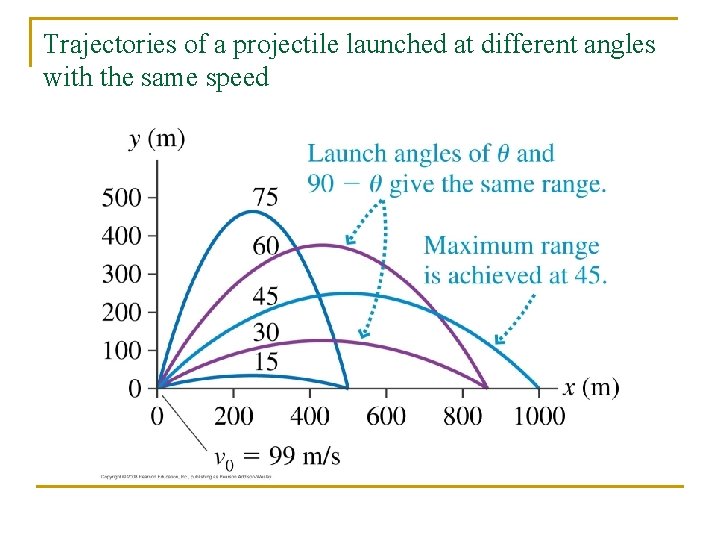
Trajectories of a projectile launched at different angles with the same speed

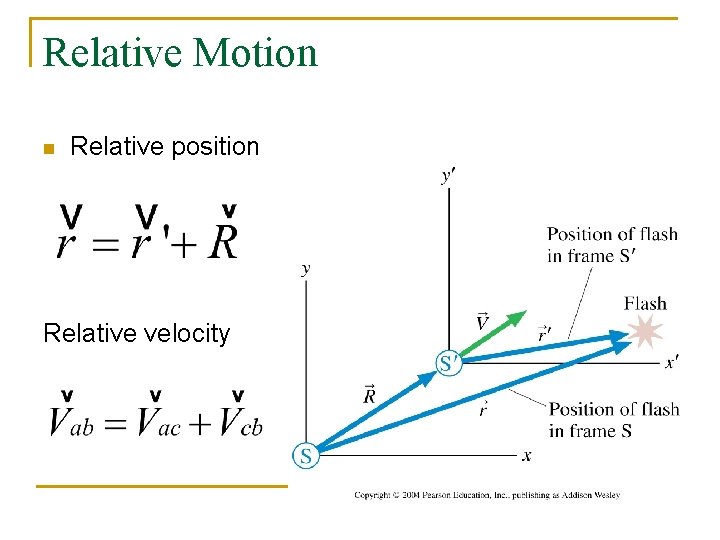
Relative Motion n Relative position Relative velocity

Uniform Circular Motion n n Period Angular Position

Angular Velocity n Average angular velocity =∆θ/∆t n Instantaneous angular velocity n The angular velocity is constant during uniform circular motion

An old-fashioned single-play vinyl record rotates 30. 0 rpm. What are (a) the angular velocity in rad/s and (b) the period of the motion? n rpm: revolution per minute. 1 rpm = 2π/60 (rad)/s

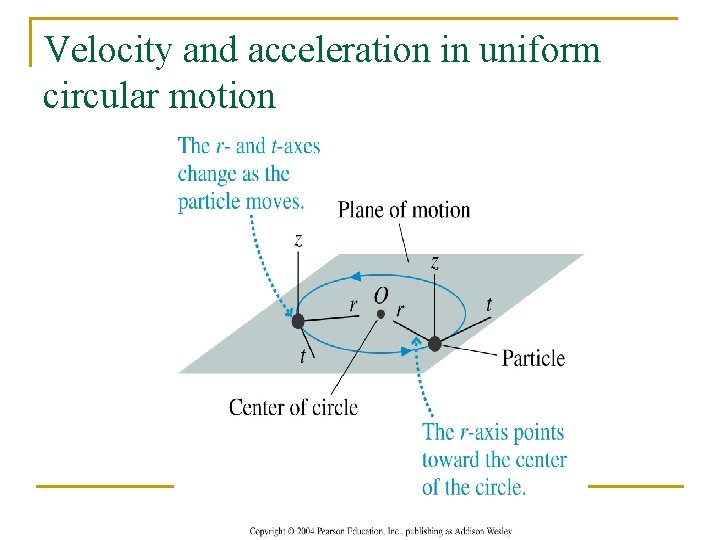
Velocity and acceleration in uniform circular motion

Velocity in uniform circular motion The magnitude of velocity is a constant Vt =r dθ/dt =ωr Has only a tangential Component

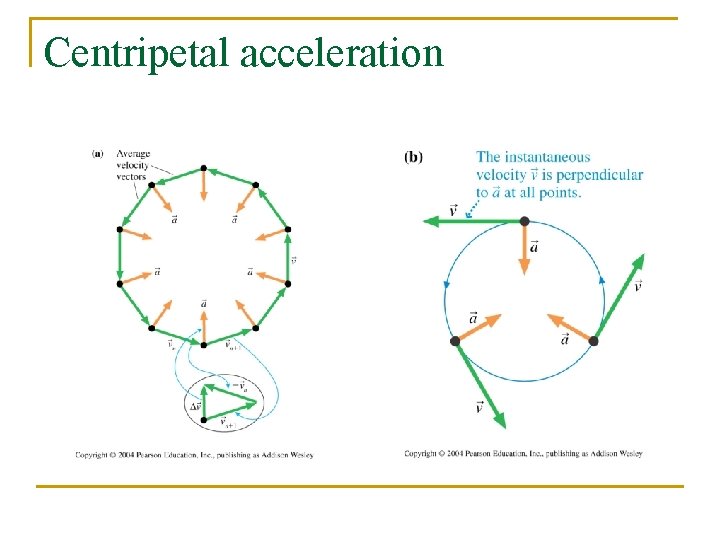
Centripetal acceleration

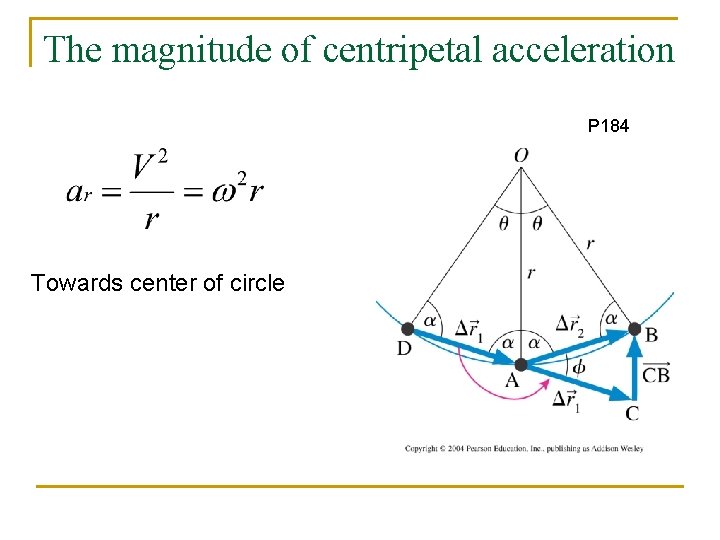
The magnitude of centripetal acceleration P 184 Towards center of circle

Velocity and acceleration in Uniform Circular Motion The velocity has only a tangential component Vt

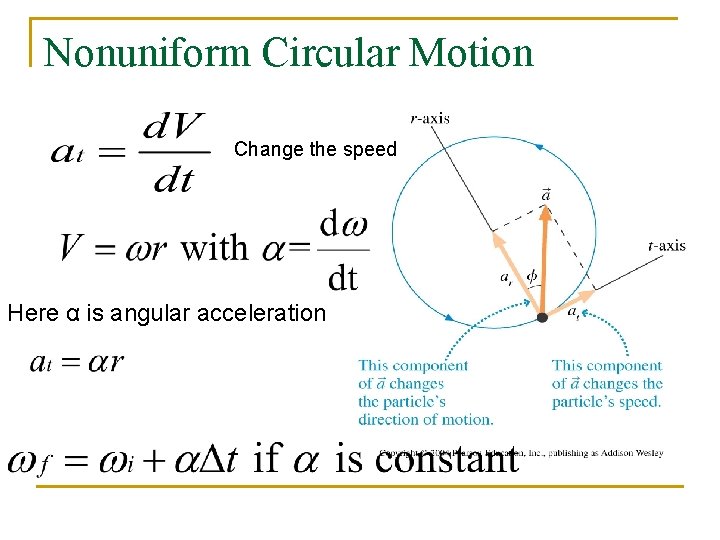
Nonuniform Circular Motion Change the speed Here α is angular acceleration

Rotational kinematics n For constant angular acceleration