Chapter 4 Introduction to Eventbased Modeling Simulation Little

Chapter 4 Introduction to Event-based Modeling & Simulation “Little people discuss other people. Average people discuss events. Big people discuss ideas. ” – quoted by R. E. Kalman Last revision July 14, 2013 For more information on this book and materials, visit the official website, http: //www. vms-technology. com/book/

1. Introduction (1/1) If something that happened results in some meaningful changes it is called an event. If we can identify the logical and temporal relationships among those events, we understand our present situation better and may even be able to predict the future. 1. Introduction 2. Modeling and Simulation of Single Server System 3. Execution Rules and Specifications of Event Graph 4. Event Graph Modeling Templates 5. Event Graph Modeling Examples 6. Execution of Event Graph Models with SIGMA® 7. Developing Your Own Event Graph Simulator Modeling and Simulation of Discrete-Event Systems No. 2 Chapter 4 – Introduction to Event-based M&S

2. Modeling & Simulation of Single Server System (0/2) Table of Contents 2 -1. Event-based Modeling of Single Server System 2 -2. Simulation of Single Server System Modeling and Simulation of Discrete-Event Systems No. 3 Chapter 4 – Introduction to Event-based M&S

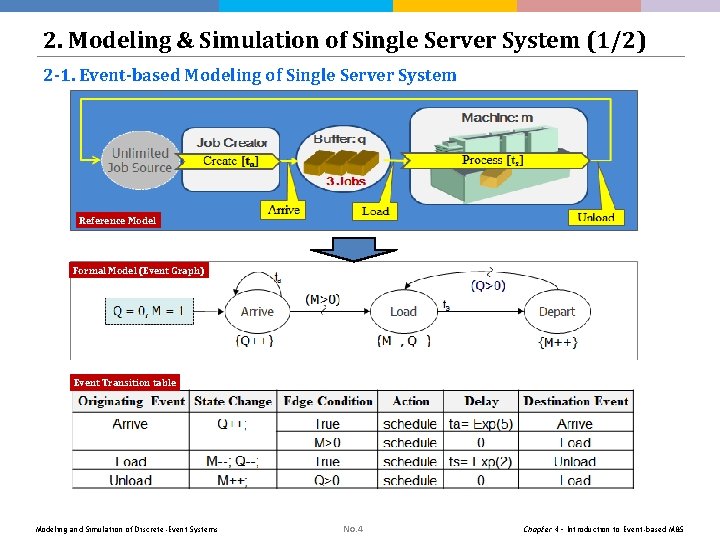
2. Modeling & Simulation of Single Server System (1/2) 2 -1. Event-based Modeling of Single Server System Reference Model Formal Model (Event Graph) Event Transition table Modeling and Simulation of Discrete-Event Systems No. 4 Chapter 4 – Introduction to Event-based M&S

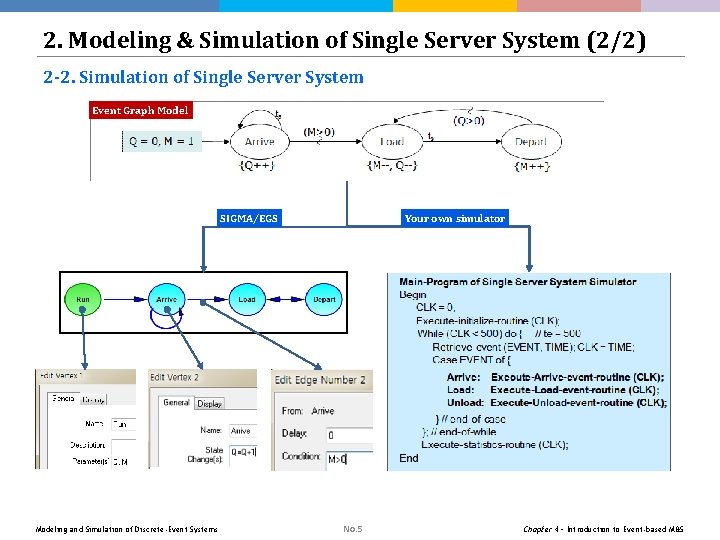
2. Modeling & Simulation of Single Server System (2/2) 2 -2. Simulation of Single Server System Event Graph Model SIGMA/EGS Modeling and Simulation of Discrete-Event Systems Your own simulator No. 5 Chapter 4 – Introduction to Event-based M&S

3. Execution Rules and Specifications of Event Graph (0/3) Table of Contents 3 -1. Event Graph Execution Rules 3 -2. Tabular Specification of Event Graph Model 3 -3. Algebraic Specification of Event Graph Modeling and Simulation of Discrete-Event Systems No. 6 Chapter 4 – Introduction to Event-based M&S

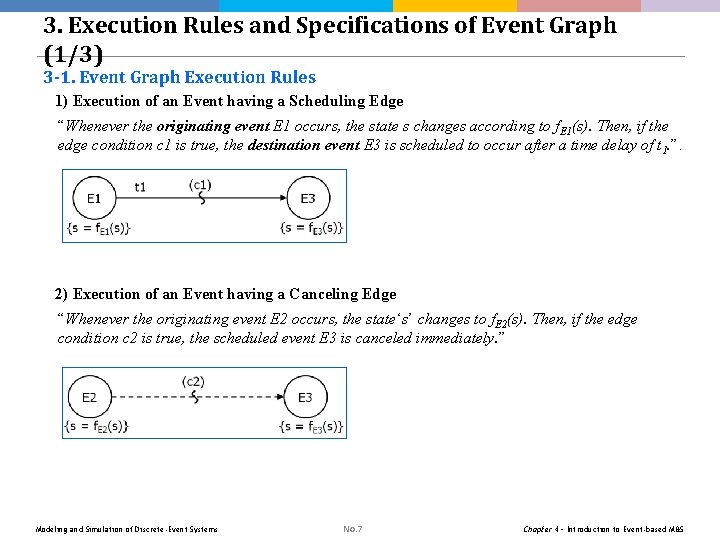
3. Execution Rules and Specifications of Event Graph (1/3) 3 -1. Event Graph Execution Rules 1) Execution of an Event having a Scheduling Edge “Whenever the originating event E 1 occurs, the state s changes according to f. E 1(s). Then, if the edge condition c 1 is true, the destination event E 3 is scheduled to occur after a time delay of t 1. ”. 2) Execution of an Event having a Canceling Edge “Whenever the originating event E 2 occurs, the state‘s’ changes to f. E 2(s). Then, if the edge condition c 2 is true, the scheduled event E 3 is canceled immediately. ” Modeling and Simulation of Discrete-Event Systems No. 7 Chapter 4 – Introduction to Event-based M&S

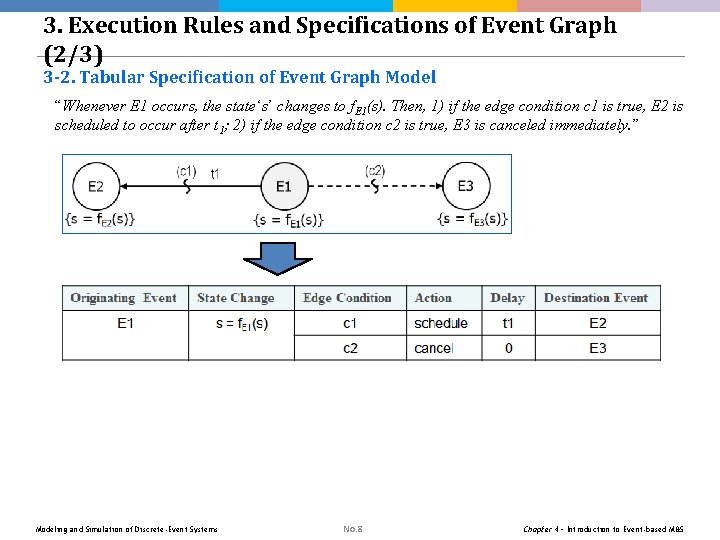
3. Execution Rules and Specifications of Event Graph (2/3) 3 -2. Tabular Specification of Event Graph Model “Whenever E 1 occurs, the state‘s’ changes to f. E 1(s). Then, 1) if the edge condition c 1 is true, E 2 is scheduled to occur after t 1; 2) if the edge condition c 2 is true, E 3 is canceled immediately. ” Modeling and Simulation of Discrete-Event Systems No. 8 Chapter 4 – Introduction to Event-based M&S

3. Execution Rules and Specifications of Event Graph (3/3) 3 -3. Algebraic Specification of Event Graph Model An event graph is a directed graph consisting of a set of event vertices V, a set of directed edges E, and a set of state variables S. The edge set E represents the temporal and logical relationships between a pair of vertices. Associated with each vertex v ∈ V is state transition function fv; associated with each edge e ∈ E are an edge condition ce ∈ C, time delay de ∈ D, and action type ae ∈ A (schedule or cancel). Thus, an event graph model M can be defined as a 7 -tuple structure. Modeling and Simulation of Discrete-Event Systems No. 9 Chapter 4 – Introduction to Event-based M&S

1. 2. 3. 4. 5. 6. 7. 8. M = <V, E, S, F, C, D, A>, where V = {v}: set of event vertices E = {eod= (vo, vd)}: set of edges // vo: originating event; vd: destination event S = {s}: set of state variables F = {fv: S → S ∀v ∈ V}: set of state transition functions associated with V C = {ce: S→[0, 1] ∀e ∈ E}: set of conditions associated with E D = {de R 0 ∀e ∈ E}: set of time delays associated with E A = {ae ∈ [scheduling, canceling] ∀e ∈ E}: action type set H/W-1(Exercise 4. 1): Specify the algebraic components of the event graph in Figure 4. 5. Modeling and Simulation of Discrete-Event Systems No. 10 Chapter 4 – Introduction to Event-based M&S

4. Event Graph Modeling Templates (1/6) Table of Contents 4 -1. Single Queue Models (1) Multiple Server Models (Flexible multi-server Template) (2) Limited Waiting Space Model (Balking Template) (3) Impatient Customer Model (Reneging with balking) (4) Non-stationary Arrival Rate Model (Fluctuating arrival Template) (5) Batched Service Models (6) Assembly Operation Model (7) Resource Priority Model (8) A Resource Failure Models 4 -2. Tandem Queue Models (1) Limited-buffer Tandem Queue Model (2) Time-constrained Processing Tandem Queue Model) Modeling and Simulation of Discrete-Event Systems No. 11 Chapter 4 – Introduction to Event-based M&S

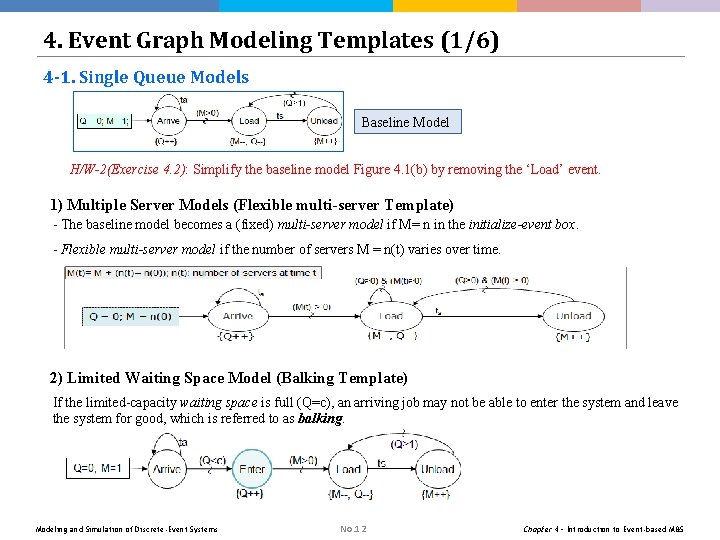
4. Event Graph Modeling Templates (1/6) 4 -1. Single Queue Models Baseline Model H/W-2(Exercise 4. 2): Simplify the baseline model Figure 4. 1(b) by removing the ‘Load’ event. 1) Multiple Server Models (Flexible multi-server Template) - The baseline model becomes a (fixed) multi-server model if M= n in the initialize-event box. - Flexible multi-server model if the number of servers M = n(t) varies over time. 2) Limited Waiting Space Model (Balking Template) If the limited-capacity waiting space is full (Q=c), an arriving job may not be able to enter the system and leave the system for good, which is referred to as balking. Modeling and Simulation of Discrete-Event Systems No. 12 Chapter 4 – Introduction to Event-based M&S

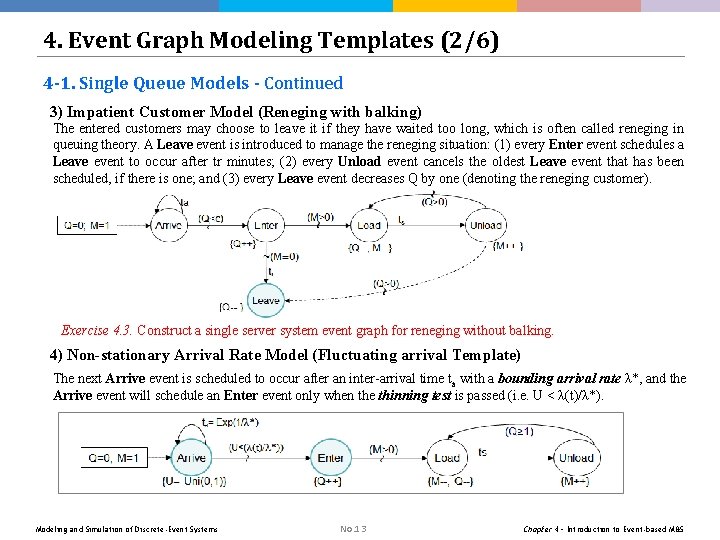
4. Event Graph Modeling Templates (2/6) 4 -1. Single Queue Models - Continued 3) Impatient Customer Model (Reneging with balking) The entered customers may choose to leave it if they have waited too long, which is often called reneging in queuing theory. A Leave event is introduced to manage the reneging situation: (1) every Enter event schedules a Leave event to occur after tr minutes; (2) every Unload event cancels the oldest Leave event that has been scheduled, if there is one; and (3) every Leave event decreases Q by one (denoting the reneging customer). Exercise 4. 3. Construct a single server system event graph for reneging without balking. 4) Non-stationary Arrival Rate Model (Fluctuating arrival Template) The next Arrive event is scheduled to occur after an inter-arrival time ta with a bounding arrival rate λ*, and the Arrive event will schedule an Enter event only when the thinning test is passed (i. e. U < λ(t)/λ*). Modeling and Simulation of Discrete-Event Systems No. 13 Chapter 4 – Introduction to Event-based M&S

4. Event Graph Modeling Templates (3/6) 4 -1. Single Queue Models - Continued 5) Batched Service Models Batched service occurs when a batch of jobs is processed at the same time. In general, there are maximum number (b) and minimum number (a) of jobs that can be processed at a time, which is denoted as ‘a ≤ J ≤ b’ where J is the actual number of jobs in a batched service. If a = b, we have a full-batched service; if a < b, we have a partial-batched service. H/W-3(Exercise 4. 4): Revise the event graph presented in Figure 4. 10 to make it a partial batched service model 6) Assembly Operation Model Parts of type j for j=1, 2 arrive at the system every tj minutes, and a pair of parts, one from each type, are assembled together by a machine. Let Q denote number of part pairs and Pj denote number of parts of type j, then the assembly operation is modeled as follows: Modeling and Simulation of Discrete-Event Systems No. 14 Chapter 4 – Introduction to Event-based M&S

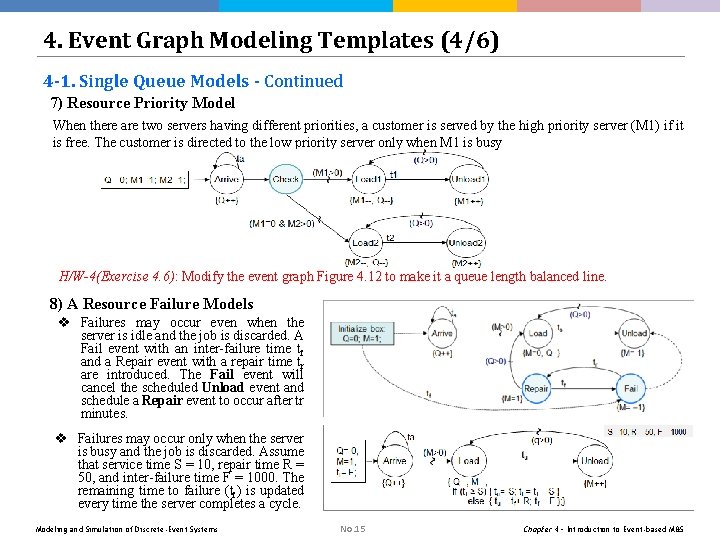
4. Event Graph Modeling Templates (4/6) 4 -1. Single Queue Models - Continued 7) Resource Priority Model When there are two servers having different priorities, a customer is served by the high priority server (M 1) if it is free. The customer is directed to the low priority server only when M 1 is busy H/W-4(Exercise 4. 6): Modify the event graph Figure 4. 12 to make it a queue length balanced line. 8) A Resource Failure Models v Failures may occur even when the server is idle and the job is discarded. A Fail event with an inter-failure time tf and a Repair event with a repair time tr are introduced. The Fail event will cancel the scheduled Unload event and schedule a Repair event to occur after tr minutes. v Failures may occur only when the server is busy and the job is discarded. Assume that service time S = 10, repair time R = 50, and inter-failure time F = 1000. The remaining time to failure (tf) is updated every time the server completes a cycle. Modeling and Simulation of Discrete-Event Systems No. 15 Chapter 4 – Introduction to Event-based M&S

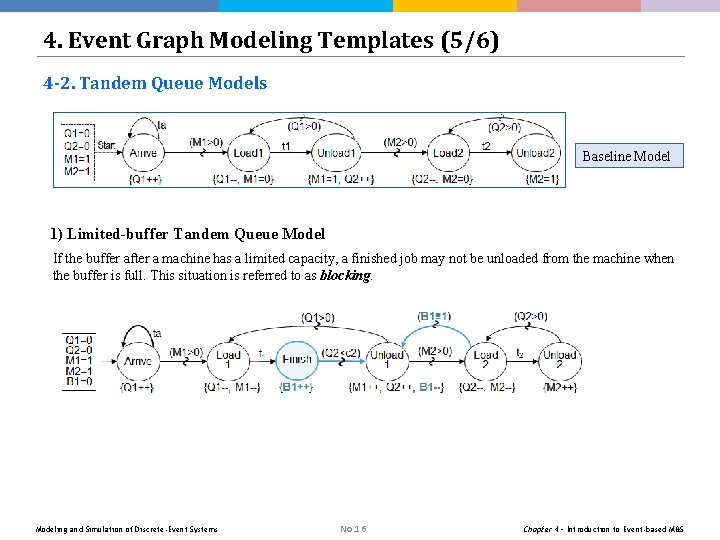
4. Event Graph Modeling Templates (5/6) 4 -2. Tandem Queue Models Baseline Model 1) Limited-buffer Tandem Queue Model If the buffer after a machine has a limited capacity, a finished job may not be unloaded from the machine when the buffer is full. This situation is referred to as blocking. Modeling and Simulation of Discrete-Event Systems No. 16 Chapter 4 – Introduction to Event-based M&S

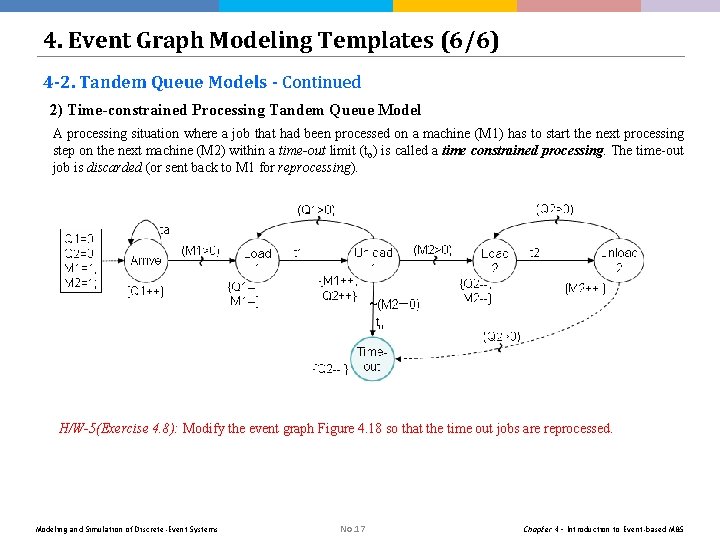
4. Event Graph Modeling Templates (6/6) 4 -2. Tandem Queue Models - Continued 2) Time-constrained Processing Tandem Queue Model A processing situation where a job that had been processed on a machine (M 1) has to start the next processing step on the next machine (M 2) within a time-out limit (to) is called a time constrained processing. The time-out job is discarded (or sent back to M 1 for reprocessing). H/W-5(Exercise 4. 8): Modify the event graph Figure 4. 18 so that the time out jobs are reprocessed. Modeling and Simulation of Discrete-Event Systems No. 17 Chapter 4 – Introduction to Event-based M&S

5. Event Graph Modeling Examples (0/11) Table of Contents 5 -1. Simple Service Shop (Flexible Multi-Server System) Modeling 5 -2. Car Repair Modeling 5 -3. Project Management Modeling 5 -4. Conveyor-driven Serial Line Modeling 5 -5. Inline-type Manufacturing Cell Modeling and Simulation of Discrete-Event Systems No. 18 Chapter 4 – Introduction to Event-based M&S

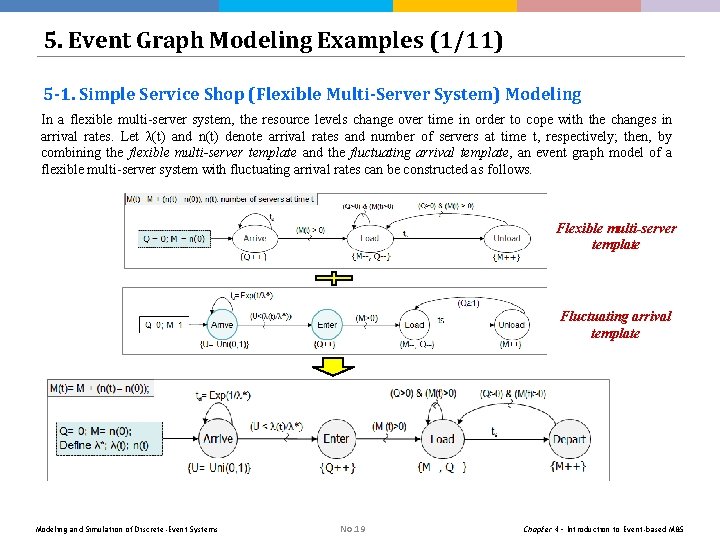
5. Event Graph Modeling Examples (1/11) 5 -1. Simple Service Shop (Flexible Multi-Server System) Modeling In a flexible multi-server system, the resource levels change over time in order to cope with the changes in arrival rates. Let λ(t) and n(t) denote arrival rates and number of servers at time t, respectively; then, by combining the flexible multi-server template and the fluctuating arrival template, an event graph model of a flexible multi-server system with fluctuating arrival rates can be constructed as follows. Flexible multi-server template Fluctuating arrival template Modeling and Simulation of Discrete-Event Systems No. 19 Chapter 4 – Introduction to Event-based M&S

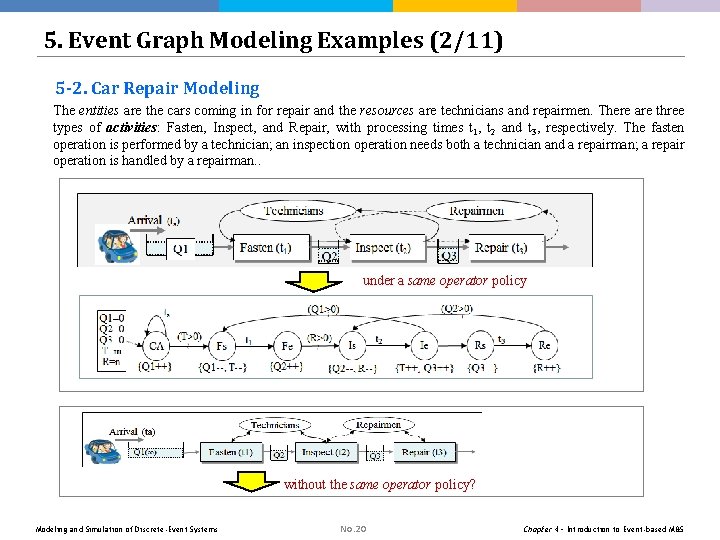
5. Event Graph Modeling Examples (2/11) 5 -2. Car Repair Modeling The entities are the cars coming in for repair and the resources are technicians and repairmen. There are three types of activities: Fasten, Inspect, and Repair, with processing times t 1, t 2 and t 3, respectively. The fasten operation is performed by a technician; an inspection operation needs both a technician and a repairman; a repair operation is handled by a repairman. . under a same operator policy without the same operator policy? Modeling and Simulation of Discrete-Event Systems No. 20 Chapter 4 – Introduction to Event-based M&S

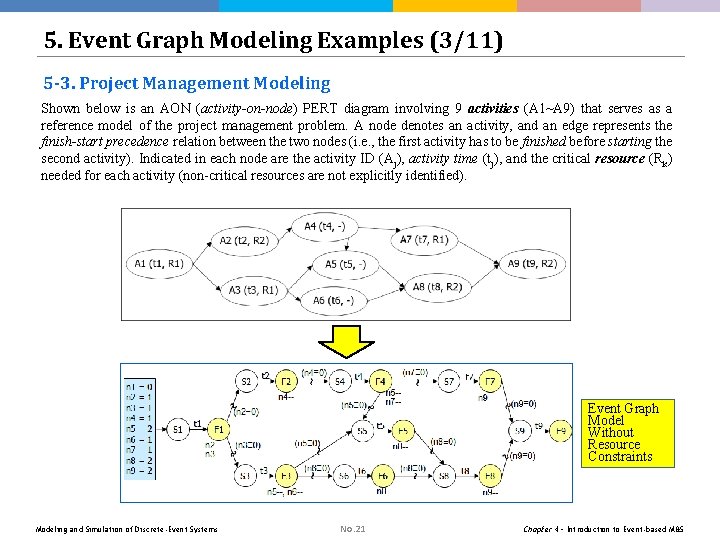
5. Event Graph Modeling Examples (3/11) 5 -3. Project Management Modeling Shown below is an AON (activity-on-node) PERT diagram involving 9 activities (A 1~A 9) that serves as a reference model of the project management problem. A node denotes an activity, and an edge represents the finish-start precedence relation between the two nodes (i. e. , the first activity has to be finished before starting the second activity). Indicated in each node are the activity ID (Aj), activity time (tj), and the critical resource (Rk) needed for each activity (non-critical resources are not explicitly identified). Event Graph Model Without Resource Constraints Modeling and Simulation of Discrete-Event Systems No. 21 Chapter 4 – Introduction to Event-based M&S

5. Event Graph Modeling Examples (4/11) 5 -4. Conveyor-driven Serial Line Modeling Consider a 3 -stage serial production line shown in Fig. 4. 30 consisting of three work stations (WS) connected by conveyors (CV). Base-parts (jobs) stored in the input buffer (Buffer-I) are moved along the line, and sub-parts are assembled to the base-part at each work station. The assembled base-parts (i. e. , products) are stored in the output buffer (Buffer-O). Entities in the system are the base-parts, and resources are the WSs, CVs and Buffers. Activities are the production operations at the WSs and the transport operations by the conveyors. pj = processing time at WS j; tj = transport time of the conveyor-j; cj = capacity of CVj (c 1 = cn+1 = ∞). Modeling and Simulation of Discrete-Event Systems Mj = workstation-j status (1: free, 0: busy); Bj = blocking of workstation-j (1: blocked), Qj = total number of jobs at CV-j, and Rj = number of jobs ready at CV-j (that have been transported). No. 22 Chapter 4 – Introduction to Event-based M&S

5. Event Graph Modeling Examples (5/11) 5 -5. Inline-type Manufacturing Cell Modeling (0) Source System Description In the photolithography cell found in a modern TFT-LCD (thin film transistor-liquid crystal display) panel Fab, the jobs are glasses that go through photoresist (PR) coating, exposure, and development processes in the cell. The glasses are handled in batches with each batch stored in a cassette. The arriving cassettes that are stored in the inline stocker are moved into the I/O port, which is called the cassette loading (CL) operation. The glasses are loaded inline using a loading robot, with one glass being loaded at every takt time (τ). It takes a flow time (π) for a loaded glass to reach the end of the cell where it is unloaded into the unloading cassette located at the I/O port. The unloading cassette departs when it is filled with finished glasses. In unloading the glasses, only one unloading cassette is unloaded at a time. Modeling and Simulation of Discrete-Event Systems No. 23 Chapter 4 – Introduction to Event-based M&S

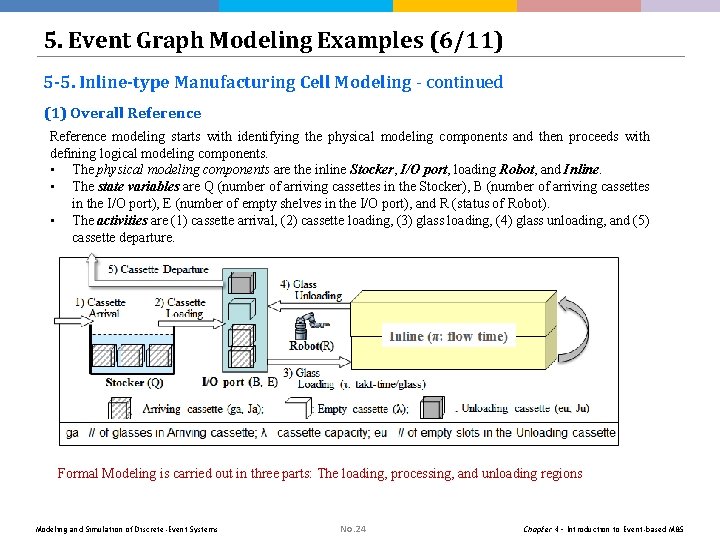
5. Event Graph Modeling Examples (6/11) 5 -5. Inline-type Manufacturing Cell Modeling - continued (1) Overall Reference modeling starts with identifying the physical modeling components and then proceeds with defining logical modeling components. • The physical modeling components are the inline Stocker, I/O port, loading Robot, and Inline. • The state variables are Q (number of arriving cassettes in the Stocker), B (number of arriving cassettes in the I/O port), E (number of empty shelves in the I/O port), and R (status of Robot). • The activities are (1) cassette arrival, (2) cassette loading, (3) glass loading, (4) glass unloading, and (5) cassette departure. Formal Modeling is carried out in three parts: The loading, processing, and unloading regions Modeling and Simulation of Discrete-Event Systems No. 24 Chapter 4 – Introduction to Event-based M&S

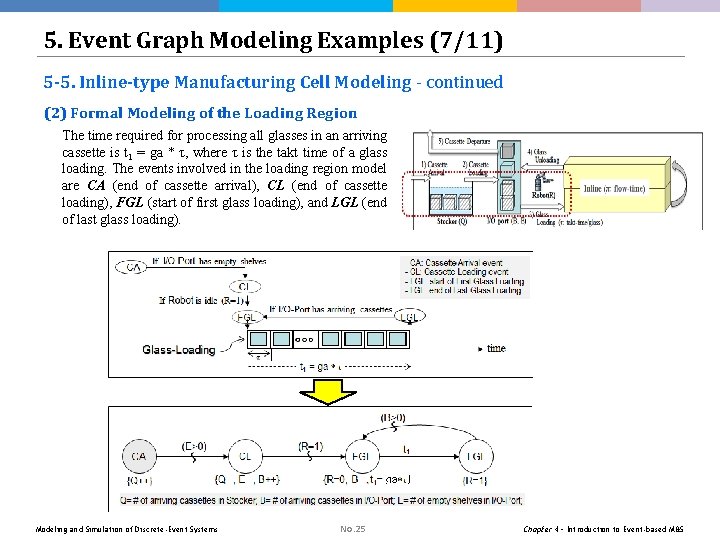
5. Event Graph Modeling Examples (7/11) 5 -5. Inline-type Manufacturing Cell Modeling - continued (2) Formal Modeling of the Loading Region The time required for processing all glasses in an arriving cassette is t 1 = ga * τ, where τ is the takt time of a glass loading. The events involved in the loading region model are CA (end of cassette arrival), CL (end of cassette loading), FGL (start of first glass loading), and LGL (end of last glass loading). Modeling and Simulation of Discrete-Event Systems No. 25 Chapter 4 – Introduction to Event-based M&S

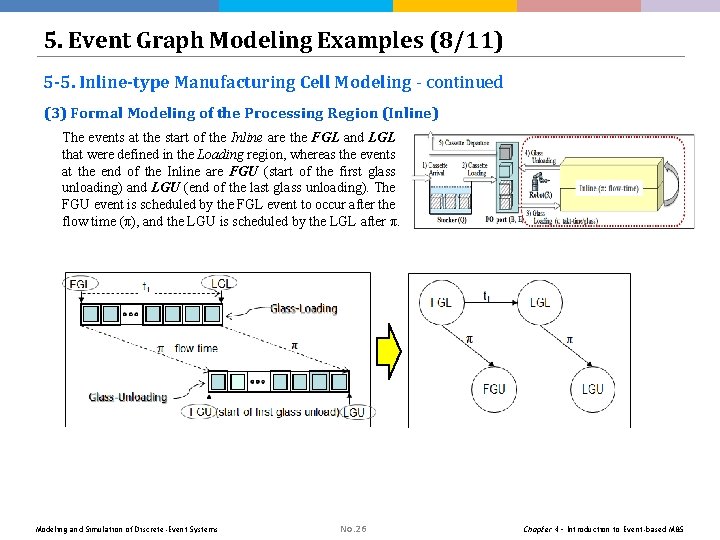
5. Event Graph Modeling Examples (8/11) 5 -5. Inline-type Manufacturing Cell Modeling - continued (3) Formal Modeling of the Processing Region (Inline) The events at the start of the Inline are the FGL and LGL that were defined in the Loading region, whereas the events at the end of the Inline are FGU (start of the first glass unloading) and LGU (end of the last glass unloading). The FGU event is scheduled by the FGL event to occur after the flow time (π), and the LGU is scheduled by the LGL after π. Modeling and Simulation of Discrete-Event Systems No. 26 Chapter 4 – Introduction to Event-based M&S

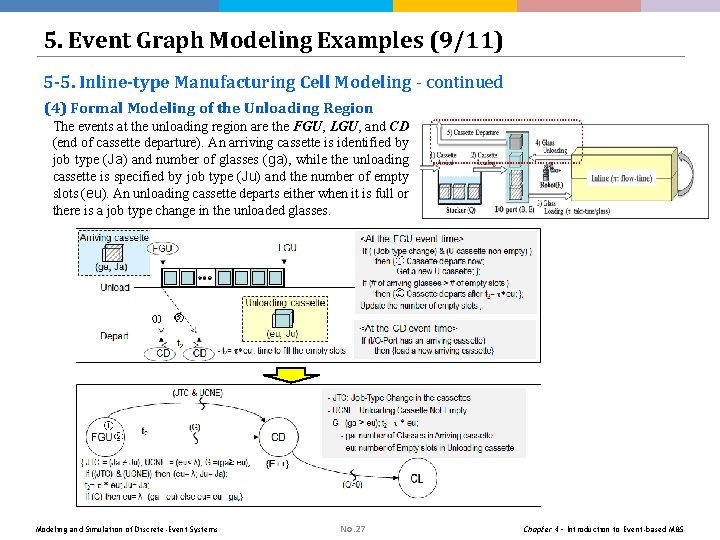
5. Event Graph Modeling Examples (9/11) 5 -5. Inline-type Manufacturing Cell Modeling - continued (4) Formal Modeling of the Unloading Region The events at the unloading region are the FGU, LGU, and CD (end of cassette departure). An arriving cassette is identified by job type (Ja) and number of glasses (ga), while the unloading cassette is specified by job type (Ju) and the number of empty slots (eu). An unloading cassette departs either when it is full or there is a job type change in the unloaded glasses. Modeling and Simulation of Discrete-Event Systems No. 27 Chapter 4 – Introduction to Event-based M&S

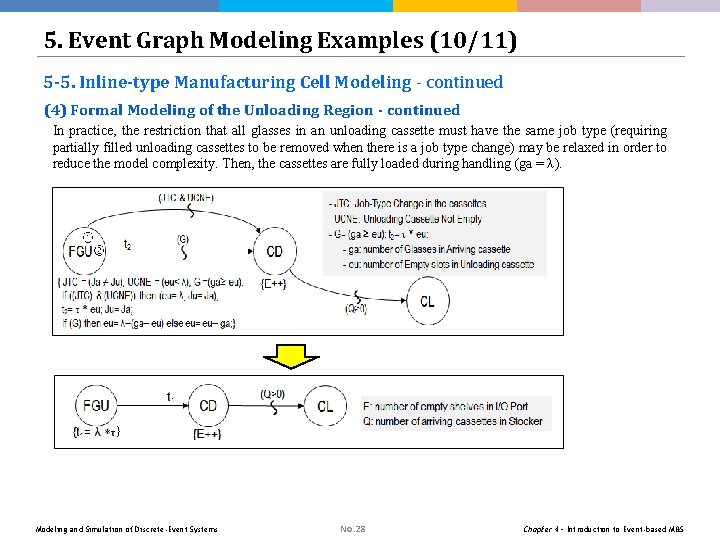
5. Event Graph Modeling Examples (10/11) 5 -5. Inline-type Manufacturing Cell Modeling - continued (4) Formal Modeling of the Unloading Region - continued In practice, the restriction that all glasses in an unloading cassette must have the same job type (requiring partially filled unloading cassettes to be removed when there is a job type change) may be relaxed in order to reduce the model complexity. Then, the cassettes are fully loaded during handling (ga = λ). Modeling and Simulation of Discrete-Event Systems No. 28 Chapter 4 – Introduction to Event-based M&S

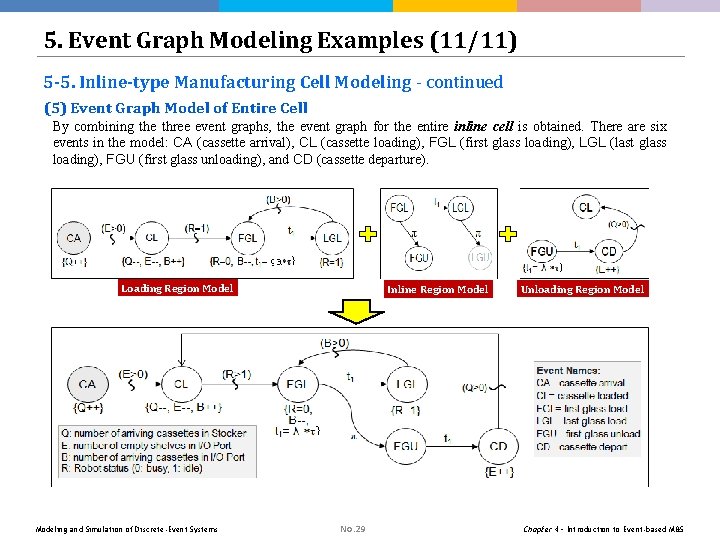
5. Event Graph Modeling Examples (11/11) 5 -5. Inline-type Manufacturing Cell Modeling - continued (5) Event Graph Model of Entire Cell By combining the three event graphs, the event graph for the entire inline cell is obtained. There are six events in the model: CA (cassette arrival), CL (cassette loading), FGL (first glass loading), LGL (last glass loading), FGU (first glass unloading), and CD (cassette departure). Loading Region Modeling and Simulation of Discrete-Event Systems Inline Region Model No. 29 Unloading Region Model Chapter 4 – Introduction to Event-based M&S

6. Execution of Event Graph Models with SIGMA®(0/7) Table of Contents 6 -1. The overall procedure for simulation with SIGMA® 6 -2. Simulation of Conveyor Driven Serial Line with SIGMA Modeling and Simulation of Discrete-Event Systems No. 30 Chapter 4 – Introduction to Event-based M&S

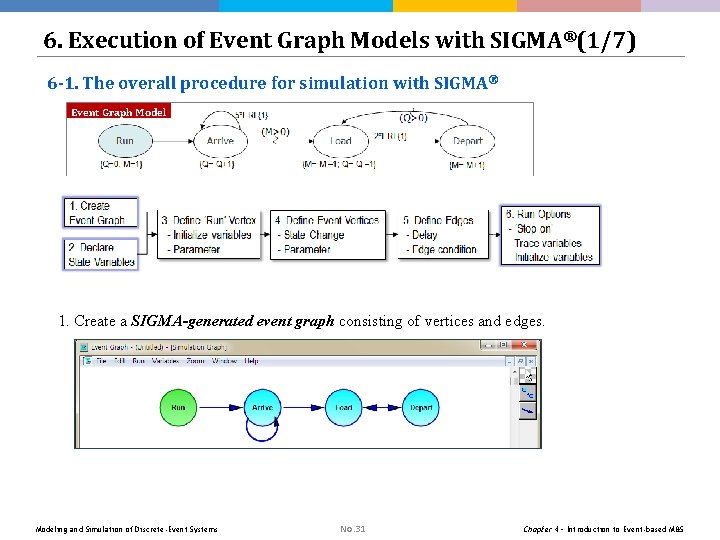
6. Execution of Event Graph Models with SIGMA®(1/7) 6 -1. The overall procedure for simulation with SIGMA® Event Graph Model 1. Create a SIGMA-generated event graph consisting of vertices and edges. Modeling and Simulation of Discrete-Event Systems No. 31 Chapter 4 – Introduction to Event-based M&S

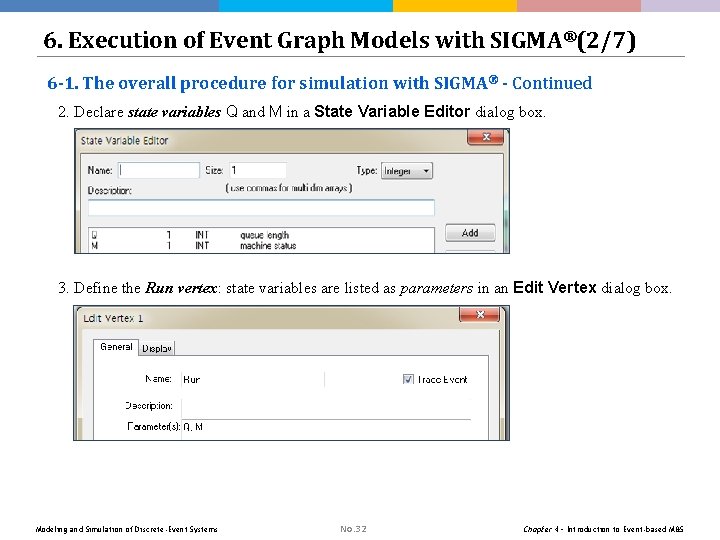
6. Execution of Event Graph Models with SIGMA®(2/7) 6 -1. The overall procedure for simulation with SIGMA® - Continued 2. Declare state variables Q and M in a State Variable Editor dialog box. 3. Define the Run vertex: state variables are listed as parameters in an Edit Vertex dialog box. Modeling and Simulation of Discrete-Event Systems No. 32 Chapter 4 – Introduction to Event-based M&S

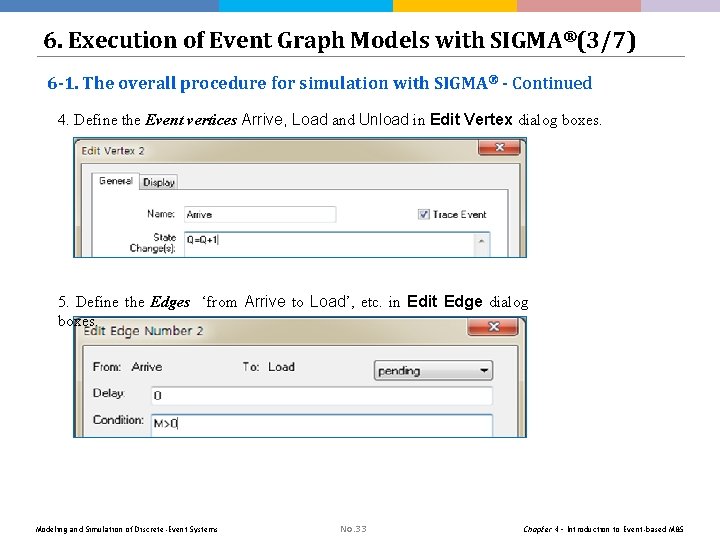
6. Execution of Event Graph Models with SIGMA®(3/7) 6 -1. The overall procedure for simulation with SIGMA® - Continued 4. Define the Event vertices Arrive, Load and Unload in Edit Vertex dialog boxes. 5. Define the Edges ‘from Arrive to Load’, etc. in Edit Edge dialog boxes. Modeling and Simulation of Discrete-Event Systems No. 33 Chapter 4 – Introduction to Event-based M&S

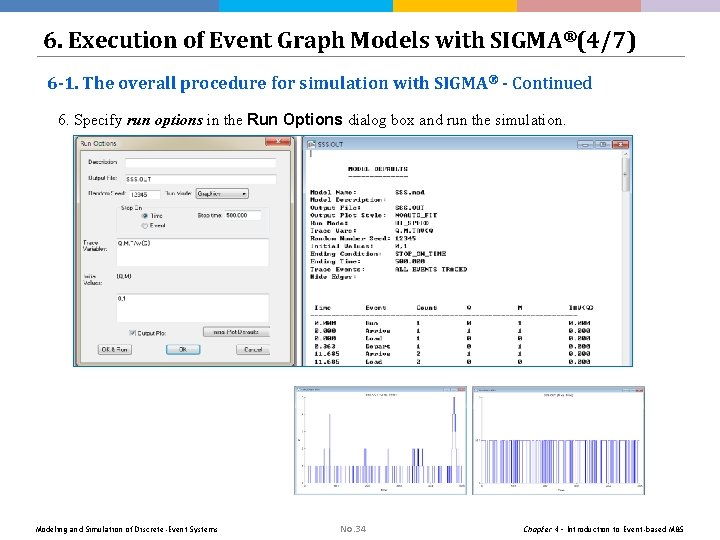
6. Execution of Event Graph Models with SIGMA®(4/7) 6 -1. The overall procedure for simulation with SIGMA® - Continued 6. Specify run options in the Run Options dialog box and run the simulation. Modeling and Simulation of Discrete-Event Systems No. 34 Chapter 4 – Introduction to Event-based M&S

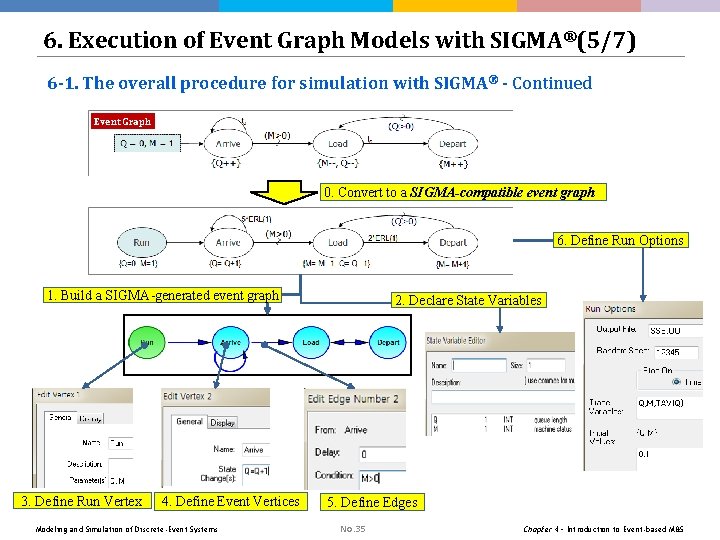
6. Execution of Event Graph Models with SIGMA®(5/7) 6 -1. The overall procedure for simulation with SIGMA® - Continued Event Graph 0. Convert to a SIGMA-compatible event graph 6. Define Run Options 1. Build a SIGMA-generated event graph 3. Define Run Vertex 4. Define Event Vertices Modeling and Simulation of Discrete-Event Systems 2. Declare State Variables 5. Define Edges No. 35 Chapter 4 – Introduction to Event-based M&S

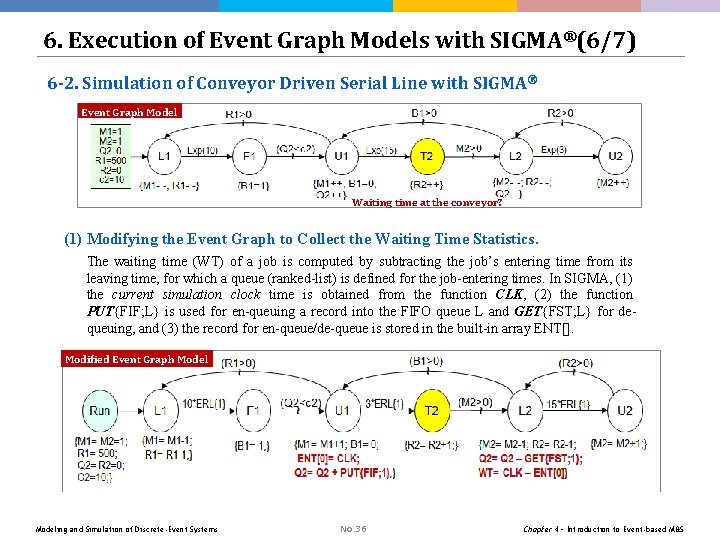
6. Execution of Event Graph Models with SIGMA®(6/7) 6 -2. Simulation of Conveyor Driven Serial Line with SIGMA® Event Graph Model Waiting time at the conveyor? (1) Modifying the Event Graph to Collect the Waiting Time Statistics. The waiting time (WT) of a job is computed by subtracting the job’s entering time from its leaving time, for which a queue (ranked-list) is defined for the job-entering times. In SIGMA, (1) the current simulation clock time is obtained from the function CLK, (2) the function PUT{FIF; L} is used for en-queuing a record into the FIFO queue L and GET{FST; L} for dequeuing, and (3) the record for en-queue/de-queue is stored in the built-in array ENT[]. Modified Event Graph Modeling and Simulation of Discrete-Event Systems No. 36 Chapter 4 – Introduction to Event-based M&S

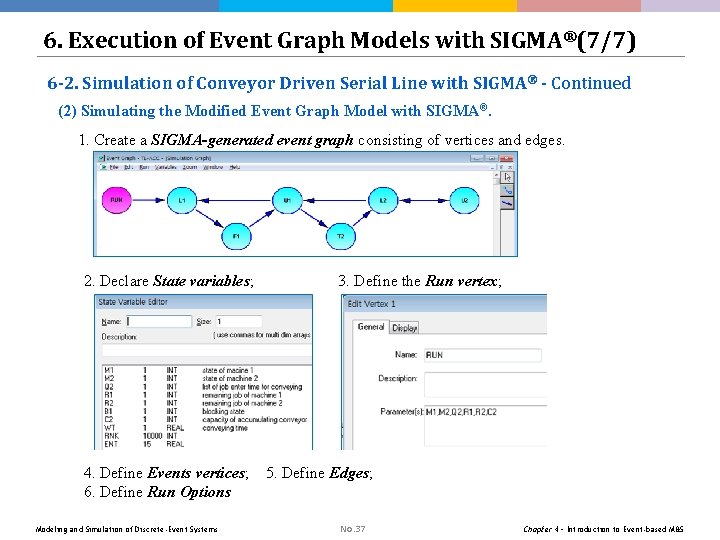
6. Execution of Event Graph Models with SIGMA®(7/7) 6 -2. Simulation of Conveyor Driven Serial Line with SIGMA® - Continued (2) Simulating the Modified Event Graph Model with SIGMA®. 1. Create a SIGMA-generated event graph consisting of vertices and edges. 2. Declare State variables; 4. Define Events vertices; 6. Define Run Options Modeling and Simulation of Discrete-Event Systems 3. Define the Run vertex; 5. Define Edges; No. 37 Chapter 4 – Introduction to Event-based M&S

7. Developing Your Own Event Graph Simulator (0/6) Table of Contents 7 -1. Functions for Handling Events and Managing Queues 7 -2. Functions for Generating Random Variates 7 -3. Event Routines 7 -4. Next-Event Scheduling Algorithm 7 -5. Single Server System Simulator Modeling and Simulation of Discrete-Event Systems No. 38 Chapter 4 – Introduction to Event-based M&S

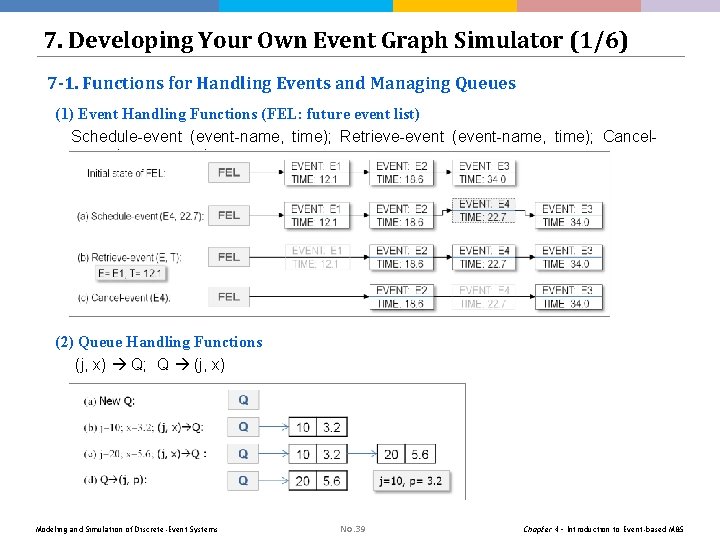
7. Developing Your Own Event Graph Simulator (1/6) 7 -1. Functions for Handling Events and Managing Queues (1) Event Handling Functions (FEL: future event list) Schedule-event (event-name, time); Retrieve-event (event-name, time); Cancelevent (event-name) (2) Queue Handling Functions (j, x) Q; Q (j, x) Modeling and Simulation of Discrete-Event Systems No. 39 Chapter 4 – Introduction to Event-based M&S

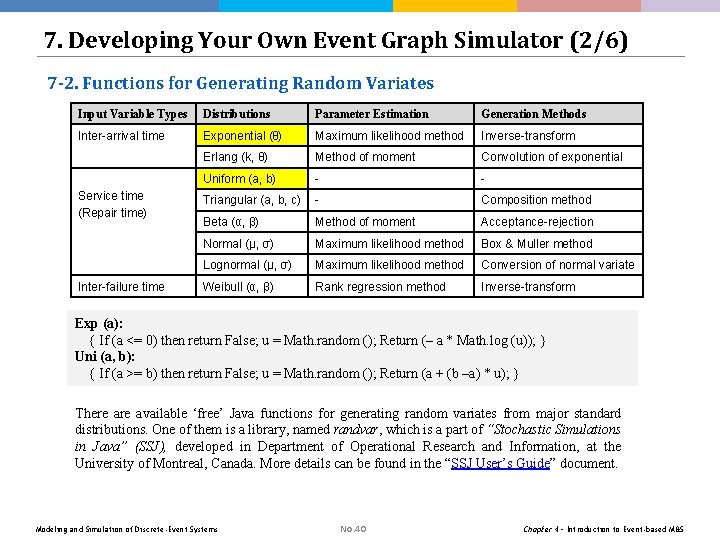
7. Developing Your Own Event Graph Simulator (2/6) 7 -2. Functions for Generating Random Variates Input Variable Types Distributions Parameter Estimation Generation Methods Inter-arrival time Exponential (θ) Maximum likelihood method Inverse-transform Erlang (k, θ) Method of moment Convolution of exponential Uniform (a, b) - - Triangular (a, b, c) - Composition method Beta (α, β) Method of moment Acceptance-rejection Normal (μ, σ) Maximum likelihood method Box & Muller method Lognormal (μ, σ) Maximum likelihood method Conversion of normal variate Weibull (α, β) Rank regression method Inverse-transform Service time (Repair time) Inter-failure time Exp (a): { If (a <= 0) then return False; u = Math. random (); Return (– a * Math. log (u)); } Uni (a, b): { If (a >= b) then return False; u = Math. random (); Return (a + (b –a) * u); } There available ‘free’ Java functions for generating random variates from major standard distributions. One of them is a library, named randvar, which is a part of “Stochastic Simulations in Java” (SSJ), developed in Department of Operational Research and Information, at the University of Montreal, Canada. More details can be found in the “SSJ User’s Guide” document. Modeling and Simulation of Discrete-Event Systems No. 40 Chapter 4 – Introduction to Event-based M&S

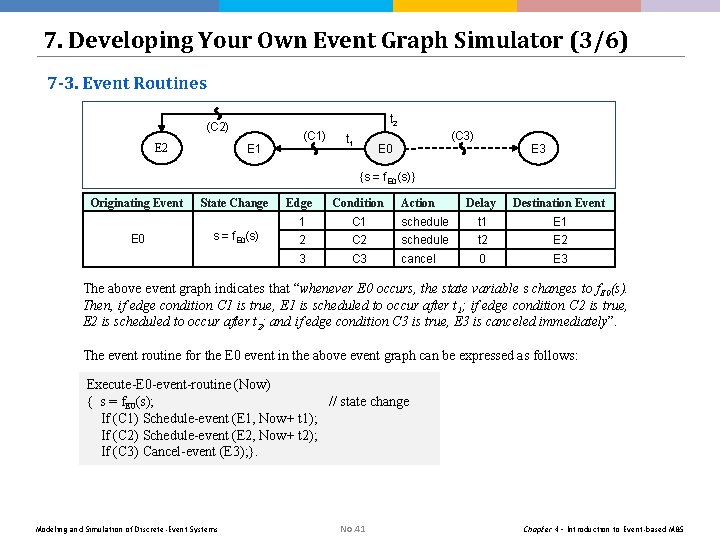
7. Developing Your Own Event Graph Simulator (3/6) 7 -3. Event Routines t 2 (C 2) E 2 E 1 (C 1) t 1 (C 3) E 0 E 3 {s = f. E 0(s)} Originating Event E 0 State Change s = f. E 0(s) Edge Condition 1 C 1 2 3 Action Delay Destination Event schedule t 1 E 1 C 2 schedule t 2 E 2 C 3 cancel 0 E 3 The above event graph indicates that “whenever E 0 occurs, the state variable s changes to f. E 0(s). Then, if edge condition C 1 is true, E 1 is scheduled to occur after t 1; if edge condition C 2 is true, E 2 is scheduled to occur after t 2; and if edge condition C 3 is true, E 3 is canceled immediately”. The event routine for the E 0 event in the above event graph can be expressed as follows: Execute-E 0 -event-routine (Now) { s = f. E 0(s); // state change If (C 1) Schedule-event (E 1, Now+ t 1); If (C 2) Schedule-event (E 2, Now+ t 2); If (C 3) Cancel-event (E 3); }. Modeling and Simulation of Discrete-Event Systems No. 41 Chapter 4 – Introduction to Event-based M&S

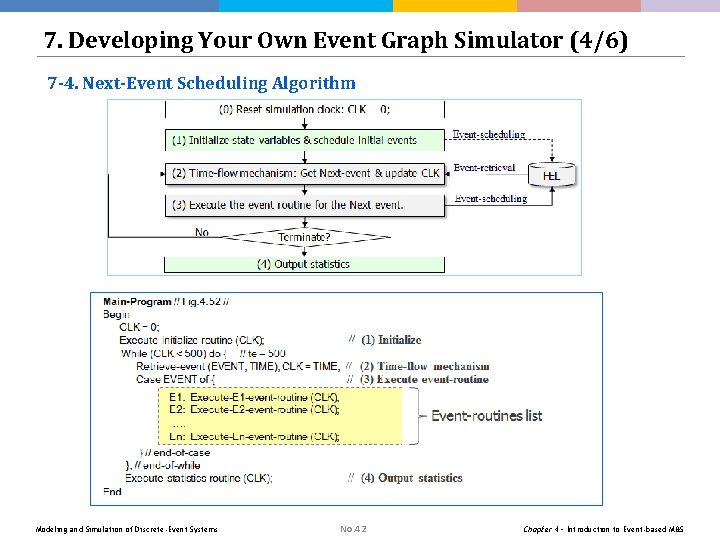
7. Developing Your Own Event Graph Simulator (4/6) 7 -4. Next-Event Scheduling Algorithm Modeling and Simulation of Discrete-Event Systems No. 42 Chapter 4 – Introduction to Event-based M&S

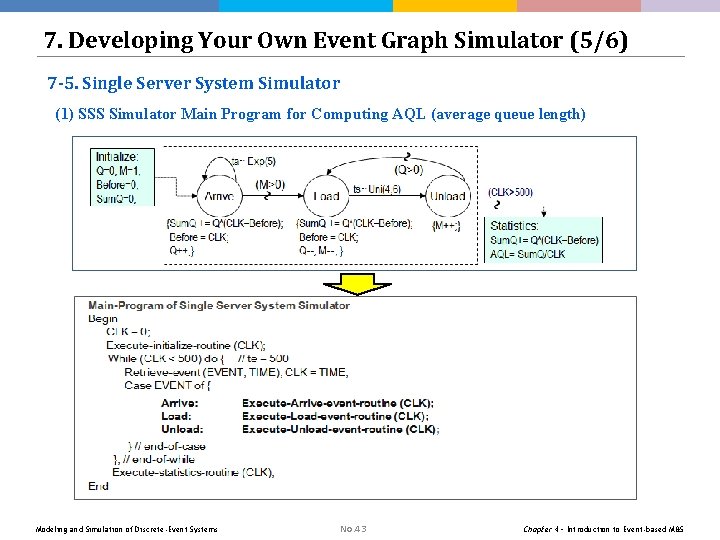
7. Developing Your Own Event Graph Simulator (5/6) 7 -5. Single Server System Simulator (1) SSS Simulator Main Program for Computing AQL (average queue length) Modeling and Simulation of Discrete-Event Systems No. 43 Chapter 4 – Introduction to Event-based M&S

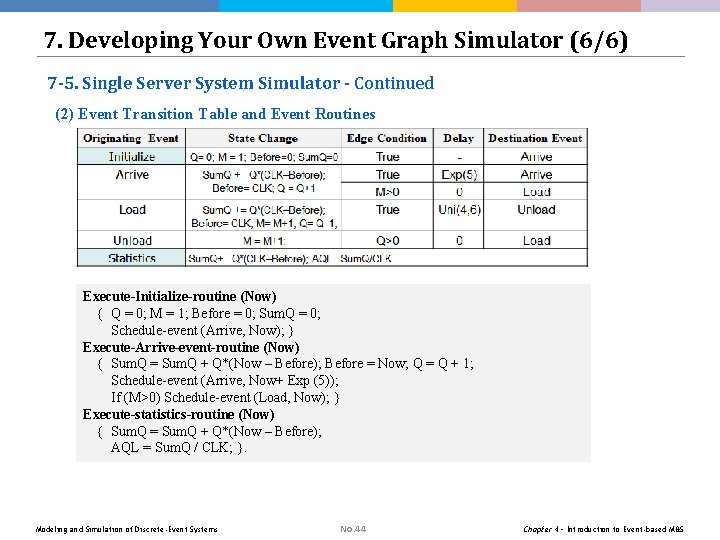
7. Developing Your Own Event Graph Simulator (6/6) 7 -5. Single Server System Simulator - Continued (2) Event Transition Table and Event Routines Execute-Initialize-routine (Now) { Q = 0; M = 1; Before = 0; Sum. Q = 0; Schedule-event (Arrive, Now); } Execute-Arrive-event-routine (Now) { Sum. Q = Sum. Q + Q*(Now – Before); Before = Now; Q = Q + 1; Schedule-event (Arrive, Now+ Exp (5)); If (M>0) Schedule-event (Load, Now); } Execute-statistics-routine (Now) { Sum. Q = Sum. Q + Q*(Now – Before); AQL = Sum. Q / CLK; }. Modeling and Simulation of Discrete-Event Systems No. 44 Chapter 4 – Introduction to Event-based M&S