Chapter 4 Graphing Linear Equations and Functions 4











- Slides: 14

Chapter 4 Graphing Linear Equations and Functions 4. 3 Quick Graphs Using Intercepts

Quicker ways to graph In 4. 2 you used a table of values to plot points, and then you drew a line through the points. But how many points do you need to figure out exactly where the line goes on the graph? 2!!

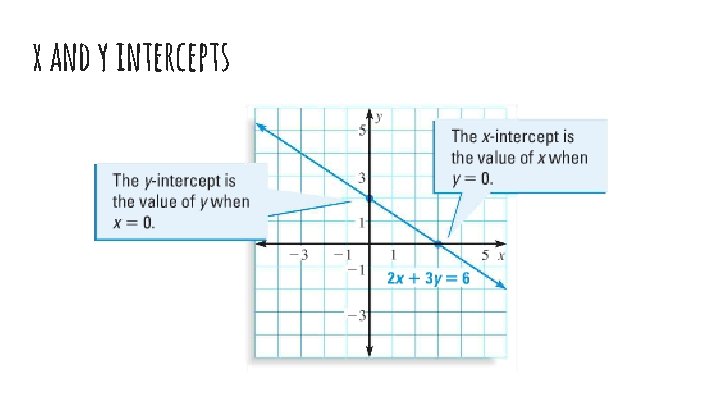
Quicker Ways to Graph The quickest two points to figure out are the intercepts. x-intercept : is the x-coordinate of a point where the graph crosses the x-axis y-intercept : is the y-coordinate of a point whre a graph crosses the y-axis

x and y intercepts

Finding the Intercepts x-intercept: Find the x-intercept by making y=0 and solving for x. Find the y-intercept by making x=0 and solving for y.

Finding Intercepts Find the x-intercept and the y-intercept of the graph of the equation 2 x + 3 y = 6. To find the x-intercept, let y=0. To find the y-intercept, let x=0. 2 x + 3 y = 6 2 x + 3(0) = 6 2 x + 3 y = 6 2(0) + 3 y = 6 Solve for x. Solve for y. 2 x + 3(0) = 6 2 x + 0 = 6 2 x = 6 x = 3 2(0) + 3 y = 6 0 + 3 y = 6 y = 2

Find the x and y intercepts of 4 x + 2 y = 8 Answer: x-intercept = 2, y-intercept = 4

Making a quick graph Step 1: Find the intercepts Step 2: Plot the intercepts Step 3: Draw a line through the points.

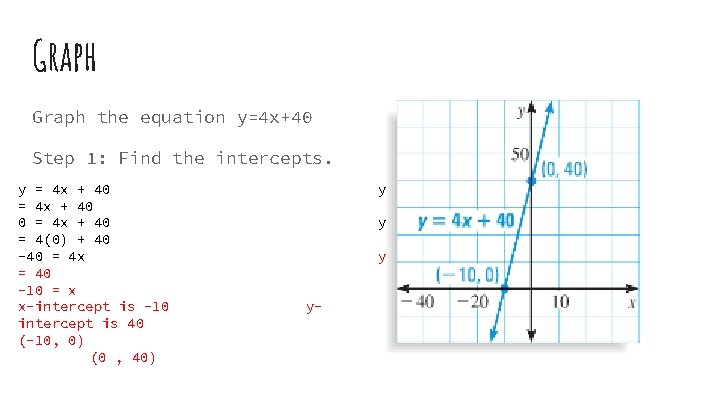
Graph the equation y=4 x+40 Step 1: Find the intercepts. y = 4 x + 40 0 = 4 x + 40 = 4(0) + 40 -40 = 4 x = 40 -10 = x x-intercept is -10 intercept is 40 (-10, 0) (0 , 40) y y-

Word Problems!!! Step 1: Figure out what they are asking. Step 2: Write down all known information. Step 3: Create a Verbal Model. Step 4: Create an algebraic model. Step 5: Solve.

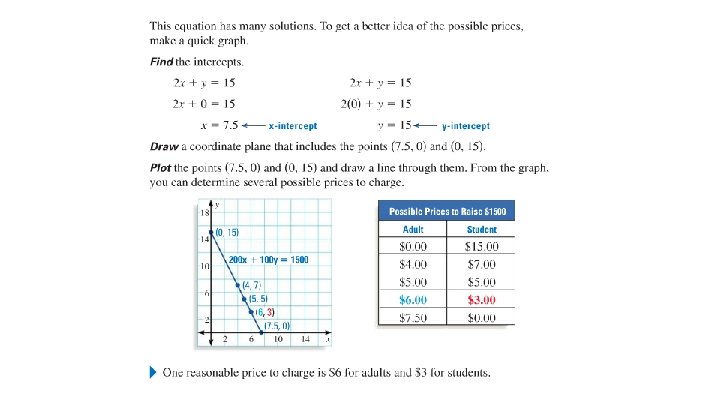
You are organizing the annual spaghetti dinner to raise funds for a zoo. Your goal is to sell $1500 worth of tickets. Assuming 200 adults and 100 students will attend the dinner, how much should you charge for an adult ticket and for a student ticket? Step 1: What are they asking? How much should adult tickets cost, and how much should student tickets cost. Step 2: Write down all known information:

Step 3: Create a verbal model. Step 4: Create an algebraic model. Step 5: Solve. We can see that we now have a linear equation, and we know that this has infinite number of possible solutions for x and y!


Homework 4. 3 # 15, 37, 45, 47, 49, 51, 55, 63