CHAPTER 4 FREQUENCY RESPONSE IN AC CIRCUIT PART

CHAPTER 4: FREQUENCY RESPONSE IN AC CIRCUIT -PART ISAIDATUL SHEMA BINTI SAAD 019 -4249348 / 016 -6651449 (Whats. App) JABATAN TEKNOLOGI KEJURUTERAAN ELEKTRIK , FAKULTI TEKNOLOGI KEJURUTERAAN , ARAS 1 BLOK S 2 (bawah BK 5), KAMPUS UNICITI ALAM , UNIVERSITI MALAYSIA PERLIS. PLT 201 – ELECTRIC CIRCUIT THEORY II

What to learn in this chapter? Introduction to frequency response Transfer Function Bode Plot Series Resonance Parallel Resonance Passive Filter PLT 201 – ELECTRIC CIRCUIT

4. 1 INTRODUCTION q Frequency response of a circuit define as • “variation in its behavior with change in signal frequency” Also considered as • “variation of the gain and phase with frequency” PLT 201 – ELECTRIC CIRCUIT

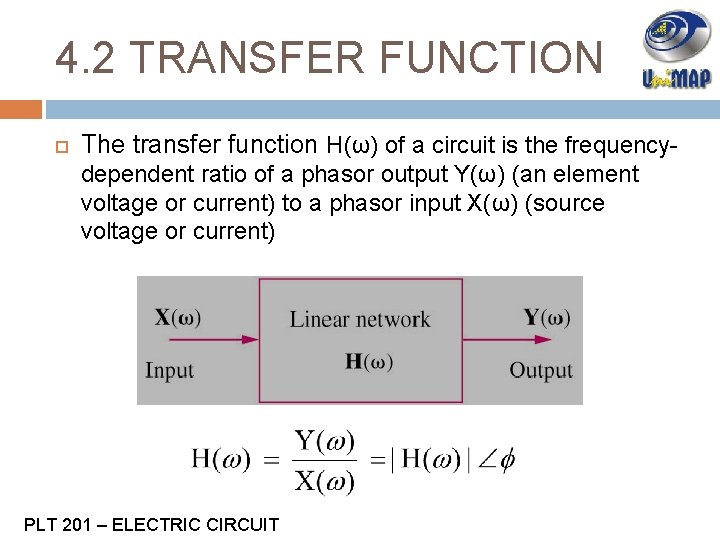
4. 2 TRANSFER FUNCTION The transfer function H(ω) of a circuit is the frequencydependent ratio of a phasor output Y(ω) (an element voltage or current) to a phasor input X(ω) (source voltage or current) PLT 201 – ELECTRIC CIRCUIT

4. 2 CONT… Four possible transfer functions: PLT 201 – ELECTRIC CIRCUIT

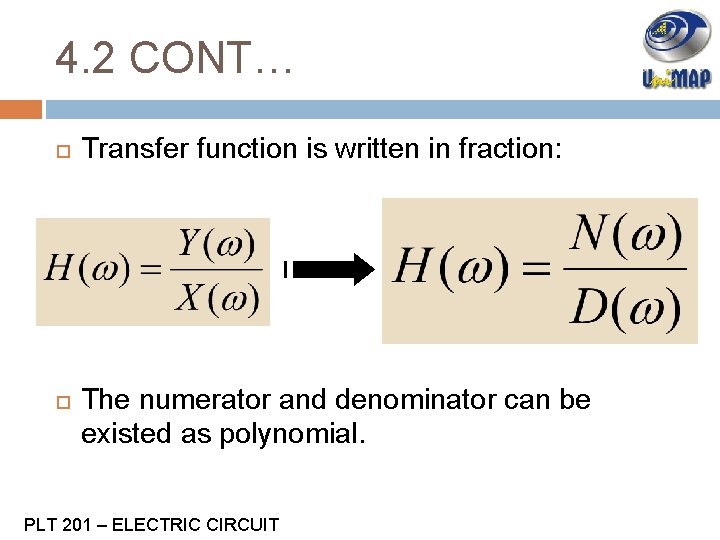
4. 2 CONT… Transfer function is written in fraction: The numerator and denominator can be existed as polynomial. PLT 201 – ELECTRIC CIRCUIT

4. 2 CONT… The roots of numerator known as ZEROS of H(ω) when N(ω) = 0 (represented as jω=z 1, z 2, …. . ) The roots of denominator known as POLES of H(ω) when D(ω) = 0 (represented as jω=p 1, p 2, …. . ) Complex s-plane is used to plot poles and zeros. PLT 201 – ELECTRIC CIRCUIT

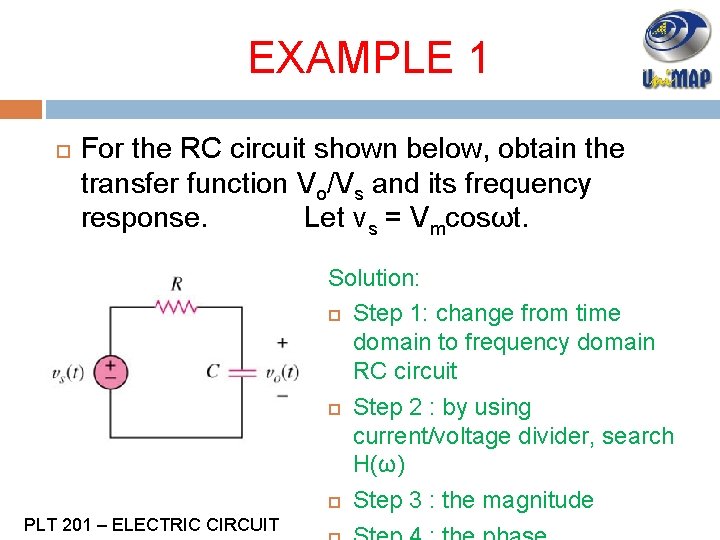
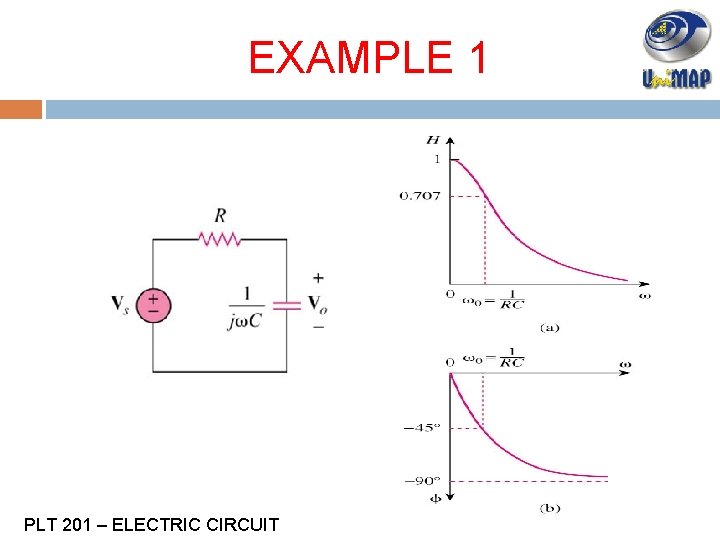
EXAMPLE 1 For the RC circuit shown below, obtain the transfer function Vo/Vs and its frequency response. Let vs = Vmcosωt. Solution: Step 1: change from time domain to frequency domain RC circuit Step 2 : by using current/voltage divider, search H(ω) Step 3 : the magnitude PLT 201 – ELECTRIC CIRCUIT

EXAMPLE 1 PLT 201 – ELECTRIC CIRCUIT

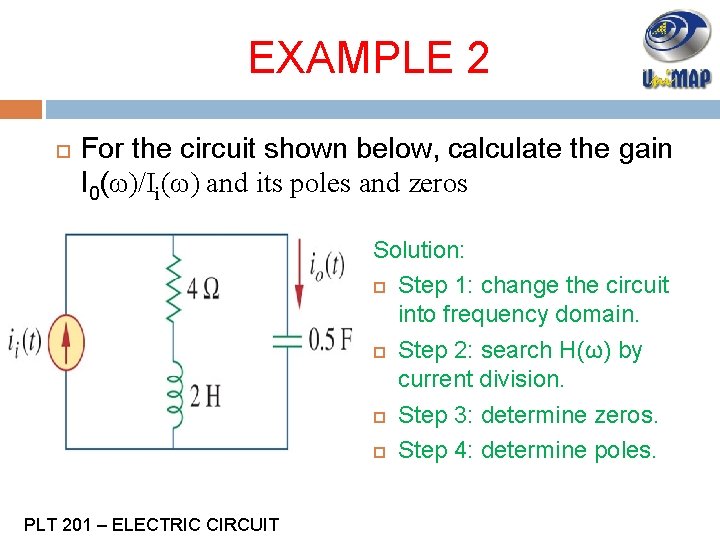
EXAMPLE 2 For the circuit shown below, calculate the gain I 0(ω)/Ii(ω) and its poles and zeros Solution: Step 1: change the circuit into frequency domain. Step 2: search H(ω) by current division. Step 3: determine zeros. Step 4: determine poles. PLT 201 – ELECTRIC CIRCUIT

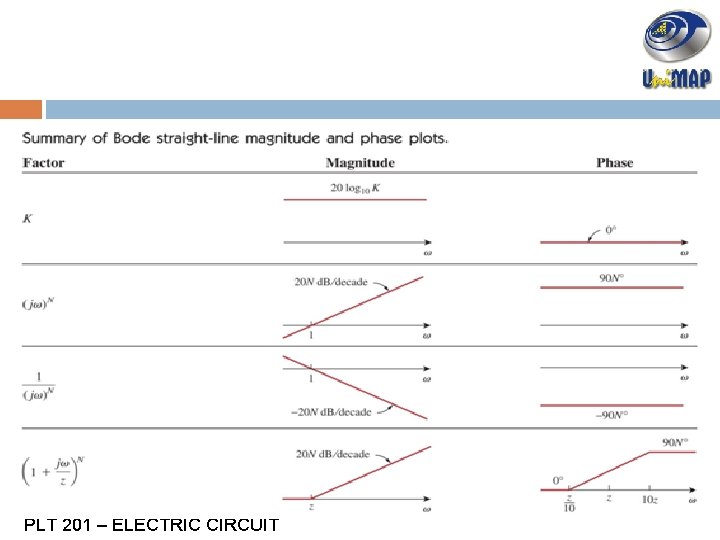
4. 3 BODE PLOT Bode plot are semilog plots of the magnitude (in decibels) and phase (in degrees) of a transfer function versus frequency. PLT 201 – ELECTRIC CIRCUIT

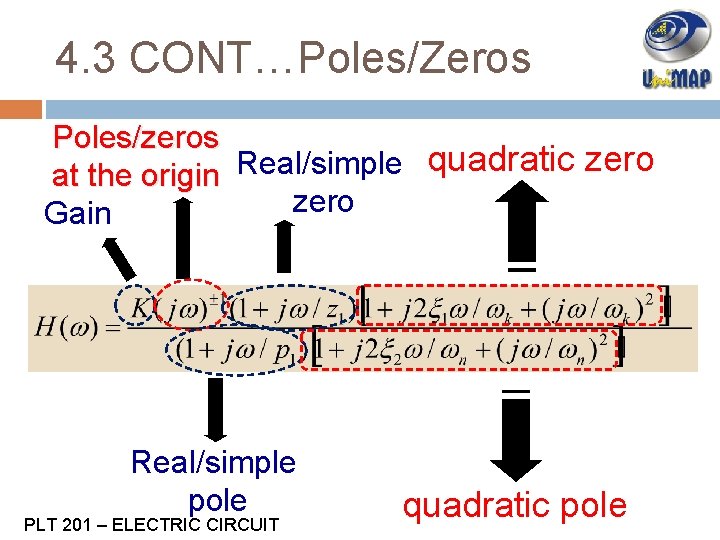
4. 3 CONT…Poles/Zeros Poles/zeros quadratic zero Real/simple at the origin zero Gain Real/simple pole PLT 201 – ELECTRIC CIRCUIT quadratic pole

4. 3 CONT…location of poles/zeros Poles/Zeros at the origin: Poles/Zeros that are located at 0 Real Poles/Zeros : Poles/Zeros that are located at real axis: (-1, -2, 1, 2, 10, etc) Quadratic Poles/Zeros : Poles/Zeros that are not located at imaginary or real axis: (-1+j 2, 2+j 5, 3 -j 3, etc) PLT 201 – ELECTRIC CIRCUIT

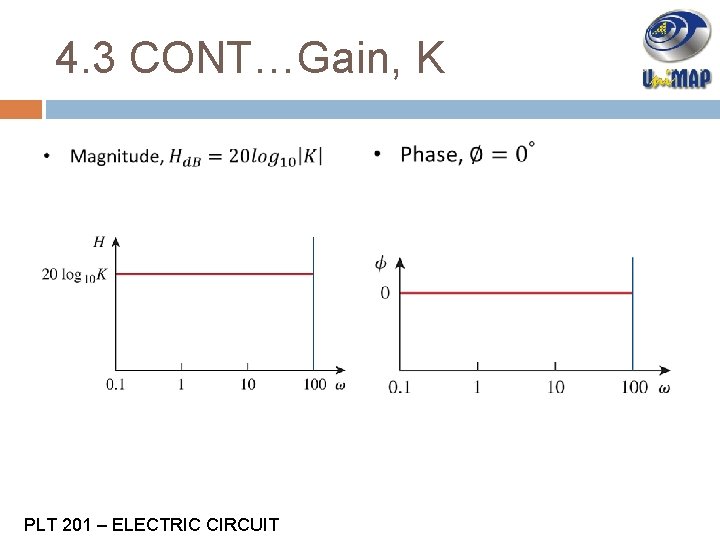
4. 3 CONT…Gain, K PLT 201 – ELECTRIC CIRCUIT

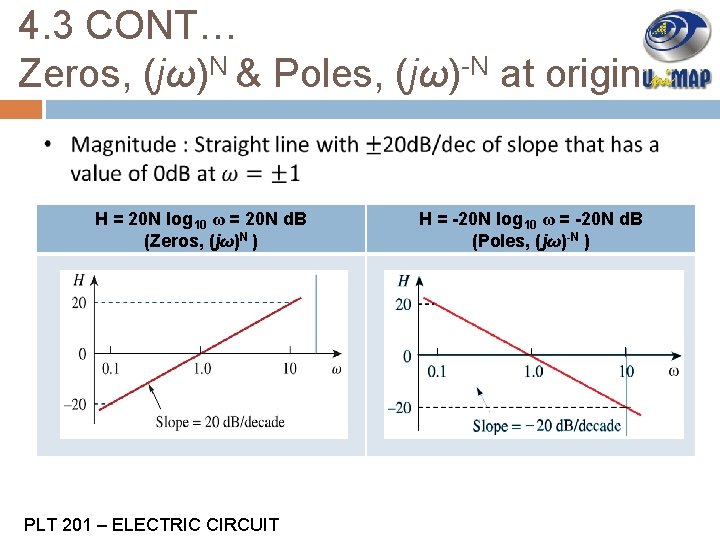
4. 3 CONT… Zeros, (jω)N & Poles, (jω)-N at origin H = 20 N log 10 ω = 20 N d. B (Zeros, (jω)N ) PLT 201 – ELECTRIC CIRCUIT H = -20 N log 10 ω = -20 N d. B (Poles, (jω)-N )

4. 3 CONT… Zeros, (jω)N & Poles, (jω)-N at origin Phase, ϕ = 90°N (Zeros, (jω)N ) PLT 201 – ELECTRIC CIRCUIT Phase, ϕ = -90°N (Poles, (jω)-N )

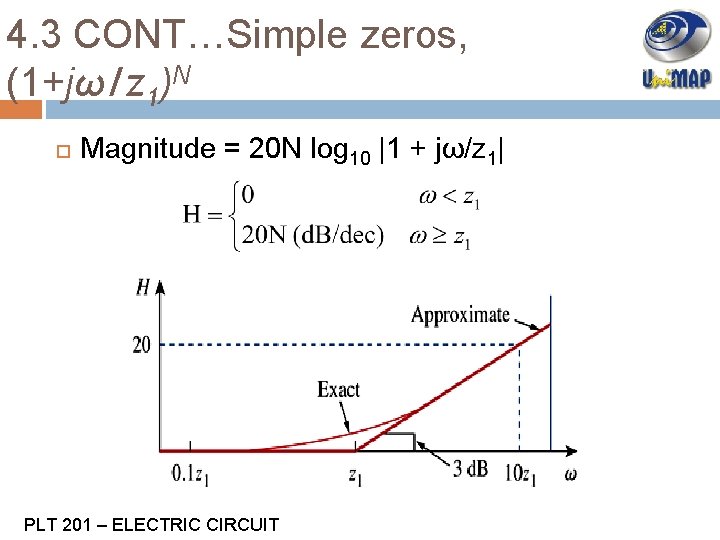
4. 3 CONT…Simple zeros, (1+jω/z 1)N Magnitude = 20 N log 10 |1 + jω/z 1| PLT 201 – ELECTRIC CIRCUIT

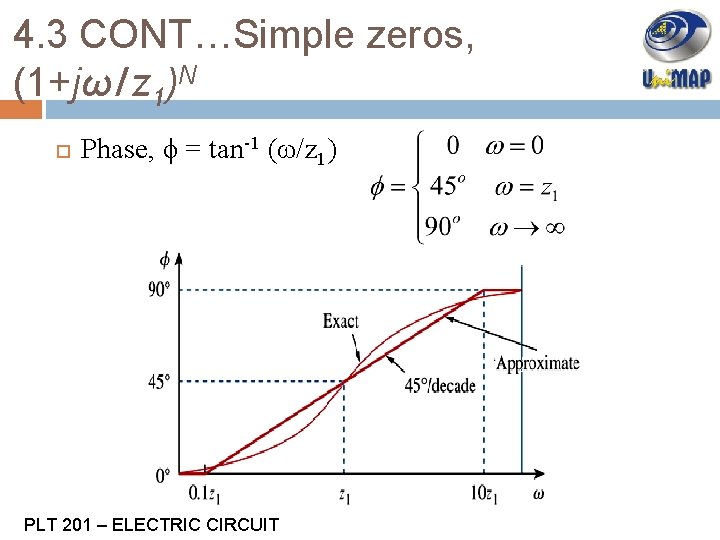
4. 3 CONT…Simple zeros, (1+jω/z 1)N Phase, ϕ = tan-1 (ω/z 1) PLT 201 – ELECTRIC CIRCUIT

4. 3 CONT…Simple Poles, (1+jω/z 1)-N Magnitude = -20 N log 10 |1 + jω/z 1 | PLT 201 – ELECTRIC CIRCUIT

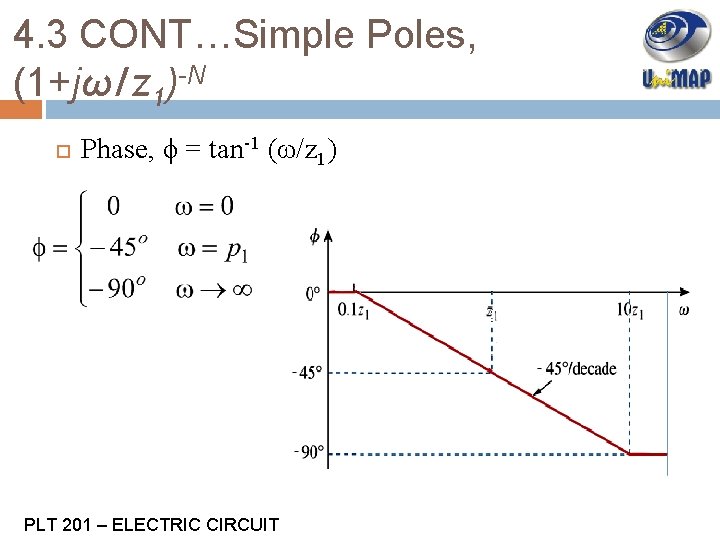
4. 3 CONT…Simple Poles, (1+jω/z 1)-N Phase, ϕ = tan-1 (ω/z 1) PLT 201 – ELECTRIC CIRCUIT

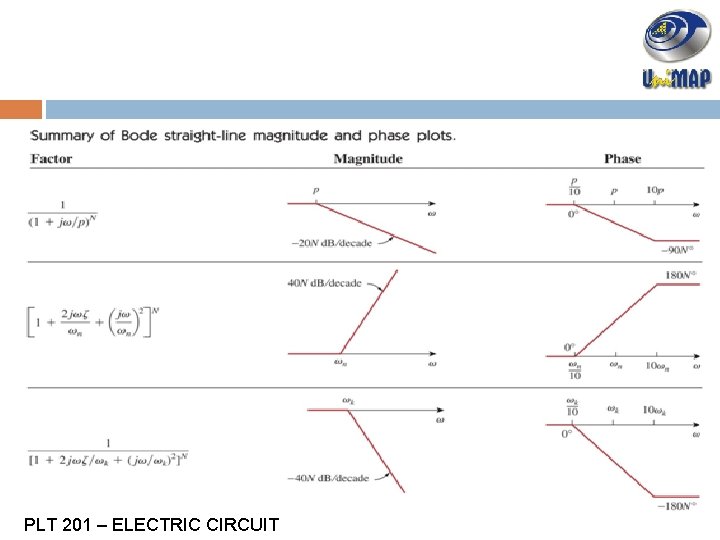
4. 3 CONT…QUADRATIC ZEROS, [1+j 2ζ 1ω/ωn+(jω/ωn)2] N Magnitude = PLT 201 – ELECTRIC CIRCUIT

4. 3 CONT…QUADRATIC ZEROS, [1+j 2ζ 1ω/ωn+(jω/ωn)2] N Phase = PLT 201 – ELECTRIC CIRCUIT

4. 3 CONT…QUADRATIC POLES, [1+j 2ζ 1ω/ωk+(jω/ωk)2] -N Magnitude = PLT 201 – ELECTRIC CIRCUIT

4. 3 CONT…QUADRATIC POLES, [1+j 2ζ 1ω/ωk+(jω/ωk)2] -N Phase = PLT 201 – ELECTRIC CIRCUIT

HOW TO DRAW A BODE PLOT While drawing the bode plot, every factor (i. e zeros/poles) were drawed separately on the semilog graph. Finally, all of the factor are combined to form the answer. PLT 201 – ELECTRIC CIRCUIT

EXAMPLE 3 Draw a Bode Plot for the given transfer function below: PLT 201 – ELECTRIC CIRCUIT

Guidelines solution for Example 3 Step 1: make the transfer function as general equation Step 2: change the general equation into the magnitude of transfer function Step 3: phase of transfer function Step 4: magnitude plot guidance Step 5: Draw the magnitude Plot Step 6: Phase plot guidance Draw the Phase plot PLT 201 – ELECTRIC CIRCUIT

SOLUTION EXAMPLE 3 Step 1: make the transfer function as general equation PLT 201 – ELECTRIC CIRCUIT

SOLUTION EXAMPLE 3 Step 2: change the general equation into the magnitude of transfer function Note: PLT 201 – ELECTRIC CIRCUIT

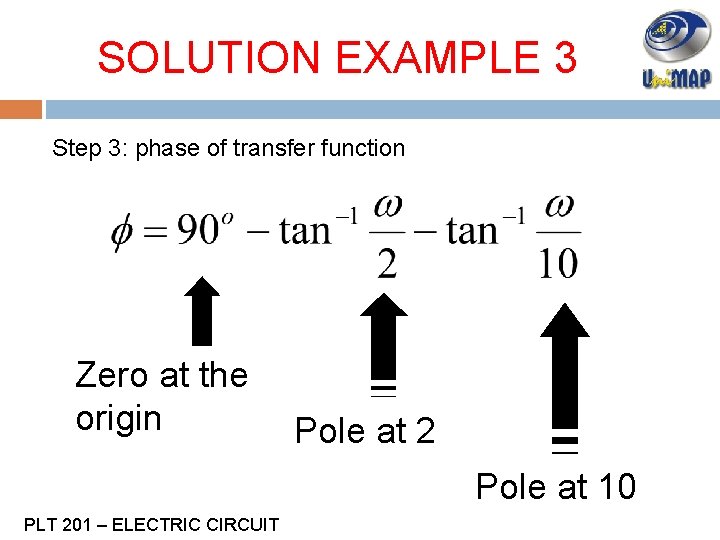
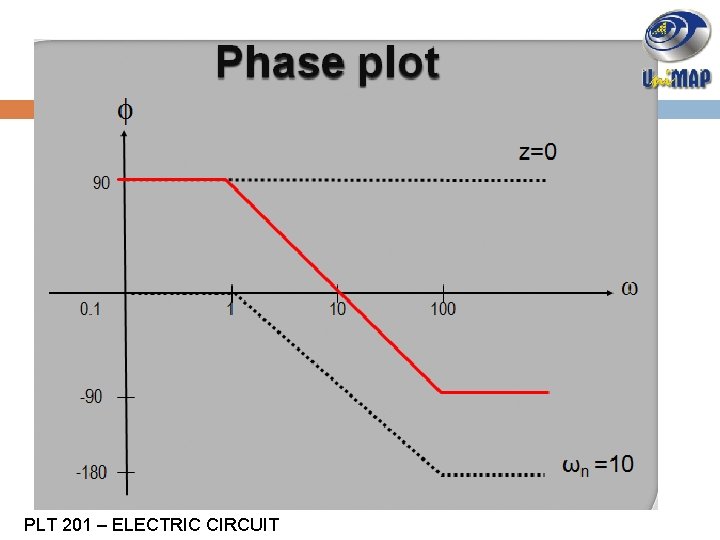
SOLUTION EXAMPLE 3 Step 3: phase of transfer function Zero at the origin Pole at 2 Pole at 10 PLT 201 – ELECTRIC CIRCUIT

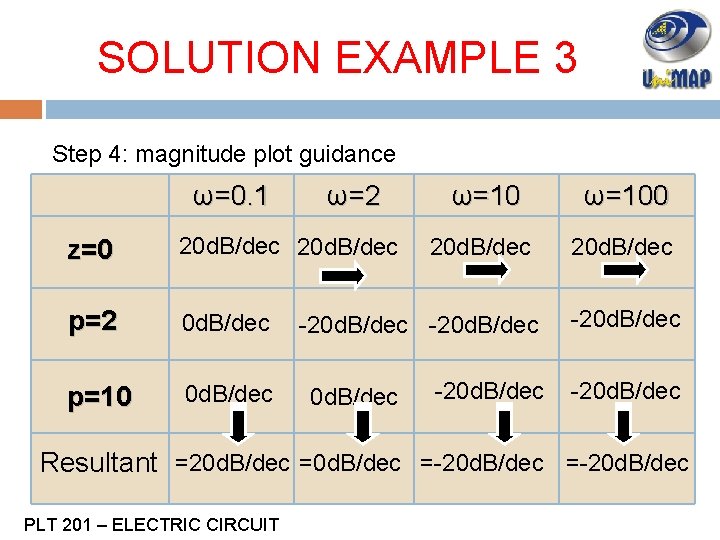
SOLUTION EXAMPLE 3 Step 4: magnitude plot guidance ω=0. 1 ω=2 z=0 20 d. B/dec p=2 0 d. B/dec p=10 0 d. B/dec ω=100 20 d. B/dec -20 d. B/dec Resultant =20 d. B/dec =-20 d. B/dec PLT 201 – ELECTRIC CIRCUIT

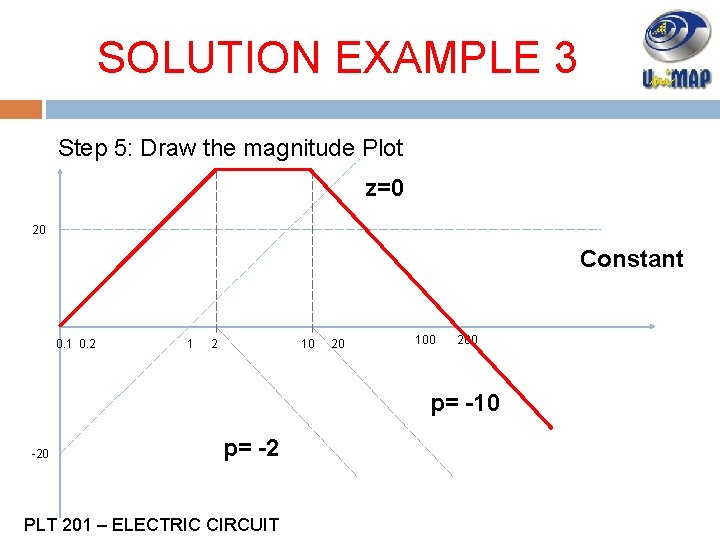
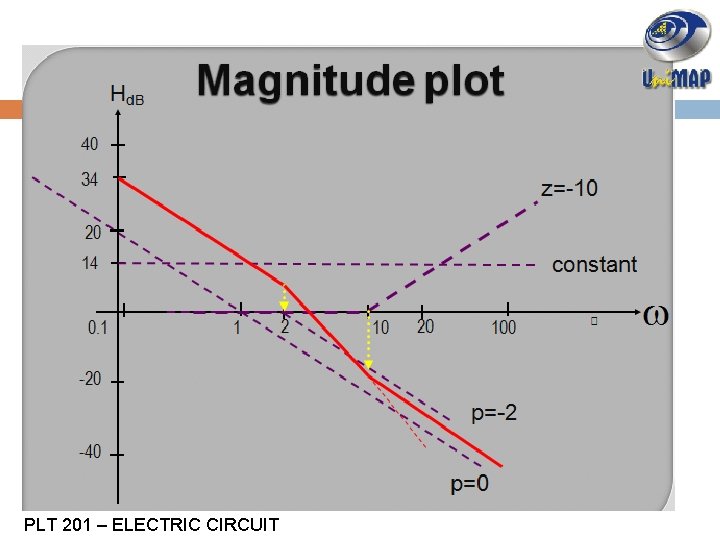
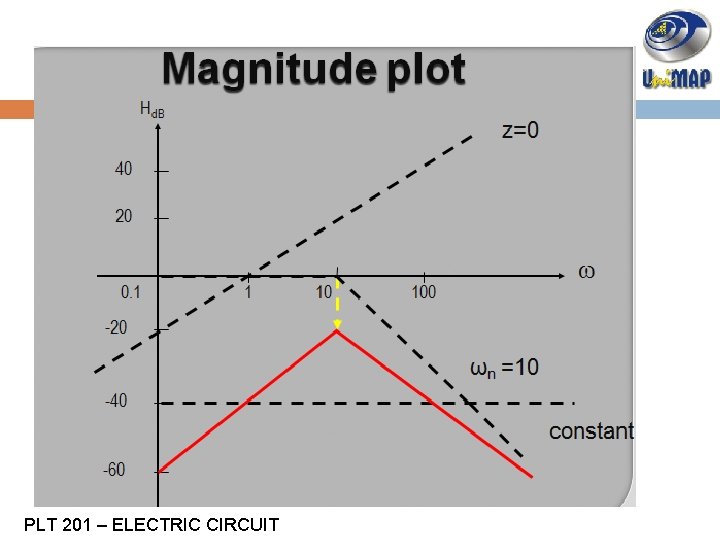
SOLUTION EXAMPLE 3 Step 5: Draw the magnitude Plot z=0 20 Constant 0. 1 0. 2 10 20 100 200 p= -10 -20 p= -2 PLT 201 – ELECTRIC CIRCUIT

SOLUTION EXAMPLE 3 Step 6: Phase plot guidance ω=0. 2 ω=1 ω=20 ω=100 z=0 90º 90º 90º p=2 0º/dec -90 º p=10 0º/dec Resultant 90º -45º/dec 0º/dec -45º/dec -90º/dec -45º/dec -90º Add all of the lines that having a slope only PLT 201 – ELECTRIC CIRCUIT

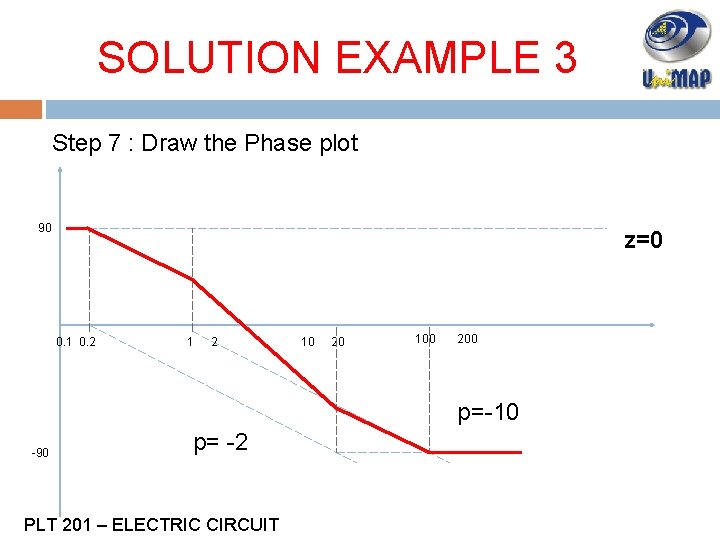
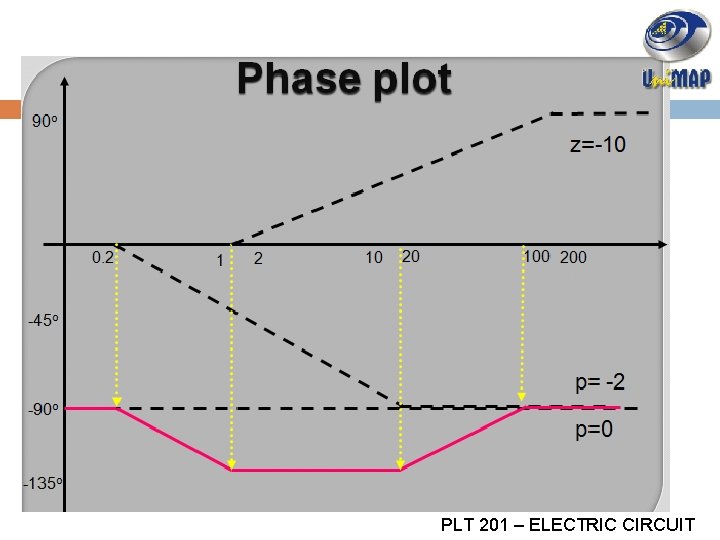
SOLUTION EXAMPLE 3 Step 7 : Draw the Phase plot 90 z=0 0. 1 0. 2 10 20 100 200 p=-10 -90 p= -2 PLT 201 – ELECTRIC CIRCUIT

EXAMPLE 4 Draw the bode plot for the given transfer function as below: PLT 201 – ELECTRIC CIRCUIT

PLT 201 – ELECTRIC CIRCUIT

PLT 201 – ELECTRIC CIRCUIT

EXAMPLE 5 Draw the Bode Plot for the given transfer function as below: PLT 201 – ELECTRIC CIRCUIT

PLT 201 – ELECTRIC CIRCUIT

PLT 201 – ELECTRIC CIRCUIT

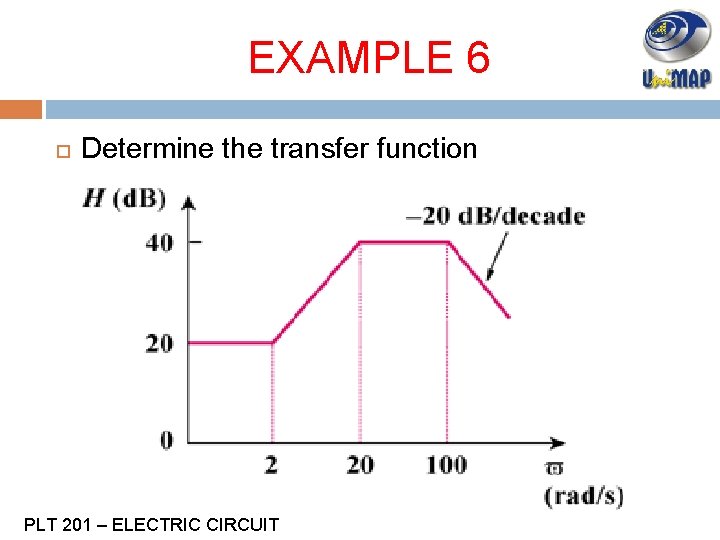
EXAMPLE 6 Determine the transfer function PLT 201 – ELECTRIC CIRCUIT

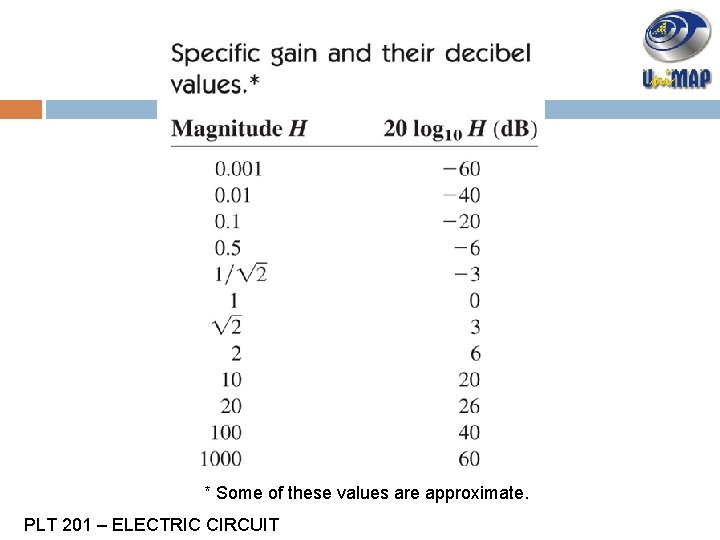
* Some of these values are approximate. PLT 201 – ELECTRIC CIRCUIT

PLT 201 – ELECTRIC CIRCUIT

PLT 201 – ELECTRIC CIRCUIT