Chapter 4 Fourier Series Transforms Basic Idea notes

Chapter 4 Fourier Series & Transforms

Basic Idea notes

Taylor Series • Complex signals are often broken into simple pieces • Signal requirements – Can be expressed into simpler problems – The first few terms can approximate the signal • Example: The Taylor series of a real or complex function ƒ(x) is the power series • http: //upload. wikimedia. org/wikipedia/commons/6/62/Exp_series. gif

Square Wave S(t)=sin(2 pft) S(t)=1/3[sin(2 p(3 f)t)] S(t)= 4/p{sin(2 pft) +1/3[sin(2 p(3 f)t)]} Fourier Expansion

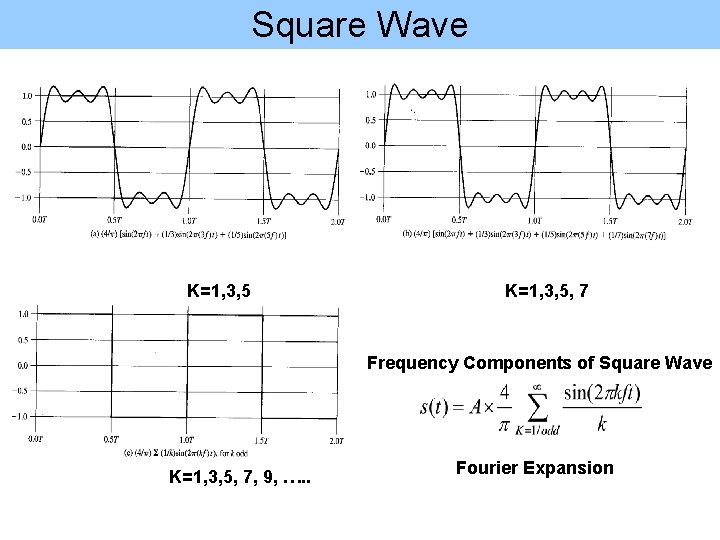
Square Wave K=1, 3, 5, 7 Frequency Components of Square Wave K=1, 3, 5, 7, 9, …. . Fourier Expansion

Periodic Signals • A Periodic signal/function can be approximated by a sum (possibly infinite) sinusoidal signals. • Consider a periodic signal with period T • A periodic signal can be Real or Complex • The fundamental frequency: wo • Example:

Fourier Series • We can represent all periodic signals as harmonic series of the form – Ck are the Fourier Series Coefficients; k is real – k=0 gives the DC signal – k=+/-1 indicates the fundamental frequency or the first harmonic w 0 – |k|>=2 harmonics

Fourier Series Coefficients • Fourier Series Pair Series of complex numbers Defined over a period of x(t) • We have • For k=0, we can obtain the DC value which is the average value of x(t) over one period

Euler’s Relationship – Review Euler formulas notes

Examples • Find Fourier Series Coefficients for C 1=1/2; C-1=1/2; No DC • Find Fourier Series Coefficients for C 1=1/2 j; C-1=-1/2 j; No DC • Find Fourier Series Coefficients for notes

Different Forms of Fourier Series • Fourier Series Representation has three different forms Also: Complex Exp. Also: Harmonic Which one is this? What is the DC component? What is the expression for Fourier Series Coefficients

Examples • Find Fourier Series Coefficients for Remember:

Examples notes Find the Complex Exponential Fourier Series Coefficients textbook

Example • Find the average power of x(t) using Complex Exponential Fourier Series – assuming x(t) is periodic This is called the Parseval’s Identity

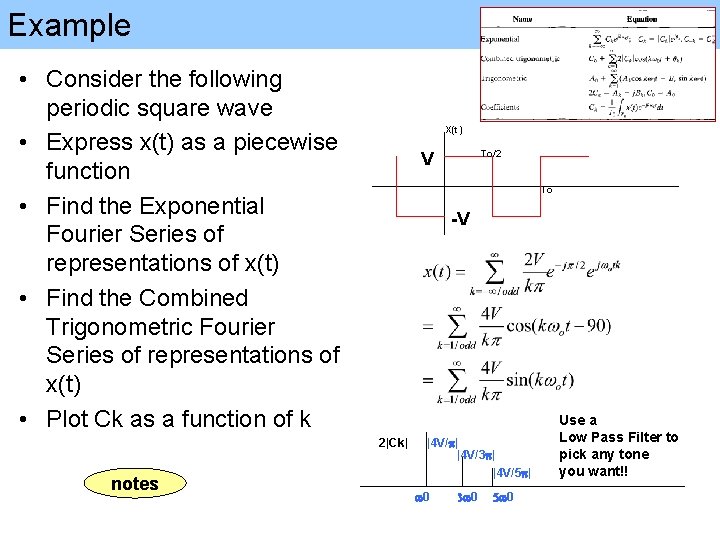
Example • Consider the following periodic square wave • Express x(t) as a piecewise function • Find the Exponential Fourier Series of representations of x(t) • Find the Combined Trigonometric Fourier Series of representations of x(t) • Plot Ck as a function of k X(t) To -V 2|Ck| notes To/2 V |4 V/p| |4 V/3 p| |4 V/5 p| w 0 3 w 0 5 w 0 Use a Low Pass Filter to pick any tone you want!!

Practical Application • Using a XTL oscillator which produces positive 1 Vp-p how can you generate a sinusoidal waveforms with different frequencies?

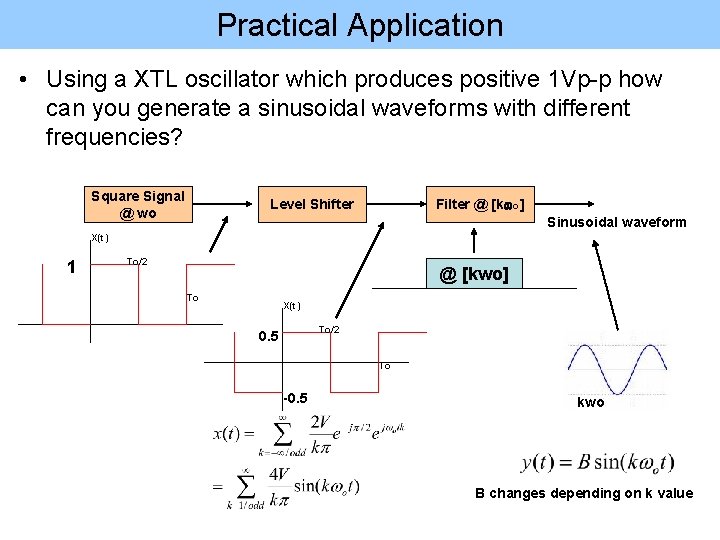
Practical Application • Using a XTL oscillator which produces positive 1 Vp-p how can you generate a sinusoidal waveforms with different frequencies? Square Signal @ wo Level Shifter Filter @ [kwo] Sinusoidal waveform X(t) 1 To/2 @ [kwo] To X(t) To/2 0. 5 To -0. 5 kwo B changes depending on k value

Demo Ck corresponds to frequency components In the signal.

Example • Given the following periodic square wave, find the Fourier Series representations and plot Ck as a function of k. 1 Note: sinc (infinity) 1 & Max value of sinc(x) 1/x Sinc Function Only a function of freq. Note: First zero occurs at Sinc (+/-pi)

Use the Fourier Series Table (Table 4. 3) • Consider the following periodic square wave • Find the Exponential Fourier Series of representations of x(t) X(t) To/2 V To -V • X 0 V 2|Ck| |4 V/p| |4 V/3 p| |4 V/5 p| w 0 3 w 0 5 w 0

Fourier Series - Applet http: //www. falstad. com/fourier/

Using Fourier Series Table • Given the following periodic square wave, find the Fourier Series representations and plot Ck as a function of k. (Rectangular wave) X 0 1 C 0=T/To T/2=T 1 T=2 T 1 Ck=T/T 0 sinc (Tkw 0/2) Same as before Note: sinc (infinity) 1 & Max value of sinc(x) 1/x

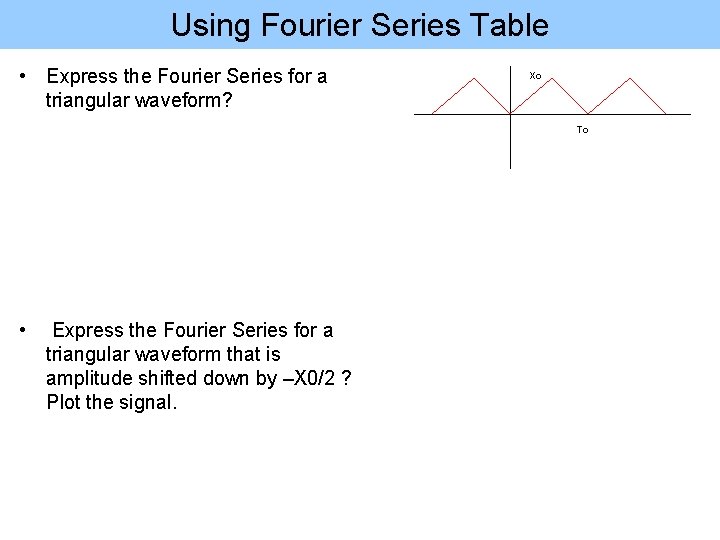
Using Fourier Series Table • Express the Fourier Series for a triangular waveform? Xo To • Express the Fourier Series for a triangular waveform that is amplitude shifted down by –X 0/2 ? Plot the signal.

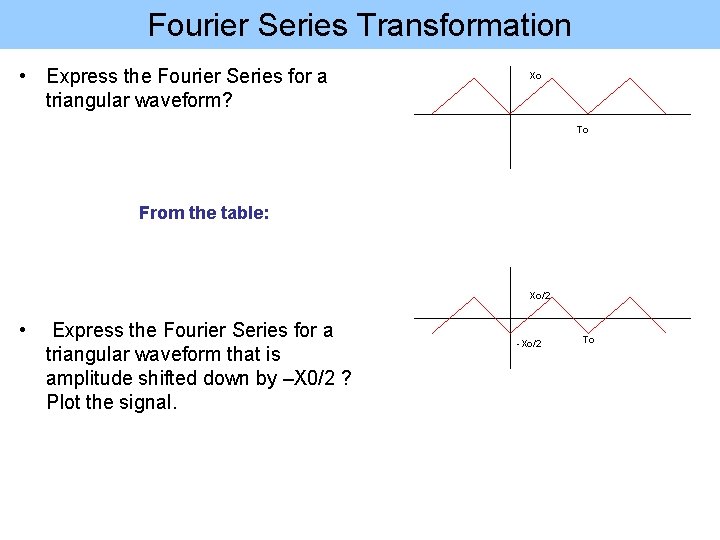
Fourier Series Transformation • Express the Fourier Series for a triangular waveform? Xo To From the table: Xo/2 • Express the Fourier Series for a triangular waveform that is amplitude shifted down by –X 0/2 ? Plot the signal. -Xo/2 To

Fourier Series Transformation • Express the Fourier Series for a triangular waveform? Xo To From the table: Xo/2 • Express the Fourier Series for a triangular waveform that is amplitude shifted down by –X 0/2 ? Plot the signal. Only DC value changed! -Xo/2 To

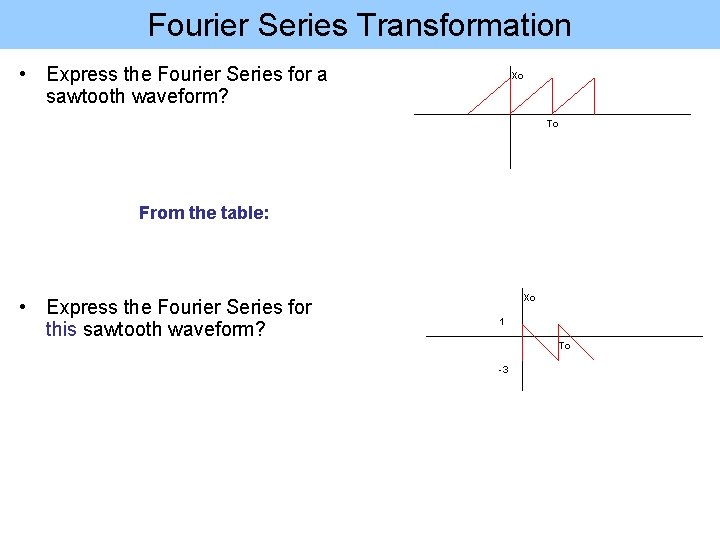
Fourier Series Transformation • Express the Fourier Series for a sawtooth waveform? Xo To From the table: • Express the Fourier Series for this sawtooth waveform? Xo 1 To -3

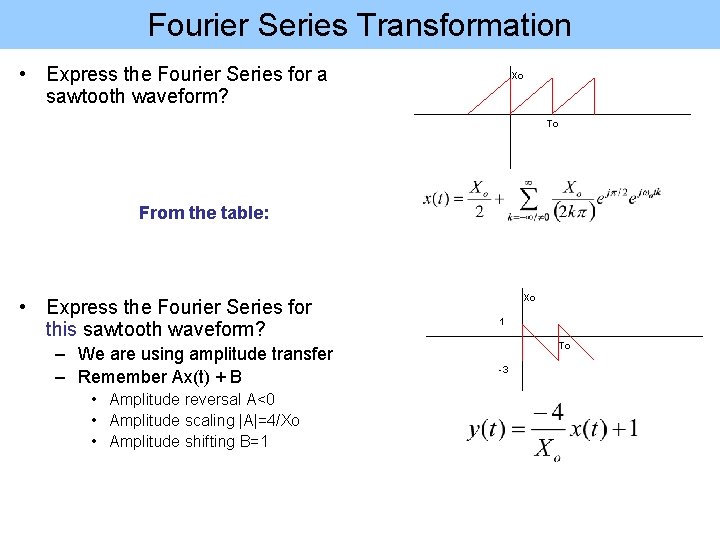
Fourier Series Transformation • Express the Fourier Series for a sawtooth waveform? Xo To From the table: • Express the Fourier Series for this sawtooth waveform? – We are using amplitude transfer – Remember Ax(t) + B • Amplitude reversal A<0 • Amplitude scaling |A|=4/Xo • Amplitude shifting B=1 Xo 1 To -3

Example

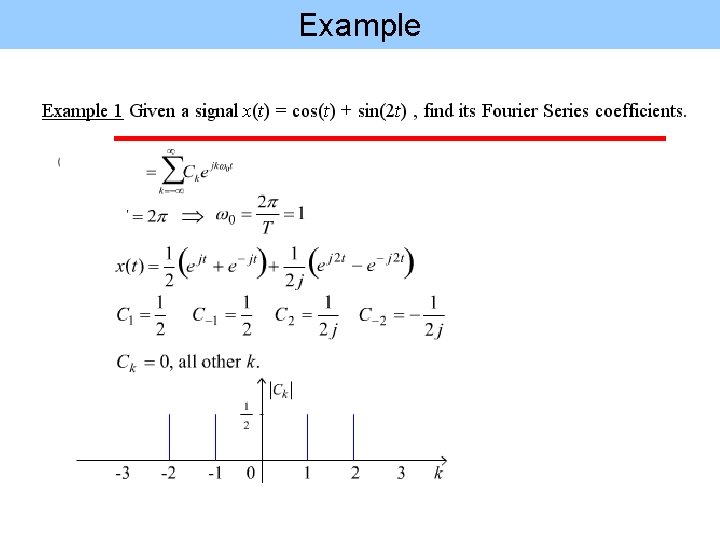
Example

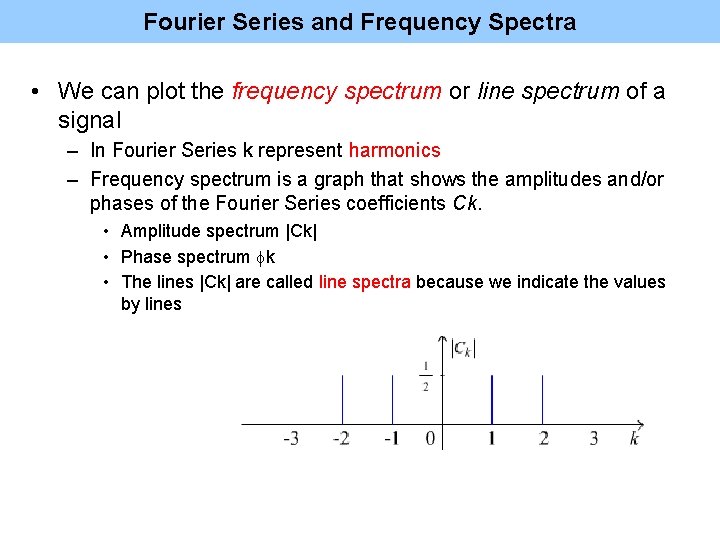
Fourier Series and Frequency Spectra • We can plot the frequency spectrum or line spectrum of a signal – In Fourier Series k represent harmonics – Frequency spectrum is a graph that shows the amplitudes and/or phases of the Fourier Series coefficients Ck. • Amplitude spectrum |Ck| • Phase spectrum fk • The lines |Ck| are called line spectra because we indicate the values by lines

Schaum’s Outline Problems • Schaum’s Outline Chapter 5 Problems: – 4, 5 6, 7, 8, 9, 10 • Do all the problems in chapter 4 of the textbook • Skip the following Sections in the text: – 4. 5 • Read the following Sections in the textbook on your own – 4. 4