Chapter 4 Force System Resultants Engineering Mechanics Statics

Chapter 4: Force System Resultants Engineering Mechanics: Statics Ahmad Faizal bin Salleh 2014/2015

Chapter Objectives • Concept of moment of a force in two and three dimensions • Method for finding the moment of a force about a specified axis. • Define the moment of a couple. • Determine the resultants of nonconcurrent force systems • Reduce a simple distributed loading to a resultant force having a specified location

Chapter Outline 1. Moment of a Force – Scalar Formation 2. Cross Product 3. Moment of Force – Vector Formulation 4. Principle of Moments 5. Moment of a Force about a Specified Axis 6. Moment of a Couple 7. Simplification of a Force and Couple System

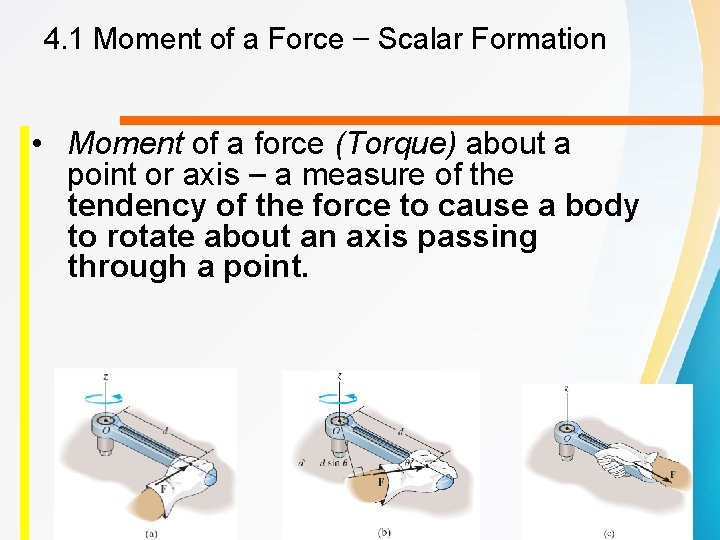
4. 1 Moment of a Force – Scalar Formation • Moment of a force (Torque) about a point or axis – a measure of the tendency of the force to cause a body to rotate about an axis passing through a point.

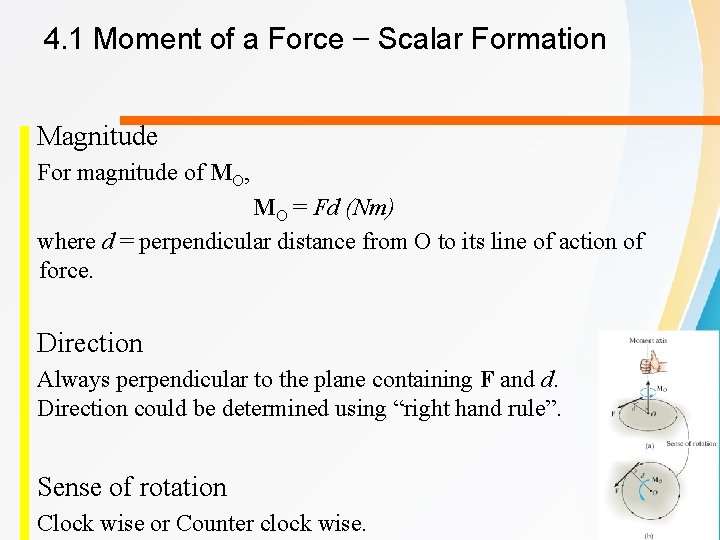
4. 1 Moment of a Force – Scalar Formation Magnitude For magnitude of MO, MO = Fd (Nm) where d = perpendicular distance from O to its line of action of force. Direction Always perpendicular to the plane containing F and d. Direction could be determined using “right hand rule”. Sense of rotation Clock wise or Counter clock wise.

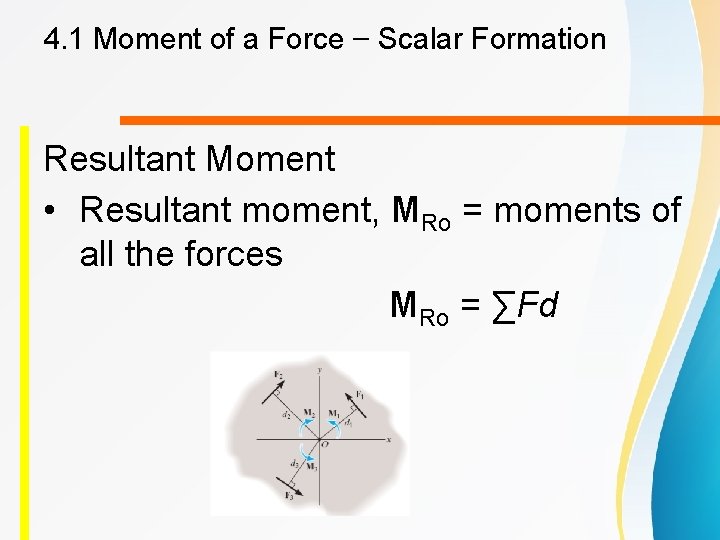
4. 1 Moment of a Force – Scalar Formation Resultant Moment • Resultant moment, MRo = moments of all the forces MRo = ∑Fd

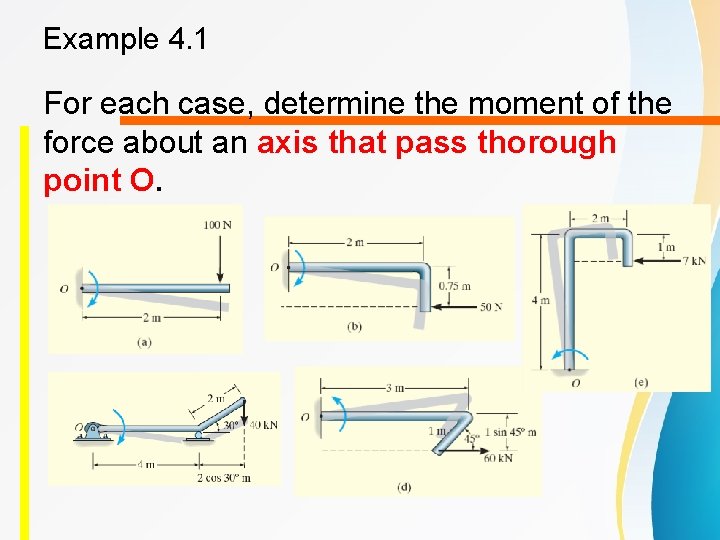
Example 4. 1 For each case, determine the moment of the force about an axis that pass thorough point O.

Solution Line of action is extended as a dashed line to establish moment arm d. Tendency to rotate is indicated and the orbit is shown as a colored curl.

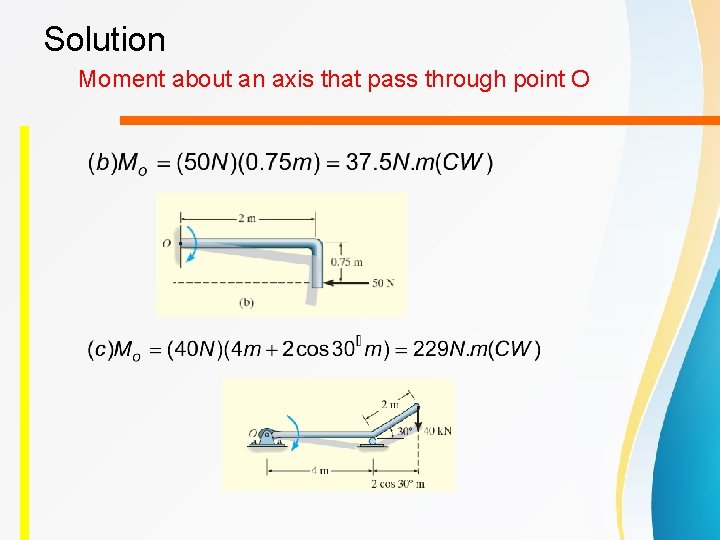
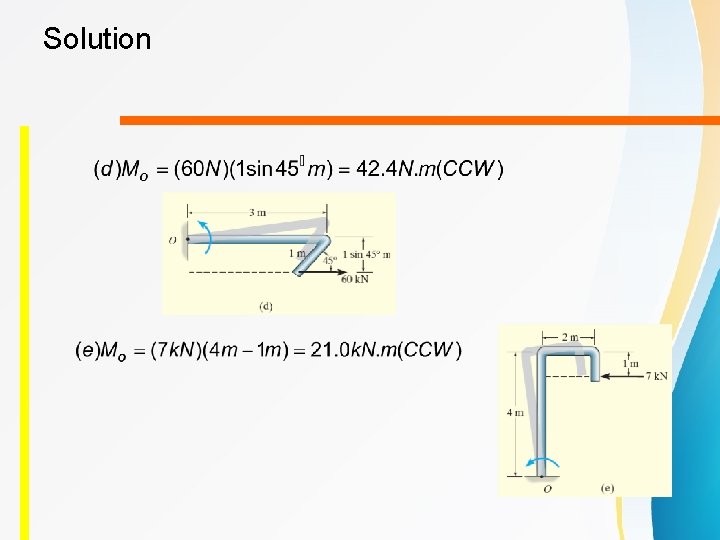
Solution Moment about an axis that pass through point O

Solution

4. 4 Principles of Moments (This is good for 2 D vector analysis, that is why I bring section 4. 4 after 4. 1) • Also known as Varignon’s Theorem “Moment of a force about a point is equal to the sum of the moments of the forces’ components about the point” • Since F = F 1 + F 2, MO = r X F = r X (F 1 + F 2) = r X F 1 + r X F 2

Example 4. 4 - 1 Without utilizing Varignon's theorem, the moment of the force about an axis perpendicular to a plane containing force, F and distance, d is, Assume that CCW is +ve,

Example 4. 4 - 1 Utilizing Varignon's theorem, assume that CCW is positive. MO = (-1)* 5 k. N*cos 45°* 3 sin 30°+ (-1)*5 k. N*sin 45°* 3 cos 30°= ? k. Nm Thus, Since the force tends to rotate or orbit clockwise about point O, the moment is directed into the page.

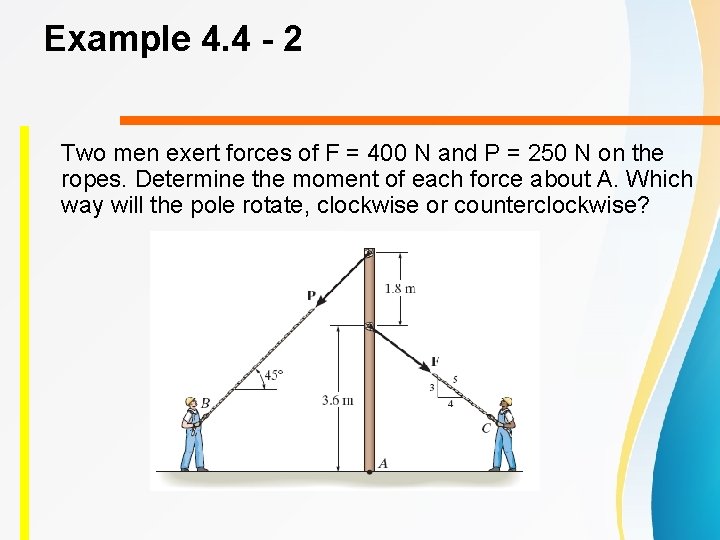
Example 4. 4 - 2 Two men exert forces of F = 400 N and P = 250 N on the ropes. Determine the moment of each force about A. Which way will the pole rotate, clockwise or counterclockwise?

Example 4. 4 - 2

4. 2 Cross Product Useful for calculating 3 D moment’s vector • Cross product of two vectors A and B yields C, which is written as C = A X B Magnitude • Magnitude of C is the product of the magnitudes of A and B • For angle θ, 0° ≤ θ ≤ 180° C = AB sinθ

4. 2 Cross Product Direction • Vector C has a direction that is perpendicular to the plane containing A and B such that C is specified by the right hand rule • Expressing vector C when magnitude and direction are known C = A X B = (AB sinθ)u. C

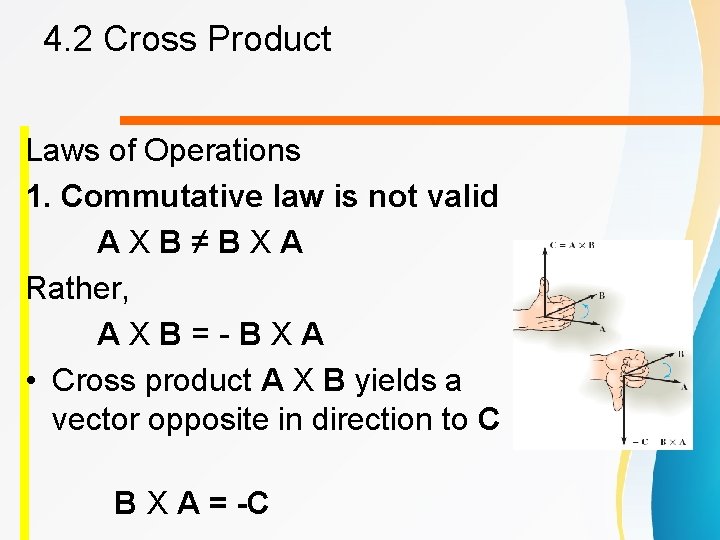
4. 2 Cross Product Laws of Operations 1. Commutative law is not valid A X B ≠ B X A Rather, A X B = - B X A • Cross product A X B yields a vector opposite in direction to C B X A = -C

4. 2 Cross Product Laws of Operations 2. Multiplication by a Scalar a( A X B ) = (a. A) X B = A X (a. B) = ( A X B )a 3. Distributive Law A X ( B + D ) = ( A X B ) + ( A X D ) • Proper order of the cross product must be maintained since they are not

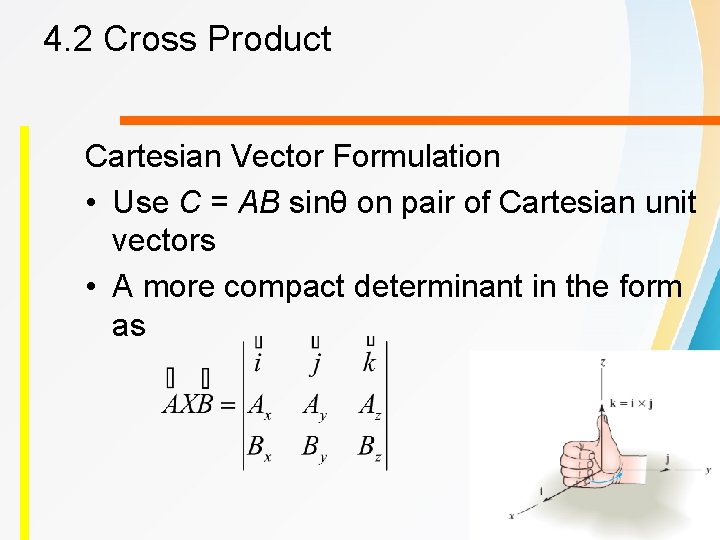
4. 2 Cross Product Cartesian Vector Formulation • Use C = AB sinθ on pair of Cartesian unit vectors • A more compact determinant in the form as

4. 3 Moment of Force - Vector Formulation Moment of force F about point O can be expressed using cross product MO = r X F Moment vector, Mo pass through O and perpendicular to the plane containing r and F. Position vector, r directed from O to any point on the line of action of F.

4. 3 Moment of Force - Vector Formulation Direction • Direction and sense of MO are determined by right -hand rule *Note: - “curl” of the fingers indicates the sense of rotation (CW or CCW) - Maintain proper order of r and F since cross product is not commutative

4. 3 Moment of Force - Vector Formulation Cartesian Vector Formulation • For force expressed in Cartesian form, • With the determinant expended, MO = (ry. Fz – rz. Fy)i – (rx. Fz - rz. Fx)j + (rx. Fy – y. Fx)k

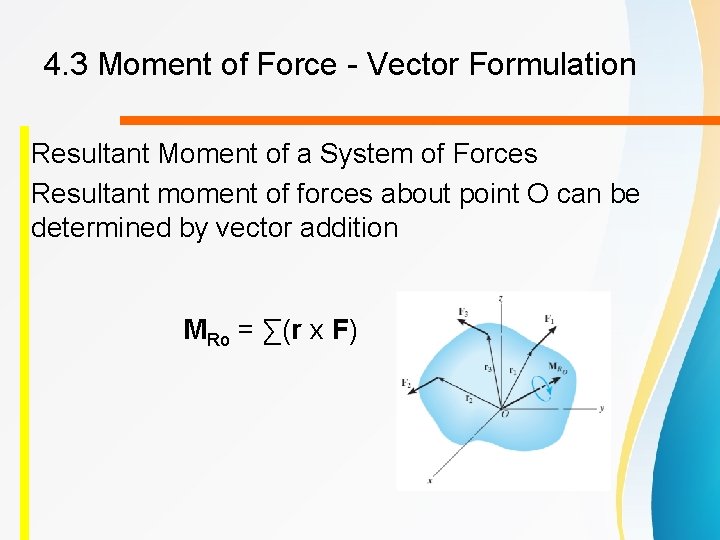
4. 3 Moment of Force - Vector Formulation Resultant Moment of a System of Forces Resultant moment of forces about point O can be determined by vector addition MRo = ∑(r x F)

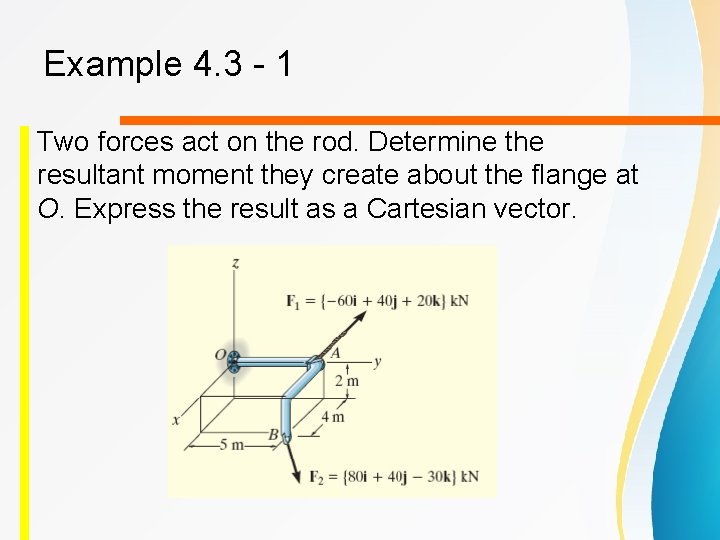
Example 4. 3 - 1 Two forces act on the rod. Determine the resultant moment they create about the flange at O. Express the result as a Cartesian vector.

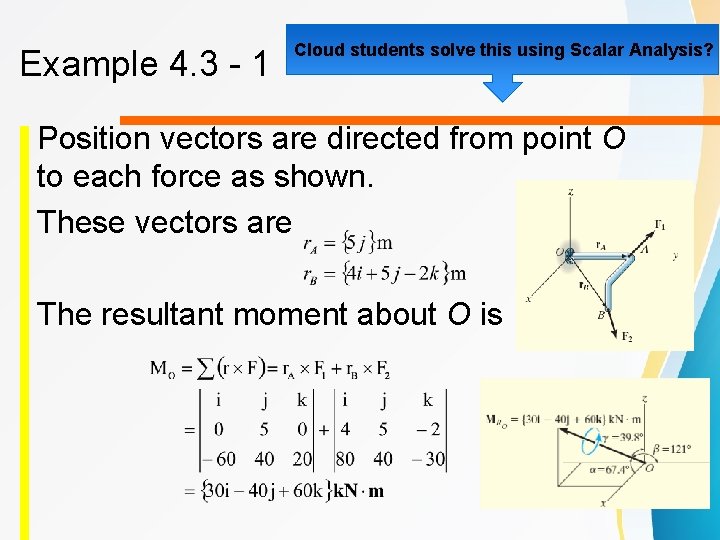
Example 4. 3 - 1 Cloud students solve this using Scalar Analysis? Position vectors are directed from point O to each force as shown. These vectors are The resultant moment about O is

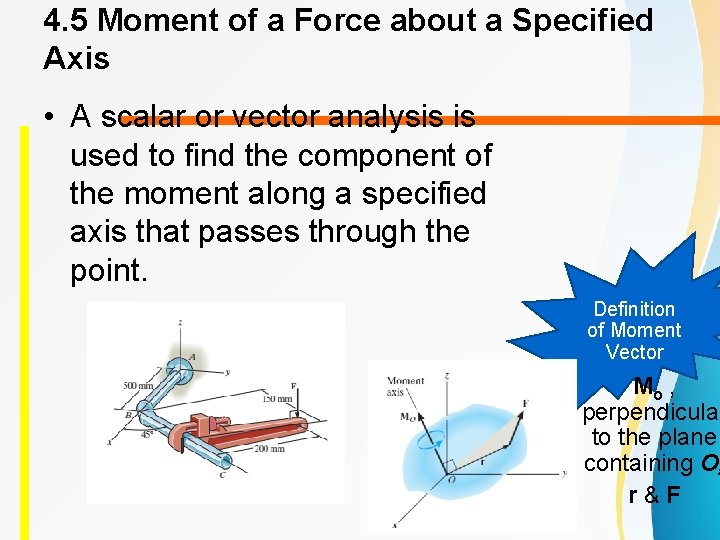
4. 5 Moment of a Force about a Specified Axis • A scalar or vector analysis is used to find the component of the moment along a specified axis that passes through the point. Definition of Moment Vector Mo , perpendicular to the plane containing O, r & F

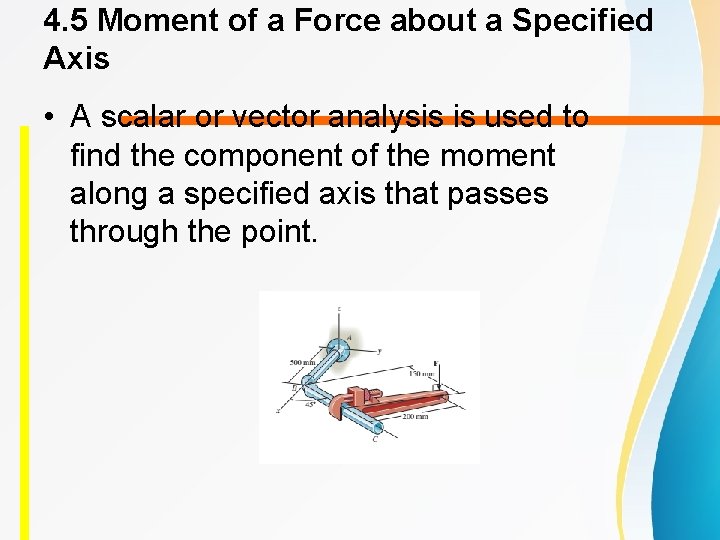
4. 5 Moment of a Force about a Specified Axis • A scalar or vector analysis is used to find the component of the moment along a specified axis that passes through the point.

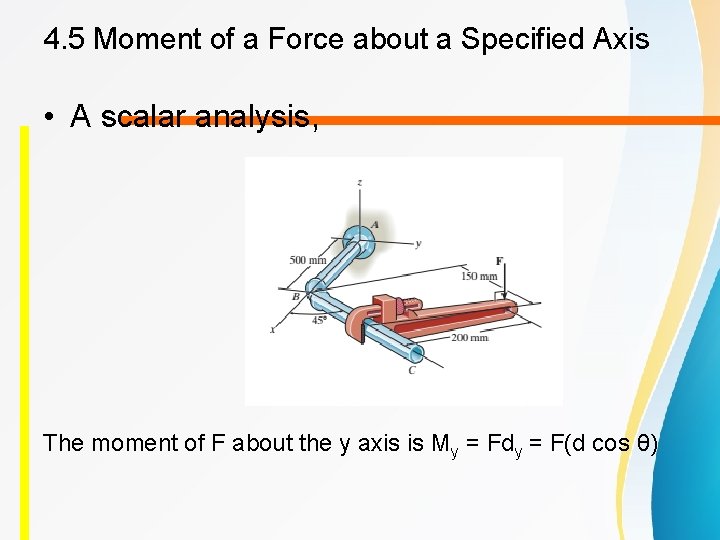
4. 5 Moment of a Force about a Specified Axis • A scalar analysis, The moment of F about the y axis is My = Fdy = F(d cos θ)

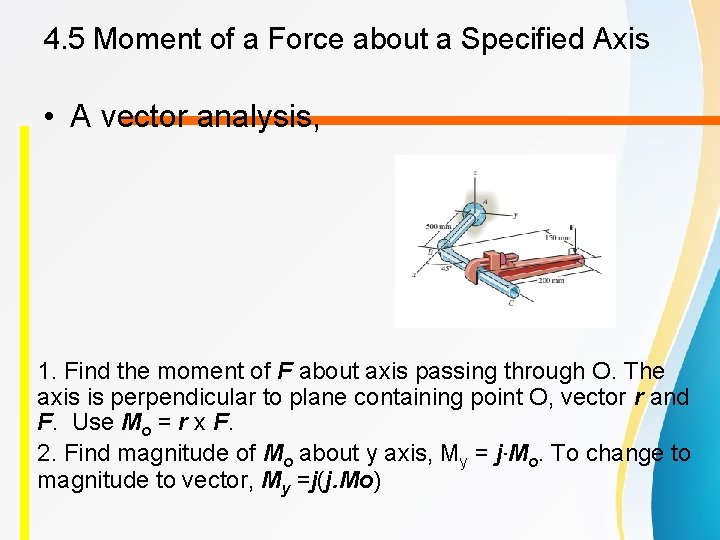
4. 5 Moment of a Force about a Specified Axis • A vector analysis, 1. Find the moment of F about axis passing through O. The axis is perpendicular to plane containing point O, vector r and F. Use Mo = r x F. 2. Find magnitude of Mo about y axis, My = j·Mo. To change to magnitude to vector, My =j(j. Mo)

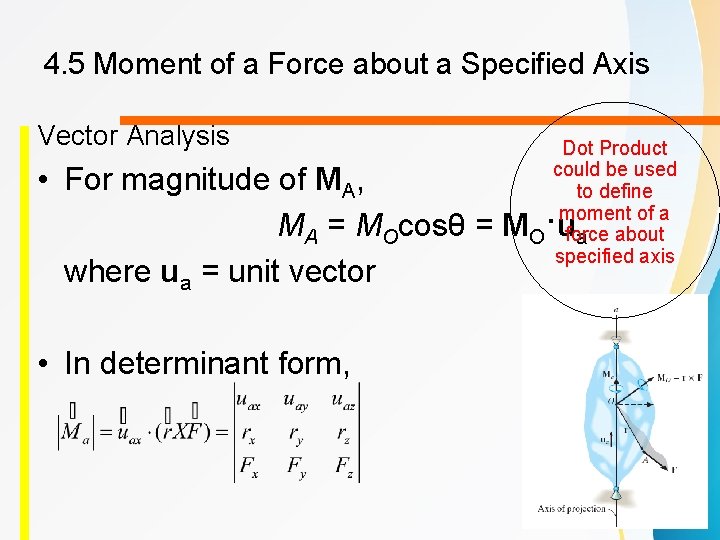
4. 5 Moment of a Force about a Specified Axis Vector Analysis Dot Product could be used to define moment of a O force about a specified axis • For magnitude of MA, MA = MOcosθ = M ·u where ua = unit vector • In determinant form,

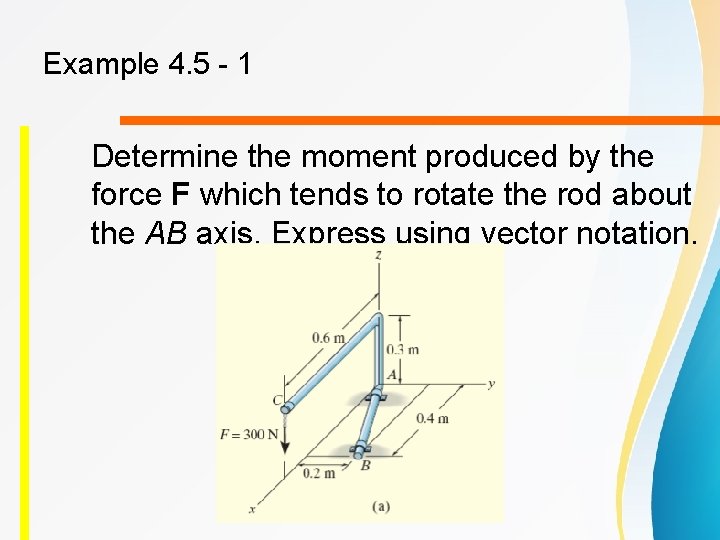
Example 4. 5 - 1 Determine the moment produced by the force F which tends to rotate the rod about the AB axis. Express using vector notation.

Example 4. 5 - 1 Unit vector defines the direction of the AB axis of the rod, where For simplicity, choose r. D The force is

EXAMPLE OF HUMAN A case where your try to rotate something on with the centre of your hand. The moment created about an axis and this axis may not be aligned with the axis of your elbow. Thus, you need to calculate the moment created about your elbow's axis.

WED, 20 Sept 2017 Copyright © 2010 Pearson Education South Asia Pte Ltd

WHAT WE HAVE LEARNT SO FAR? 1. Determining moment of a force (torque) in 2 D Moment arm x Force. 2. Principle of moments - also known as Varignon's theorem. 3. Determining torque in 3 D using Cross Product. 4. Determining torque about a specified axis.

4. 6 Moment of a Couple • Couple – two parallel forces, separated by perpendicular distance d (non-collinear) – same magnitude but opposite direction • Resultant force = 0 • Tendency to rotate in specified direction

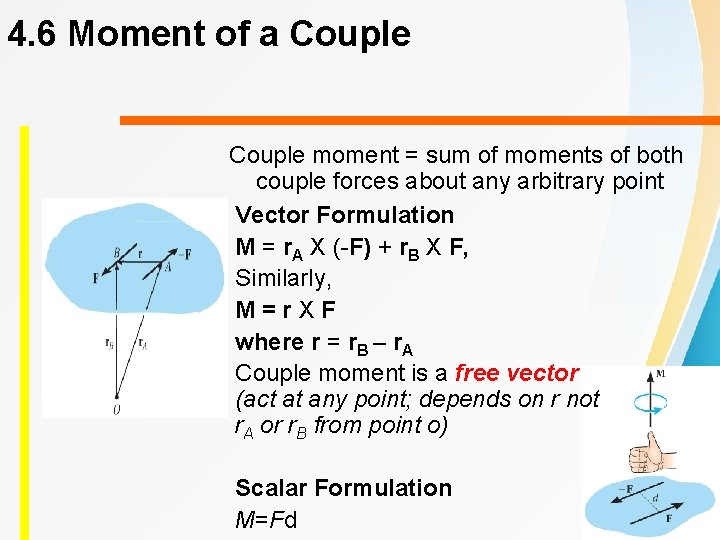
4. 6 Moment of a Couple moment = sum of moments of both couple forces about any arbitrary point Vector Formulation M = r. A X (-F) + r. B X F, Similarly, M = r X F where r = r. B – r. A Couple moment is a free vector (act at any point; depends on r not r. A or r. B from point o) Scalar Formulation M=Fd

4. 6 Moment of a Couple Unlike Moment of Force (Torque) Resultant Couple Moment • Couple moments are free vectors and may be applied to any point P and added vectorially. • For resultant moment of two couples at point P, MR = M 1 + M 2 • For more than 2 moments, MR = ∑(r X F)

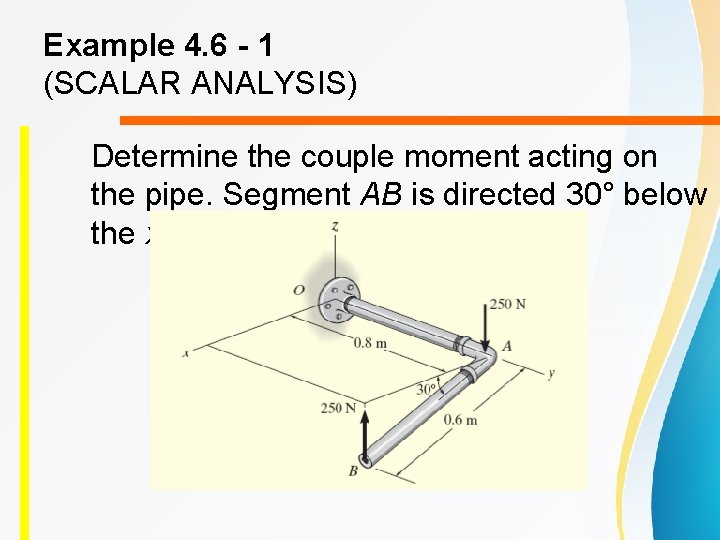
Example 4. 6 - 1 (SCALAR ANALYSIS) Determine the couple moment acting on the pipe. Segment AB is directed 30° below the x–y plane.

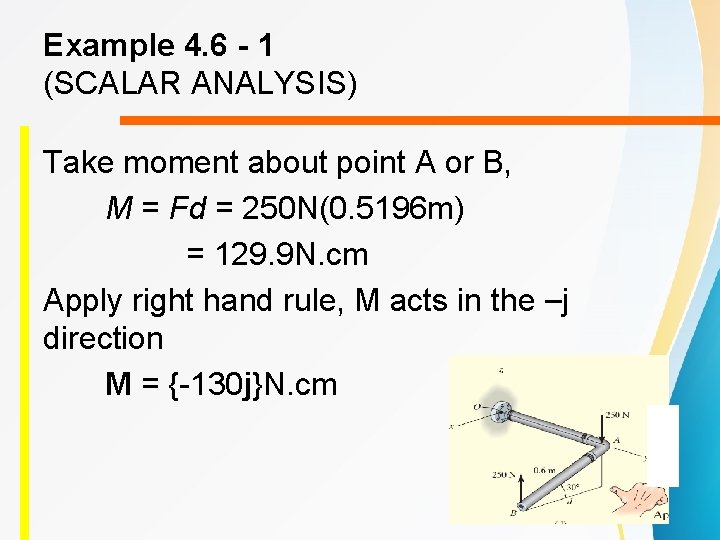
Example 4. 6 - 1 (SCALAR ANALYSIS) Take moment about point A or B, M = Fd = 250 N(0. 5196 m) = 129. 9 N. cm Apply right hand rule, M acts in the –j direction M = {-130 j}N. cm

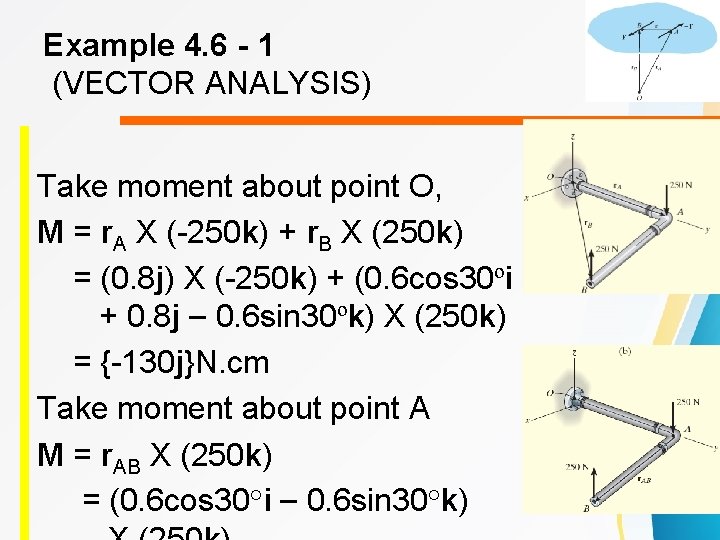
Example 4. 6 - 1 (VECTOR ANALYSIS) Take moment about point O, M = r. A X (-250 k) + r. B X (250 k) = (0. 8 j) X (-250 k) + (0. 6 cos 30ºi + 0. 8 j – 0. 6 sin 30ºk) X (250 k) = {-130 j}N. cm Take moment about point A M = r. AB X (250 k) = (0. 6 cos 30°i – 0. 6 sin 30°k)

4. 6 Moment of force and moment of a couple 1. Moment of force is the measure of turning effect of a force about an axis passing through a point. 2. A couple consists of two equal and opposite forces acting with two different but parallel lines of action. Each force has its own moment. 3. Moment of a force is dependent on the distance from the pivot and the magnitude of the force. 4. Moment of a couple is the net effect of the two moments of the forces and independent of the location of the point considered. It is constant throughout the plane.

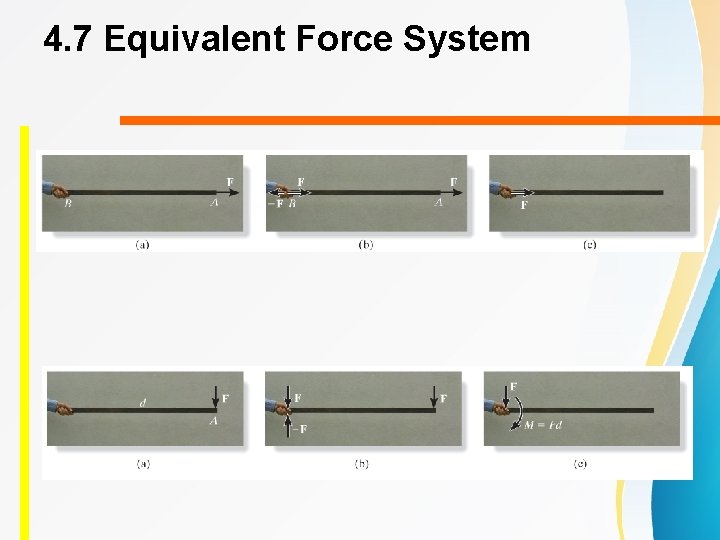
4. 7 Equivalent Force System

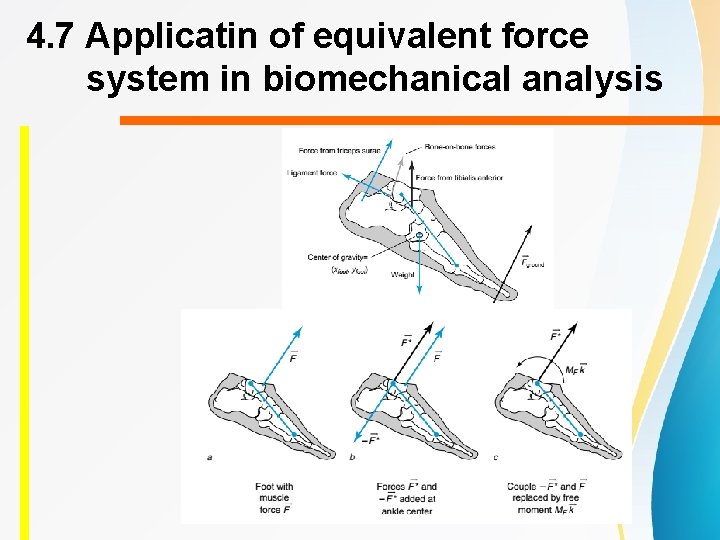
4. 7 Applicatin of equivalent force system in biomechanical analysis

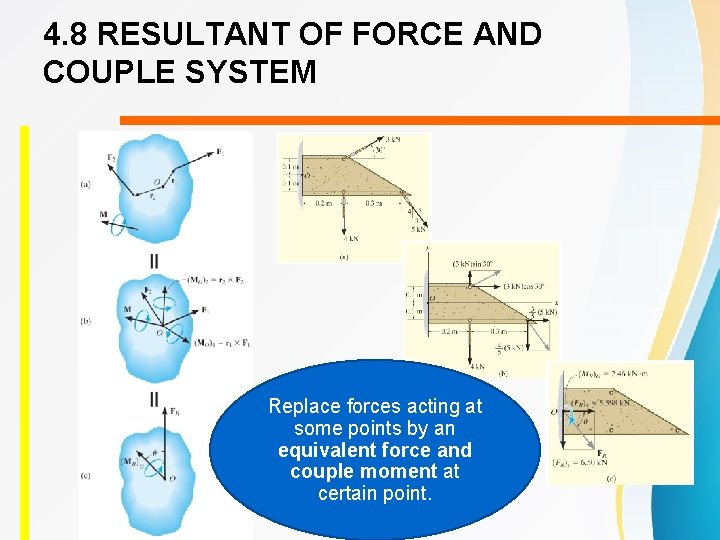
4. 8 RESULTANT OF FORCE AND COUPLE SYSTEM Replace forces acting at some points by an equivalent force and couple moment at certain point.

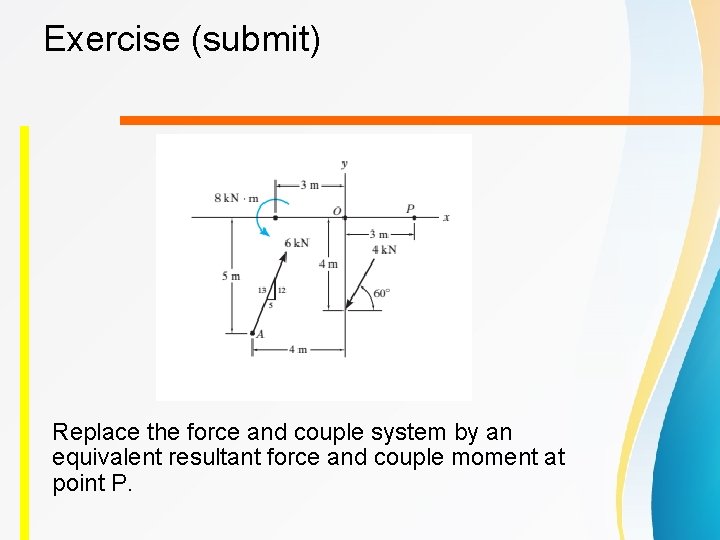
Exercise (submit) Replace the force and couple system by an equivalent resultant force and couple moment at point P.

4. 9 SIMPLIFICATION TO A SINGLE RESULTANT FORCE: COPLANAR FORCE SYSTEM In coplanar but non concurrent force system, once you have simplified a system of forces into a resultant force and couple, then, you could simplified it further to a single resultant force. This condition MUST be satisfied **Line of action of (MR)O and FR are perpedicular**

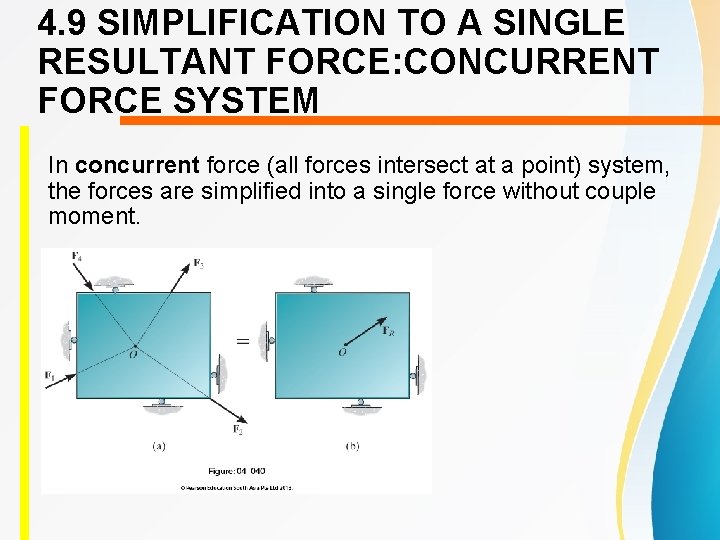
4. 9 SIMPLIFICATION TO A SINGLE RESULTANT FORCE: CONCURRENT FORCE SYSTEM In concurrent force (all forces intersect at a point) system, the forces are simplified into a single force without couple moment.

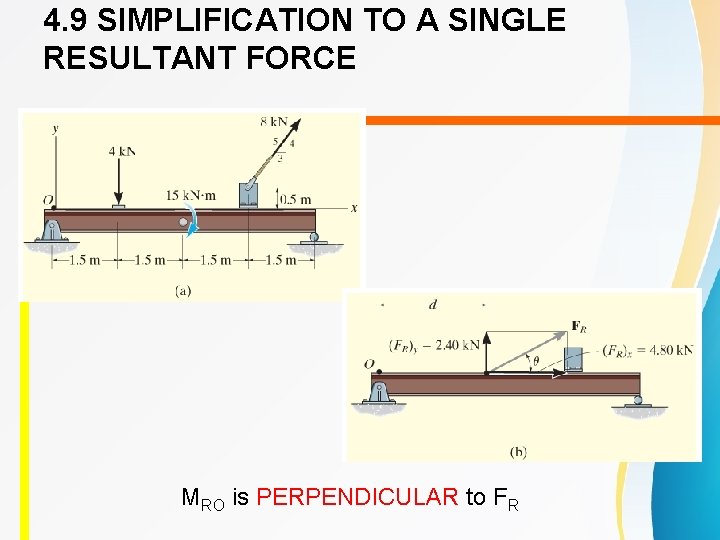
4. 9 SIMPLIFICATION TO A SINGLE RESULTANT FORCE MRO is PERPENDICULAR to FR

IMPORTANT POINTS 1. System of forces and couple moments could be reduce to a simpler form by replacing it with equivalent system. 2. If it is a coplanar force system, reduce it to a force and a couple moment. Then, you could reduce it further to a single force provided the line of action of the couple moment and force is perpendicular.

4. 10 Reduction of a Simple Distributed Loading • Large surface area of a body may be subjected to distributed loadings • Loadings on the surface is defined as pressure • Pressure is measured in Pascal (Pa): 1 Pa = 1 N/m 2

4. 10 Reduction of a Simple Distributed Loading P(x) has a unit of N/m 2, contain only variable x and thus can represent coplanar distributed load. To represent as coplanar distributed load, we multiply w(x) N/m = P N/m 2 x b m

4. 10 Reduction of a Simple Distributed Loading What we are going to do next is to replace the coplanar force system with a single resultant force, FR.

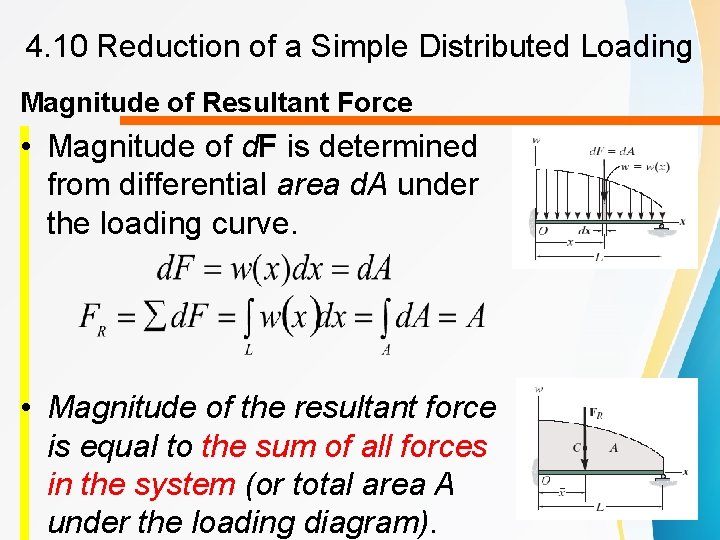
4. 10 Reduction of a Simple Distributed Loading Magnitude of Resultant Force • Magnitude of d. F is determined from differential area d. A under the loading curve. • Magnitude of the resultant force is equal to the sum of all forces in the system (or total area A under the loading diagram).

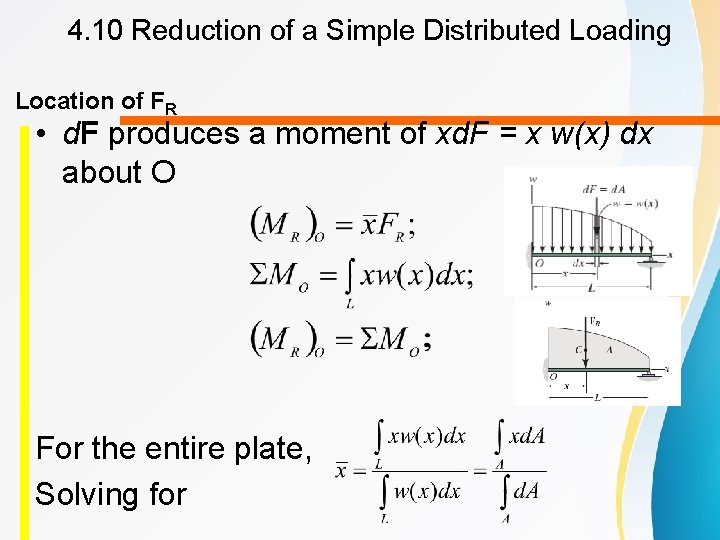
4. 10 Reduction of a Simple Distributed Loading Location of Resultant Force Location of FR • Moment created by FR about an axis passing through O is (MR)o. Moment created by the parallel force distribution is ∑MO. This condition is satisfied by both moments, • d. F produces a moment of xd. F = x w(x) dx about O.

4. 10 Reduction of a Simple Distributed Loading Location of FR • d. F produces a moment of xd. F = x w(x) dx about O For the entire plate, Solving for

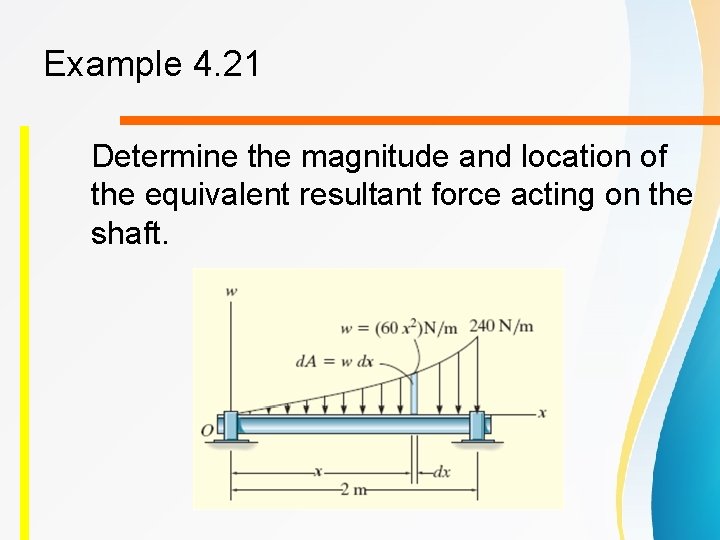
Example 4. 21 Determine the magnitude and location of the equivalent resultant force acting on the shaft.

Solution For the colored differential area element, For resultant force

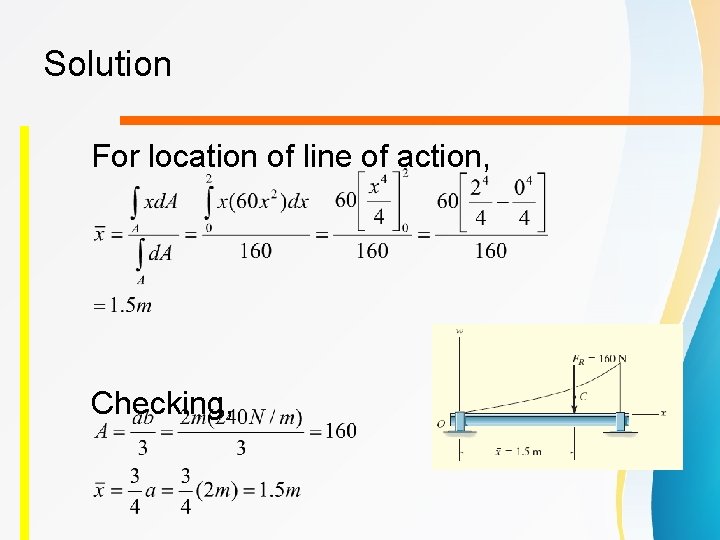
Solution For location of line of action, Checking,

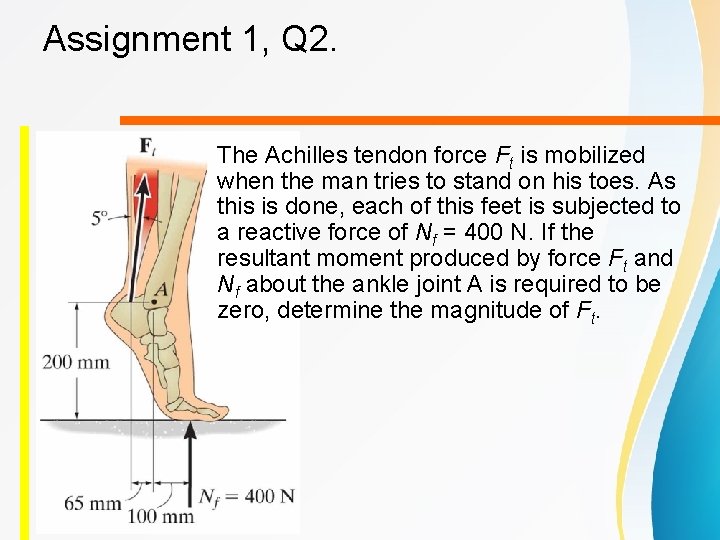
Assignment 1, Q 2. The Achilles tendon force Ft is mobilized when the man tries to stand on his toes. As this is done, each of this feet is subjected to a reactive force of Nf = 400 N. If the resultant moment produced by force Ft and Nf about the ankle joint A is required to be zero, determine the magnitude of Ft.