CHAPTER 4 Electron Configurations current model of the

CHAPTER 4 Electron Configurations (current model of the atom) The Schrodinger Model 1. only certain places where electrons can be _____ Bohr The consequence of… 2. electrons behave as waves and as particles de. Broglie, Davisson and Germer __________ 3. can’t know precisely where an electron is ________ Heisenberg is that, when we describe / define atomic structure (specifically where e- can be) rg e b n of finding an ee s we can only speak of the ______ probability i He at a particular point r h Bo in a particular spatial region around the nucleus orbitals… 3 D wave shapes

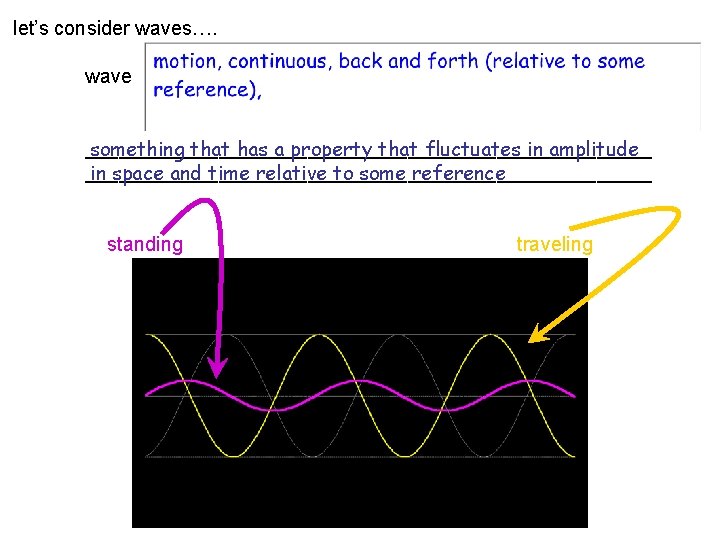
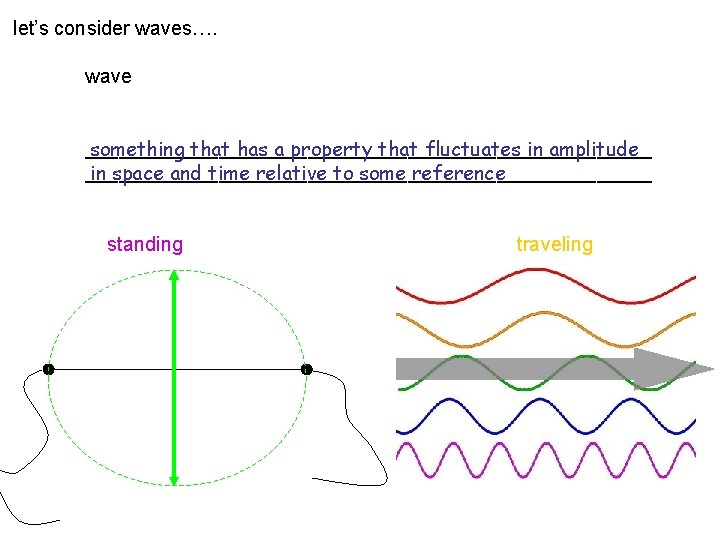
let’s consider waves…. wave __________________________ something that has a property that fluctuates in amplitude __________________________ in space and time relative to some reference standing traveling

let’s consider waves…. wave __________________________ something that has a property that fluctuates in amplitude __________________________ in space and time relative to some reference standing traveling

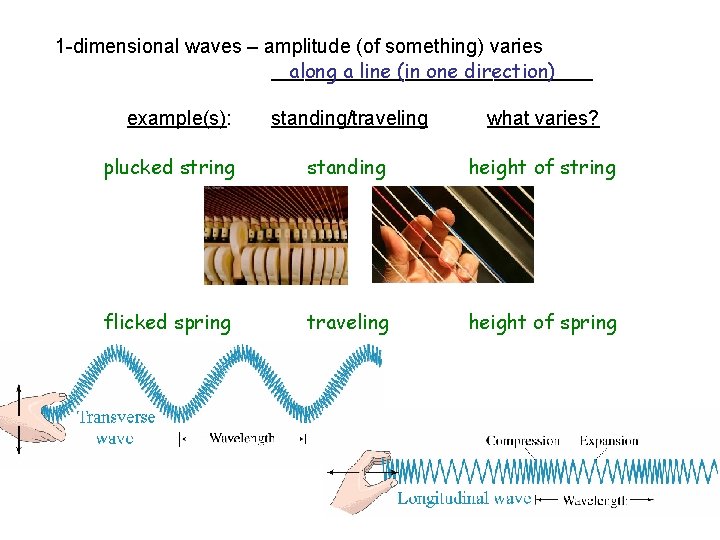
1 -dimensional waves – amplitude (of something) varies _______________ along a line (in one direction) example(s): plucked string standing/traveling what varies? standing height of string

1 -dimensional waves – amplitude (of something) varies _______________ along a line (in one direction) example(s): standing/traveling what varies? plucked string standing height of string flicked spring traveling height of spring

2 -dimensional waves – amplitude (of something) varies _______________ along a plane (in two directions) example(s): standing/traveling what varies? water wave w/ dropped pebble traveling height of water

2 -dimensional waves – amplitude (of something) varies _______________ along a plane (in two directions) example(s): standing/traveling what varies? water wave w/ dropped pebble traveling height of water struck drum standing height of drum skin

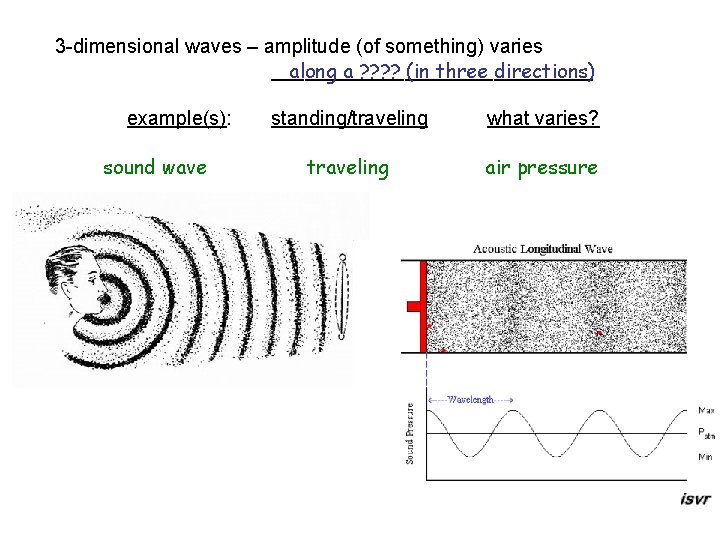
3 -dimensional waves – amplitude (of something) varies _______________ along a ? ? (in three directions) example(s): sound wave standing/traveling what varies? traveling air pressure

3 -dimensional waves – amplitude (of something) varies _______________ along a ? ? (in three directions) example(s): standing/traveling what varies? sound wave traveling air pressure earthquake (seismic wave) traveling compression of land seismic wave

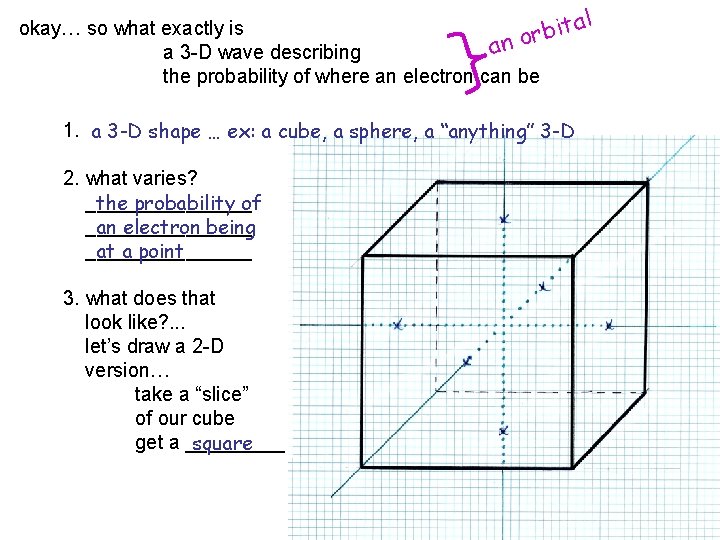
al t okay… so what exactly is i b or n a a 3 -D wave describing the probability of where an electron can be 1. a 3 -D shape … ex: a cube, a sphere, a “anything” 3 -D 2. what varies? ________ the probability of ________ an electron being ________ at a point 3. what does that look like? . . . let’s draw a 2 -D version… take a “slice” of our cube get a _____ square

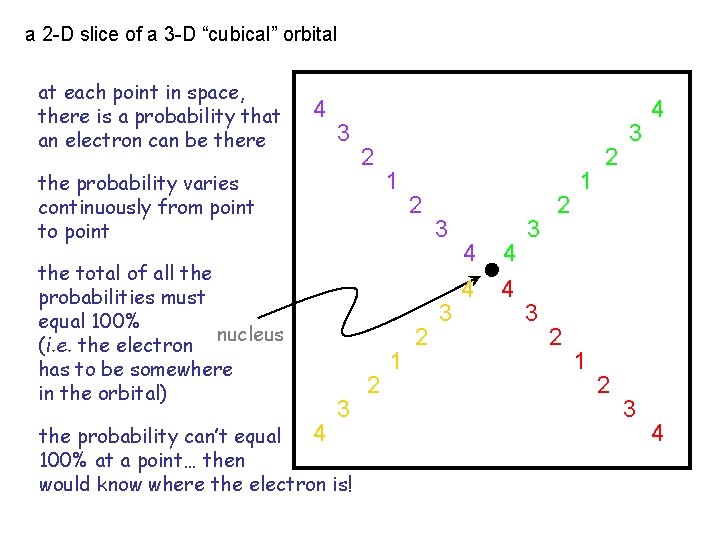
a 2 -D slice of a 3 -D “cubical” orbital at each point in space, there is a probability that an electron can be there 4 3 the probability varies continuously from point to point the total of all the probabilities must equal 100% nucleus (i. e. the electron has to be somewhere in the orbital) 3 4 the probability can’t equal 100% at a point… then would know where the electron is! 2 2 1 1 2 2 3 3 4 4 3 3 2 2 1 1 2 2 3 3 4 4

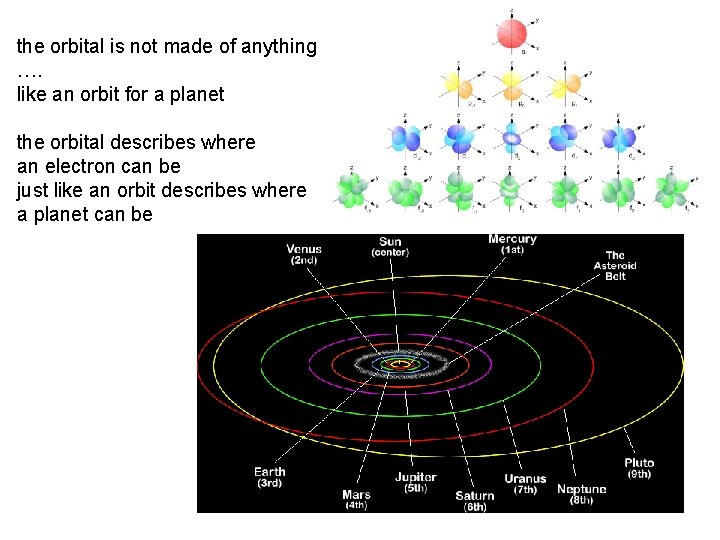
the orbital is not made of anything …. like an orbit for a planet the orbital describes where an electron can be just like an orbit describes where a planet can be

electron orbitals only certain shapes can exist Bohr’s orbits ed z i nt qua 1, 2, 3, 4, …. n = _____________ atomic number (# protons) Z = _____________ Schrodinger (!!!) y nl o … ain t r ce s ce a l p

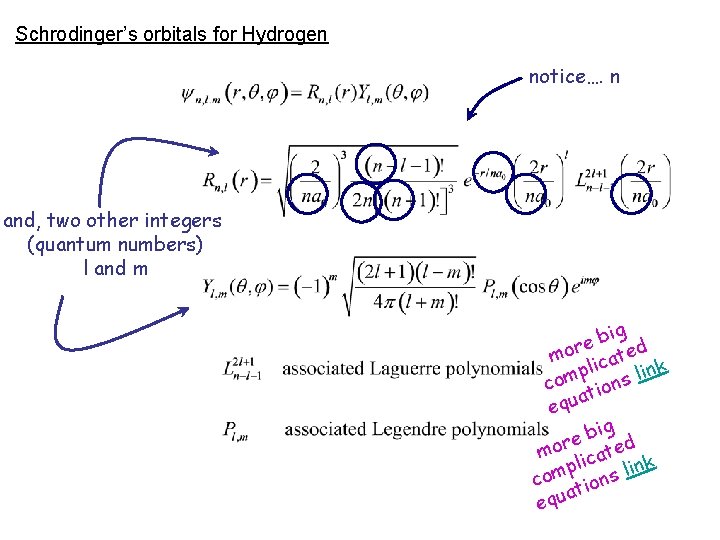
Schrodinger’s orbitals for Hydrogen notice…. n and, two other integers (quantum numbers) l and m ig b e mor icated pl s link m o c ion t a equ

electron orbitals only certain shapes can exist Bohr’s orbits ed z i nt y nl o … ain t r ce s ce a l p qua n = 1, 2, 3, 4, …. atomic number (# protons) Z = _____________ Schrodinger (slightly more complex!!!) just as n defines the size of the orbit in Bohr’s model the three quantum numbers ________ n, l, and m in part define ______________ the size and shape of the orbitals we’ll only consider the value of n r h o B 1, 2, 3, 4, 5, …. or n = _____________ f e lik as n increases t s u j ______________ the size of the orbital increases

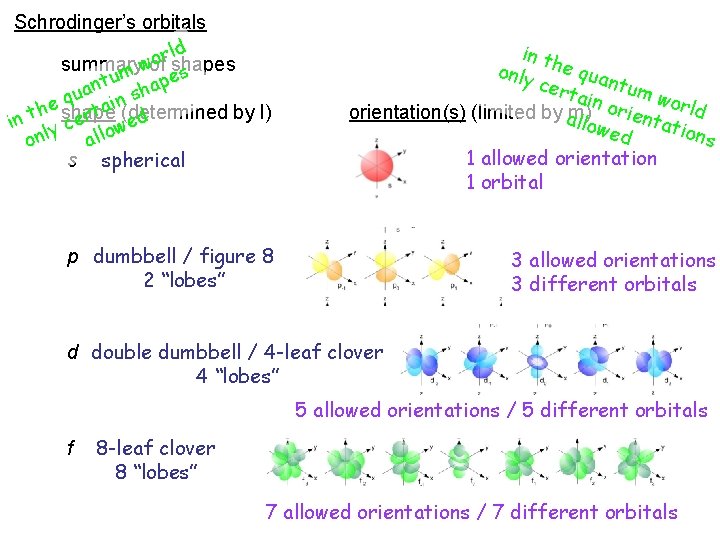
Schrodinger’s orbitals summary of shapes n, l, and m can all go to infinity ( ) so there an infinite number of shapes and sizes of orbitals… we’ll consider only a few… shape (determined by l) s p d f orientation(s) (limited by m)

Schrodinger’s orbitals orld w summary umof shapes t n es a p u a q h s e in th certain (determined by l) ed w onlyshape o l l a s p spherical in only the q cer uantu tain mw orld o r i orientation(s) (limited aby m) e llow n ed tation s dumbbell / figure 8 2 “lobes” d double dumbbell / 4 -leaf clover 4 “lobes” f 8 -leaf clover 8 “lobes” ns o i t a t orien place e s e nt f th e o r e h f c ea dif a s e ib ce descr in spa orbital nt e r e f f = di

Schrodinger’s orbitals ld r o summary wof shapes s m e u t p uan in sha q he shape ta (determined by l) t r d e n i e c w y o l l l n a o s spherical in th only e qua ntum cert ain wor o ld r orientation(s) (limited by am) llow ientati ons ed 1 allowed orientation 1 orbital p dumbbell / figure 8 2 “lobes” 3 allowed orientations 3 different orbitals d double dumbbell / 4 -leaf clover 4 “lobes” 5 allowed orientations / 5 different orbitals f 8 -leaf clover 8 “lobes” 7 allowed orientations / 7 different orbitals

each shape (of orbital) comes in multiple sizes (determined by n) n shapes (# orientations) 5 4 r e larg 3 2 1 e- closer to the nucleus more stable… lower in energy total #orbitals