Chapter 4 Duality Theory q Linear Programming 2015








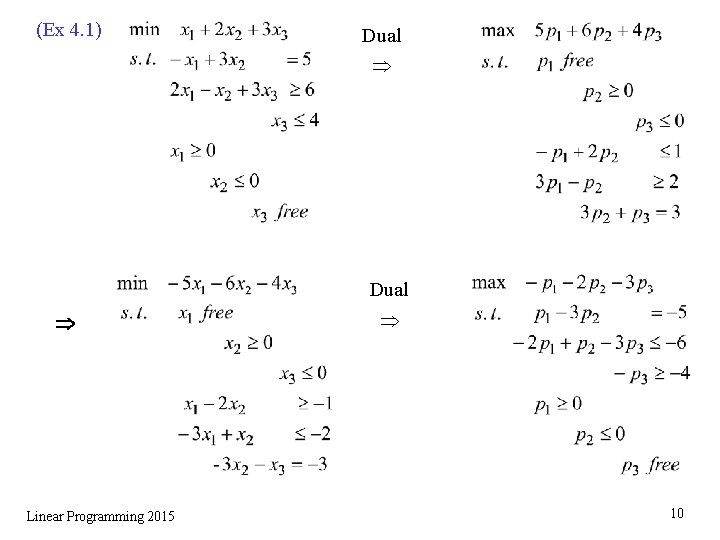












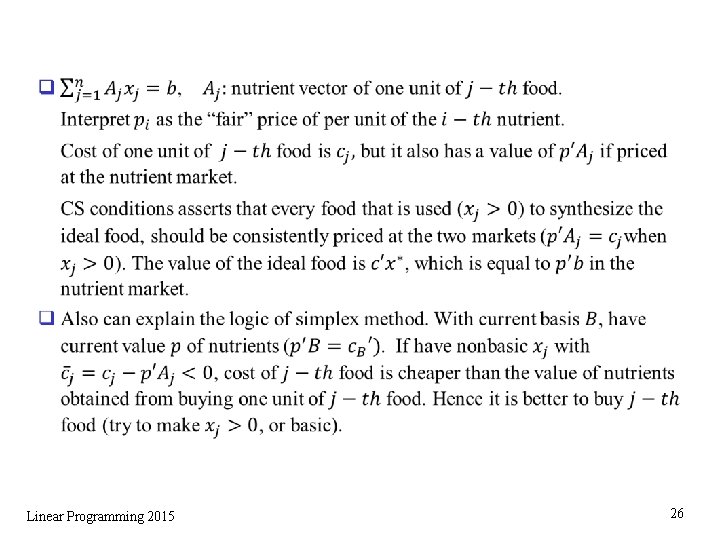











- Slides: 38

Chapter 4. Duality Theory q Linear Programming 2015 1

q Linear Programming 2015 2

q Linear Programming 2015 3

q Linear Programming 2015 4

q Linear Programming 2015 5

q Linear Programming 2015 6

4. 2 The dual problem Linear Programming 2015 7

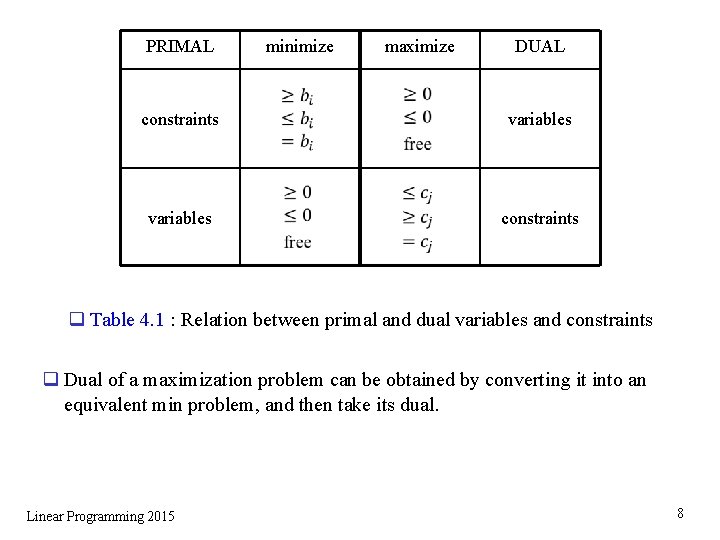
PRIMAL minimize maximize DUAL constraints variables constraints q Table 4. 1 : Relation between primal and dual variables and constraints q Dual of a maximization problem can be obtained by converting it into an equivalent min problem, and then take its dual. Linear Programming 2015 8

q Linear Programming 2015 9
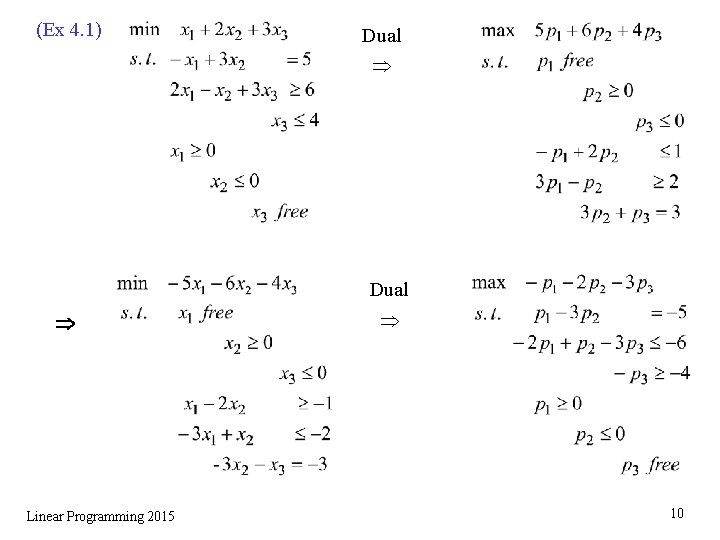
(Ex 4. 1) Dual Linear Programming 2015 10

q Linear Programming 2015 11

q Linear Programming 2015 12

q Thm 4. 2 : If we use the following transformations, the corresponding duals are equivalent, i. e. , they are either both infeasible or they have the same optimal cost. (a) free variable difference of two nonnegative variables (b) inequality by using nonnegative slack var. (c) If LP in standard form (feasible) has redundant equality constraints, eliminate them. Linear Programming 2015 13

4. 3 The duality theorem q Linear Programming 2015 14

q Linear Programming 2015 15

1 Duals of equivalent problems are equivalent Equivalent 2 Duality for standard form problems Fig 4. 1 : Proof of the duality theorem for general LP Linear Programming 2015 16

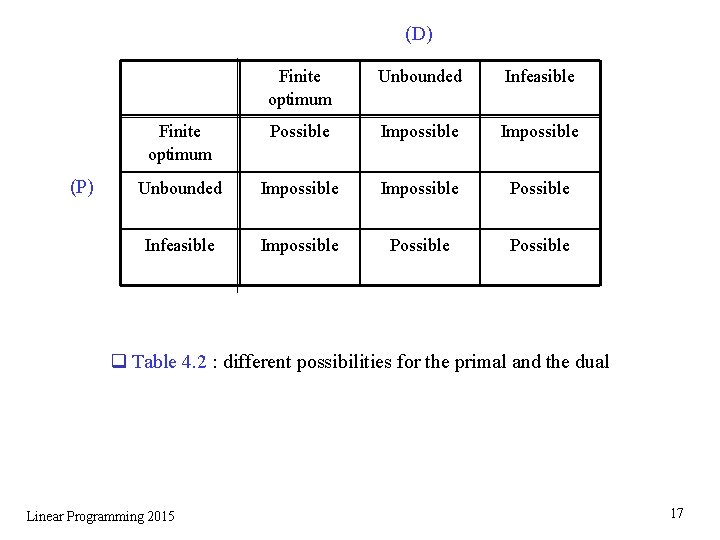
(D) (P) Finite optimum Unbounded Infeasible Finite optimum Possible Impossible Unbounded Impossible Possible Infeasible Impossible Possible q Table 4. 2 : different possibilities for the primal and the dual Linear Programming 2015 17

q Note: (1) Later, we will show strong duality without using simplex method. (see example 4. 4 later) (2) Optimal dual solution provides “certificate of optimality” certificate of optimality is (short) information that can be used to check the optimality of a given solution in polynomial time. ( Two view points : 1. Finding the optimal solution. 2. Proving that a given solution is optimal. For computational complexity of a problem, the two view points usually give the same complexity (though not proven yet, P = NP ? ). Hence, researchers were almost sure that LP can be solved in polynomial time even before the discovery of a polynomial time algorithm for LP. ) (3) The nine possibilities in Table 4. 2 can be used importantly in determining the status of primal or dual problem. Linear Programming 2015 18

q Linear Programming 2015 19

q Linear Programming 2015 20

Geometric view of optimal dual solution q Linear Programming 2015 21

q Linear Programming 2015 22

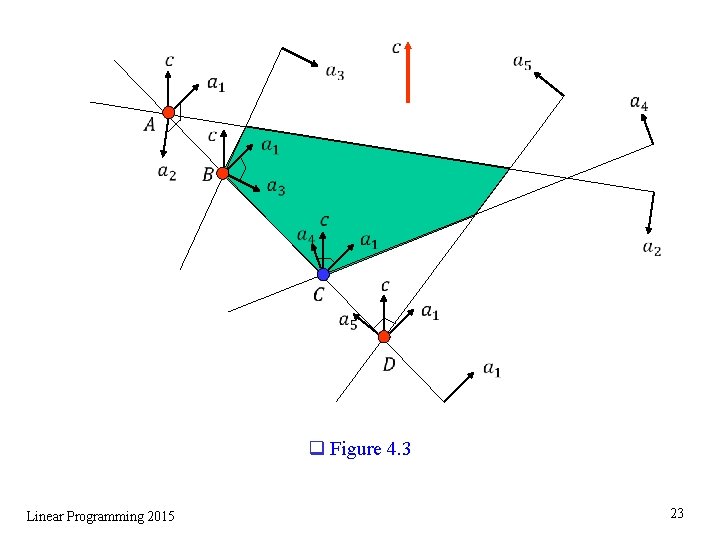
q Figure 4. 3 Linear Programming 2015 23

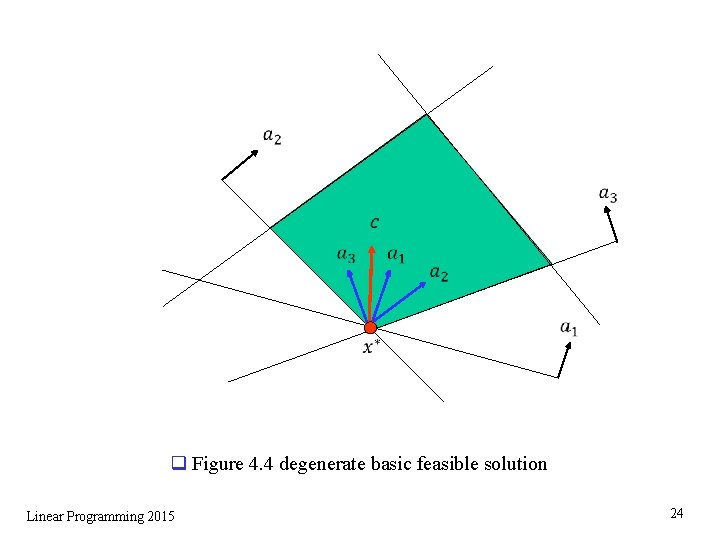
q Figure 4. 4 degenerate basic feasible solution Linear Programming 2015 24

4. 4 Optimal dual var as marginal costs q Linear Programming 2015 25
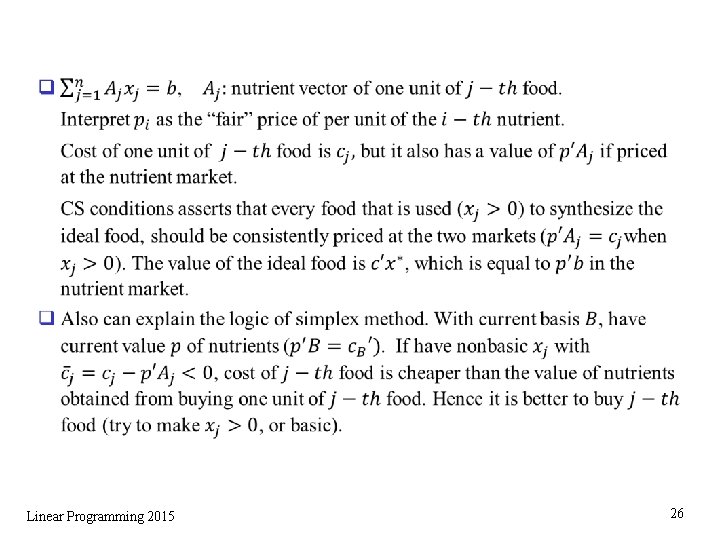
q Linear Programming 2015 26

4. 5 Dual simplex method q Linear Programming 2015 27

q Linear Programming 2015 28

q Ex 4. 7 : Linear Programming 2015 29

q Linear Programming 2015 30

q Linear Programming 2015 31

q Linear Programming 2015 32

The geometry of the dual simplex method q Linear Programming 2015 33

4. 6 Farkas’ lemma and linear inequalities q Linear Programming 2015 34

q Linear Programming 2015 35

The duality theorem revisited q Linear Programming 2015 36

q Linear Programming 2015 37

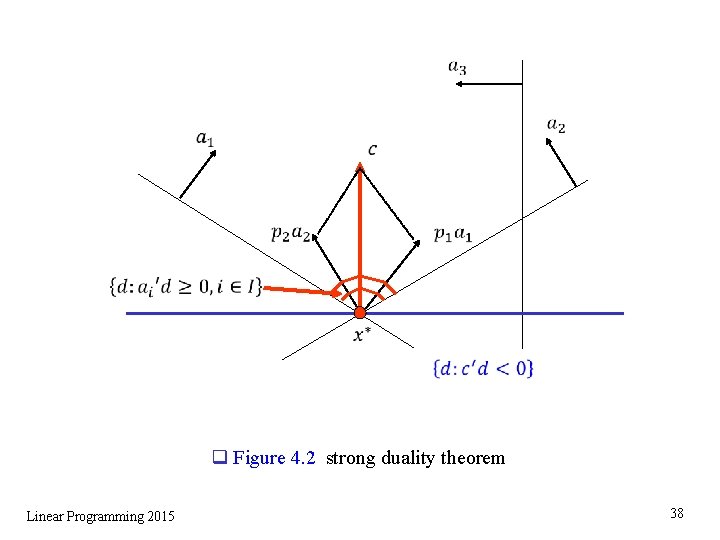
q Figure 4. 2 strong duality theorem Linear Programming 2015 38