Chapter 4 Discrete Random Variables A random variable

Chapter 4. Discrete Random Variables A random variable is a way of recording a quantitative variable of a random experiment. A variable which can take on only finitely many different values is called discrete. Example: The number of girls in a family of 8 children Example: The number of seeds which successfully germinate when 50 seeds are planted

Continuous random variables • A random variable which can take on any value (ie, all values) in a certain interval is called a continuous random variable. • EX. The height in centimeters of a 16 year old Canadian male. • Ex. The dosage in ml. of a certain pain killer

Example • Let 3 coins be tossed and let x denote the number of heads • Possible values for x are 0, 1, 2, and 3, • As done earlier, it is easy to compute • Pr(0) = 1/8, Pr(3) = 1/8, and Pr(1) = Pr(2) = 3/8 • Notation: We will also use the notation • P(x = 0) = 1/8, and so on.

Properties of Probability, P( X = xi )

Definition Copyright © 2013 Pearson Education, Inc. .

Example Graph the probability distribution of the random variable obtained by flipping an unbiased coin two times and counting the number of times heads comes up.

Solution • Possible values of x are 0, 1, 2, and a quick check shows P(0) = ¼, P(1) = 1/2, and P(2) = ¼.
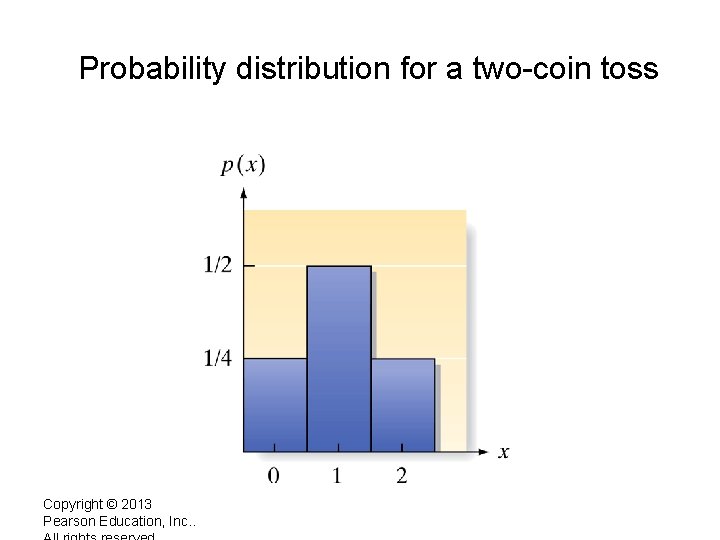
Probability distribution for a two-coin toss Copyright © 2013 Pearson Education, Inc. .

Definition Copyright © 2013 Pearson Education, Inc. .

Definition Copyright © 2013 Pearson Education, Inc. .

Definition Copyright © 2013 Pearson Education, Inc. .

Procedure Copyright © 2013 Pearson Education, Inc. .
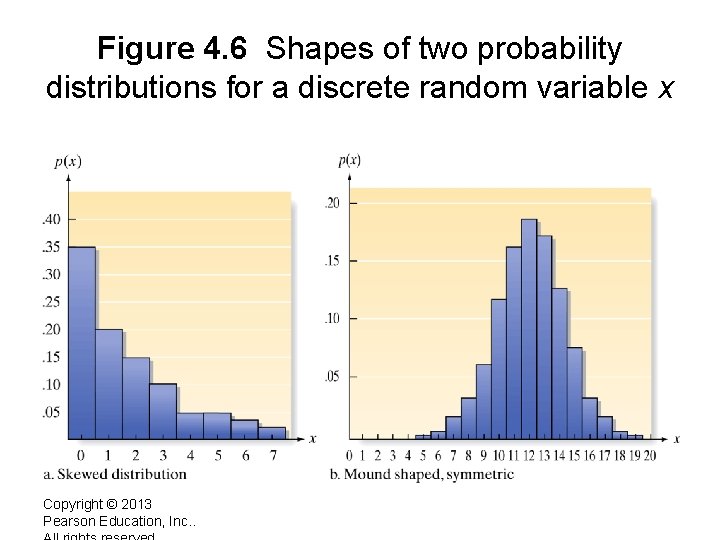
Figure 4. 6 Shapes of two probability distributions for a discrete random variable x Copyright © 2013 Pearson Education, Inc. .

Example • Medical research shows a certain type of chemotherapy is successful 70% of the time. Suppose 5 patients are treated and let x denote the number of successes. One can show • x 0 1 2 3 4 5 P(x) . 002 . 029 . 132 . 309 . 360 . 168
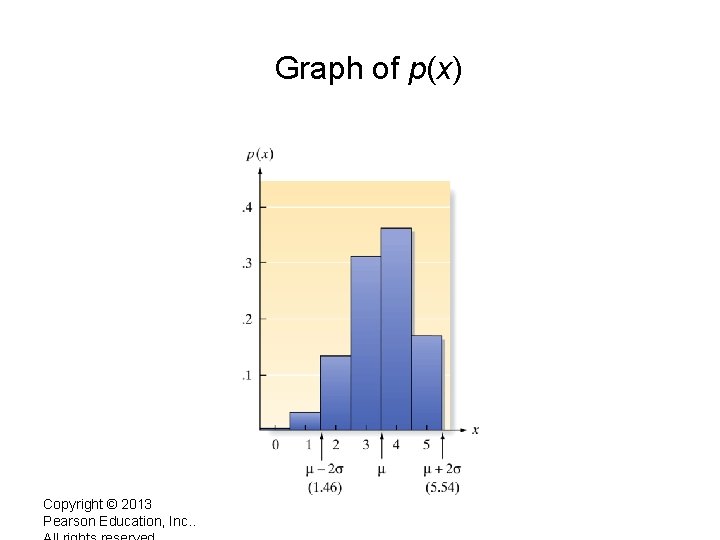
Graph of p(x) Copyright © 2013 Pearson Education, Inc. .

Find the mean and interpret • Applying the formulae we obtain • Mean = 3. 50 • Consider a large number of trials, each consisting of treating 5 patients. On average, the number of successes will be 3. 5. Thus, if 200 trials each of 5 patients is conducted, we would expect and average of 3. 5 successes per trial for a total of 700 successes for 1000 patients

Find the standard deviation and interpret • Using the formula you can check that • Standard deviation = 1. 02. • Using Empirical Rule, would expect that approximately 68% of times the trial is repeated, the outcome will be between 3. 5 -1. 02 and 3. 5+1. 02, i. e. , will lie in the interval [2. 48, 4. 52]. • What is the actual percentage of times the outcome will be in that interval?

Binomial Experiment A binomial experiment is one that: 1) Has a fixed number of trials (n) 2) These trials are independent 3) Each trial must have all outcomes classified into two categories (Success or Failure) 4) The probability of success remains constant for all trials.

Notation: • • • S = success and P(S) = p F = Failure and P(F) = q = 1 - p n = fixed number of trials x = specific number of successes in n trials P(x) = the probability of getting exactly x successes among n trials

Factorials 0! = 1 1! = 1 2! = 2 * 1 3! = 3 * 2 * 1 4! = 4* 3 * 2 * 1 n! = n*(n-1)!

Factorials 0! = 1 1! = 1 2! = 2 * 1=2 3! = 3 * 2 * 1=6 4! = 4* 3 * 2 * 1=24 n! = n*(n-1)!

Binomial Probability Distribution In a binomial experiment, with constant probability p of success at each trial, the probability of x successes in n trials is given by

Example Shaq is a basketball player who takes a lot of free throws. The probability of Shaq making a free throw is 0. 60 on each throw. With 3 free throws what is the probability that he makes 2 shots?

Example Shaq is a basketball player who takes a lot of free throws. The probability of Shaq making a free throw is 0. 60 on each throw. With 3 free throws what is the probability that he makes 2 shots?

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.
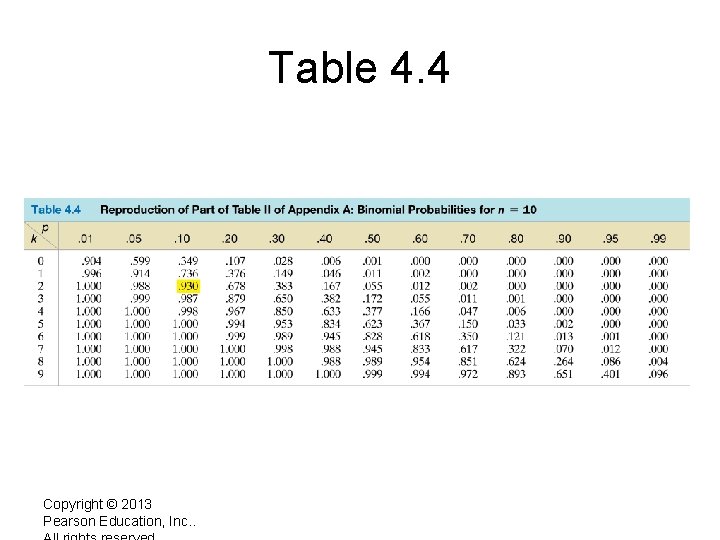
Table 4. 4 Copyright © 2013 Pearson Education, Inc. .

How to use the Binomial Tables • First find the appropriate table for the particular value of n • then find the value of p in the top row • Find the row corresponding to k and find the intersection with the column corresponding to the value of p • The value you obtain is the cumulative probability, that is P(x ≤ k) • N=10, p = 0. 7: P(x ≤ 4) = 0. 047 • N=10, p = 0. 7: P(x = 4) = P(x ≤ 4) - P(x ≤ 3) = 0. 047 -0. 011=0. 036 • N=10, p = 0. 7: P(x > 4) = 1 - P(x ≤ 4) = 1 - 0. 047 = 0. 953

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Example Flipping a biased coin 8 times. The probability of heads on each trial is 0. 4. What is the probability of obtaining at least 2 heads.

Mean and Standard deviation

Keys to success Learn the binomial table. Be able to recognize binomial distributions and when you do apply the appropriate formulas and tables.
- Slides: 37