CHAPTER 4 DIFFERENTIATION NazuhusnaMicroelektronicUNIMAP 1 08 March 2021
















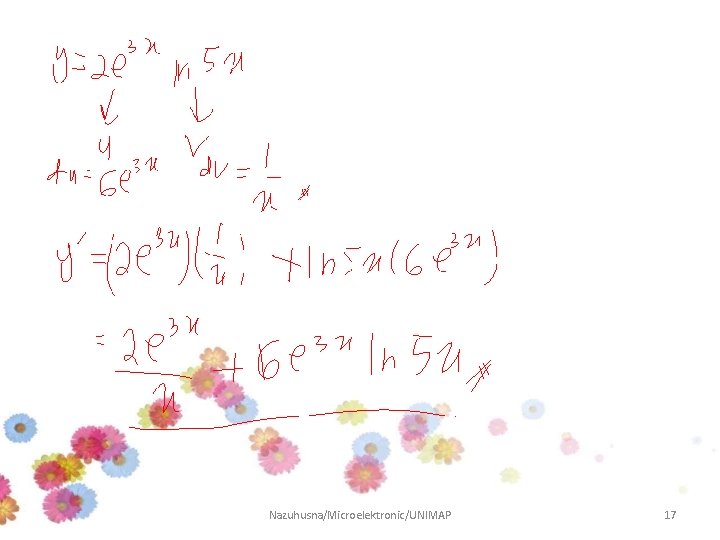


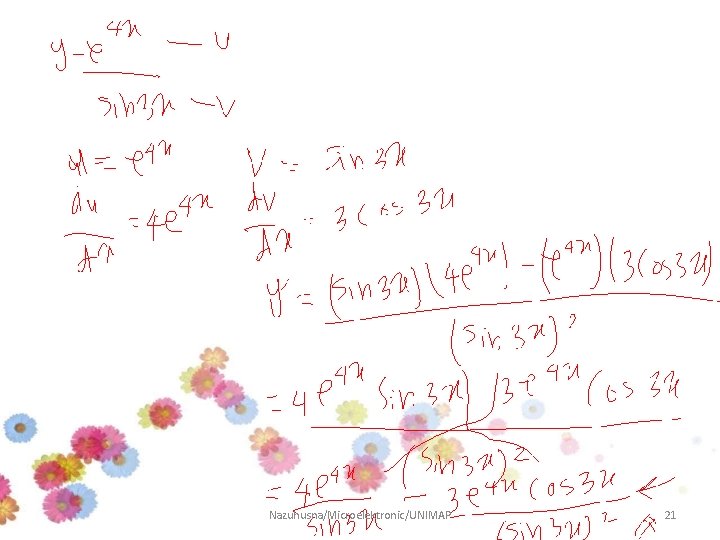

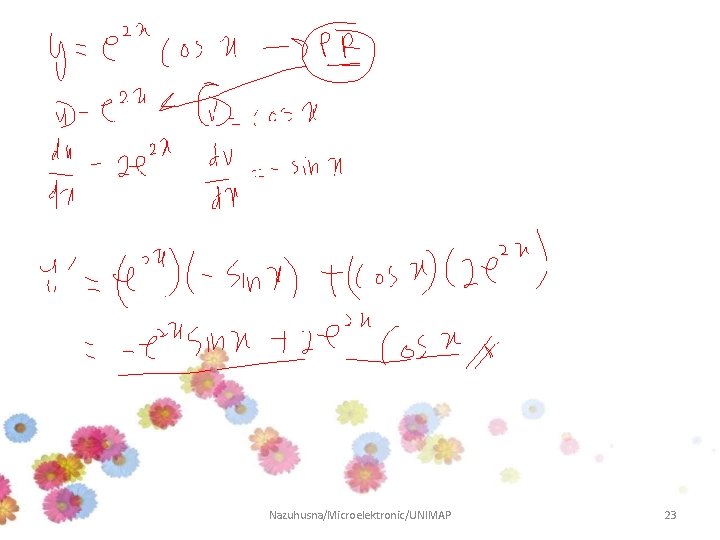
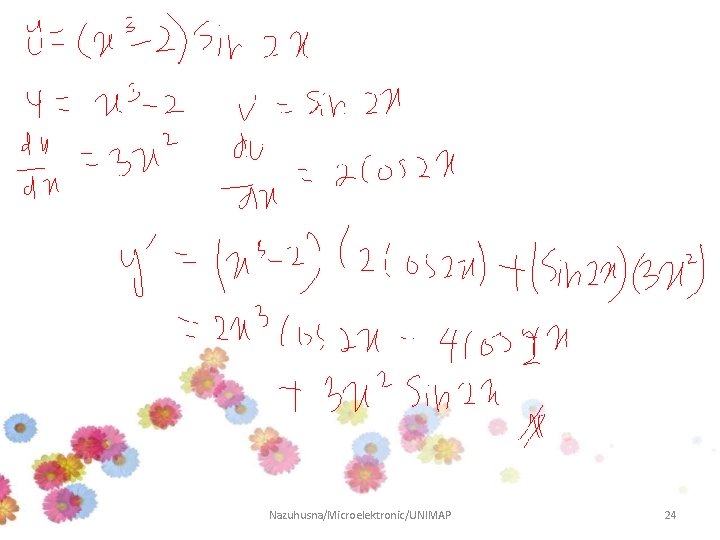
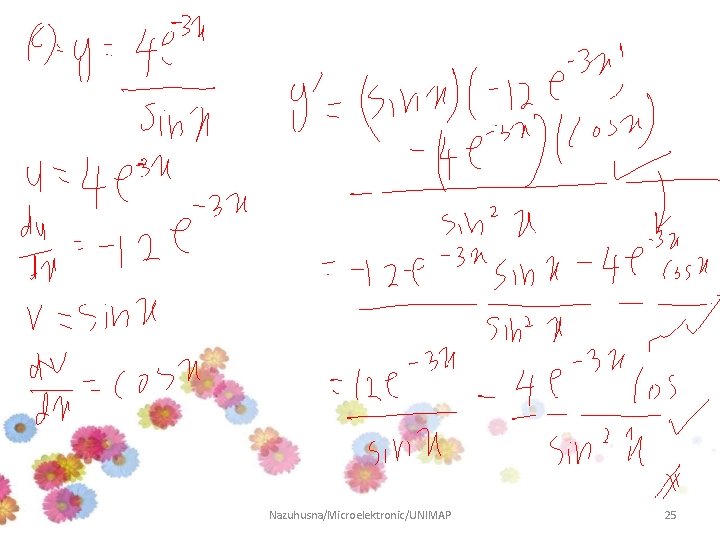
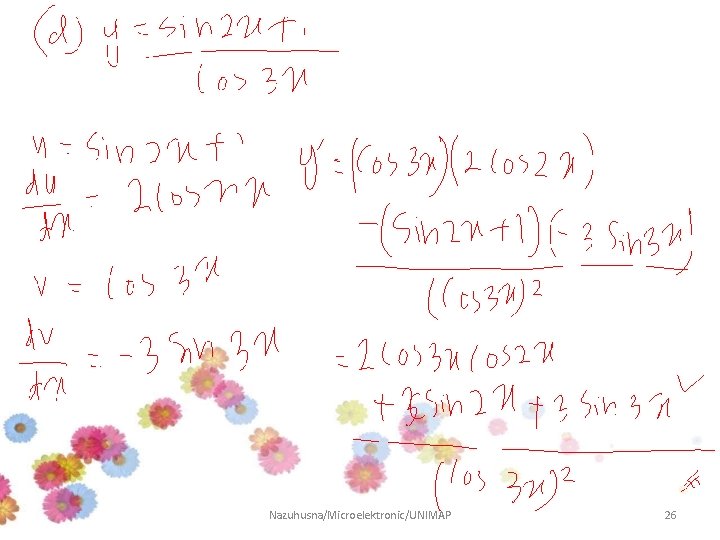




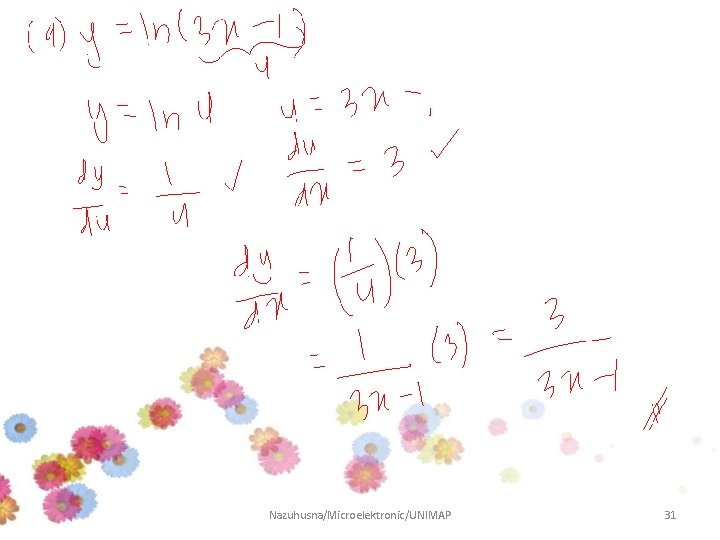
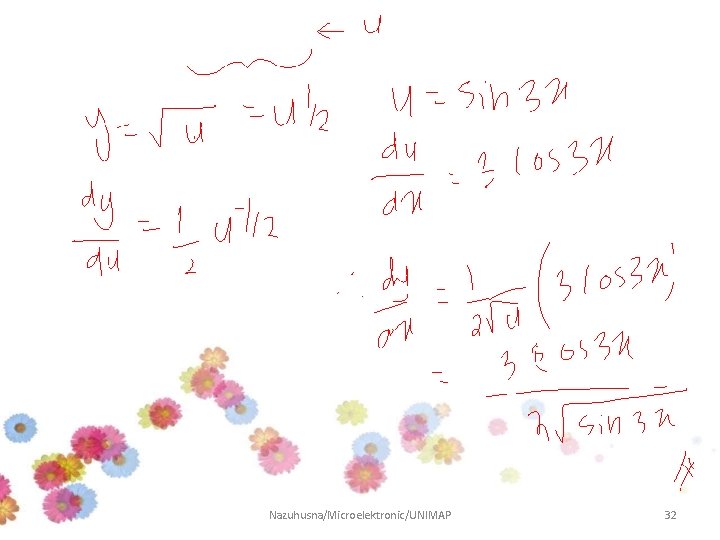





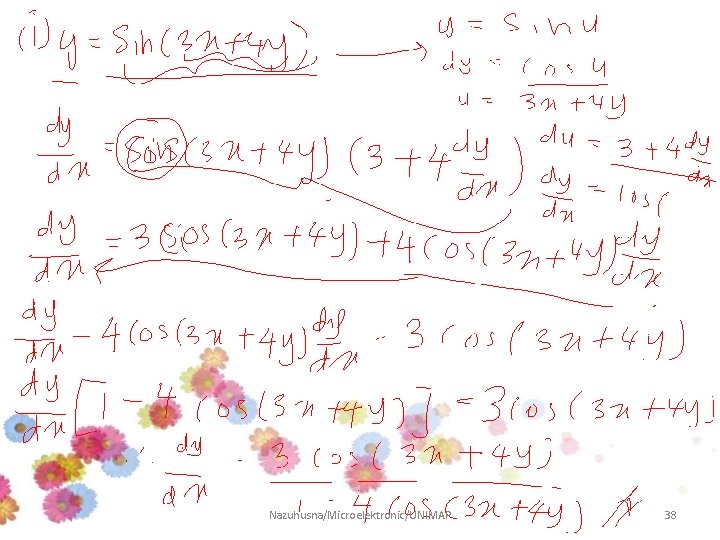
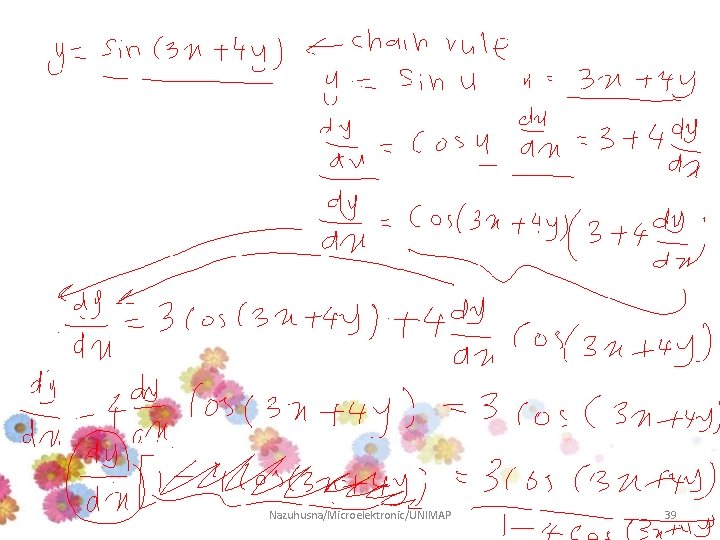
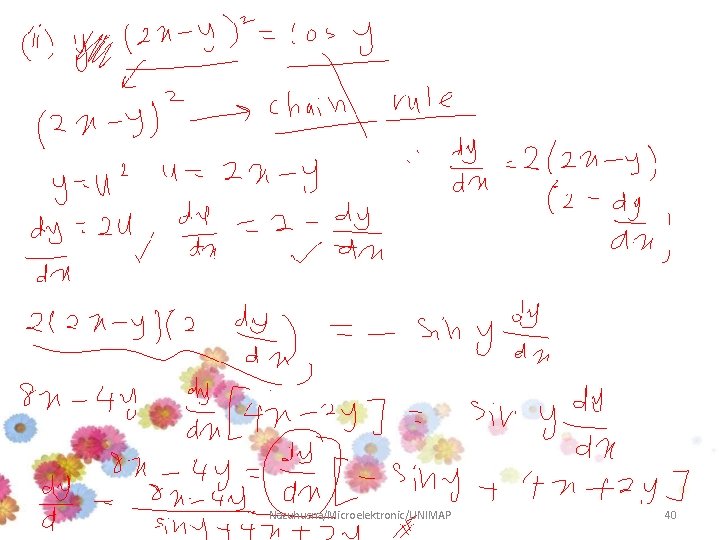
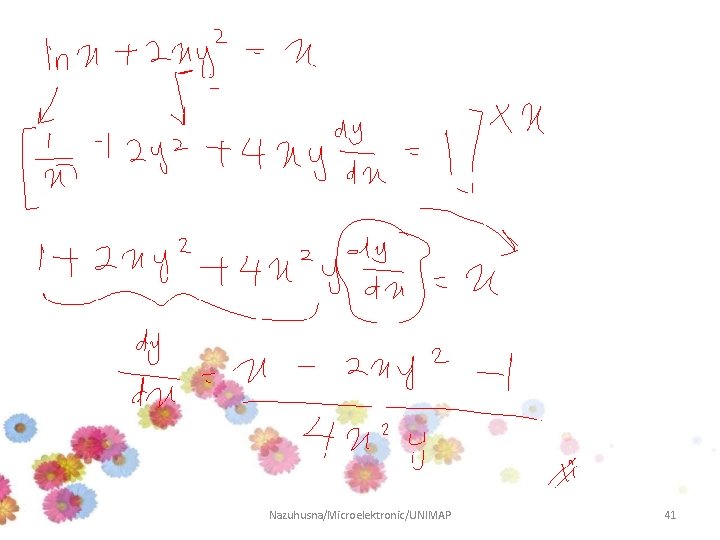
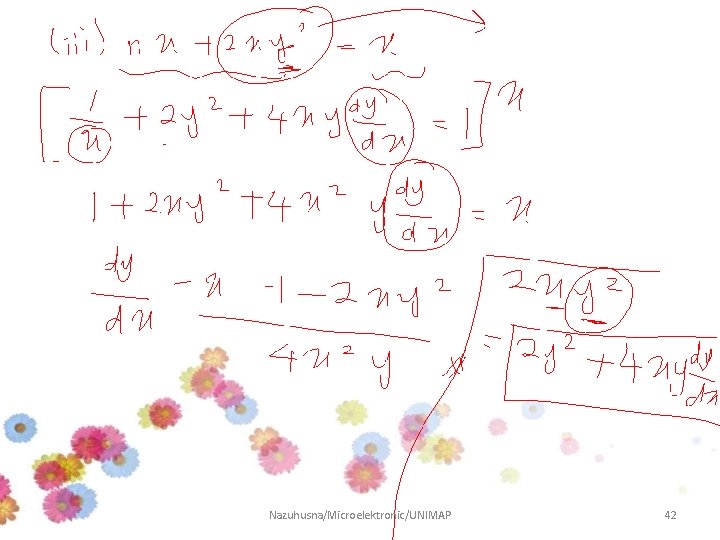

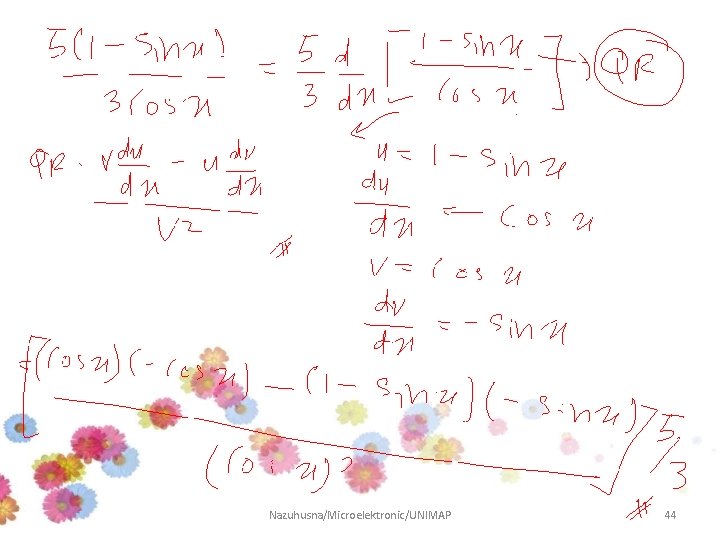


















![1 st DERIVATIVE TEST Suppose that f is continuous on [a, b] and differentiable 1 st DERIVATIVE TEST Suppose that f is continuous on [a, b] and differentiable](https://slidetodoc.com/presentation_image_h/2de582be0c3b27a05f7012490751b668/image-67.jpg)




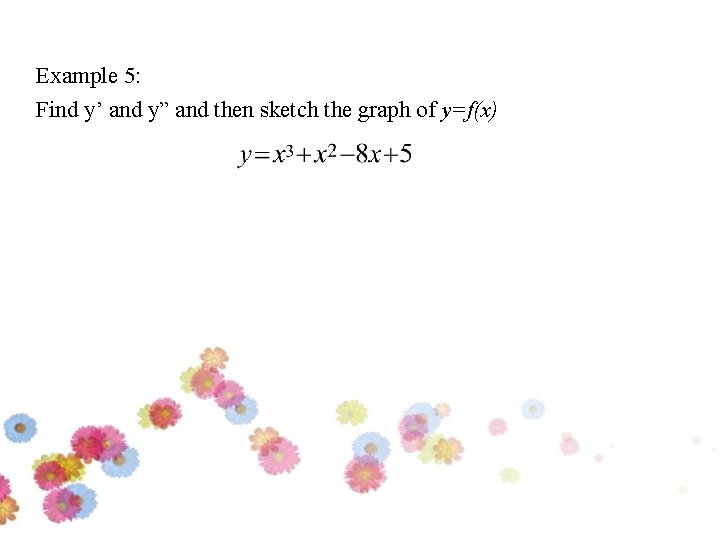





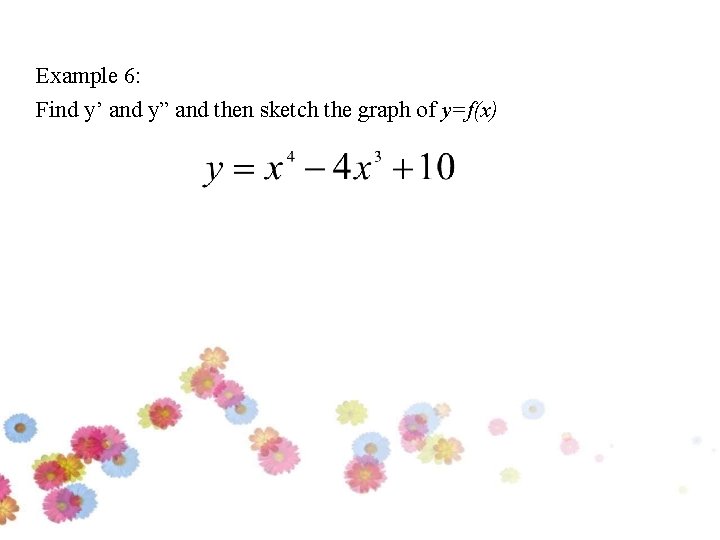
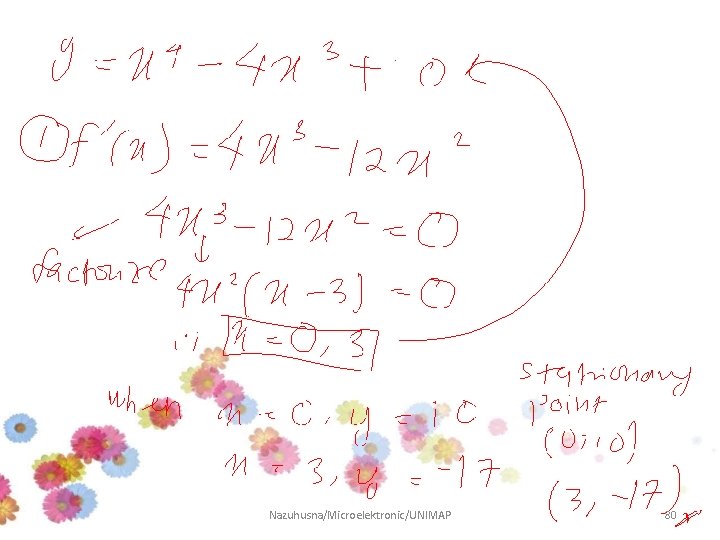
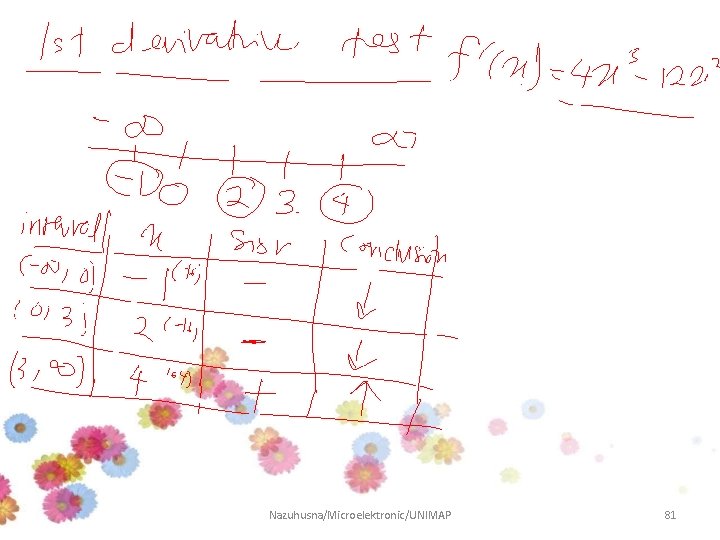


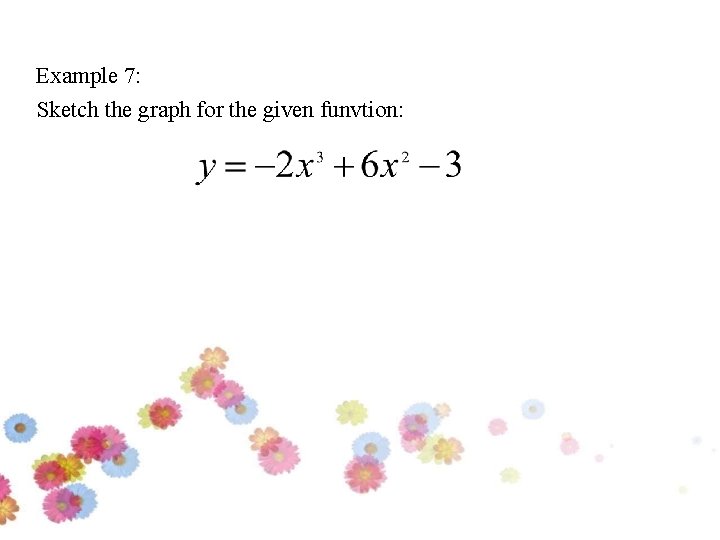




- Slides: 94

CHAPTER 4 DIFFERENTIATION Nazuhusna/Microelektronic/UNIMAP 1

08 March 2021 School of Microelectronic 2

INTRODUCTION • Differentiation – Process of finding the derivative of a function. • Notation Nazuhusna/Microelektronic/UNIMAP 3

DERIVATIVE OF A POWER FUNCTION • If n is an integer, then: Nazuhusna/Microelektronic/UNIMAP 4

DERIVATIVE OF A CONSTANT If f is differentiable at function x and c is any real number, then c is differentiable: Nazuhusna/Microelektronic/UNIMAP 5

Example • Find dy/dx in the following cases: Solution (i) Nazuhusna/Microelektronic/UNIMAP Solution (ii) 6

Example 1 Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 7

DERIVATIVE OF SUM AND DIFFERENCE RULES If f and g are differentiable at function x, then the function f+g and fg are differentiable: Nazuhusna/Microelektronic/UNIMAP 8

Example • Differentiate Solution Nazuhusna/Microelektronic/UNIMAP 9

Example 2 Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 10

Derivative of Trigonometric Functions Nazuhusna/Microelektronic/UNIMAP 11

DERIVATIVE OF EXPONENTIAL & LOGARITHMIC FUNCTIONS Nazuhusna/Microelektronic/UNIMAP 12

PRODUCT RULE If u and v are differentiable at function x, then so the product u. v, thus Nazuhusna/Microelektronic/UNIMAP 13

Example • Differentiate Solution Nazuhusna/Microelektronic/UNIMAP 14

Past Exam Question Nazuhusna/Microelektronic/UNIMAP 15

Example 3: Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 16
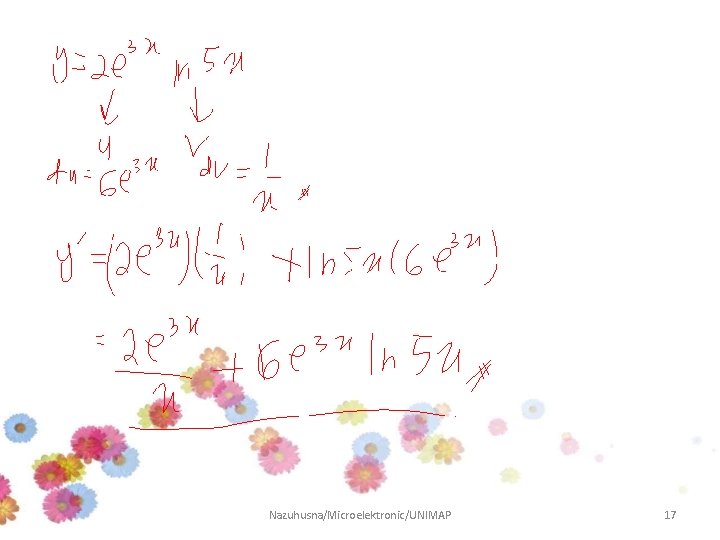
Nazuhusna/Microelektronic/UNIMAP 17

QUOTIENT RULE If u and v are differentiable at function x, then is also differentiable Nazuhusna/Microelektronic/UNIMAP 18

Example • Differentiate Solution Nazuhusna/Microelektronic/UNIMAP 19

Example 4 Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 20
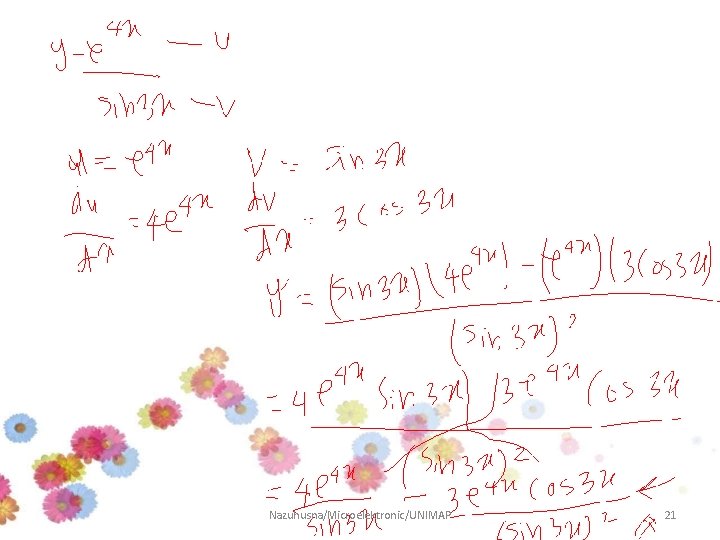
Nazuhusna/Microelektronic/UNIMAP 21

Example 5 Differentiate and SIMPLIFY the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 22
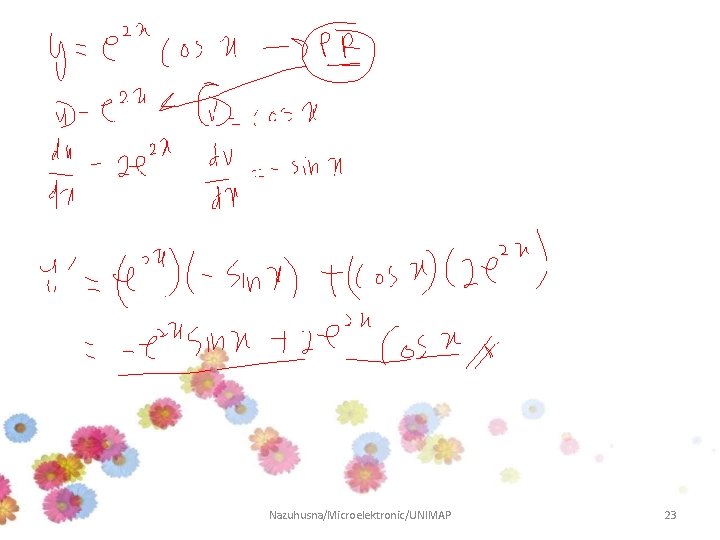
Nazuhusna/Microelektronic/UNIMAP 23
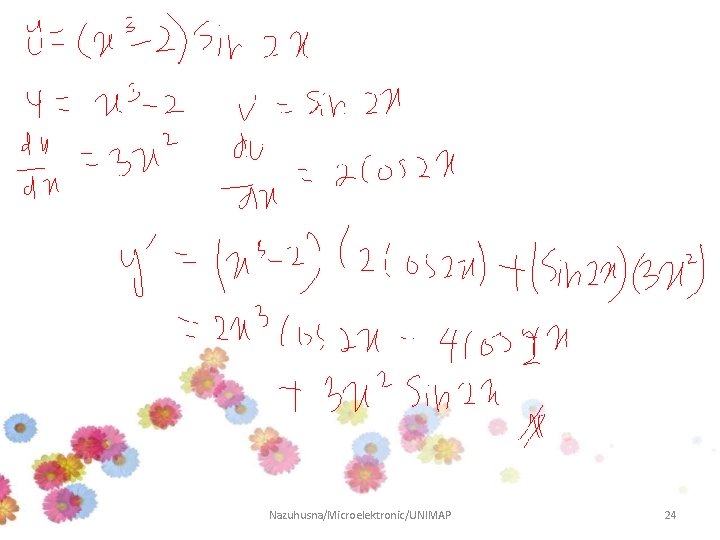
Nazuhusna/Microelektronic/UNIMAP 24
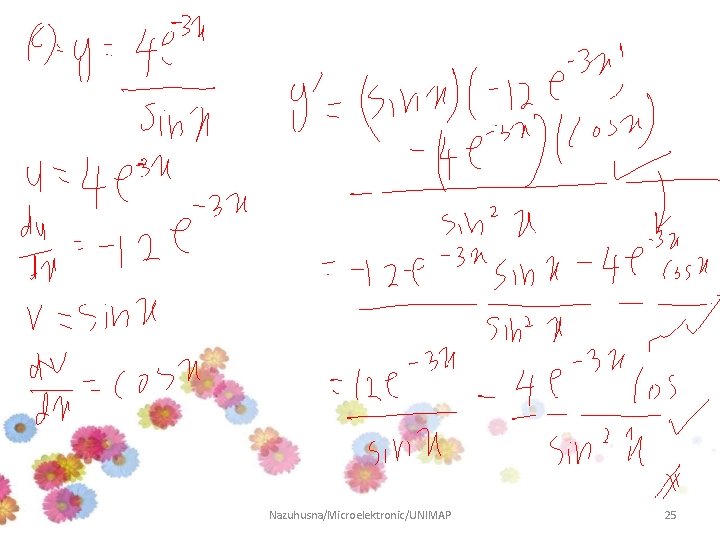
Nazuhusna/Microelektronic/UNIMAP 25
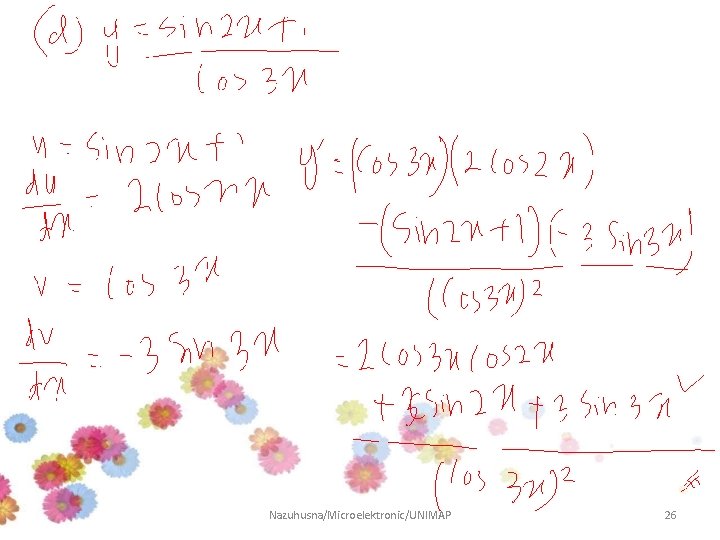
Nazuhusna/Microelektronic/UNIMAP 26

Example 6 Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 27

The Chain Rule – If g is differentiable at point x and f is differentiable at the point g(x), then is differentiable at x. – Let and , then Nazuhusna/Microelektronic/UNIMAP 28

Example • Differentiate Solution Nazuhusna/Microelektronic/UNIMAP 29

Example 7 Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 30
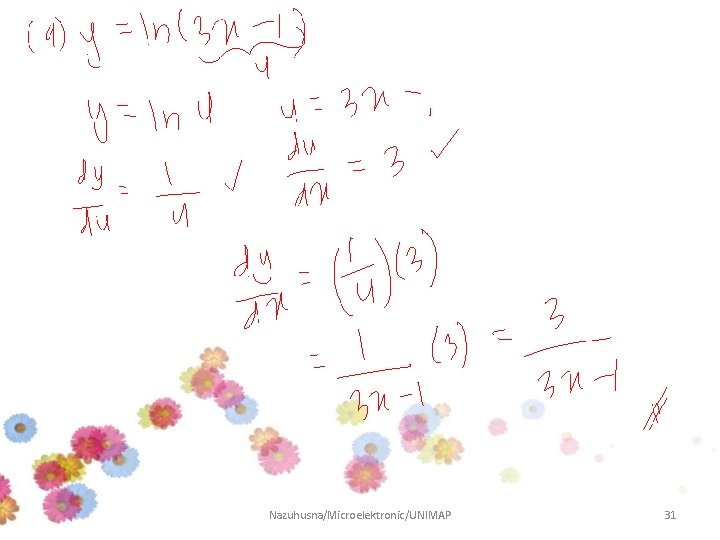
Nazuhusna/Microelektronic/UNIMAP 31
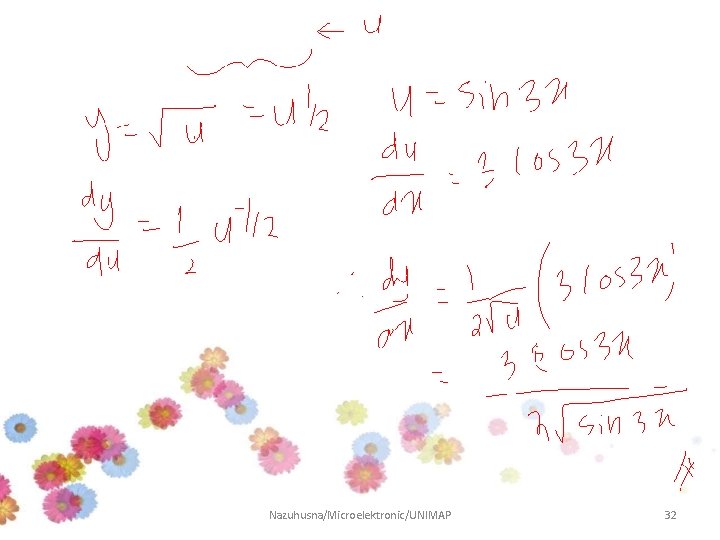
Nazuhusna/Microelektronic/UNIMAP 32

Example 8 Differentiate the following function: Answer: Nazuhusna/Microelektronic/UNIMAP 33

IMPLICIT DIFFERENTIATION • These equation define an implicit relation between variables x and y. • When we cannot put an equation F(x, y)=0 in the form y = f(x), use implicit differentiation to find Nazuhusna/Microelektronic/UNIMAP 34

IMPLICIT DIFFERENTIATION • Differentiate both sides of the equation with respect to x, treating y as a differentiable function of x • Collect the terms with on one side of the equation • Solve for Nazuhusna/Microelektronic/UNIMAP 35

Example • Use implicit differentiation to find y’ if: Solution Nazuhusna/Microelektronic/UNIMAP 36

Example • Use implicit differentiation to find if: Answer Nazuhusna/Microelektronic/UNIMAP 37
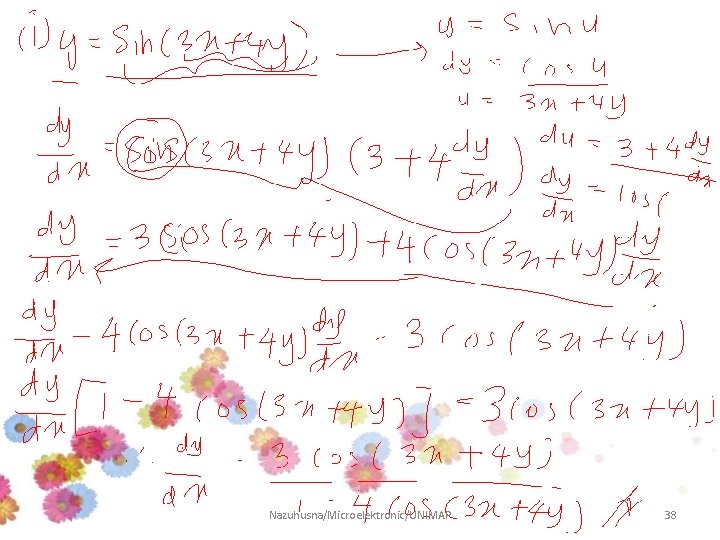
Nazuhusna/Microelektronic/UNIMAP 38
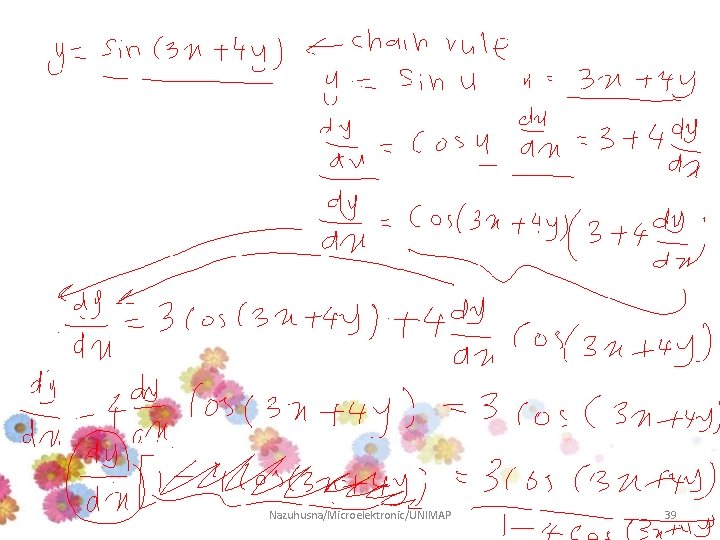
Nazuhusna/Microelektronic/UNIMAP 39
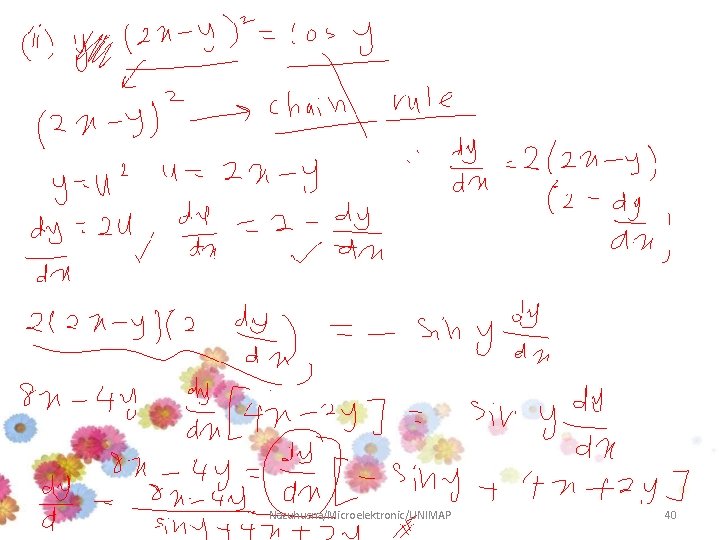
Nazuhusna/Microelektronic/UNIMAP 40
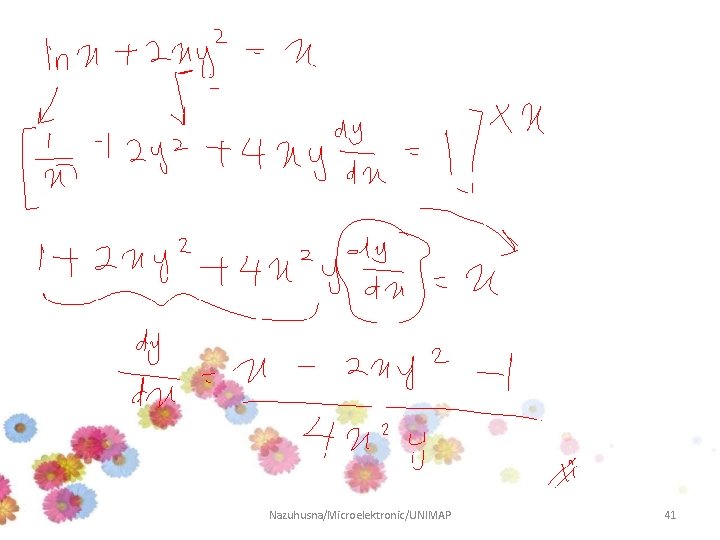
Nazuhusna/Microelektronic/UNIMAP 41
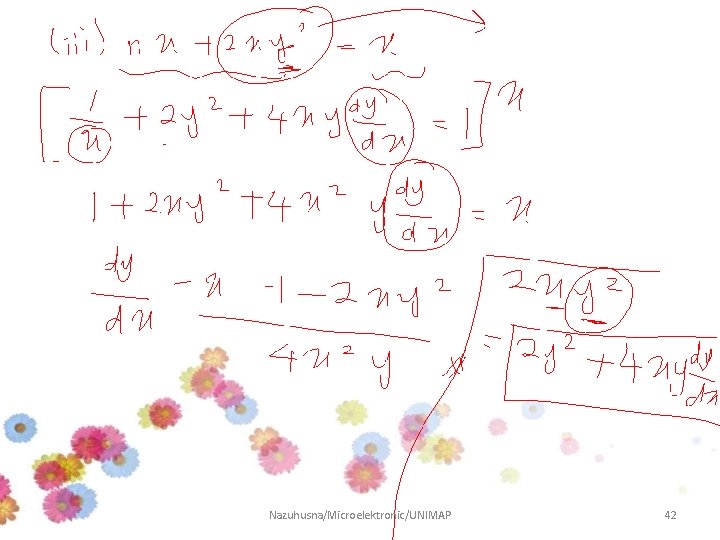
Nazuhusna/Microelektronic/UNIMAP 42

Past Exam Question Nazuhusna/Microelektronic/UNIMAP 43
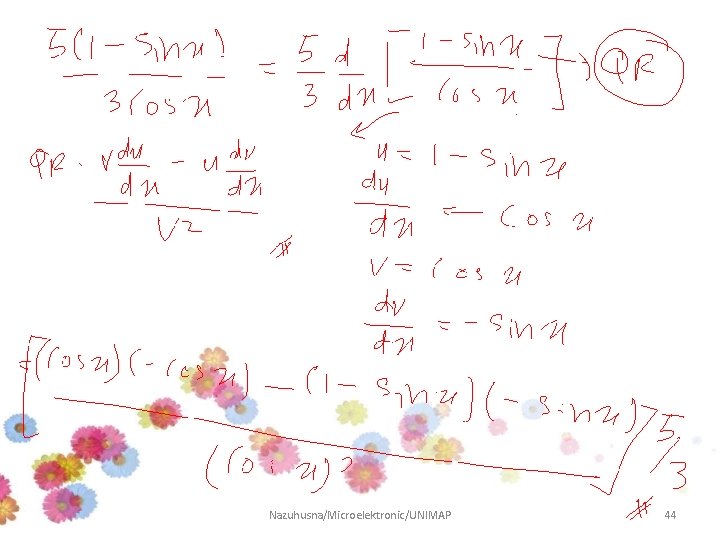
Nazuhusna/Microelektronic/UNIMAP 44

Nazuhusna/Microelektronic/UNIMAP 45

CHAPTER 4 APPLICATION: (I) TANGENT LINE (II) RELATED RATES (III)MINIMUM AND MAXIMUM VALUES

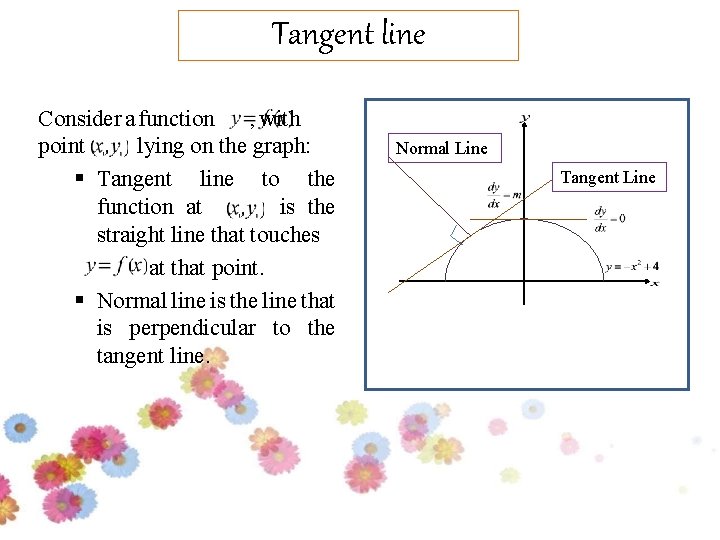
Tangent line Consider a function , with point lying on the graph: § Tangent line to the function at is the straight line that touches at that point. § Normal line is the line that is perpendicular to the tangent line. Normal Line Tangent Line

• Tangent Line Equation: or • Normal Line Equation: or

Example 1: 1. Find the slope of the curve at the given points 2. Find the lines that are tangent and normal to the curve at the given point.

RELATED RATES • In this section we are going to look at an application of implicit differentiation. • The first reason is that it’s an application of implicit differentiation and so putting it right after that section means that we won’t have forgotten how to do implicit differentiation. • The other reason is simply that after doing all these derivatives we need to be reminded that there really are actual applications to derivatives. • Sometimes it is easy to forget there really is a reason that we’re spending all this time on derivatives. • For these related rates problems it’s usually best to just jump right into some problems and see how they work. • A process of finding a rate at which a quantity changes by relating that quantity to the other quantities. • The rate is usually with respect to time, t.

Example 2 Suppose that the radius, r and area, of a circle are differentiable functions of t. Write an equation that relates to . Answer:

Example 3 How fast is the area of a rectangle changing from one side 10 cm long and the side increase at a rate of 2 cm/s and the other side is 8 cm long and decrease at a rate of 3 cm/s? x y

Solution: x y Differentiate (1) wrt t:

Example 4 A stone is dropped into a pond, the ripples forming concentric circles which expand. At what rate is the area of one of these circles increasing when the radius is 3 m and increasing at the rate of 0. 6 m/s?

Solution: r Differentiate wrt t :

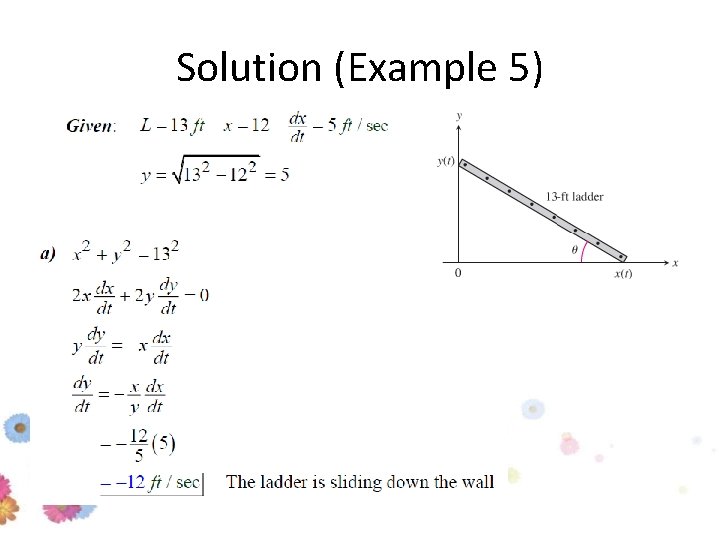
Example 5 A 13 ft ladder is leaning against a house when its base starts to slide away. By the time the base is 12 ft from the house, the base is moving at the rate of 5 ft/sec. (a) How fast is the top of the ladder sliding down the wall? (b) At what rate is the area of the triangle formed by the ladder, wall and ground changing (c) At what rate is the angle between the ladder and the ground changing?

Solution (Example 5)

(b) At what rate is the area of the triangle formed by the ladder, wall and ground changing (c) At what rate is the angle between the ladder and the ground changing?

Example 6 When a circular plate of metal is heated in an oven, its radius increases at the rate of 0. 01 cm/sec. At what rate is the plate’s area increasing when the radius is 50 cm? Step 1: r = radius of plate, A = area of plate Step 2: At the instant in question, dr/dt = 0. 01 cm/sec, r = 50 cm Step 3: Need d. A/dt Step 4:

Example 6 When a circular plate of metal is heated in an oven, its radius increases at the rate of 0. 01 cm/sec. At what rate is the plate’s area increasing when the radius is 50 cm? Step 5: Step 6: à At the instant in question, the area is increasing at the rate of

Exercise 1 The length l of a rectangle is decreasing at the rate of 2 cm/s, while the width w is increasing at the rate 2 cm/s. When l=12 cm and w=5 cm find the rates of change (a) The area (Hint: The A is the function of the l and w) (b) The perimeter

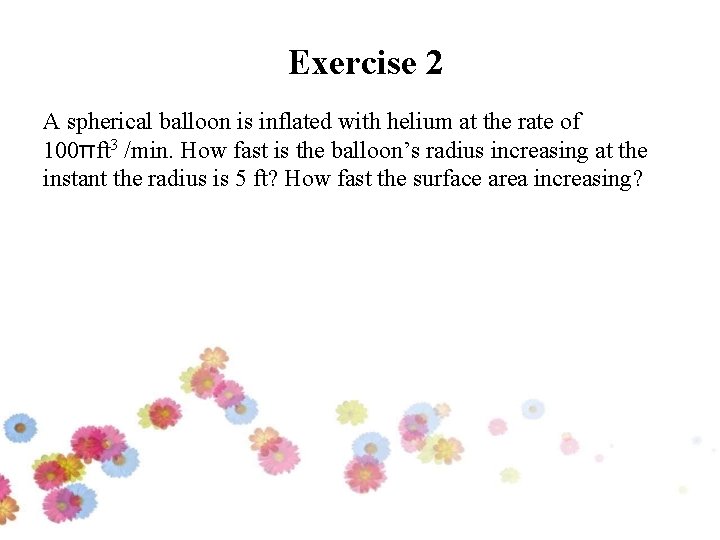
Exercise 2 A spherical balloon is inflated with helium at the rate of 100πft 3 /min. How fast is the balloon’s radius increasing at the instant the radius is 5 ft? How fast the surface area increasing?

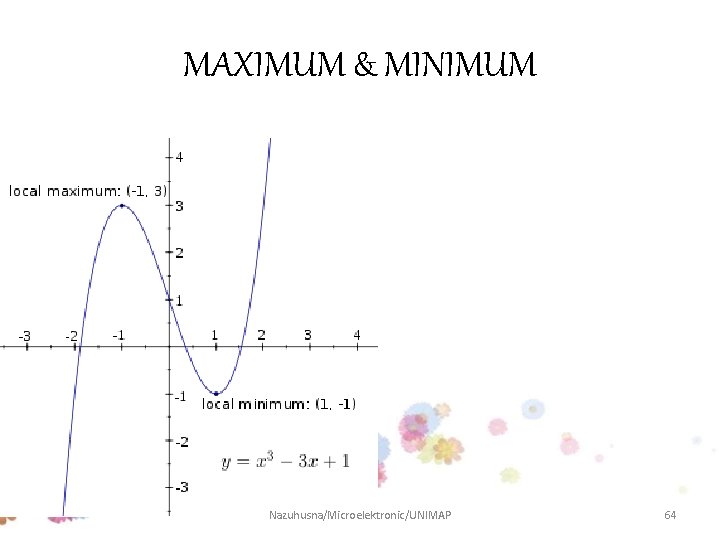
MAXIMUM & MINIMUM • Use 1 st derivative to locate and identify extreme values(stationary values) of a continuous function from its derivative Definition: Absolute Maximum and Absolute Minimum • Let f be a function with domain D. Then f has an ABSOLUTE MAXIMUM value on D at a point c if: ABSOLUTE MINIMUM

MAXIMUM & MINIMUM Nazuhusna/Microelektronic/UNIMAP 64

STATIONARY POINT • A point on the graph of a function y = f(x) where the rate of change is zero. Example 6 Find stationary points: Answer:

INCREASING & DECREASING Let f be a function defined on an interval I and let x 1 and x 2 be any two points in I 1) If f (x 1)< f (x 2) whenever x 1 < x 2, then f is said to be increasing on I 2) If f (x 1)> f (x 2) whenever x 1 < x 2, then f is said to be decreasing on I
![1 st DERIVATIVE TEST Suppose that f is continuous on a b and differentiable 1 st DERIVATIVE TEST Suppose that f is continuous on [a, b] and differentiable](https://slidetodoc.com/presentation_image_h/2de582be0c3b27a05f7012490751b668/image-67.jpg)
1 st DERIVATIVE TEST Suppose that f is continuous on [a, b] and differentiable on (a, b). 1) If f’(x)>0 at each point , then f is said to be increasing on [a, b] 2) If f’(x)<0 at each point , then f is said to be decreasing on [a, b] A method for determining whether an inflection point is a minimum, maximum, or neither.

CONCAVITY The graph of a differentiable function y=f(x) 1) Concave up on an open interval if f’ is increasing on I 2) Concave down on an open interval if f’ is decreasing on I

2 ND DERIVATIVE TEST: TEST FOR CONCAVITY Let y=f(x) be twice-differentiable on an interval I 1) If f”(x)>0 on I, the graph of f over I is concave up 2) If f”(x)<0 on I, the graph of f over I is concave down A method for determining whether a critical point is a relative minimum or maximum. Critical Point : A point (x, y) on the graph of a function at which the derivative is either 0 or undefined. A critical point will often be a minimum or maximum, but it may be neither.

MAXIMUM POINT & MINIMUM POINT • If y is minimum Therefore (x, y) is a minimum point. • If y is maximum Therefore (x, y) is a maximum point.

CONCAVITY A point where the graph of a function has a tangent line and where the concavity changes is a POINT OF INFLECTION.
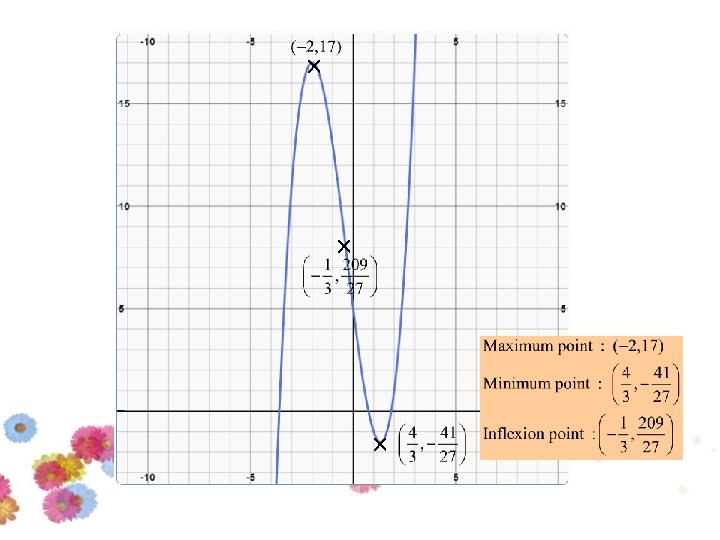
Example 5: Find y’ and y” and then sketch the graph of y=f(x)

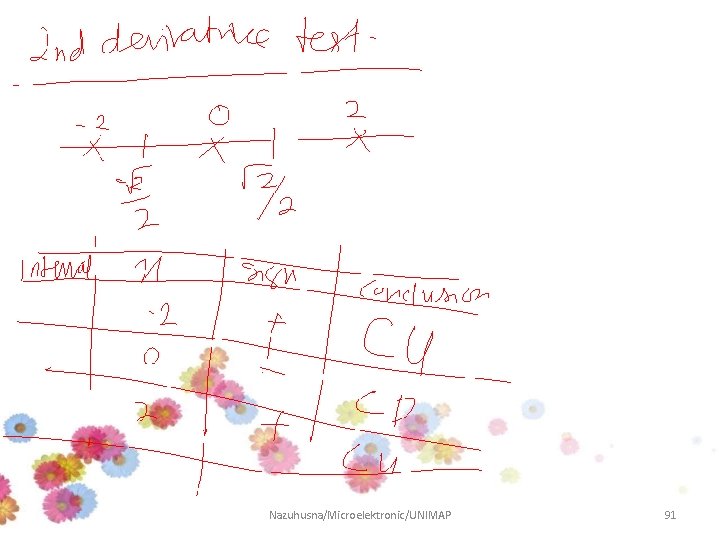
Solution: Step 1: Find the stationary point Stationary values Therefore, the stationary points are:

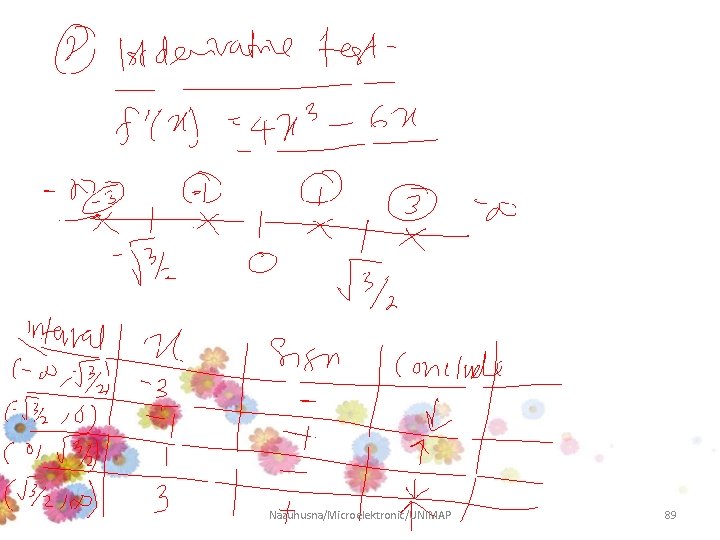
The 1 st Derivative Test Since the stationary values are : The intervals: x Table: Interval x=c Sign of Conclusion -3 + Increasing 0 - Decreasing 2 + Increasing

Step 2 : Find inflection point Therefore, the inflection points is: inflection point is where the curve changes from concave upwards to concave downwards (or vice versa)

The 2 nd Derivative Test Since the inflection value is : The intervals: x Table: Interval x=c Sign of Conclusion -2 - Concave Downwards 0 + Concave Upwards

Step 4: Test for maximum and minimum At Therefore, (-2, 17) is a maximum point. At Therefore, (4/3, -41/27) is a minimum point.

Example 6: Find y’ and y” and then sketch the graph of y=f(x)
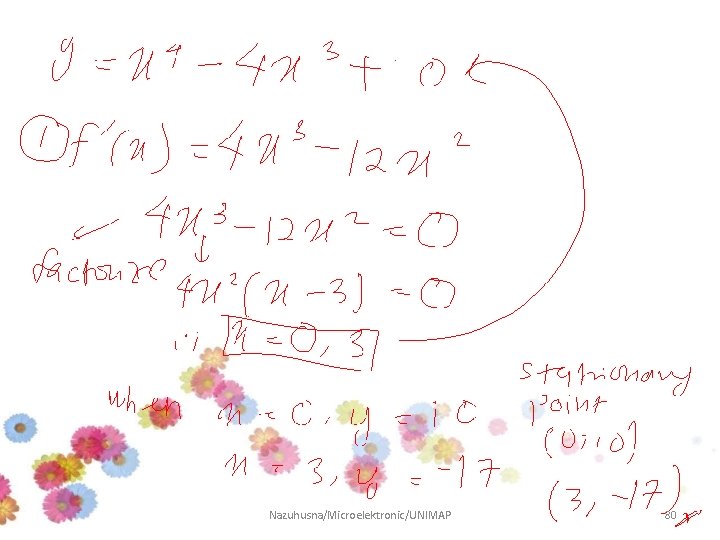
Nazuhusna/Microelektronic/UNIMAP 80
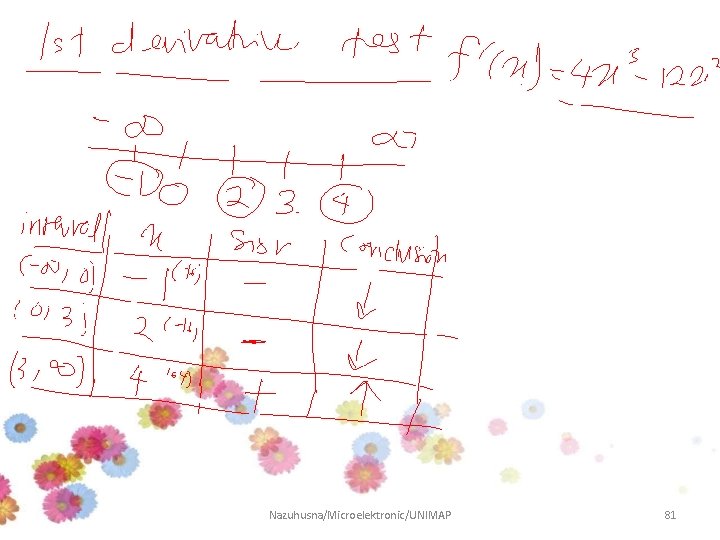
Nazuhusna/Microelektronic/UNIMAP 81

Nazuhusna/Microelektronic/UNIMAP 82

Nazuhusna/Microelektronic/UNIMAP 83

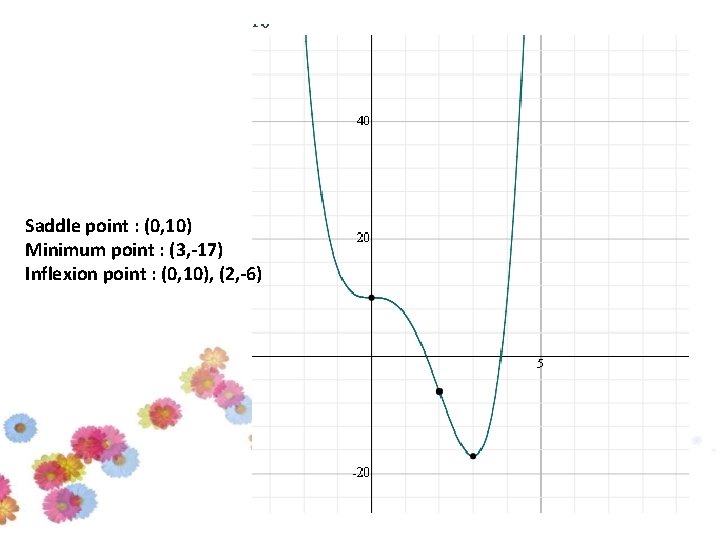
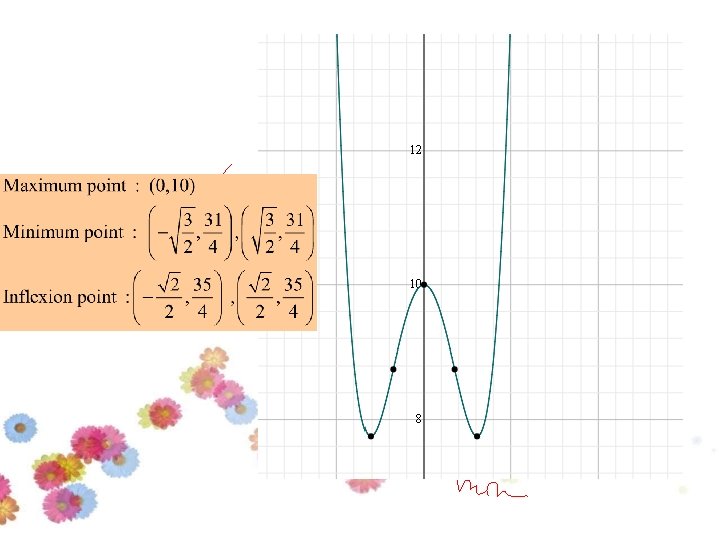
Saddle point : (0, 10) Minimum point : (3, -17) Inflexion point : (0, 10), (2, -6)
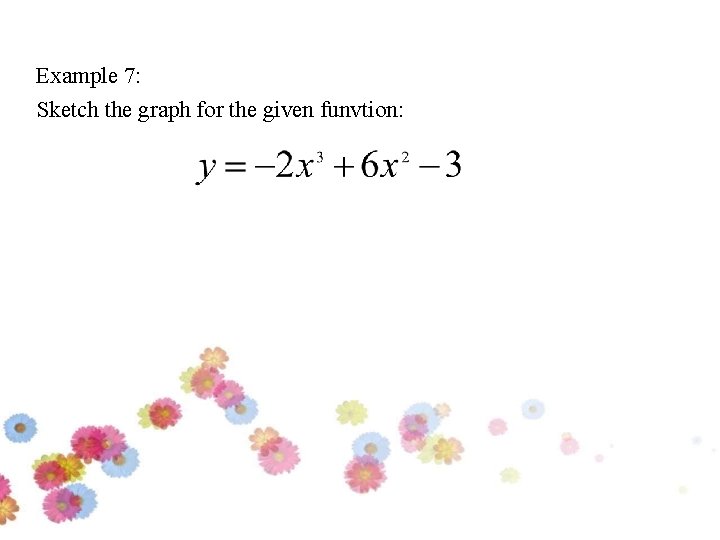
Example 7: Sketch the graph for the given funvtion:

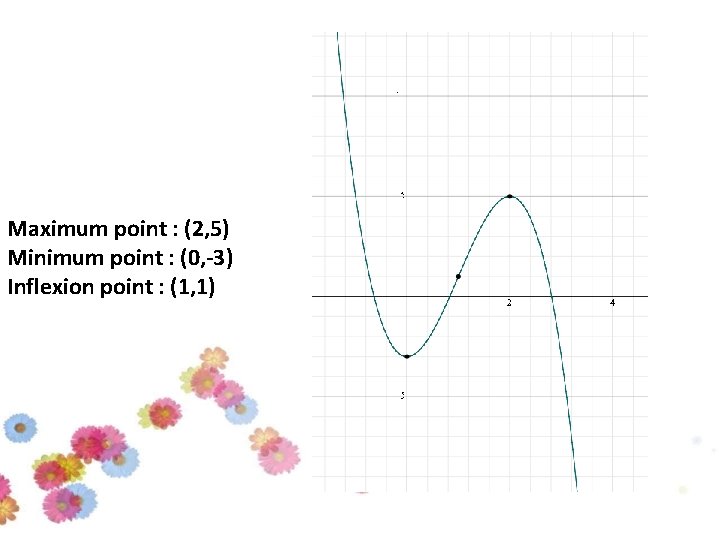
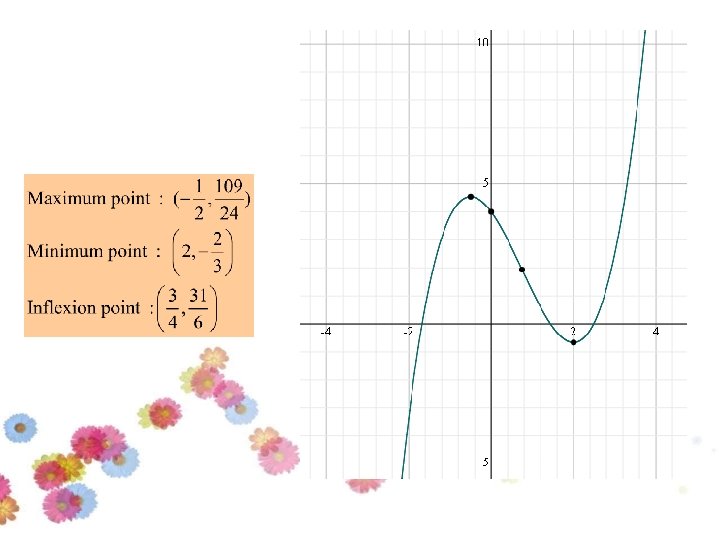
Maximum point : (2, 5) Minimum point : (0, -3) Inflexion point : (1, 1)

Past Exam Questions

Nazuhusna/Microelektronic/UNIMAP 88

Nazuhusna/Microelektronic/UNIMAP 89

Nazuhusna/Microelektronic/UNIMAP 90

Nazuhusna/Microelektronic/UNIMAP 91


Past Exam Questions

 March march dabrowski
March march dabrowski Summary period: march 2021 quiz
Summary period: march 2021 quiz March 5 2021
March 5 2021 Chapter 15 section 4 - aggressors invade nations answer key
Chapter 15 section 4 - aggressors invade nations answer key Chapter 2 differentiation
Chapter 2 differentiation Grihalakshmi magazine march 2019
Grihalakshmi magazine march 2019 Vincent van gogh quotes about death
Vincent van gogh quotes about death Source russia march
Source russia march March 1917 revolution
March 1917 revolution Abraham lincoln
Abraham lincoln Sherman's march significance
Sherman's march significance Path of sherman's march to the sea
Path of sherman's march to the sea Path of sherman's march to the sea
Path of sherman's march to the sea March algorithm
March algorithm American idol
American idol January february march april may
January february march april may Why rizal left london for paris in march 1899?
Why rizal left london for paris in march 1899? January february maruary
January february maruary Sherman's march to the sea
Sherman's march to the sea March 30 1981
March 30 1981 Hemosiderinüri nedir
Hemosiderinüri nedir 20 mile march
20 mile march Glasgow 5th march
Glasgow 5th march Glasgow 5th march 1971
Glasgow 5th march 1971 French revolution women's march
French revolution women's march 535 before 14 march
535 before 14 march Civil war map sherman's march to the sea
Civil war map sherman's march to the sea Military parade commands
Military parade commands Death march edward yourdon
Death march edward yourdon Performance art
Performance art What is the formula for net price
What is the formula for net price Meridel lesueur, new masses, january 1932.
Meridel lesueur, new masses, january 1932. Inurl:bug bounty intext:token of appreciation
Inurl:bug bounty intext:token of appreciation Chinese zodiac march
Chinese zodiac march March madness banner
March madness banner Astronomy picture of the day march 29 2006
Astronomy picture of the day march 29 2006 March algorithm
March algorithm What are the months of fall
What are the months of fall Ce abrasive blasting respirator
Ce abrasive blasting respirator March 1 1803
March 1 1803 March joint powers authority
March joint powers authority 21 march equinox
21 march equinox The deguello is the traditional march of no
The deguello is the traditional march of no Sousa march mania
Sousa march mania Happy wednesday march
Happy wednesday march March 7, 2012
March 7, 2012 March 7 2008
March 7 2008 Globalisation of western childhood
Globalisation of western childhood Ides of march punic wars
Ides of march punic wars Churchill iron curtain cartoon
Churchill iron curtain cartoon Ausias march poema xiii
Ausias march poema xiii Syntax pronunciation
Syntax pronunciation Writing to learn
Writing to learn March 2 success.com
March 2 success.com What is ngo?
What is ngo? Offset printing march
Offset printing march What did st patrick chase out of ireland
What did st patrick chase out of ireland Slice march
Slice march March madness dataset
March madness dataset Transpiration practical grade 10
Transpiration practical grade 10 Geogrphic
Geogrphic Salt march
Salt march 25 march 2008
25 march 2008 Deficiency of
Deficiency of Entertainment identifier registry
Entertainment identifier registry Death march edward yourdon
Death march edward yourdon March 22 2010
March 22 2010 1965 march
1965 march March 25 2011
March 25 2011 Ano ang rebelyong boxer
Ano ang rebelyong boxer Albert einstein
Albert einstein Someone is taking someone for a walk cartoon analysis
Someone is taking someone for a walk cartoon analysis Royal march banner
Royal march banner The annunciation march 25
The annunciation march 25 Critical essay format
Critical essay format Sigma lean sgrho
Sigma lean sgrho Not just bingo march
Not just bingo march National 5 critical essay example
National 5 critical essay example March kindergarten newsletter
March kindergarten newsletter May june july
May june july 23 march 1996
23 march 1996 Why is the long march important
Why is the long march important March 23 world meteorological day
March 23 world meteorological day Easter is a joyful festival which happens
Easter is a joyful festival which happens Jan feb mar
Jan feb mar Jan rose kasmir
Jan rose kasmir Wasserstand bernhardsthal
Wasserstand bernhardsthal Poem for 8 march
Poem for 8 march Joyful mysteries
Joyful mysteries March 14 445 bc
March 14 445 bc Macro environnement marketing
Macro environnement marketing March
March Language objective differentiation for proficiency levels
Language objective differentiation for proficiency levels Difference between udl and differentiation
Difference between udl and differentiation High accuracy differentiation formulas
High accuracy differentiation formulas