Chapter 4 continued Download this file V Conditional

Chapter 4, continued. . . Download this file.

V. Conditional Probabilities Notation: P(A B) Conditional probabilities calculate the probability of event A, given that event B has already occurred. For example, it would consider the probability of a customer purchasing a new car, given that we know the customer is female. This may indeed be different than simply estimating the probability that any one customer will purchase the new car.

A. Conditional Calculation General formula for a conditional probability : P(A B) In other words, a conditional probability is the ratio of a joint probability to a marginal probability.

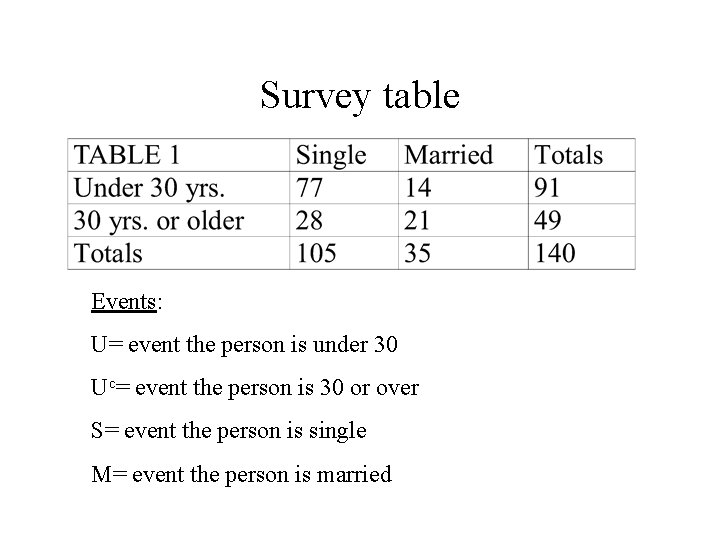
An example. Problem 44 in the text. Owners of a Daytona Beach nightclub survey 140 customers to gather information about their age and marital status. This information is summarized in the following table.

Survey table Events: U= event the person is under 30 Uc= event the person is 30 or over S= event the person is single M= event the person is married

Joint Probabilities • P(A B) is the probability of both events occurring. • For example, there are 77 people who are both single and under 30. P(U S)=77/140=. 55 • Calculate the following joint probabilities: P(U M)= P(Uc S)= P(Uc M)=

Marginal Probabilities • This is simply the probability of observing just one event. • For example, there are 91 people who are under 30. P(U)=91/140=. 65 • Calculate the following marginal probabilities: P(M)= P(Uc)= P(S)=

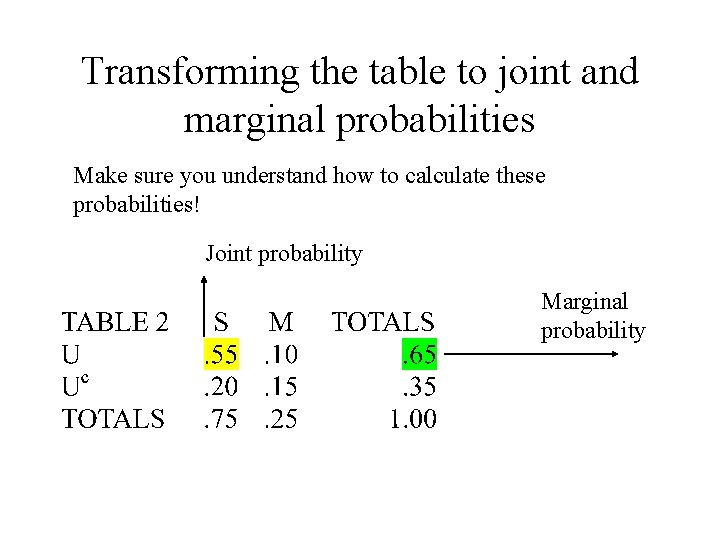
Transforming the table to joint and marginal probabilities Make sure you understand how to calculate these probabilities! Joint probability Marginal probability

Finding the conditional probabilities Recall our formula: P(A B) Thus P(U|S)=P(U S)/P(S) = (77/140)/(105/140) =77/105=. 733 Calculate the remaining conditional probabilities. If you’re confused, bring a specific question(s) to class.