Chapter 4 Classical Methods in Techniques of Analytical

Chapter 4 : Classical Methods in Techniques of Analytical Chemistry : Titrimetric Methods of Analysis Pn Syazni Zainul Kamal PPK Bioproses

n CO 4: ABILITY TO DIFFERENTIATE AND CALCULATE CONCENTRATION OF ANALYTES OF VARIOUS TITRIMETRIC METHODS (ACID-BASE, COMPLEXATION, REDOX, PRECIPITATION)

What is Titrimetry? ? Any method in which volume is the signal. Also known as volumetric method. n

Types of Titrimetric Methods - 1. 2. 3. 4. Classified into four groups based on type of reaction involve; Acid-base titrations Complexometric titrations Redox titrations Precipitation titrations

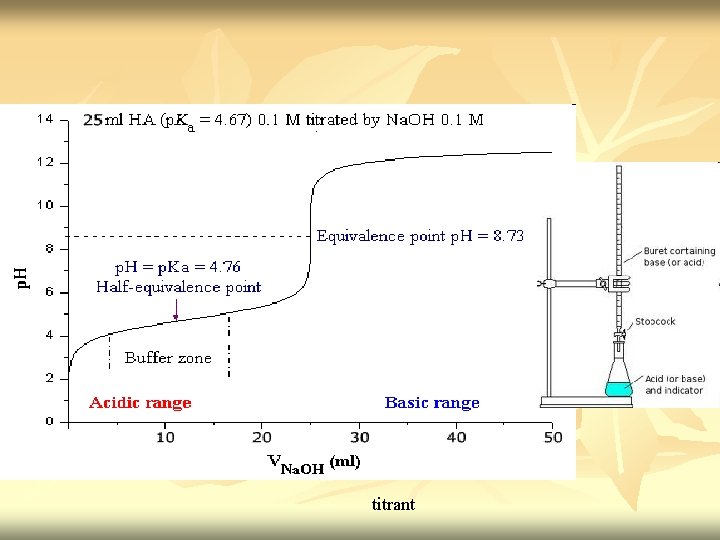
Acid base titration n n Neutralization - acid reacted with equivalent amount of base Titration curve – the independent variable (X) is the volume of the titrant, while the dependent variable (Y) is the p. H of the solution (which changes depending on the composition of the two solutions). Titrant: A reagent of a known concentration Equivalence point: the point at which all of the starting solution, eg an acid, has been neutralized by the titrant, eg a base.

titrant

n End point/ equivalence point – signals the completion of the reaction (the point at which all of the starting solution, usually an acid, has been neutralized by the titrant, usually a base).

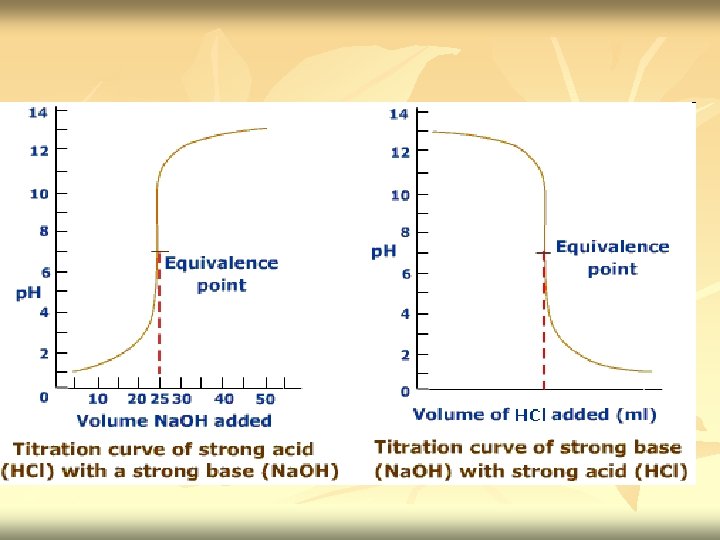
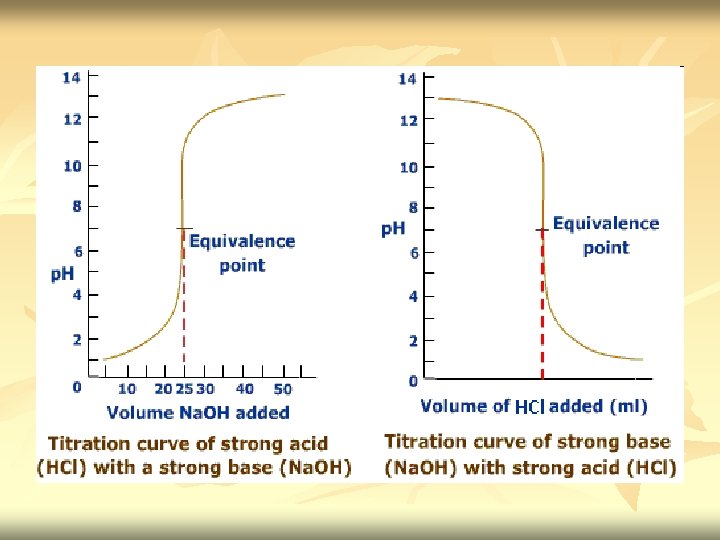
Strong acid vs strong base (easy titration)

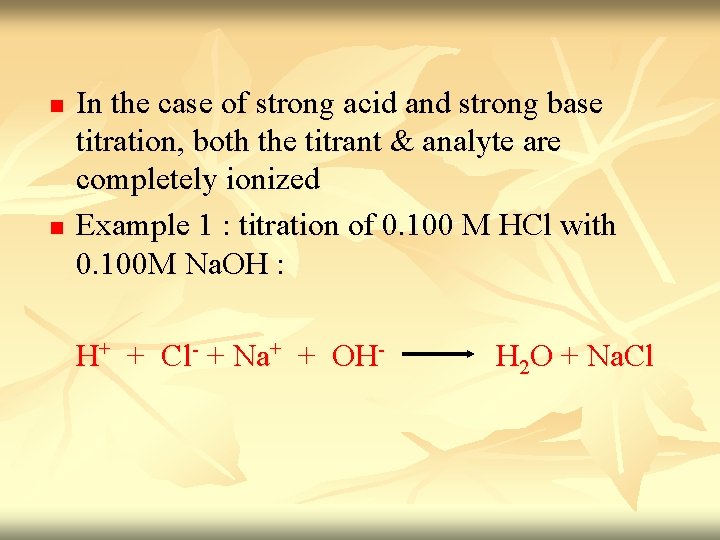
n n In the case of strong acid and strong base titration, both the titrant & analyte are completely ionized Example 1 : titration of 0. 100 M HCl with 0. 100 M Na. OH : H+ + Cl- + Na+ + OH- H 2 O + Na. Cl

n n Before titration started – only have HCl. [H+]=[HX] Titration proceed – part of H+ is removed from solution as H 2 O. [H+] decrease gradually. p. H increase [H+]=[remaining HX] At equivalence point - we have solution of Na. Cl. Neutralization complete. HCl had been neutralize by Na. OH. [H+]= √Kw Excess Na. OH added – [OH-] increase. p. H is determine by concentration of OH[OH-]=[excess titrant]

Equation governing a strong acid (HX) titration Fraction F titrated Present Equation F=0 HX [H+]=[HX] 0<F<1 HX/X- [H+]=[remaining. HX] F=1 X- [H+]= √Kw F>1 OH-/X- [OH-]=[excess titrant]

n A 50. 0 ml aliquot of 0. 100 M HCl is titrated with 0. 200 M Na. OH. Calculate the p. H of the solution after addition of 0. 0, 5. 0, 10. 0, 25. 0, 35. 0, 45. 0, 55. 0 of Na. OH Molarity = total moles of solute (mol)/vol. of solution (ml)

Solution : a) Addition 0 f 0. 0 ml Na. OH [H+]=[HX] p. H = - log [H+] = - log 0. 100 = 1. 00

b) Addition of 5. 0 ml Na. OH [H+]=[remaining HX] Initial mmol H+ = 0. 100 M x 50. 0 ml = 5. 00 mmol OH- added = 0. 200 M x 5. 0 ml = 1. 00 mmol H+ left = 4. 00 mmol in 55. 0 ml [H+] = 4. 00 mmol = 0. 0727 M (5. 0 + 50. 0)ml p. H = - log [H+] = - log 0. 0727 = 1. 14

c) Addition of 25. 0 ml Na. OH Initial mmol H+ = 0. 100 M x 50. 0 ml = 5. 00 mmol OH- added = 0. 200 M x 25. 0 ml = 5. 00 mmol The equivalence point is reached. All H+ had reacted with OH-. The H+ now is from H 2 O. Na. Cl does not contribute to any p. H value. [H+]= √Kw = √ 1. 00 x 10 -14 = 1. 00 x 10 -7 p. H = - log 1. 00 x 10 -7 = 7. 00

c) Addition of 35 ml Na. OH Initial mmol H+ = 0. 100 M x 50. 0 ml = 5. 00 mmol OH- added = 0. 200 M x 35. 0 ml = 7. 00 mmol OH- excess 2. 0 mmol [OH-]=[excess titrant] [OH+] = 2. 0 mmol = 0. 0235 M [OH+] (35. 0 + 50. 0)ml p. OH = - log [OH+] = - log 0. 0235 = 1. 63 p. OH p. H = 14. 00 – 1. 63 = 12. 37

STRONG BASE VERSUS STRONG ACID

Equation governing a strong base (BOH) titration Fraction F titrated Present Equation F=0 BOH [OH-]=[BOH] 0<F<1 BOH/B+ [OH-]=[remaining. BOH] F=1 B+ [H+]= √Kw F>1 H+/B+ [H+]=[excess titrant]

Question 1 n A 50. 0 ml aliquot of 0. 100 M Na. OH is titrated with 0. 200 M HCl. Calculate the p. H of the solution after addition of 0. 0, 5. 0, 10. 0, 25. 0, 35. 0, 45. 0, 55. 0 of HCl. Plot the titration curve in a graph paper.

WEAK ACID VERSUS STRONG BASE

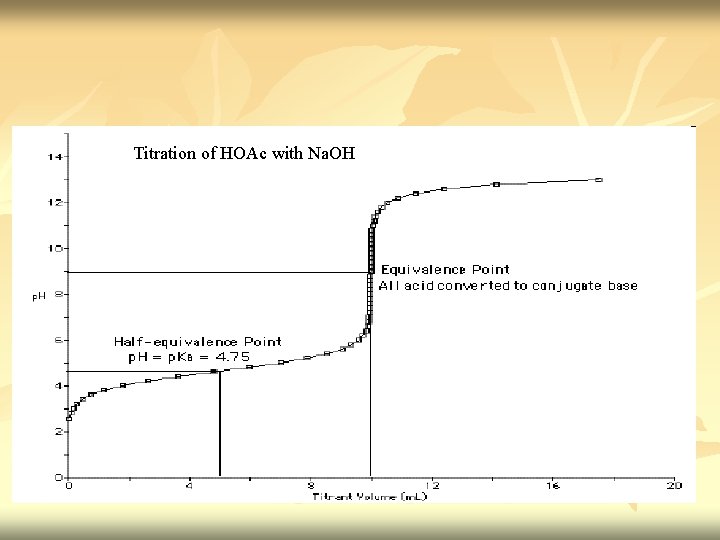
Weak acid Vs Strong base n n n Titration of 100 ml 0. 1 M acetic acid with 0. 1 M sodium hydroxide Neutralization reaction : HOAc + Na+ + OH- H 2 O + Na+ + OAc. Acetic acid is neutralized to water and equivalent amount of sodium acetate.

n n Before titration started – only have HOAc. [H+]= √Ka. CHA Titration started - some of HOAc convert to Na. OAc & buffer system set up. Titration proceed – p. H increase slowly as the ratio [OAc-]/[HOAc] change. p. H=p. Ka + log CA CHA Midpoint of titration – [OAc-] = [HOAc] (p. H=p. Ka)

n At equivalence point – we have solution of Na. OAc is a bronsted base (it hydrolyze in water to form OH- and undissociate HOAc) [OH-]=√Kw. CA- n Ka Excess Na. OH added – p. H is determine by concentration of OH-

Titration of HOAc with Na. OH

Equation governing a weak-acid (HA) Fraction F titrated Present Equation F=0 HA [H+]= √Ka. CHA 0<F<1 HA/A- p. H=p. Ka + log CA CHA F=1 A- [OH-]=√Kw. CA Ka F>1 OH-/A- [OH-]= [excess titrant]

Exercise 1 A 50. 0 ml aliquot of 0. 100 M acetic acid is titrated with 0. 100 M Na. OH. Calculate the p. H of the solution after the addition of 0. 0, 5. 0, 25. 0, 45. 0, 50. 0, 55. 0 and 75. 0 ml of Na. OH. The dissociation constant for acetic acid is 1. 75 x 10 -5

Solution a) Addition of 0. 0 ml Na. OH At 0 ml, we have a solution of only 0. 100 M HOAc: HOAc H+ + OAc. Initial (M) 0. 100 0 Equilibrium (M) 0. 100 – x x [H+][OAc-] = (x)(x) = 1. 75 x 10 -5 [HOAc] 0. 100 x = [H+] = 1. 32 x 10 -3 M p. H = - log 1. 32 x 10 -3 M = 2. 88

b) Addition of 5. 0 ml Na. OH Initial mmol HOAc = 50. 0 ml x 0. 100 M =5. 00 mmol Na. OH added = 5. 0 ml x 0. 100 M =0. 50 mmol =mmol OAc- form mmol HOAc left =4. 50 mmol p. H=p. Ka + log CA CHA = - log 1. 75 x 10 -5 + log 0. 50 = 3. 81 4. 50

c) Addition of 50. 0 ml Na. OH Initial mmol HOAc = 50. 0 ml x 0. 100 M =5. 00 mmol Na. OH added = 50. 0 ml x 0. 100 M =5. 00 mmol Equivalence point is reached. The solution contain salt of weak acid (conjugate base), Na. OAc, hence the hydrolysis of salt will take place. All HOAc has been converted to OAc - (5. 00 mmol in 100 ml or 0. 0500 M) Na. OAc Na+ + OAc- + H 2 O HOAc + OH- [OH-]=√Kw. CA Ka =√ 1. 00 x 10 -14 x 0. 0500 = 5. 35 x 10 -6 1. 75 x 10 -5 p. OH = -log 5. 35 x 10 -6 = 5. 27 p. H = 14. 00 – 5. 27 = 8. 72

d) Addition of 55. 0 ml Na. OH Initial mmol HOAc = 50. 0 ml x 0. 100 M =5. 00 mmol Na. OH added = 55. 0 ml x 0. 100 M =5. 50 mmol Excess OH- =0. 50 mmol in 105 ml At 55. 0 ml, we have solution of Na. OAc and excess added Na. OH. So p. H is calculated by concentration of excess OH-. [OH-] = 0. 50 mmol = 4. 76 x 10 -3 (50+55)ml p. OH = - log [OH-] = - log 4. 76 x 10 -3 = 2. 32 p. H = 14. 00 – 2. 32 = 11. 68

WEAK BASE VERSUS STRONG ACID

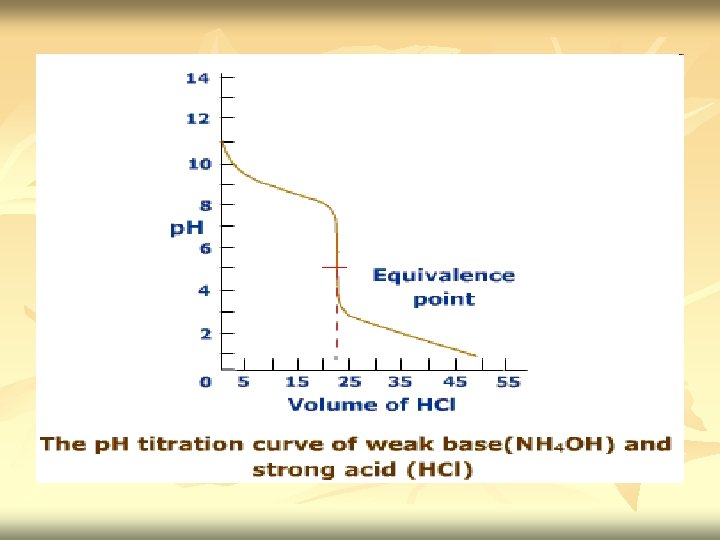
Weak base vs strong acid n n Titration curve reverse of those for a weak acid versus strong base Titration of 100 ml 0. 1 M ammonia with 0. 1 M HCl NH 3 + H+ + Cl- NH 4+ + Cl-

n n Before titration started – only have 0. 1 M NH 3. [OH+]= √Kb. Cb Titration started - some of NH 3 convert to NH 4+ & buffer system set up. Titration proceed – p. H decrease slowly as the ratio [NH 3]/[NH 4+] change. p. H=(p. Kw – p. Kb) + log CB CBH+ Midpoint of titration – [NH 4+] = [NH 3] (p. H=14 - p. Kb)

n n At equivalence point – we have solution of NH 4 Cl. Neutralization complete. NH 3 had been neutralize by HCl. [H+]=√Kw. CBH+ Kb Excess Na. OH added – p. H is determine by concentration of H+

Assignment 1 Question 2 n Sketch a titration curve based on the p. H values calculated from the addition of 0. 0, 10. 0, 25. 0, 40. 0, 55. 0 and 60. 0 ml of 0. 100 M HCl into 50. 0 ml 0. 100 M NH 3. Kb is 1. 75 x 10 -5. n Submit on :

Titration of polyprotic acid Monoprotic acids n Monoprotic acids are those acids that are able to donate one proton per molecule during the process of dissociation (ionization): n HA(aq) + H 2 O(l) H 3 O+(aq) + A−(aq) Ka

Polyprotic acids n Polyprotic acids are able to donate more than one proton per acid molecule, in contrast to monoprotic acids that only donate one proton per molecule. n diprotic acid (two potential protons to donate) and triprotic acid (three potential protons to donate).

n n A diprotic acid (H 2 A) can undergo one or two dissociations depending on the p. H. Each dissociation has its own dissociation constant, Ka 1 and Ka 2. H 2 A(aq) + H 2 O(l) H 3 O+(aq) + HA−(aq) Ka 1 HA−(aq) + H 2 O(l) H 3 O+(aq) + A 2−(aq) Ka 2

Assingment 1 n Question 2 A 50 ml solution of 0. 100 M H 2 M is titrated with 0. 100 M Na. OH. Calculate the p. H after adding 0. 0, 10. 0, 25. 0, 45. 0, 50. 0, 75. 0, 95. 0, 100. 0 and 110 ml of Na. OH. Sketch a titration curve from the calculated p. H values. For H 2 M, Ka 1 = 1. 0 x 10 -3 and Ka 2 = 1. 0 x 10 -7