Chapter 4 Circuit Theorems SJTU 1 Linearity Property

Chapter 4 Circuit Theorems SJTU 1

Linearity Property • Linearity is the property of an element describing a linear relationship between cause and effect. • A linear circuit is one whose output is linearly ( or directly proportional) to its input. SJTU 2

Fig. 4. 4 For Example 4. 2 SJTU 3

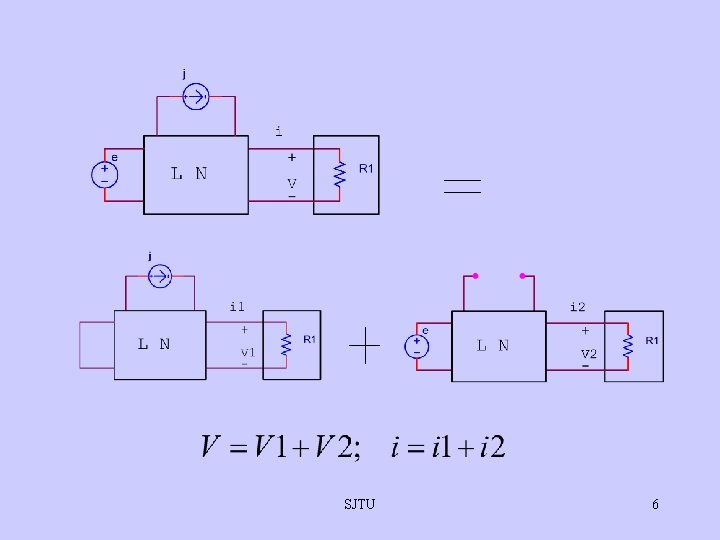
Superposition(1) • The superposition principle states that voltage across (or current through) an element in a linear circuit is the algebraic sum of the voltages across (or currents through) that element due to each independent source acting alone. SJTU 4

Superposition(2) • Steps to Apply Superposition Principle: 1. Turn off all independent source except one source. Find the output(voltage or current) due to that active source using nodal or mesh analysis. Repeat step 1 for each of the other independent sources. Find the total contribution by adding algebraically all the contributions due to the independent sources. 2. 3. SJTU 5

SJTU 6

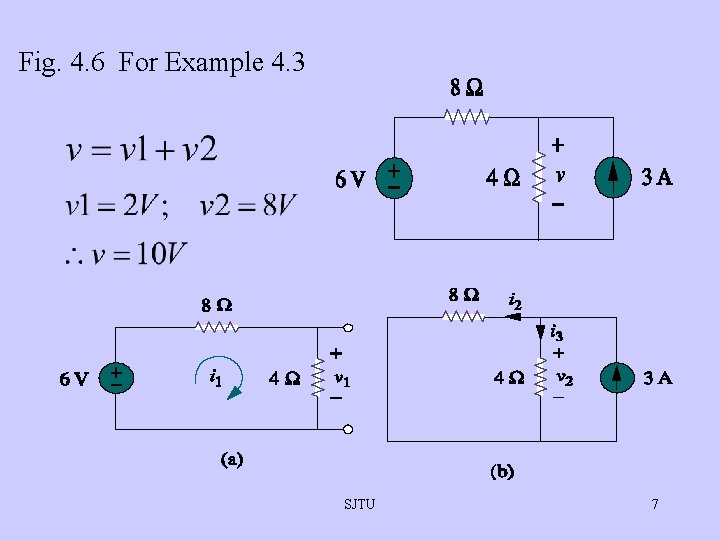
Fig. 4. 6 For Example 4. 3 SJTU 7

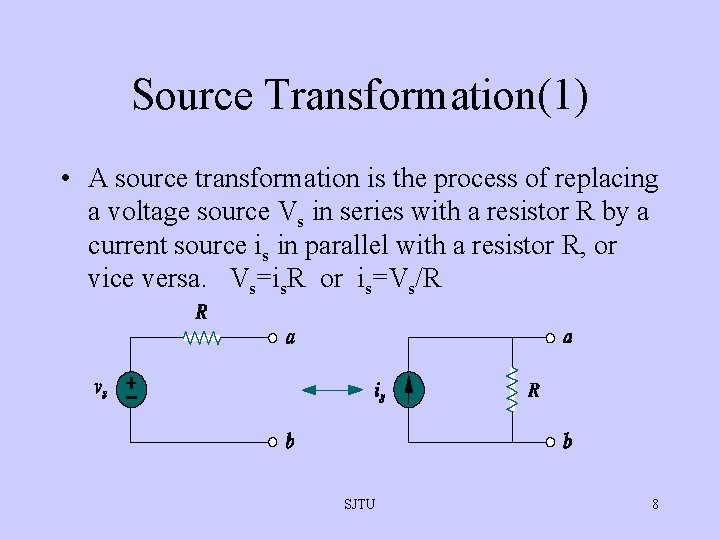
Source Transformation(1) • A source transformation is the process of replacing a voltage source Vs in series with a resistor R by a current source is in parallel with a resistor R, or vice versa. Vs=is. R or is=Vs/R SJTU 8

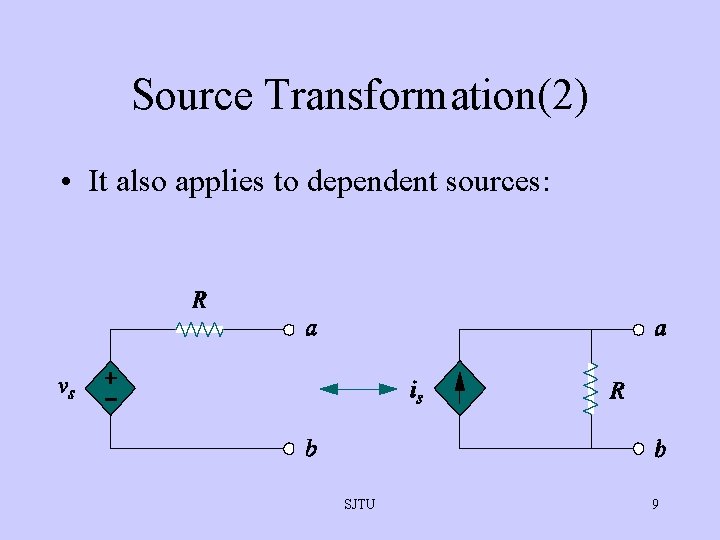
Source Transformation(2) • It also applies to dependent sources: SJTU 9

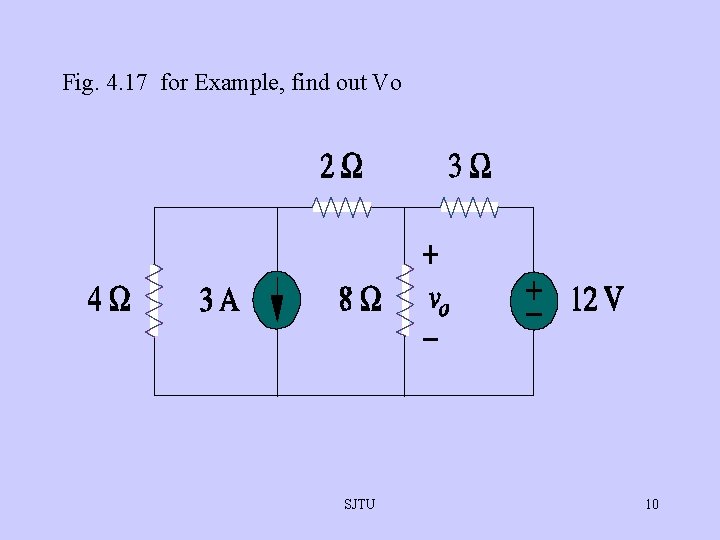
Fig. 4. 17 for Example, find out Vo SJTU 10

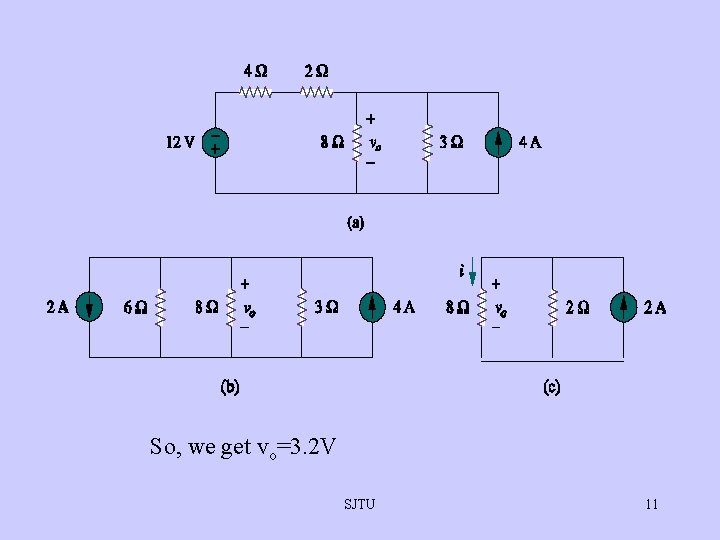
So, we get vo=3. 2 V SJTU 11

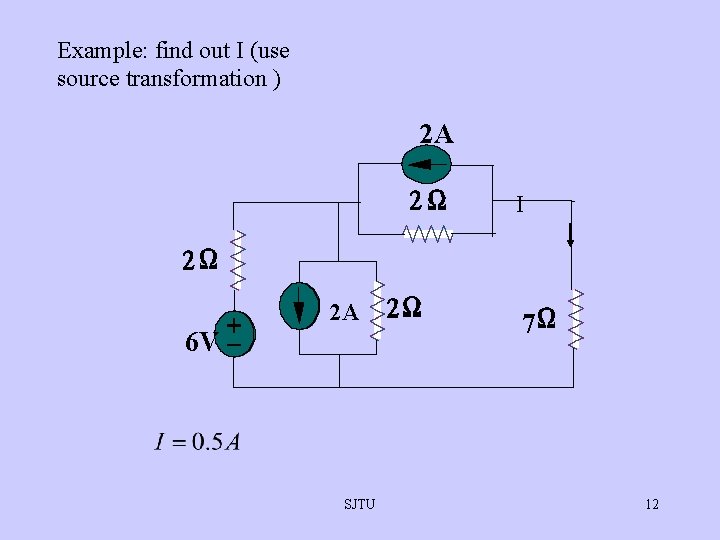
Example: find out I (use source transformation ) 2 A I 2 A 6 V SJTU 7 12

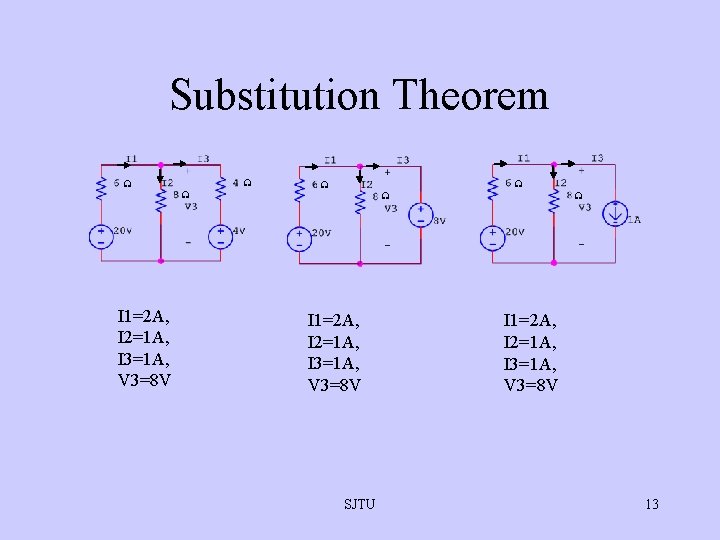
Substitution Theorem I 1=2 A, I 2=1 A, I 3=1 A, V 3=8 V SJTU I 1=2 A, I 2=1 A, I 3=1 A, V 3=8 V 13

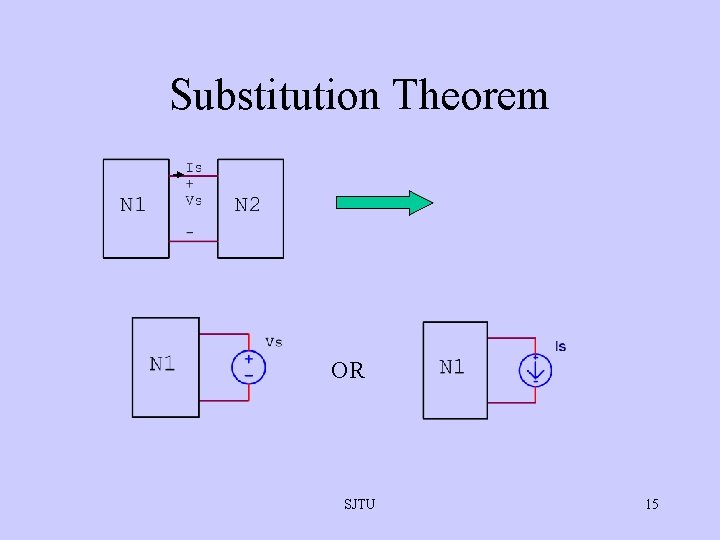
Substitution Theorem • If the voltage across and current through any branch of a dc bilateral network are known, this branch can be replaced by any combination of elements that will maintain the same voltage across and current through the chosen branch. SJTU 14

Substitution Theorem OR SJTU 15

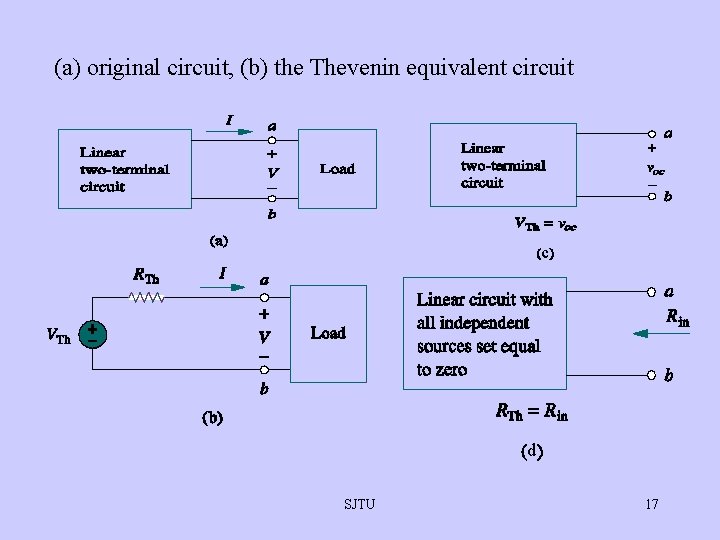
Thevenin’s Theorem • A linear two-terminal circuit can be replaced by an equivalent circuit consisting of a voltage source Vth in series with a resistor Rth, where Vth is the open-circuit voltage at the terminals and Rth is the input or equivalent resistance at the terminals when the independent source are turned off. SJTU 16

(a) original circuit, (b) the Thevenin equivalent circuit c d SJTU 17

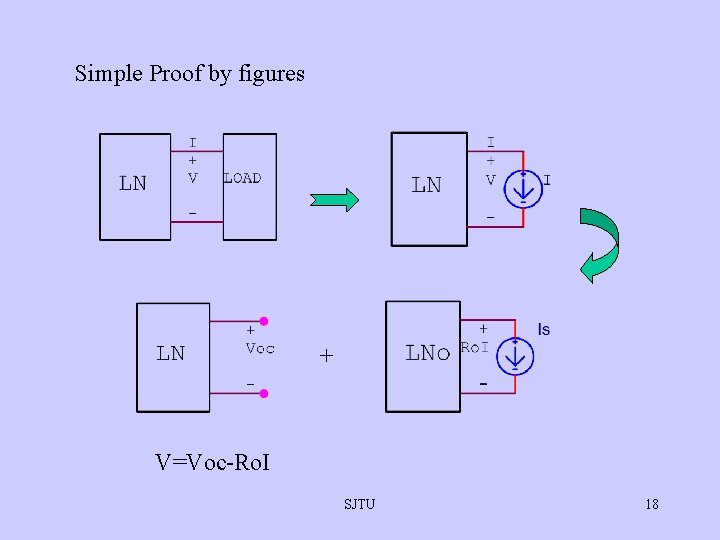
Simple Proof by figures + V=Voc-Ro. I SJTU 18

Thevenin’s Theorem Consider 2 cases in finding Rth: • Case 1 If the network has no dependent sources, just turn off all independent sources, calculate the equivalent resistance of those resistors left. • Case 2 If the network has dependent sources, there are two methods to get Rth: 1. SJTU 19

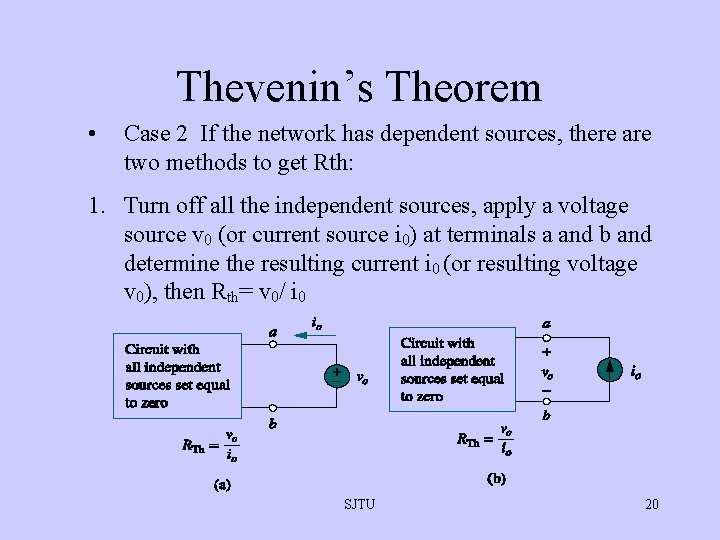
Thevenin’s Theorem • Case 2 If the network has dependent sources, there are two methods to get Rth: 1. Turn off all the independent sources, apply a voltage source v 0 (or current source i 0) at terminals a and b and determine the resulting current i 0 (or resulting voltage v 0), then Rth= v 0/ i 0 SJTU 20

Thevenin’s Theorem • 2. Case 2 If the network has dependent sources, there are two methods to get Rth: Calculate the open-circuit voltage Voc and short-circuit current Isc at the terminal of the original circuit, then Rth=Voc/Isc SJTU 21

Examples SJTU 22

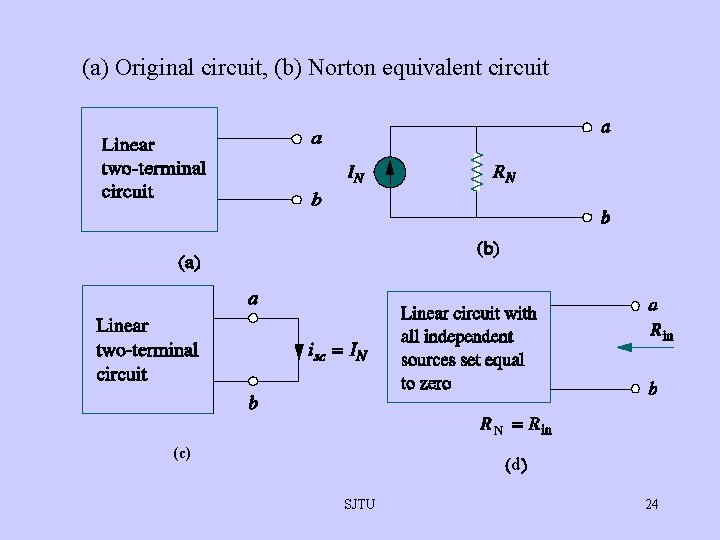
Norton’s Theorem • A linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source IN in parallel with a resistor RN, where IN is the short-circuit current through the terminals and RN is the input or equivalent resistance at the terminals when the independent sources are turned off. SJTU 23

(a) Original circuit, (b) Norton equivalent circuit N (c) d SJTU 24

Examples SJTU 25

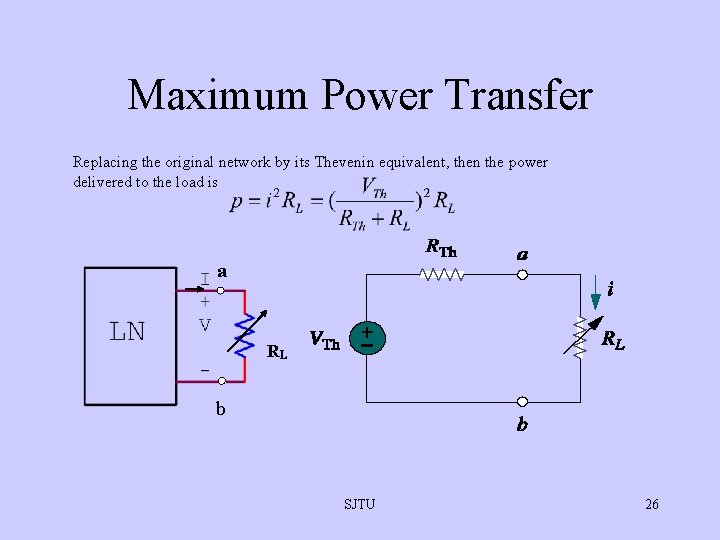
Maximum Power Transfer Replacing the original network by its Thevenin equivalent, then the power delivered to the load is a RL b SJTU 26

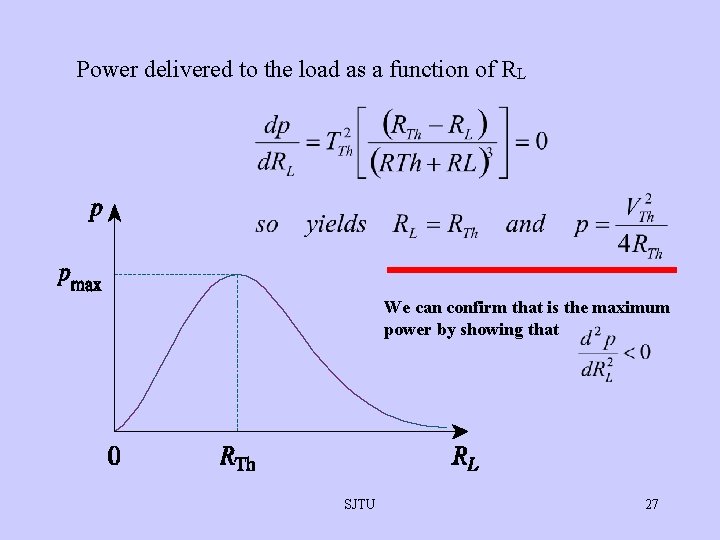
Power delivered to the load as a function of RL We can confirm that is the maximum power by showing that SJTU 27

Maximum Power Transfer (several questions) • If the load RL is invariable, and RTh is variable, then what should RTh be to make RL get maximum power? • If using Norton equivalent to replace the original circuit, under what condition does the maximum transfer occur? • Is it true that the efficiency of the power transfer is always 50% when the maximum power transfer occurs? SJTU 28

Examples SJTU 29

Tellegen Theorem • If there are b branches in a lumped circuit, and the voltage uk, current ik of each branch apply passive sign convention, then we have SJTU 30

Inference of Tellegen Theorem • If two lumped circuits and have the same topological graph with b branches, and the voltage, current of each branch apply passive sign convention, then we have not only SJTU 31

Example SJTU 32

Reciprocity Theorem 2 6 2 3 SJTU 6 3 33

Reciprocity Theorem (only applicable to reciprocity networks) • Case 1 The current in any branch of a network, due to a single voltage source E anywhere else in the network, will equal the current through the branch in which the source was originally located if the source is placed in the branch in which the current I was originally measured. SJTU 34

Reciprocity Theorem (only applicable to reciprocity networks) Case 2 SJTU 35

Reciprocity Theorem (only applicable to reciprocity networks) Case 3 SJTU 36

example SJTU 37

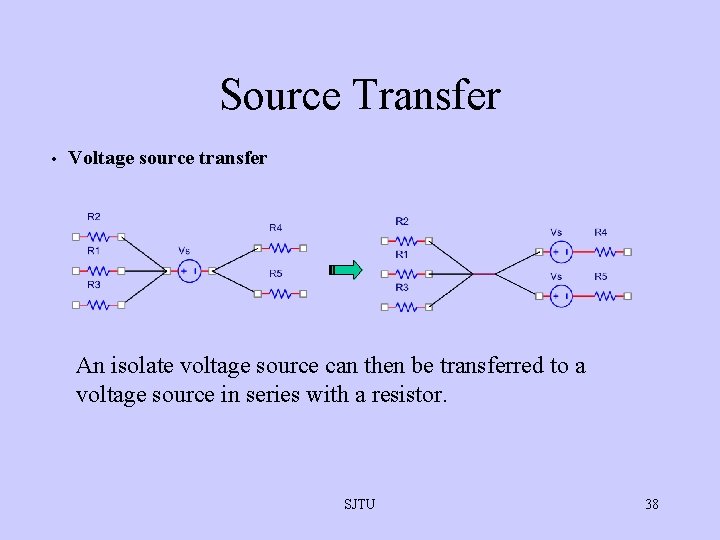
Source Transfer • Voltage source transfer An isolate voltage source can then be transferred to a voltage source in series with a resistor. SJTU 38

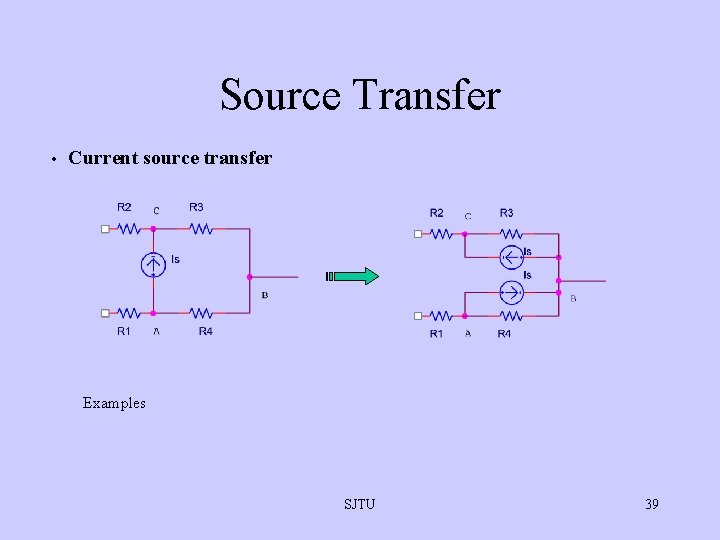
Source Transfer • Current source transfer Examples SJTU 39

Summary • • • Linearity Property Superposition Source Transformation Substitution Theorem Thevenin’s Theorem Norton’s Theorem • Maximum Power Transfer • Tellegen Theorem • Inference of Tellegen Theorem • Reciprocity Theorem • Source Transfer SJTU 40