Chapter 4 Channel Coding and Error Control Copyright

Chapter 4 Channel Coding and Error Control Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 1

Outline n n n n n Introduction Block Codes Cyclic Codes CRC (Cyclic Redundancy Check) Convolutional Codes Interleaving Information Capacity Theorem Turbo Codes ARQ (Automatic Repeat Request) n n n Stop-and-wait ARQ Go-back-N ARQ Selective-repeat ARQ Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 2

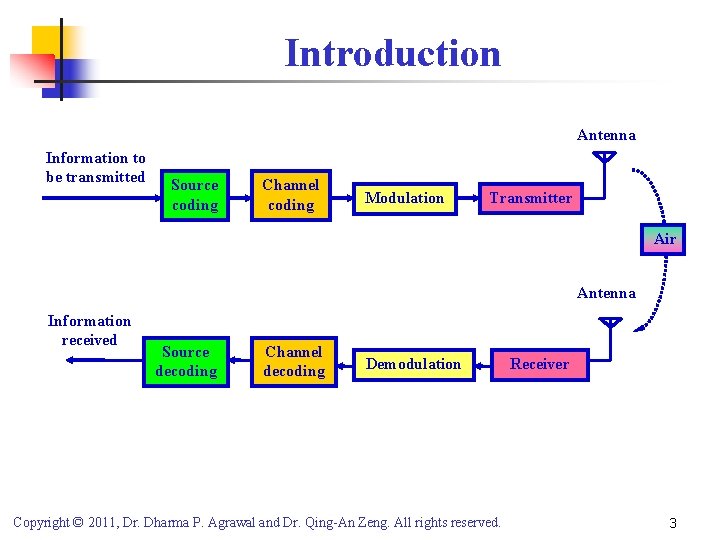
Introduction Antenna Information to be transmitted Source coding Channel coding Modulation Transmitter Air Antenna Information received Source decoding Channel decoding Demodulation Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. Receiver 3

Forward Error Correction (FEC) n n The key idea of FEC is to transmit enough redundant data to allow receiver to recover from errors all by itself. No sender retransmission required The major categories of FEC codes are n n n Block codes Cyclic codes Reed-Solomon codes (Not covered here) Convolutional codes, and Turbo codes, etc. Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 4

Linear Block Codes n n n Information is divided into blocks of length k r parity bits or check bits are added to each block (total length n = k + r) Code rate R = k/n Decoder looks for codeword closest to received vector (code vector + error vector) Tradeoffs between n n Efficiency Reliability Encoding/Decoding complexity Modulo 2 Addition Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 5

Linear Block Codes: Example : Find linear block code encoder G if code generator polynomial g(x)=1+x+x 3 for a (7, 4) code; n = Total number of bits = 7, k = Number of information bits = 4, r = Number of parity bits = n - k = 3 I is the identity matrix P is the parity matrix Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 6

Linear Block Codes: Example The Generator Polynomial can be used to determine the Generator Matrix G that allows determination of parity bits for a given data bits of m by multiplying as follows: Data Parity Can be done for other combination of data bits, giving the code word c Other combinations of m can be used to determine all other possible code words Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 7

Linear Block Codes K- data and r=n-k redundant bits Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 8

Linear Block Codes The uncoded k data bits be represented by the m vector: m=(m 1, m 2, …, mk) The corresponding codeword be represented by the nbit c vector: c=(c 1, c 2, …ck, ck+1, …, cn-1, cn) n Each parity bit consists of weighted modulo 2 sum of the data bits represented by symbol for Exclusive OR or modulo 2 -addition n Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 9

Linear Block Codes § Linear Block Code The block length C of the Linear Block Code is C=m. G where m is the information codeword block length, G is the generator matrix. G = [Ik | P]k × n where Pi = Remainder of [xn-k+i-1/g(x)] for i=1, 2, . . , k, and I is unit or identity matrix. § At the receiving end, parity check matrix can be given as: H = [PT | In-k ], where PT is the transpose of the matrix p. Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 10

Linear Block Codes Example : Find linear block code encoder G if code generator polynomial g(x) with k data bits, and r parity bits = n - k where Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 11

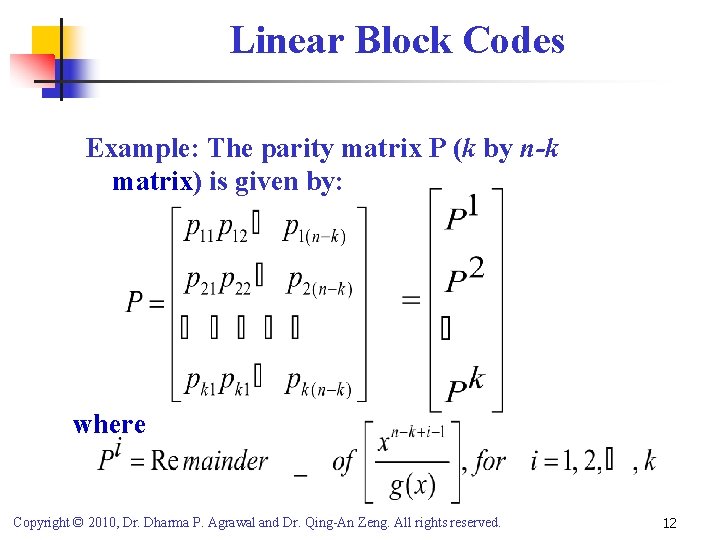
Linear Block Codes Example: The parity matrix P (k by n-k matrix) is given by: where Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 12

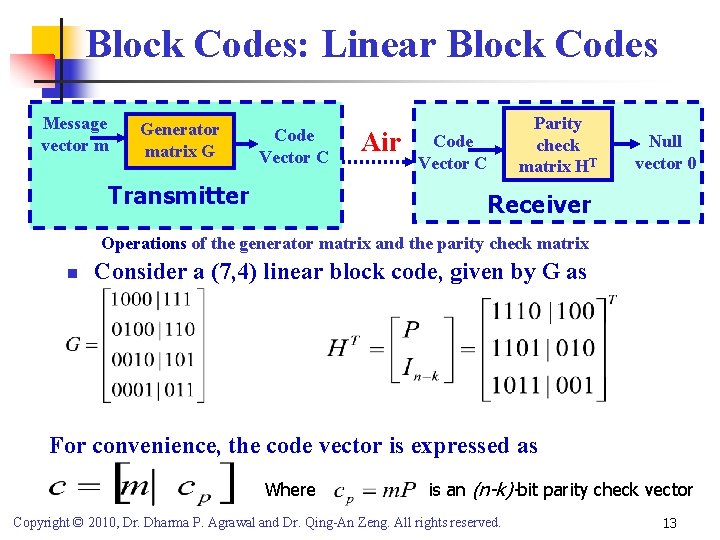
Block Codes: Linear Block Codes Message vector m Generator matrix G Code Vector C Transmitter Air Code Vector C Parity check matrix HT Null vector 0 Receiver Operations of the generator matrix and the parity check matrix n Consider a (7, 4) linear block code, given by G as For convenience, the code vector is expressed as Where is an (n-k)-bit parity check vector Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 13

Block Codes: Linear Block Codes Define matrix HT as Received code vector x = c e, here e is an error vector, the matrix HT has the property The transpose of matrix HT is Where In-k is a n-k by n-k unit matrix and PT is the transpose of parity matrix P. H is called parity check matrix. Compute syndrome as s = x HT =( c e ) * HT =c HT e HT = e HT Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 14

Linear Block Codes If S is 0 then message is correct else there are errors in it, from common known error patterns the correct message can be decoded. n For the (7, 4) linear block code, given by G as n For m = [1 0 1 1] and c = m. G = [1 0 1 1| 0 0 1] If there is no error, the received vector x=c, and s=c. HT=[0, 0, 0] Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 15

Linear Block Codes Let c suffer an error such that the received vector x=c e =[ 1 0 1 1 0 0 1 ] [ 0 0 1 0 0 ] =[ 1 0 0 1 ] Then, Syndrome s=x. HT This indicates error position, giving the corrected vector as [1011001] Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 16

Cyclic Codes It is a block code which uses a shift register to perform encoding and decoding the code word with n bits is expressed as: c(x)=c 1 xn-1 +c 2 xn-2……+ cn where each coefficient ci (i=1, 2, . . , n) is either a 1 or 0 The codeword can be expressed by the data polynomial m(x) and the check polynomial cp(x) as c(x) = m(x) xn-k + cp(x) where cp(x) = remainder from dividing m(x) xn-k by generator g(x) if the received signal is c(x) + e(x) where e(x) is the error To check if received signal is error free, the remainder from dividing c(x) + e(x) by g(x) is obtained(syndrome). If this is 0 then the received signal is considered error free else error pattern is detected from known error syndromes Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 17

Cyclic Code: Example : Find the codewords c(x) if m(x)=1+x+x 2 and g(x)=1+x+x 3 for (7, 4) cyclic code We have n = Total number of bits = 7, k = Number of information bits = 4, r = Number of parity bits = n - k = 3 Then, Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 18

Cyclic Redundancy Check (CRC) n n n Cyclic redundancy Code (CRC) is an error-checking code The transmitter appends an extra n-bit sequence to every frame called Frame Check Sequence (FCS). The FCS holds redundant information about the frame that helps the receivers detect errors in the frame CRC is based on polynomial manipulation using modulo arithmetic. Blocks of input bit as coefficient-sets for polynomials is called message polynomial. Polynomial with constant coefficients is called the generator polynomial Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 19

Cyclic Redundancy Check (CRC) n n Generator polynomial is divided into the message polynomial, giving quotient and remainder, the coefficients of the remainder form the bits of final CRC Define: Q – The original frame (k bits) to be transmitted F – The resulting frame check sequence (FCS) of n-k bits to be added to Q (usually n=8, 16, 32) J – The cascading of Q and F P – The predefined CRC generating polynomial The main idea in CRC algorithm is that the FCS is generated so that J should be exactly divisible by P Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 20

Cyclic Redundancy Check (CRC) n n The CRC creation process is defined as follows: n Get the block of raw message n Left shift the raw message by n bits and then divide it by p n Get the remainder R as FCS n Append the R to the raw message. The result J is the frame to be transmitted J=Q. xn-k+F n J should be exactly divisible by P Dividing Q. xn-k by P gives Q. xn-k/P=Q+R/P n Where R is the reminder n-k+R. This value of J should yield a zero n J=Q. x reminder for J/P Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 21

Common CRC Codes Code-Parity check bits Generator polynomial g(x) CRC-12 CRC-16 CRC-CCITT CRC-32 x 12 +x 11+x 3+x 2+x+1 x 16 +x 15+x 2+1 x 16 +x 12+x 5+1 x 32 +x 26+x 23+x 22+x 16 +x 12+x 11+x 10+x 8+x 7+x 5+x 4+x 2+x+1 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 22

Common CRC Codes Code Generator polynomial g(x) Parity check bits CRC-12 1+x+x 2+x 3+x 11+x 12 12 CRC-16 1+x 2+x 15+x 16 16 CRC-CCITT 1+x 5+x 16 16 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 23

Convolutional Codes n n n Most widely used channel code Encoding of information stream rather than information blocks Decoding is mostly performed by the Viterbi Algorithm (not covered here) The constraint length K for a convolution code is defined as K=M+1 where M is the maximum number of stages in any shift register The code rate r is defined as r = k/n where k is the number of parallel information bits and n is the number of parallel output encoded bits at one time interval A convolution code encoder with n=2 and k=1 or code rate r=1/2 is shown next Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 24

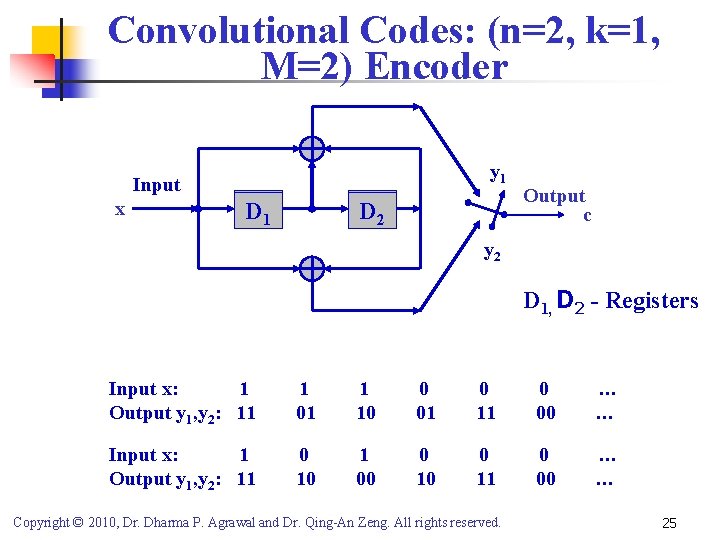
Convolutional Codes: (n=2, k=1, M=2) Encoder 1 1 yy 11 1 0 Input x 0 D 1 01 D 2 D 02 1 Output c y 1 y 22 0 D 1, D 2 - Registers Input x: 1 Output y 1, y 2: 11 1 01 1 10 0 01 0 11 0 00 … … Input x: 1 Output y 1, y 2: 11 0 10 1 00 0 11 0 00 … … Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 25

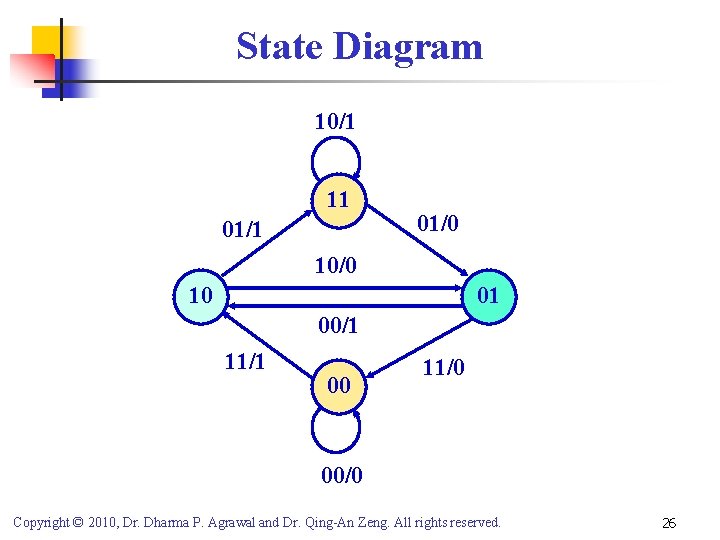
State Diagram 10/1 11 01/0 10/0 10 01 00/1 11/1 00 11/0 00/0 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 26

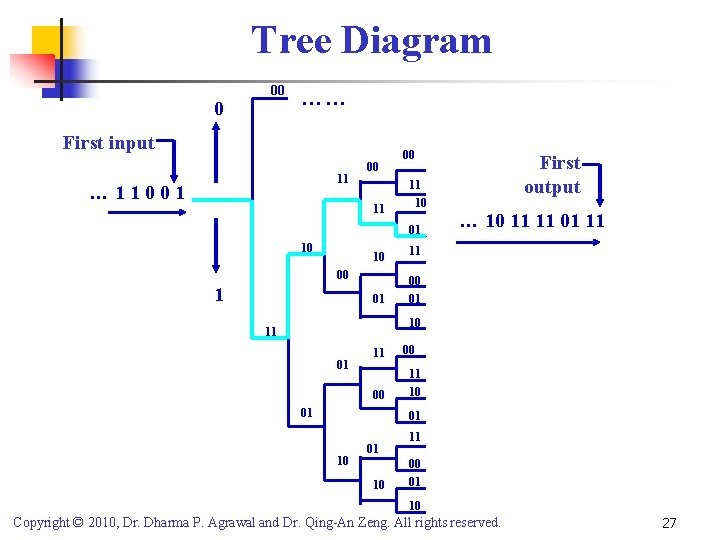
Tree Diagram 0 00 …… First input 11 … 11001 00 11 10 01 10 10 11 01 00 1 First output … 10 11 11 01 11 10 11 01 11 00 01 00 11 10 01 10 11 00 01 10 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 27

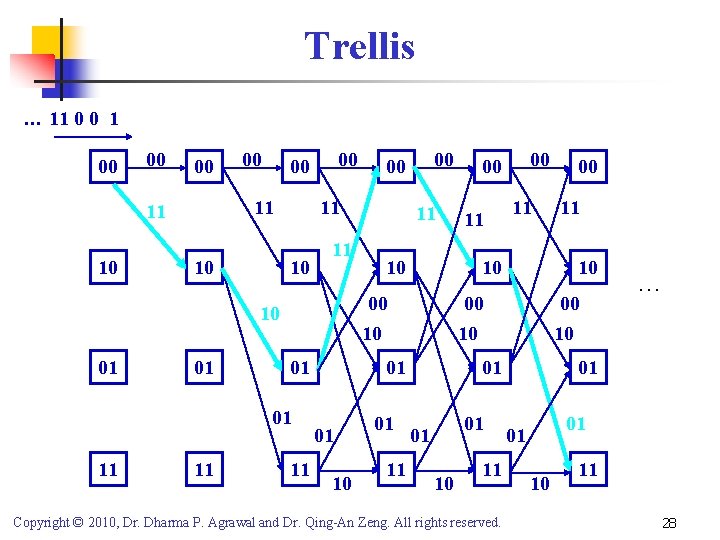
Trellis … 11 0 0 1 00 00 00 11 11 10 00 10 11 01 01 01 11 10 01 11 11 11 01 10 11 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 11 00 10 01 01 00 00 10 10 01 00 00 … 01 01 01 10 11 28

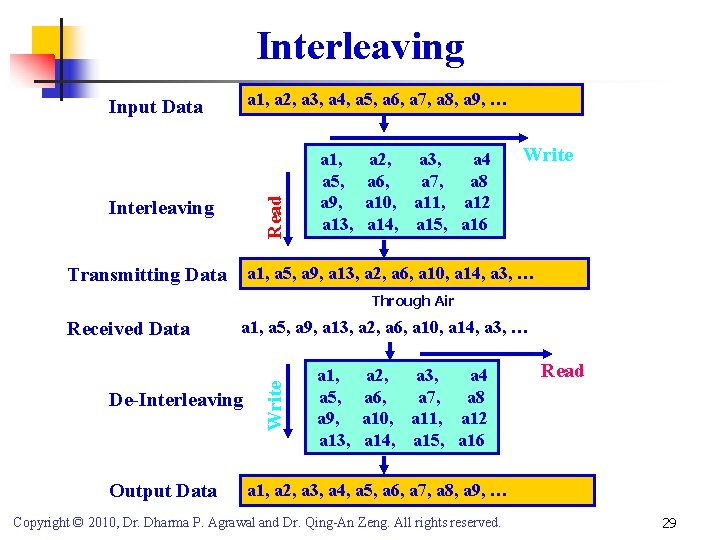
Interleaving a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8, a 9, … Read Input Data Interleaving a 1, a 5, a 9, a 13, a 2, a 3, a 4 a 6, a 7, a 8 a 10, a 11, a 12 a 14, a 15, a 16 Write a 1, a 5, a 9, a 13, a 2, a 6, a 10, a 14, a 3, … Transmitting Data Through Air a 1, a 5, a 9, a 13, a 2, a 6, a 10, a 14, a 3, … De-Interleaving Output Data Write Received Data a 1, a 5, a 9, a 13, a 2, a 3, a 4 a 6, a 7, a 8 a 10, a 11, a 12 a 14, a 15, a 16 Read a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8, a 9, … Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 29

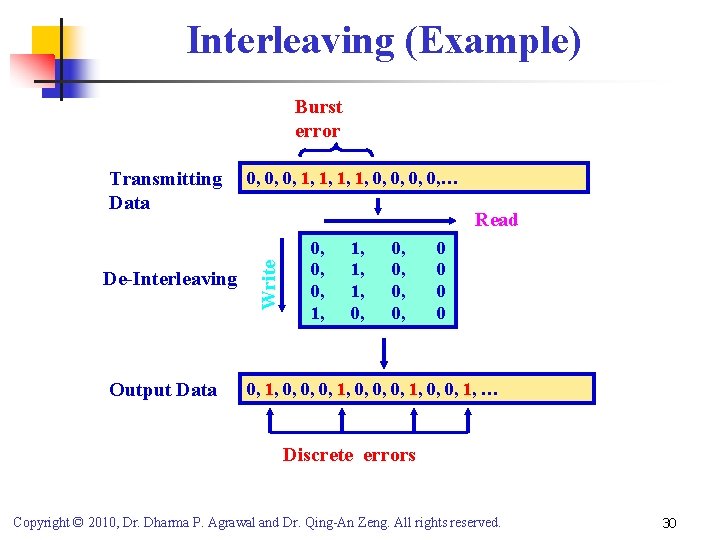
Interleaving (Example) Burst error De-Interleaving Output Data 0, 0, 0, 1, 1, 0, 0, … Read Write Transmitting Data 0, 0, 0, 1, 1, 1, 0, 0, 0 0 0, 1, 0, 0, 1, … Discrete errors Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 30

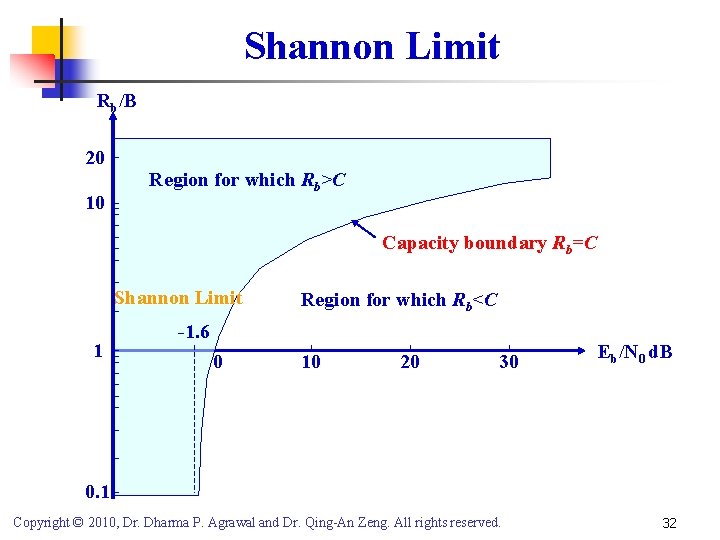
Information Capacity Theorem (Shannon Limit) n The information capacity (or channel capacity) C of a continuous channel with bandwidth B Hertz can be perturbed by additive Gaussian white noise of power spectral density N 0/2, provided bandwidth B satisfies where P is the average transmitted power P = Eb. Rb (for an ideal system, Rb = C) Eb is the transmitted energy per bit Rb is transmission rate Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 31

Shannon Limit Rb/B 20 10 Region for which Rb>C Capacity boundary Rb=C Shannon Limit 1 Region for which Rb<C -1. 6 0 10 20 30 Eb/N 0 d. B 0. 1 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 32

Turbo Codes n n A brief historic of turbo codes: The turbo code concept was first introduced by C. Berrou in 1993. Today, Turbo Codes are considered as the most efficient coding schemes for FEC Scheme with known components (simple convolutional or block codes, interleaver, soft-decision decoder, etc. ) Performance close to the Shannon Limit (Eb/N 0 = -1. 6 db if Rb 0) at modest complexity! Turbo codes have been proposed for low-power applications such as deep-space and satellite communications, as well as for interference limited applications such as third generation cellular, personal communication services, ad hoc and sensor networks Copyright © 2011, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 33

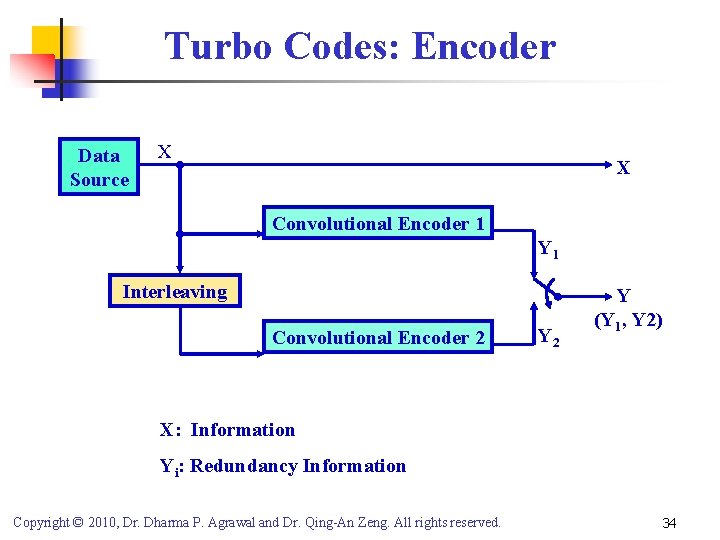
Turbo Codes: Encoder Data Source X X Convolutional Encoder 1 Y 1 Interleaving Convolutional Encoder 2 Y (Y 1, Y 2) X: Information Yi: Redundancy Information Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 34

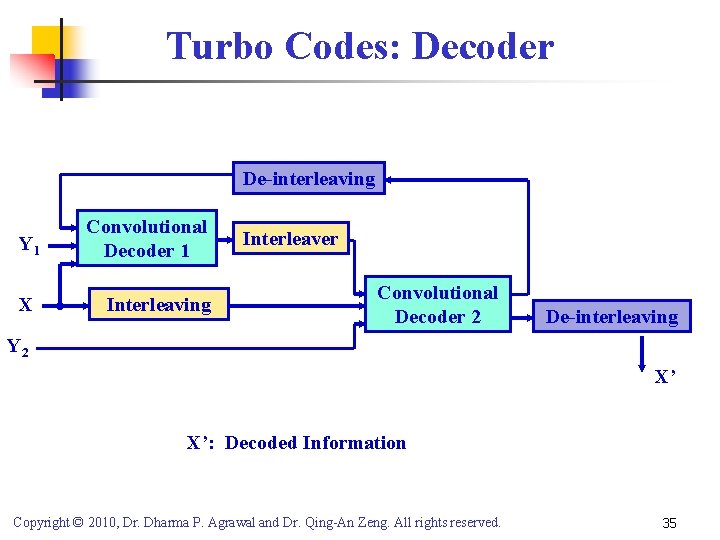
Turbo Codes: Decoder De-interleaving Y 1 X Convolutional Decoder 1 Interleaving Interleaver Convolutional Decoder 2 De-interleaving Y 2 X’ X’: Decoded Information Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 35

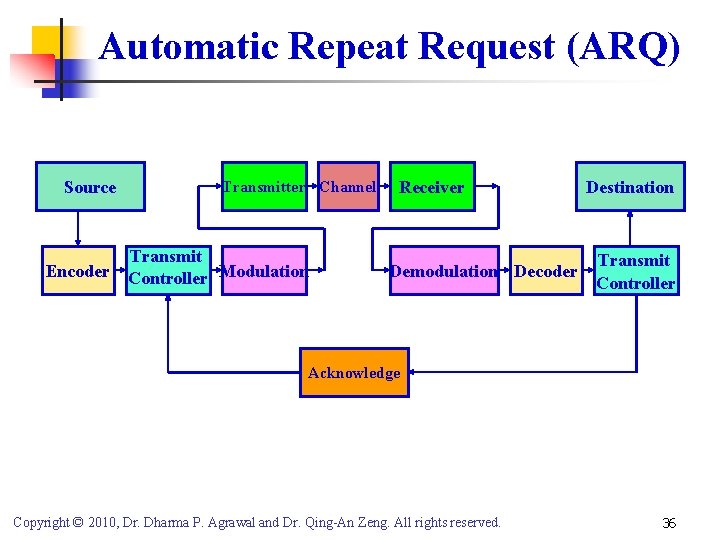
Automatic Repeat Request (ARQ) Source Transmitter Channel Transmit Encoder Controller Modulation Receiver Demodulation Decoder Destination Transmit Controller Acknowledge Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 36

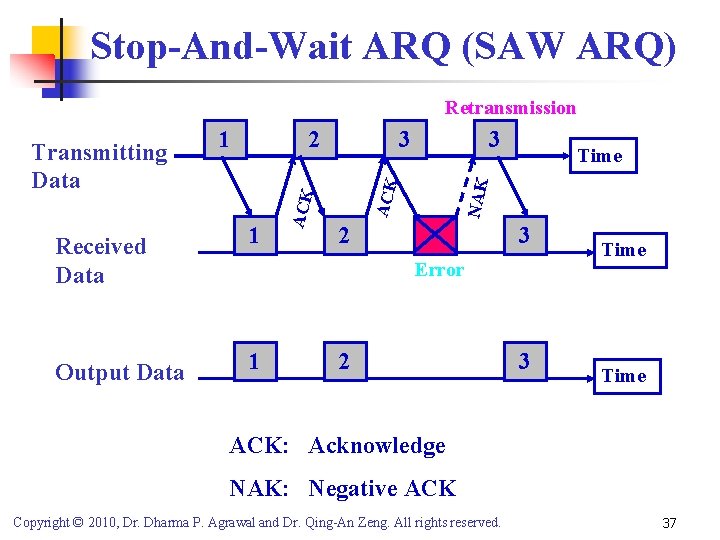
Stop-And-Wait ARQ (SAW ARQ) Retransmission Received Data 1 Output Data 1 3 3 Time NAK 2 ACK 1 ACK Transmitting Data 2 3 Error 2 3 Time ACK: Acknowledge NAK: Negative ACK Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 37

Stop-And-Wait ARQ (SAW ARQ) Throughput: SSAW = (1/TSAW). (k/n) = [(1 - Pb)n / (1 + D * Rb/ n) ] * (k/n) where TSAW is the average transmission time in terms of a block duration TSAW = (1 + D. Rb/ n). PACK + 2 (1 + D Rb/ n) PACK (1 - PACK) + 3 (1 + D Rb/ n) PACK (1 - PACK)2 + …. . = (1+ D Rb/n) PACK i (1 -PACK)i-1 = (1+ D Rb/n) PACK/[1 -(1 -PACK)]2 = (1 + D Rb/ n) / PACK where n = number of bits in a block, k = number of information bits in a block, D = round trip delay, Rb= bit rate, Pb = BER of the channel, and PACK (1 - Pb)n Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 38

Stop-And-Wait ARQ (SAW ARQ) Throughput: SSAW = (1/TSAW). (k/n) = [(1 - Pb)n / (1 + D * Rb/ n) ] * (k/n) where TSAW is the average transmission time in terms of a block duration TSAW = (1 + D. Rb/ n). PACK + 2 (1 + D Rb/ n) PACK (1 - PACK) + 3 (1 + D Rb/ n) PACK (1 - PACK)2 + …. . = (1+ D Rb/n) PACK i (1 -PACK)i-1 = (1+ D Rb/n) PACK/[1 -(1 -PACK)]2 = (1 + D Rb/ n) / PACK where n = number of bits in a block, k = number of information bits in a block, D = round trip delay, Rb= bit rate, Pb = BER of the channel, and PACK (1 - Pb)n Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 39

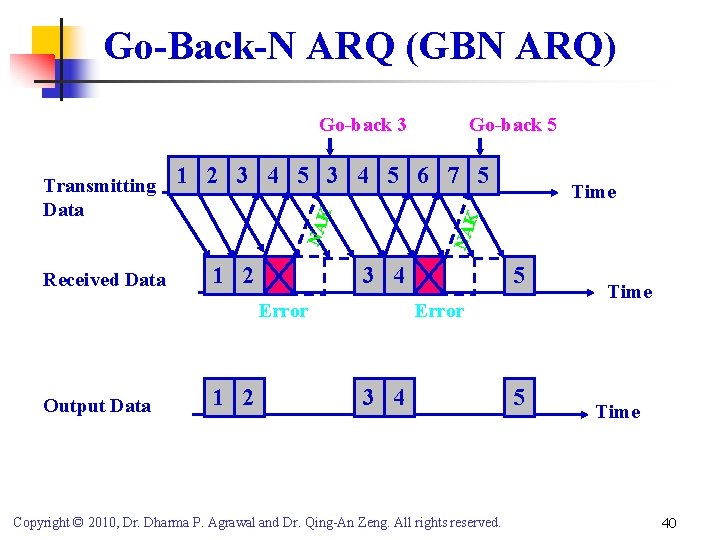
Go-Back-N ARQ (GBN ARQ) Go-back 3 Received Data 1 2 NA 3 4 Error Output Data 1 2 Time K K 1 2 3 4 5 6 7 5 NA Transmitting Data Go-back 5 5 Error 3 4 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 5 Time 40

Go-Back-N ARQ (GBN ARQ) Throughput SGBN = (1/TGBN) (k/n) = [(1 - Pb)n / ((1 - Pb)n + N (1 -(1 - Pb)n ) )] (k/n) where TGBN = 1. PACK + (N+1). PACK. (1 - PACK) +2. (N+1). PACK. (1 - PACK)2 + …. = PACK+PACK [(1 -PACK)+(1 -PACK )2 +(1 -PACK)3+…]+ PACK[N (1 -PACK)+2 N (1 -PACK )2 +3 N (1 -PACK)3+…] = PACK+PACK [(1 -PACK)/{1 -(1 -PACK )}+ N (1 -PACK)/{1 -(1 -PACK)}2] = 1+ N(1 -PACK)/PACK 1 + (N [1 - (1 - Pb)n ])/ (1 - Pb)n Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 41

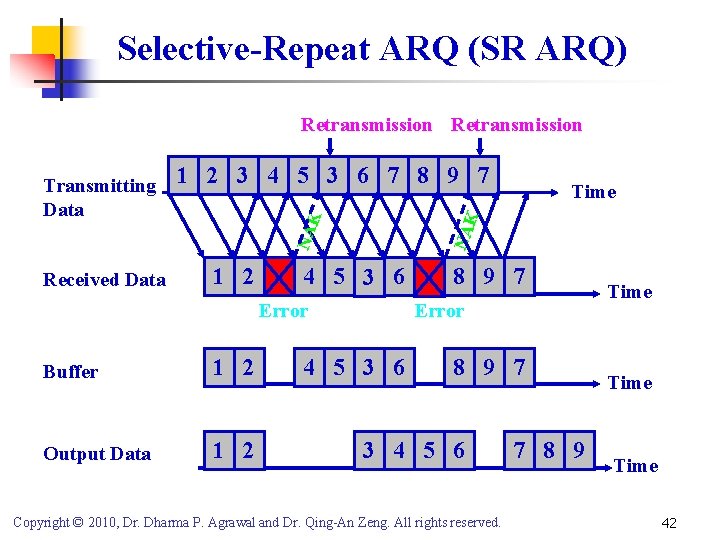
Selective-Repeat ARQ (SR ARQ) Retransmission 1 2 3 4 5 3 6 7 8 9 7 Received Data 1 2 K 4 5 3 6 Error Buffer 1 2 Output Data 1 2 Time NA K NA Transmitting Data 8 9 7 Error 4 5 3 6 8 9 7 3 4 5 6 Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 7 8 9 Time 42

Selective-Repeat ARQ (SR ARQ) Throughput SSR = (1/TSR) * (k/n) = (1 - Pb)n * (k/n) where TSR = 1. PACK + 2 PACK (1 - PACK) + 3 PACK (1 - PACK)2 + …. = PACK i (1 -PACK)i-1 = PACK/[1 -(1 -PACK)]2 = 1/(1 - Pb)n where PACK (1 -Pb)n Copyright © 2010, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 43