Chapter 4 Basic Nodal and Mesh Analysis Fig

Chapter 4 Basic Nodal and Mesh Analysis Fig. 4. 1 “Obtain values for the unknown voltages …” Fig. 4. 5 (a) The circuit of Example 4. 2 with a 22 -V source. . . User Note: Fig. 4. 7 “Determine the node-to-reference voltages …” Run View Show under the Slide Show menu to enable slide selection. Fig. 4. 9 Examples of planar and nonplanar networks. . . Fig. 4. 10 (a) The set of branches identified by the heavy lines… Fig. 4. 12 “Determine the two mesh currents, i 1 and i 2, in …” Fig. 4. 16 “Find the three mesh currents in the circuit below. ” Fig. 4. 19 Circuit from Practice Problem 4. 8. Engineering Circuit Analysis Sixth Edition W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin Copyright © 2002 Mc. Graw-Hill, Inc. All Rights Reserved.

Nodal Analysis
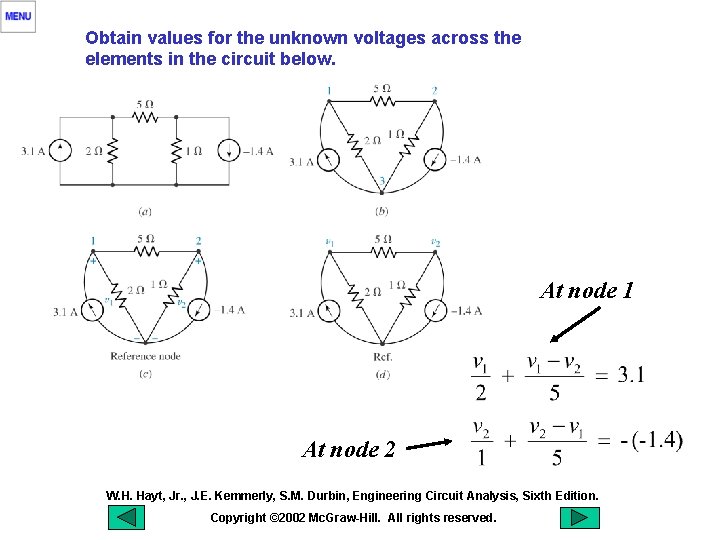
Obtain values for the unknown voltages across the elements in the circuit below. At node 1 At node 2 W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.
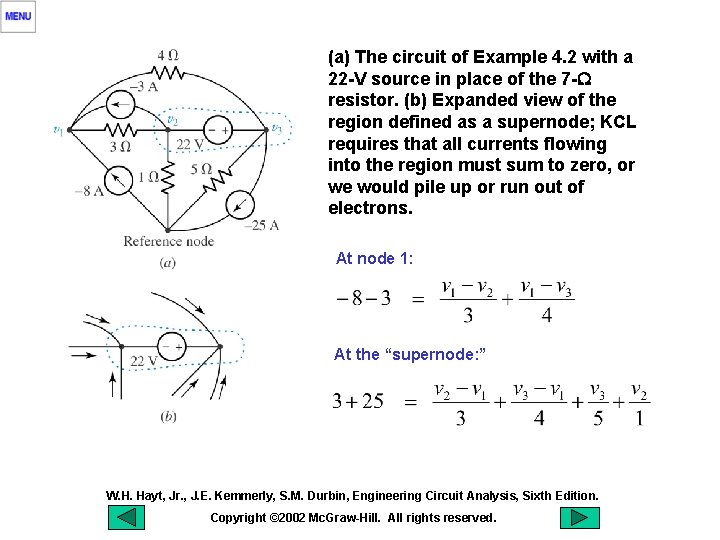
(a) The circuit of Example 4. 2 with a 22 -V source in place of the 7 -W resistor. (b) Expanded view of the region defined as a supernode; KCL requires that all currents flowing into the region must sum to zero, or we would pile up or run out of electrons. At node 1: At the “supernode: ” W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.

Determine the node-to-reference voltages in the circuit below. W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.
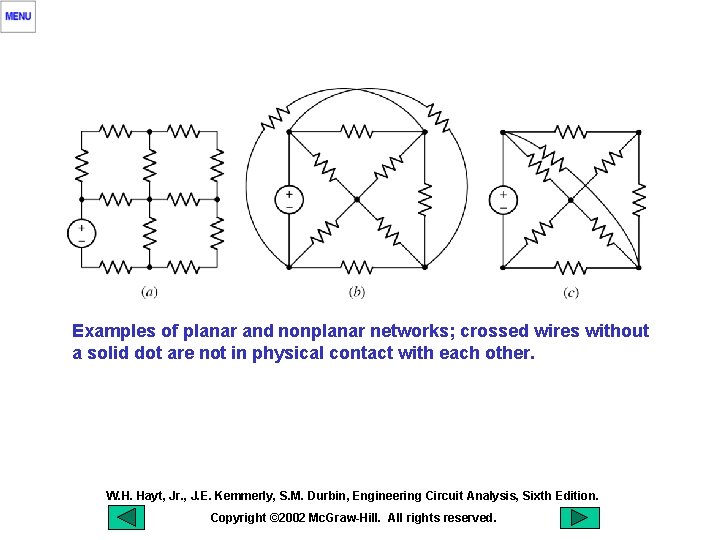
Examples of planar and nonplanar networks; crossed wires without a solid dot are not in physical contact with each other. W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.

(a) The set of branches identified by the heavy lines is neither a path nor a loop. (b) The set of branches here is not a path, since it can be traversed only by passing through the central node twice. (c) This path is a loop but not a mesh, since it encloses other loops. (d) This path is also a loop but not a mesh. (e, f) Each of these paths is both a loop and a mesh. W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.
Mesh Current Analysis
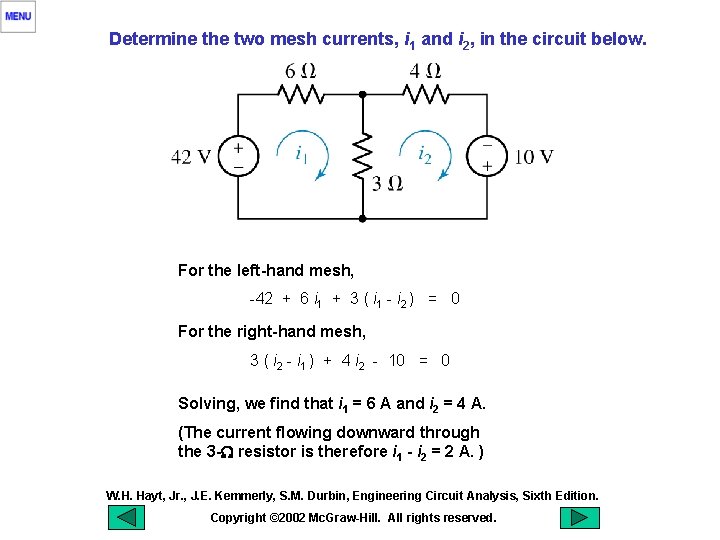
Determine the two mesh currents, i 1 and i 2, in the circuit below. For the left-hand mesh, -42 + 6 i 1 + 3 ( i 1 - i 2 ) = 0 For the right-hand mesh, 3 ( i 2 - i 1 ) + 4 i 2 - 10 = 0 Solving, we find that i 1 = 6 A and i 2 = 4 A. (The current flowing downward through the 3 -W resistor is therefore i 1 - i 2 = 2 A. ) W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.
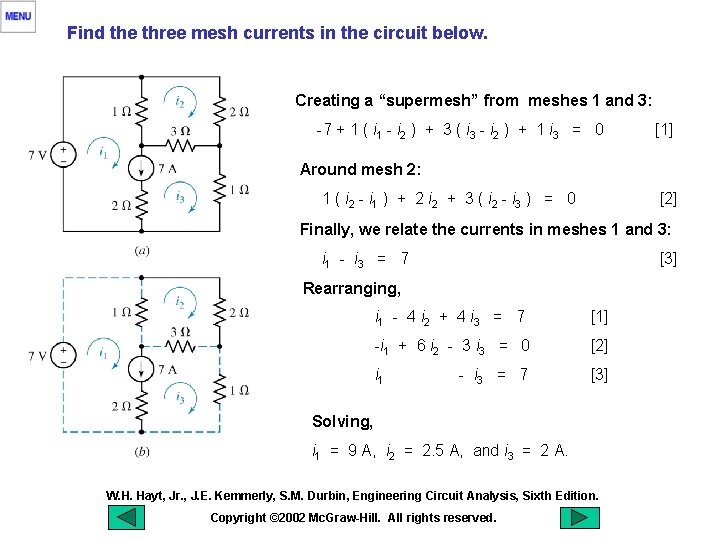
Find the three mesh currents in the circuit below. Creating a “supermesh” from meshes 1 and 3: -7 + 1 ( i 1 - i 2 ) + 3 ( i 3 - i 2 ) + 1 i 3 = 0 [1] Around mesh 2: 1 ( i 2 - i 1 ) + 2 i 2 + 3 ( i 2 - i 3 ) = 0 [2] Finally, we relate the currents in meshes 1 and 3: i 1 - i 3 = 7 [3] Rearranging, i 1 - 4 i 2 + 4 i 3 = 7 [1] -i 1 + 6 i 2 - 3 i 3 = 0 [2] i 1 [3] - i 3 = 7 Solving, i 1 = 9 A, i 2 = 2. 5 A, and i 3 = 2 A. W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.
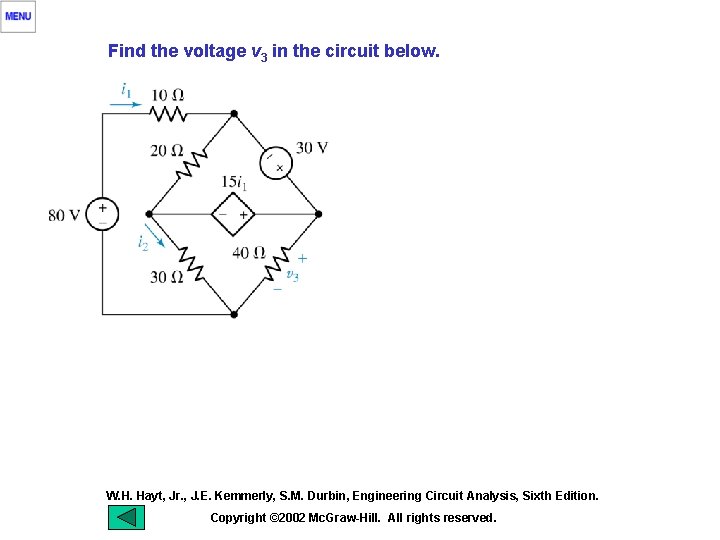
Find the voltage v 3 in the circuit below. W. H. Hayt, Jr. , J. E. Kemmerly, S. M. Durbin, Engineering Circuit Analysis, Sixth Edition. Copyright © 2002 Mc. Graw-Hill. All rights reserved.
- Slides: 11