Chapter 4 An introduction to molecular symmetry Dr

Chapter 4 An introduction to molecular symmetry Dr. Said M. El-Kurdi 1

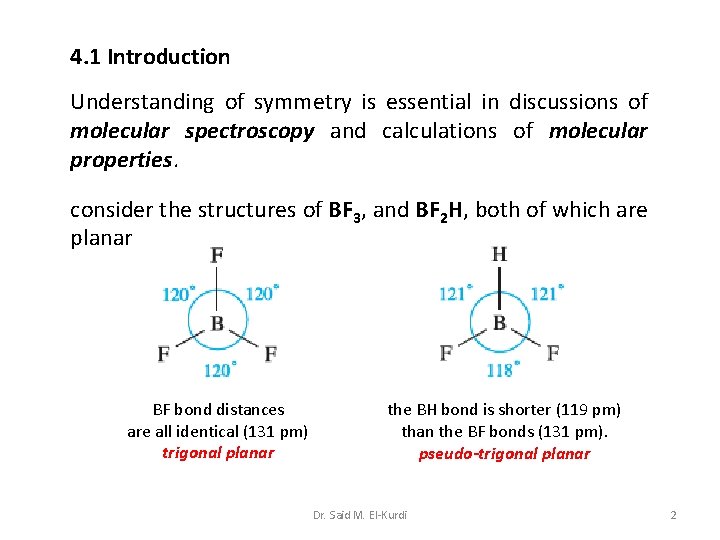
4. 1 Introduction Understanding of symmetry is essential in discussions of molecular spectroscopy and calculations of molecular properties. consider the structures of BF 3, and BF 2 H, both of which are planar BF bond distances are all identical (131 pm) trigonal planar the BH bond is shorter (119 pm) than the BF bonds (131 pm). pseudo-trigonal planar Dr. Said M. El-Kurdi 2

the molecular symmetry properties are not the same Group theory is the mathematical treatment of symmetry. In this chapter, we introduce the fundamental language of group theory (symmetry operator, symmetry element, point group and character table). Dr. Said M. El-Kurdi 3

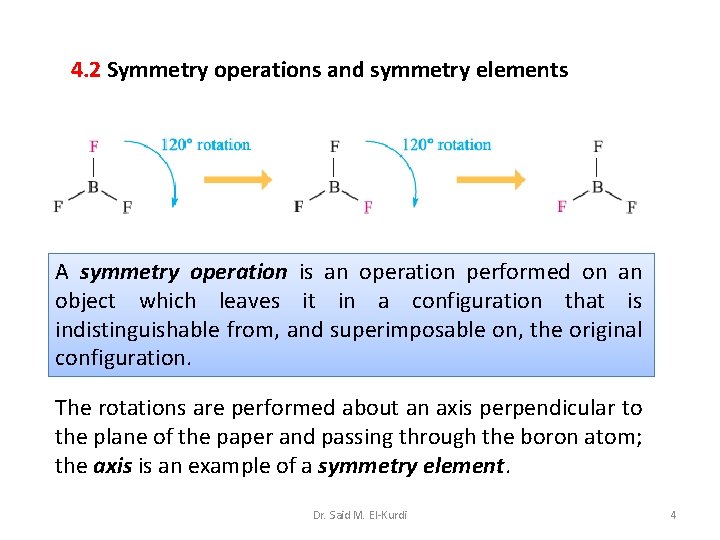
4. 2 Symmetry operations and symmetry elements A symmetry operation is an operation performed on an object which leaves it in a configuration that is indistinguishable from, and superimposable on, the original configuration. The rotations are performed about an axis perpendicular to the plane of the paper and passing through the boron atom; the axis is an example of a symmetry element. Dr. Said M. El-Kurdi 4

A symmetry operation is carried out with respect to points, lines or planes, the latter being the symmetry elements. Rotation about an n-fold axis of symmetry The symmetry operation of rotation about an n-fold axis (the symmetry element) is denoted by the symbol Cn, in which the angle of rotation is: n is an integer, e. g. 2, 3 or 4. Dr. Said M. El-Kurdi 5

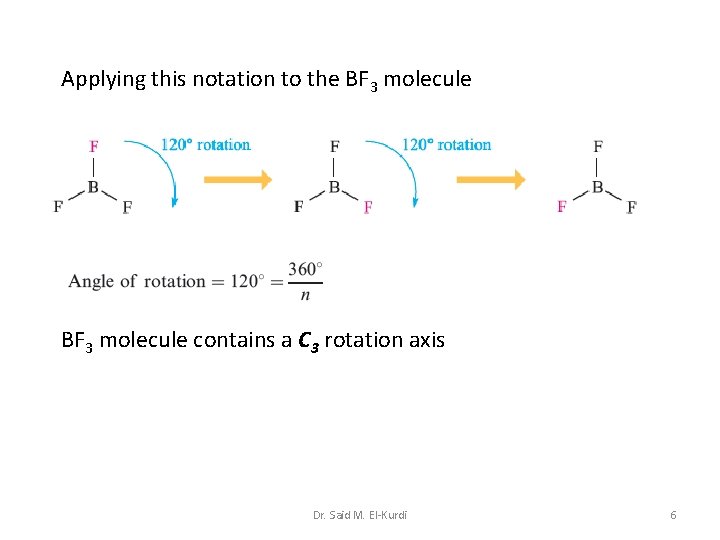
Applying this notation to the BF 3 molecule contains a C 3 rotation axis Dr. Said M. El-Kurdi 6

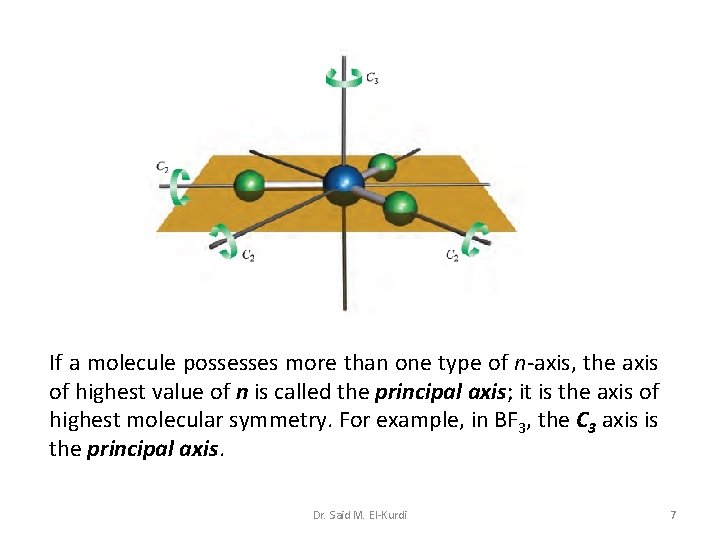
If a molecule possesses more than one type of n-axis, the axis of highest value of n is called the principal axis; it is the axis of highest molecular symmetry. For example, in BF 3, the C 3 axis is the principal axis. Dr. Said M. El-Kurdi 7

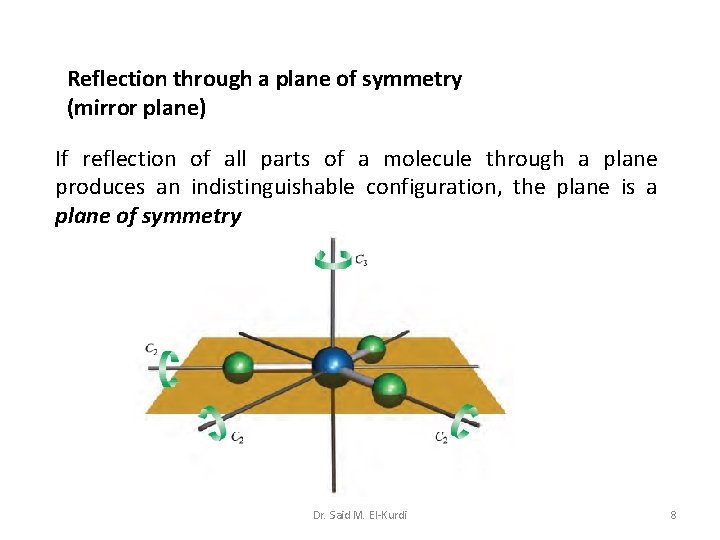
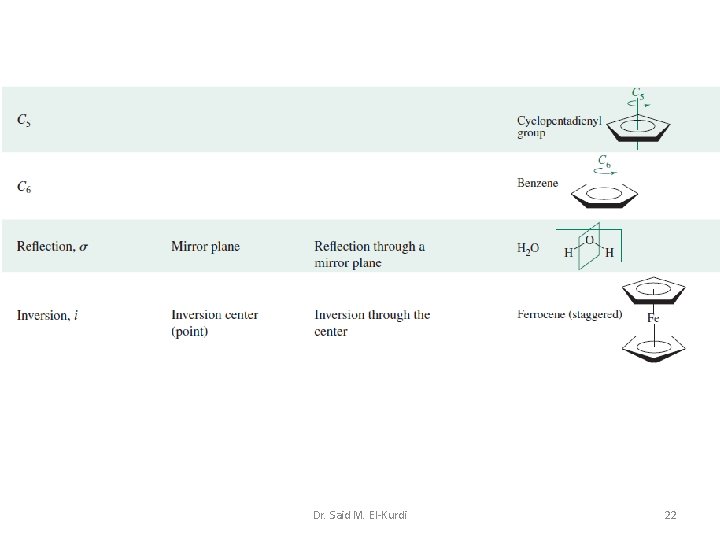
Reflection through a plane of symmetry (mirror plane) If reflection of all parts of a molecule through a plane produces an indistinguishable configuration, the plane is a plane of symmetry Dr. Said M. El-Kurdi 8

the symmetry operation is one of reflection and the symmetry element is the mirror plane (denoted by ) Ø If the plane lies perpendicular to the vertical principal axis, it is denoted by the symbol h. Ø If the plane contains the principal axis, it is labeled v. Dr. Said M. El-Kurdi 9

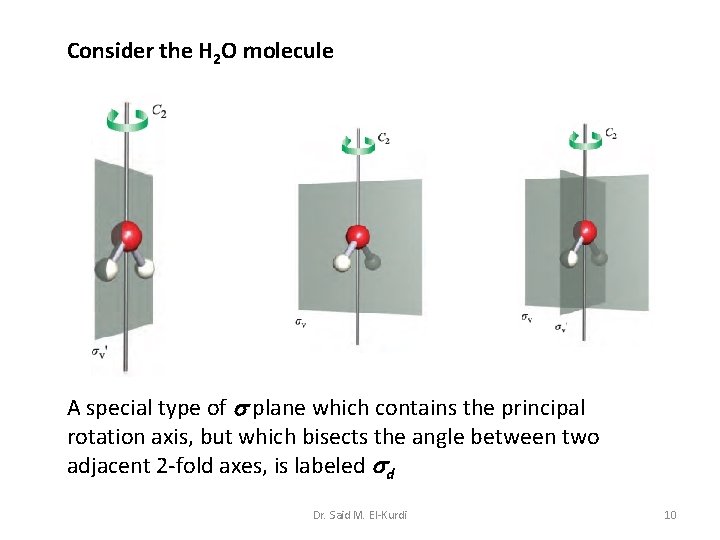
Consider the H 2 O molecule A special type of plane which contains the principal rotation axis, but which bisects the angle between two adjacent 2 -fold axes, is labeled d Dr. Said M. El-Kurdi 10

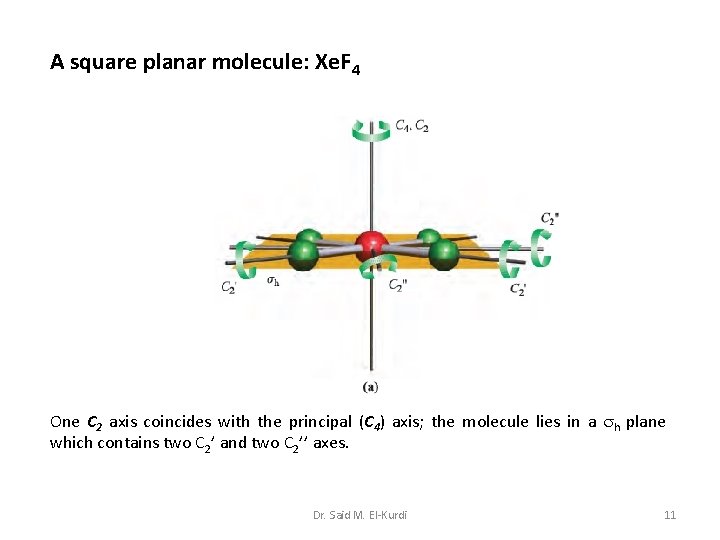
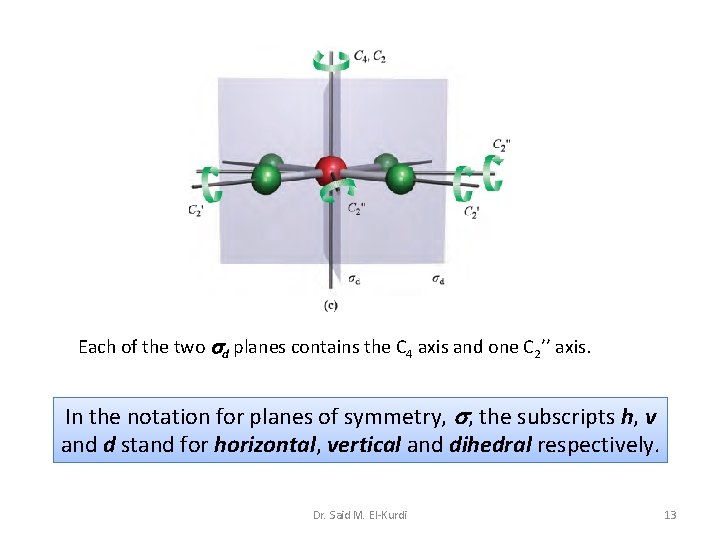
A square planar molecule: Xe. F 4 One C 2 axis coincides with the principal (C 4) axis; the molecule lies in a h plane which contains two C 2’ and two C 2’’ axes. Dr. Said M. El-Kurdi 11

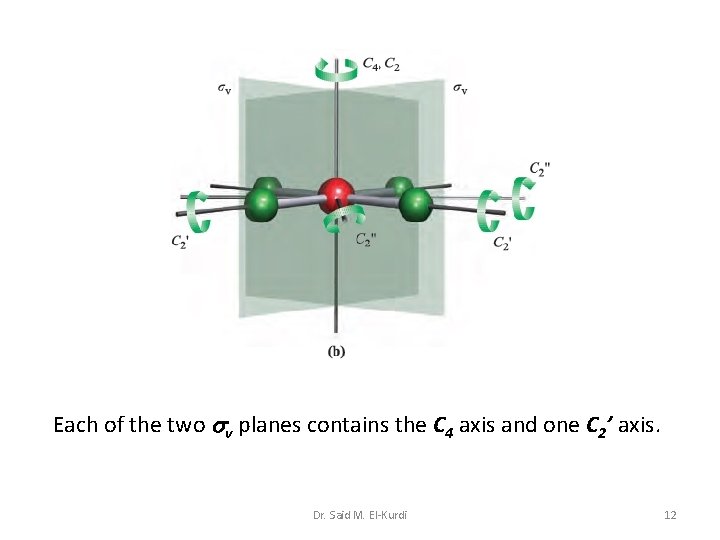
Each of the two v planes contains the C 4 axis and one C 2’ axis. Dr. Said M. El-Kurdi 12

Each of the two d planes contains the C 4 axis and one C 2’’ axis. In the notation for planes of symmetry, , the subscripts h, v and d stand for horizontal, vertical and dihedral respectively. Dr. Said M. El-Kurdi 13

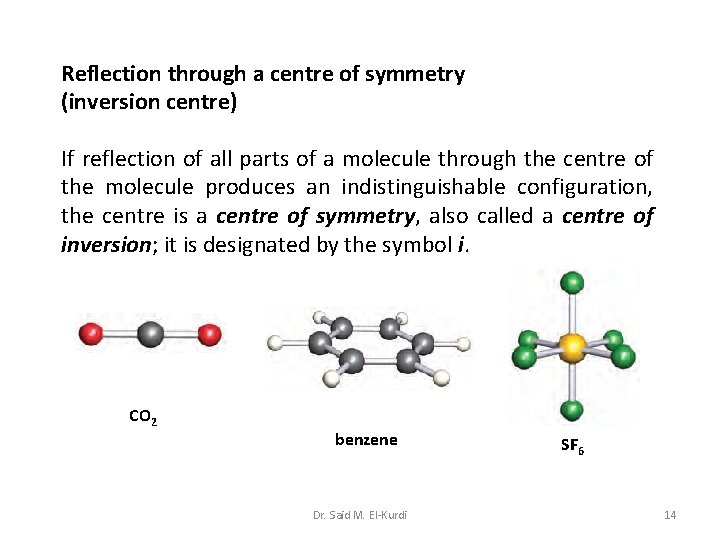
Reflection through a centre of symmetry (inversion centre) If reflection of all parts of a molecule through the centre of the molecule produces an indistinguishable configuration, the centre is a centre of symmetry, also called a centre of inversion; it is designated by the symbol i. CO 2 benzene Dr. Said M. El-Kurdi SF 6 14

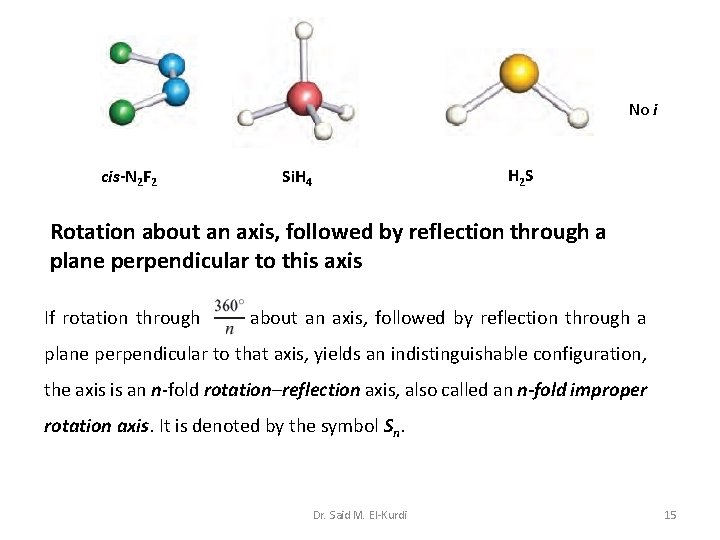
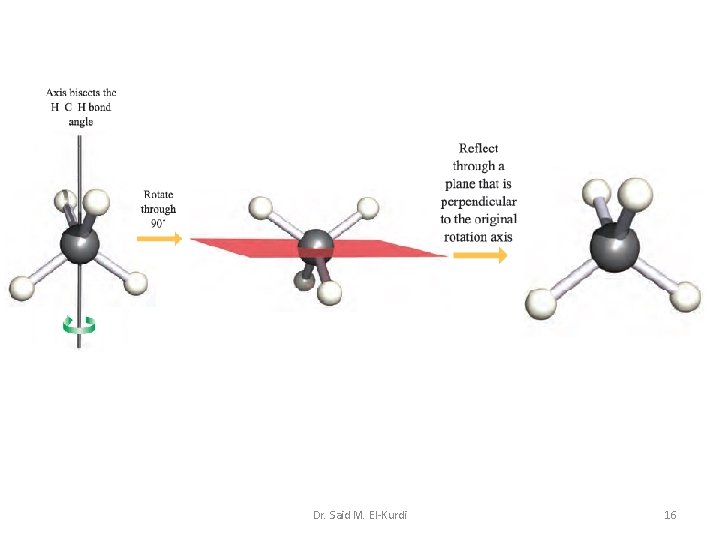
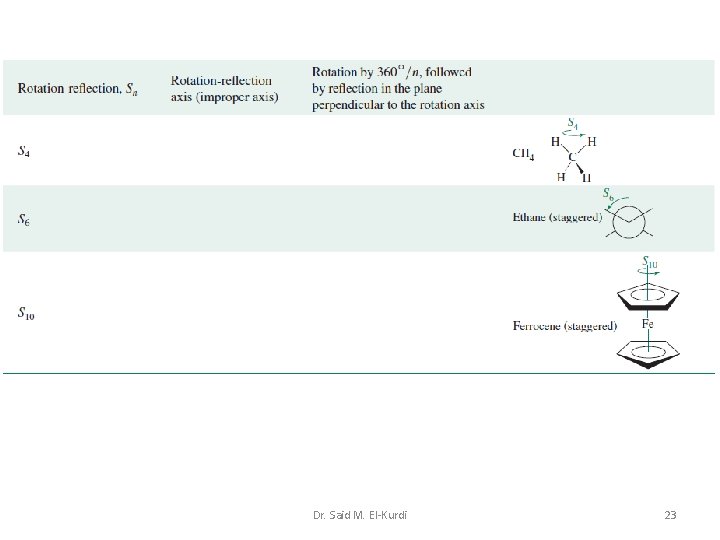
No i cis-N 2 F 2 H 2 S Si. H 4 Rotation about an axis, followed by reflection through a plane perpendicular to this axis If rotation through about an axis, followed by reflection through a plane perpendicular to that axis, yields an indistinguishable configuration, the axis is an n-fold rotation–reflection axis, also called an n-fold improper rotation axis. It is denoted by the symbol Sn. Dr. Said M. El-Kurdi 15

Dr. Said M. El-Kurdi 16

Identity operator All objects can be operated upon by the identity operator E. The operator E leaves the molecule unchanged. Dr. Said M. El-Kurdi 17

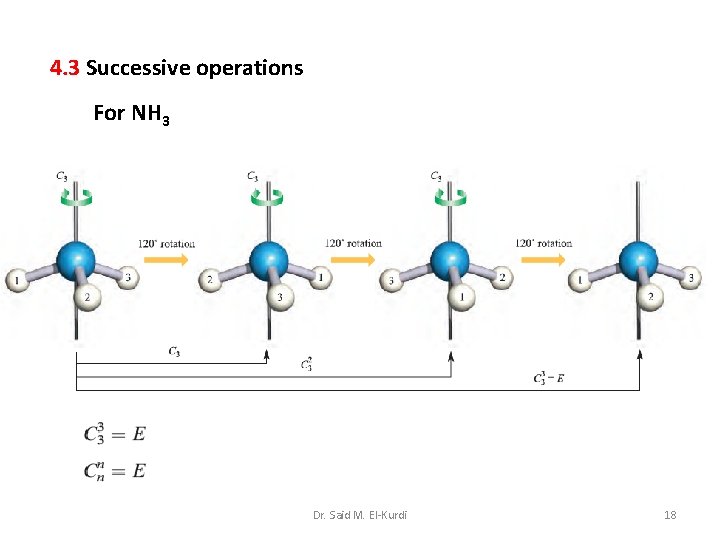
4. 3 Successive operations For NH 3 Dr. Said M. El-Kurdi 18

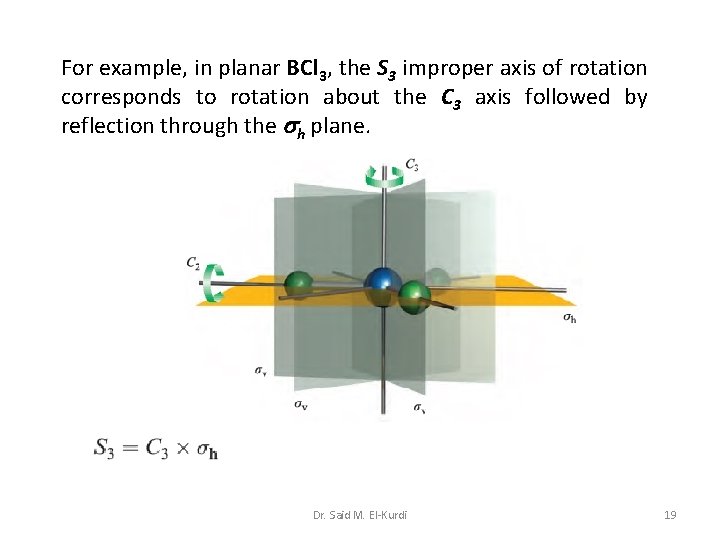
For example, in planar BCl 3, the S 3 improper axis of rotation corresponds to rotation about the C 3 axis followed by reflection through the h plane. Dr. Said M. El-Kurdi 19

Dr. Said M. El-Kurdi 20

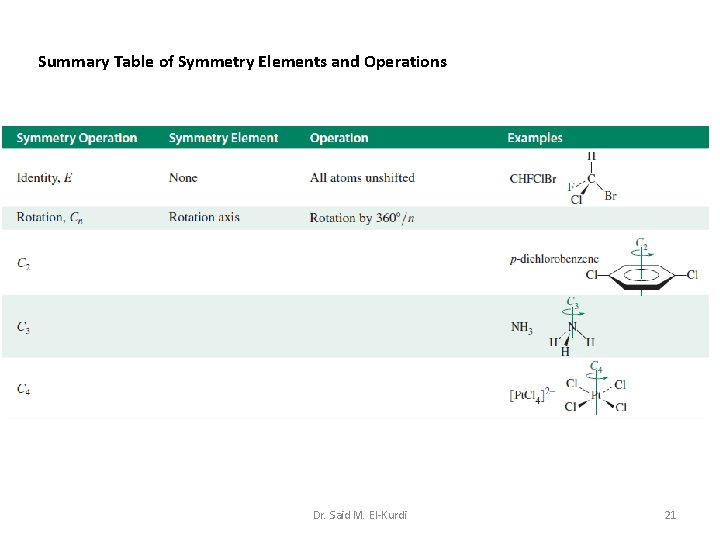
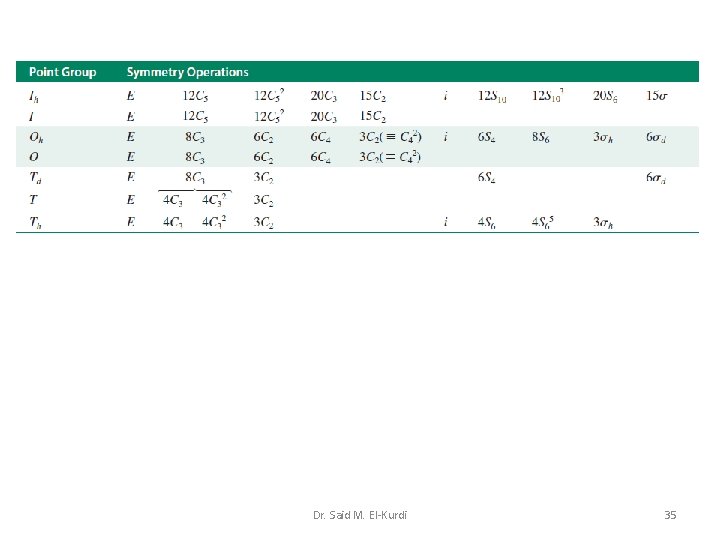
Summary Table of Symmetry Elements and Operations Dr. Said M. El-Kurdi 21

Dr. Said M. El-Kurdi 22

Dr. Said M. El-Kurdi 23

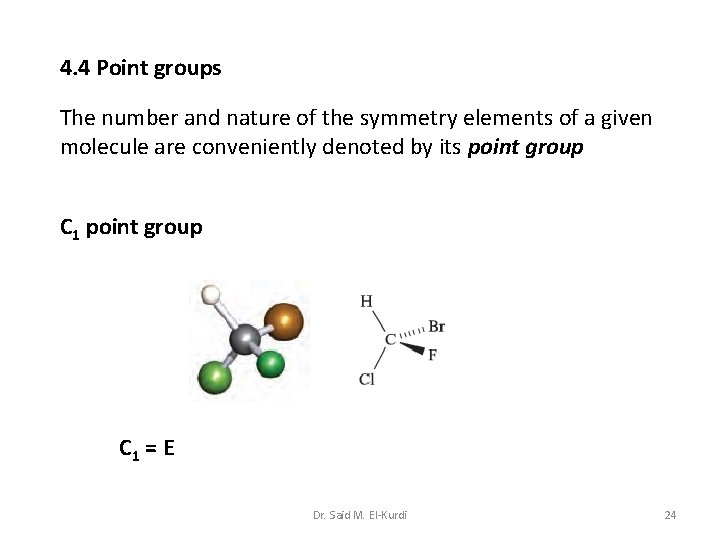
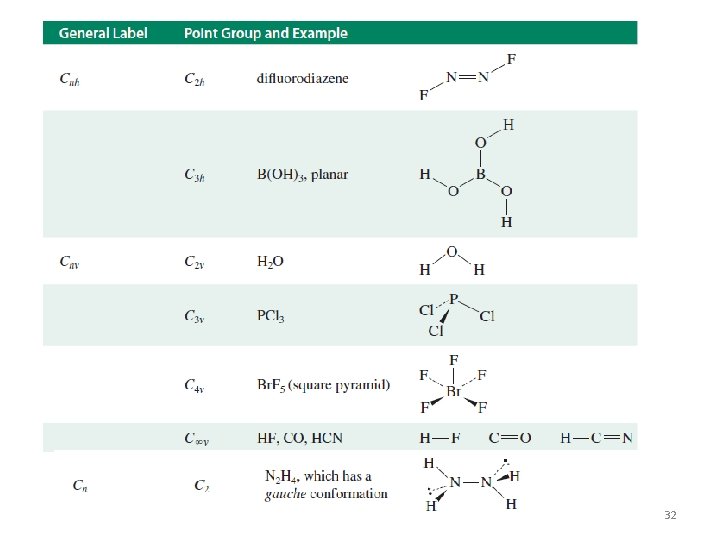
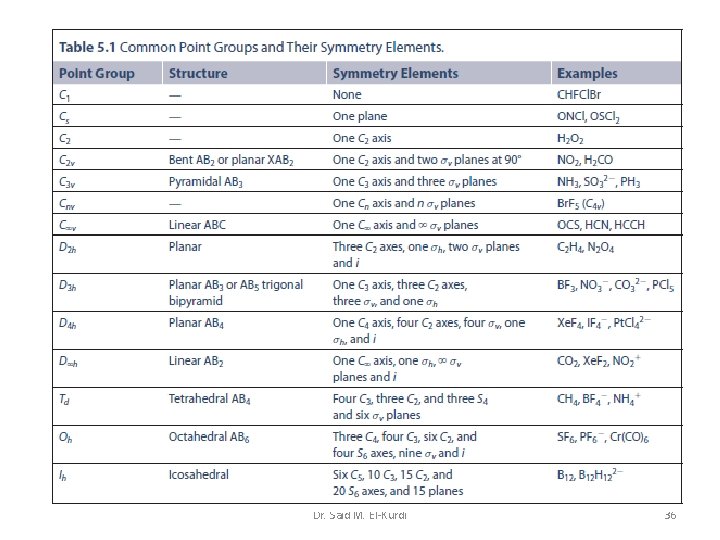
4. 4 Point groups The number and nature of the symmetry elements of a given molecule are conveniently denoted by its point group C 1 = E Dr. Said M. El-Kurdi 24

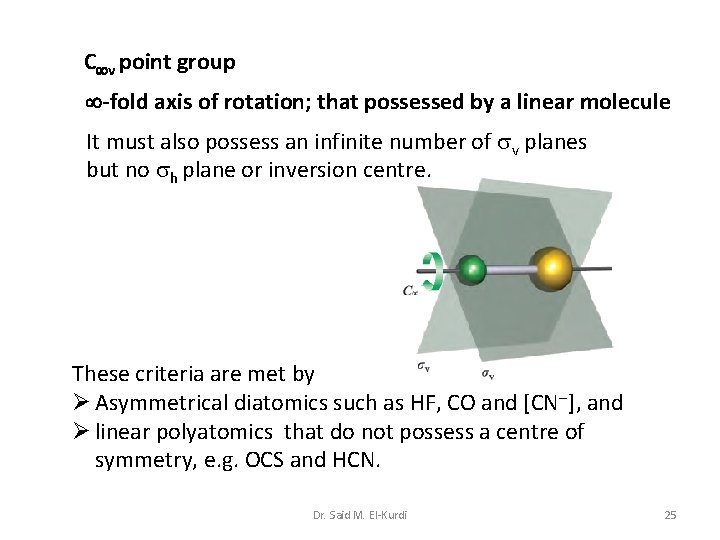
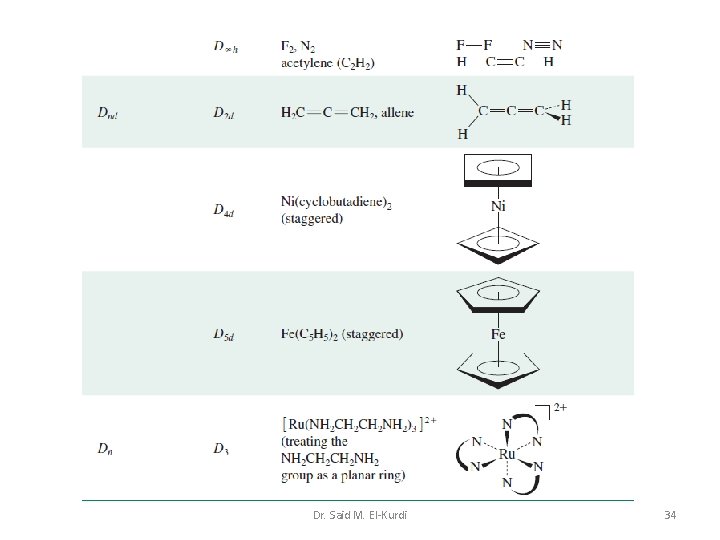
C v point group -fold axis of rotation; that possessed by a linear molecule It must also possess an infinite number of v planes but no h plane or inversion centre. These criteria are met by Ø Asymmetrical diatomics such as HF, CO and [CN ], and Ø linear polyatomics that do not possess a centre of symmetry, e. g. OCS and HCN. Dr. Said M. El-Kurdi 25

D h point group Ø Symmetrical diatomics (e. g. H 2, [O 2]2 ) and Ø linear polyatomics that contain a centre of symmetry (e. g. [N 3], CO 2, HCCH) possess a h plane in addition to a C axis and an infinite number of v planes Dr. Said M. El-Kurdi 26

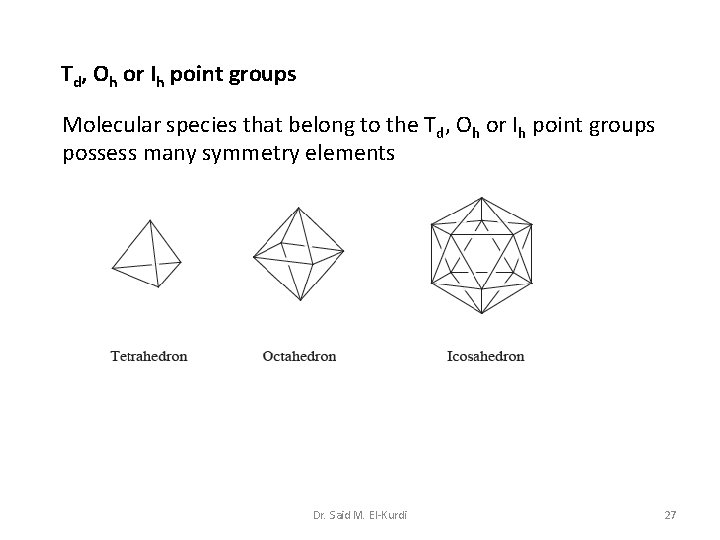
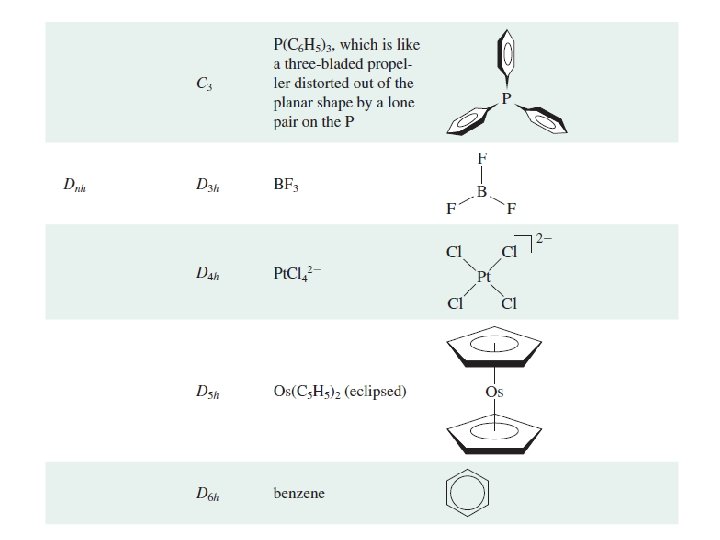
Td, Oh or Ih point groups Molecular species that belong to the Td, Oh or Ih point groups possess many symmetry elements Dr. Said M. El-Kurdi 27

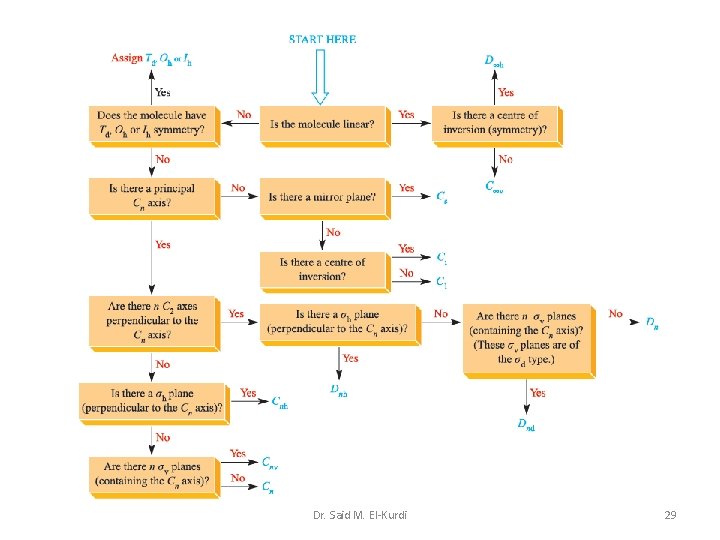
Determining the point group of a molecule or molecular ion Dr. Said M. El-Kurdi 28

Dr. Said M. El-Kurdi 29

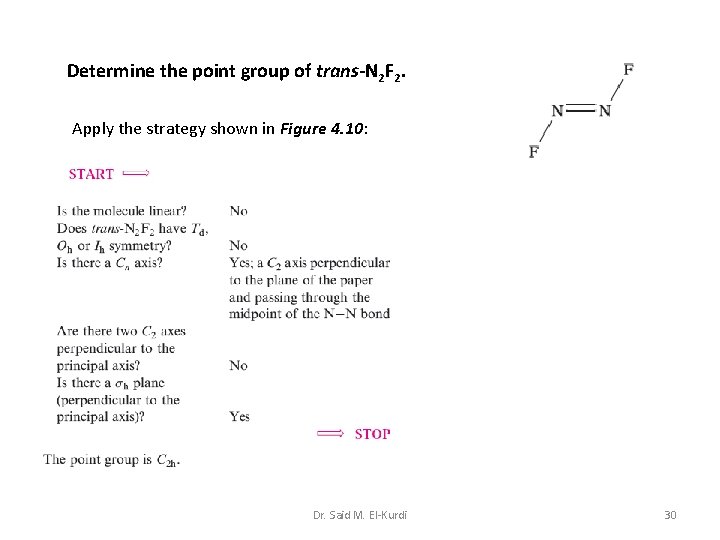
Determine the point group of trans-N 2 F 2. Apply the strategy shown in Figure 4. 10: Dr. Said M. El-Kurdi 30

Determine the point group of PF 5. Dr. Said M. El-Kurdi 31

Dr. Said M. El-Kurdi 32

Dr. Said M. El-Kurdi 33

Dr. Said M. El-Kurdi 34

Dr. Said M. El-Kurdi 35

Dr. Said M. El-Kurdi 36