Chapter 4 AC Machines Fundamental By Zetty Nurazlinda

Chapter 4 AC Machines Fundamental By Zetty Nurazlinda Zakaria

Review: Electromagnetism Magnetic field due to an electric current • Ø Ø When a conductor carries an electric current, a magnetic field is produced around that conductor. Determined by Thumb/Right Hand Rule. Flux, φ Current , I

�Magnetic field of a solenoid Ø If a coil is wound on a steel rod and connected to a supply, the steel becomes magnetized and behaves like a permanent magnet. Ø Grip Rule if solenoid is gripped with the right hand, with fingers pointing in the direction of current, then the thumb outdtretched parallel to the axis of the solenoid points in the direction of the magnetic field inside the solenoid. Solenoid with a steel core

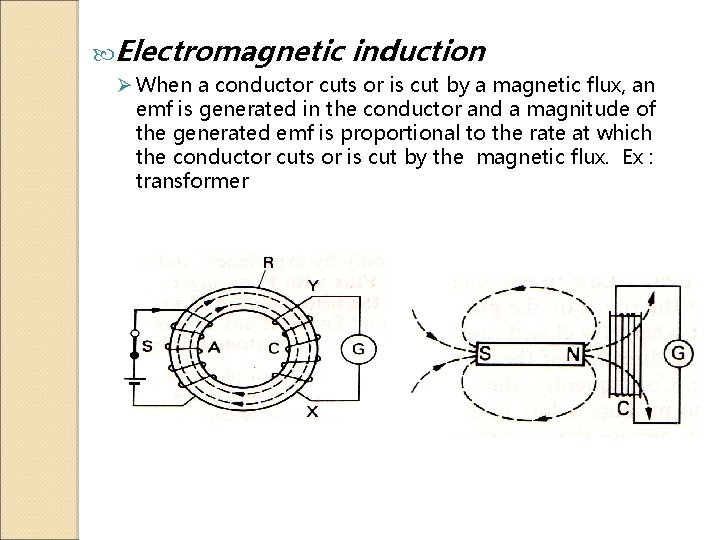
Electromagnetic induction Ø When a conductor cuts or is cut by a magnetic flux, an emf is generated in the conductor and a magnitude of the generated emf is proportional to the rate at which the conductor cuts or is cut by the magnetic flux. Ex : transformer

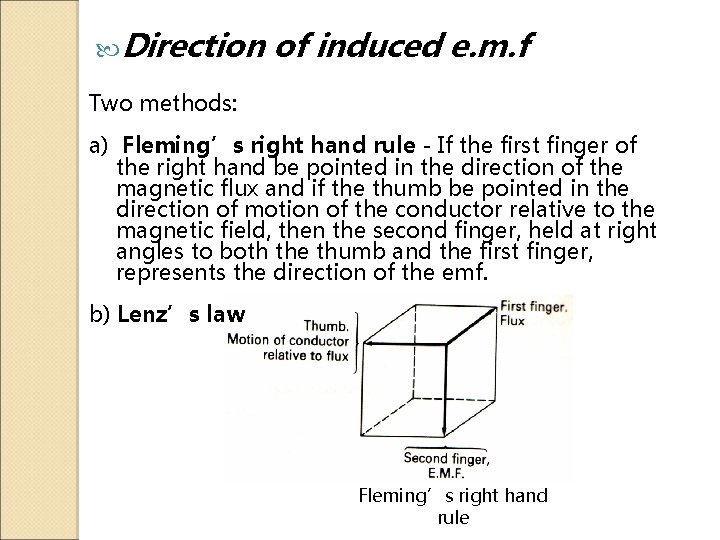
Direction of induced e. m. f Two methods: a) Fleming’s right hand rule - If the first finger of the right hand be pointed in the direction of the magnetic flux and if the thumb be pointed in the direction of motion of the conductor relative to the magnetic field, then the second finger, held at right angles to both the thumb and the first finger, represents the direction of the emf. b) Lenz’s law Fleming’s right hand rule

AC Machines Fundamental 4. 1 A SIMPLE LOOP IN A UNIFORM MAGNETIC A simple loop in a uniform magnetic field is the simplest possible machine that produces a sinusoidal ac voltage. This case is not representative of real ac machine, since the flux in real ac machines is not constant in either magnitude or direction. However, the factors that control the voltage and torque on the loop will be the same as the factors that control the voltage and torque in real ac machines. The rotating part of the machine called rotor, and the stationary part of the machine is called the stator.

4. 1. 1 THE VOLTAGE INDUCED IN A SIMPLE ROTATING LOOP (Generator principles) The voltage of each segment is: Where the velocity of the wire (v) is tangential to the path of rotation, while the magnetic field (B) points to the right. I = length of conductor in the magnetic field.

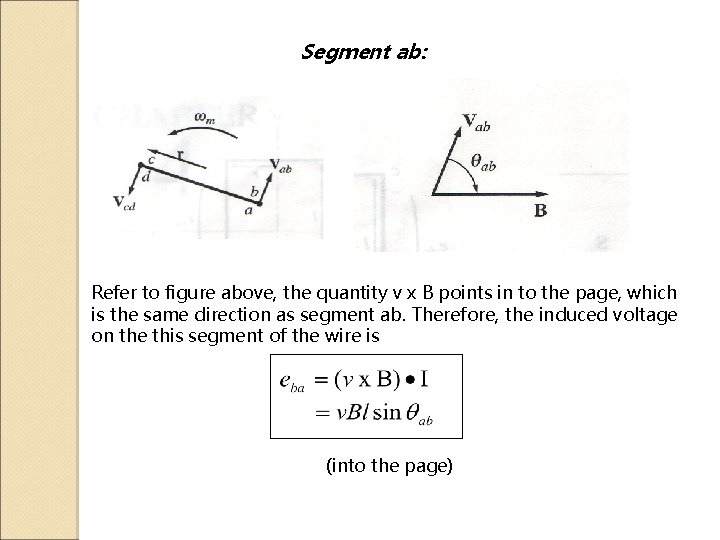
Segment ab: Refer to figure above, the quantity v x B points in to the page, which is the same direction as segment ab. Therefore, the induced voltage on the this segment of the wire is (into the page)

Segment bc: The quantity v x B points out of the page. Since the length l is in the plane of the page, v x B is perpendicular to I for both portions of the segment. Therefore the voltage in segment bc will be zero: , Segment cd: Refer to figure above; the quantity v x B points in to the page, which is the same direction as segment cd. Therefore, the induced voltage on the this segment of the wire is (out of the page)

Segment da: The quatity v x B points out of the page. Since the length l is in the plane of the page, v x B is perpendicular to I for both portions of the segemnt. Thefore the voltage in segment bc will be zero: So the total induced voltage on the loop, eind is the sum of the voltages on each of its sides:

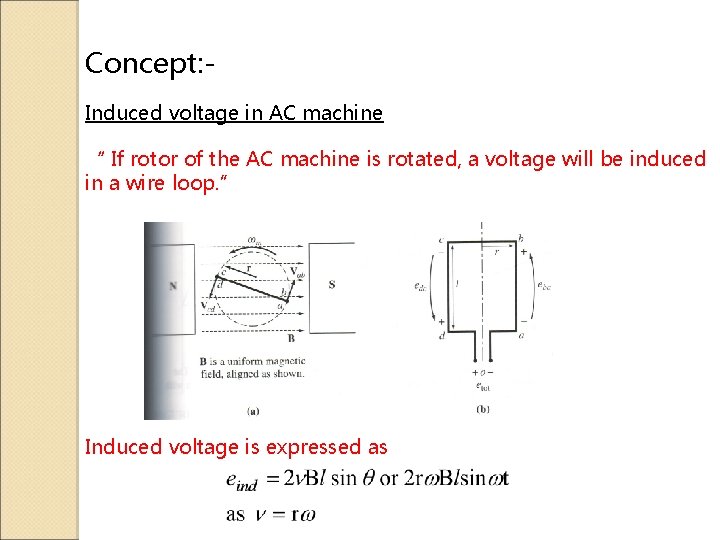
Concept: Induced voltage in AC machine “ If rotor of the AC machine is rotated, a voltage will be induced in a wire loop. ” Induced voltage is expressed as

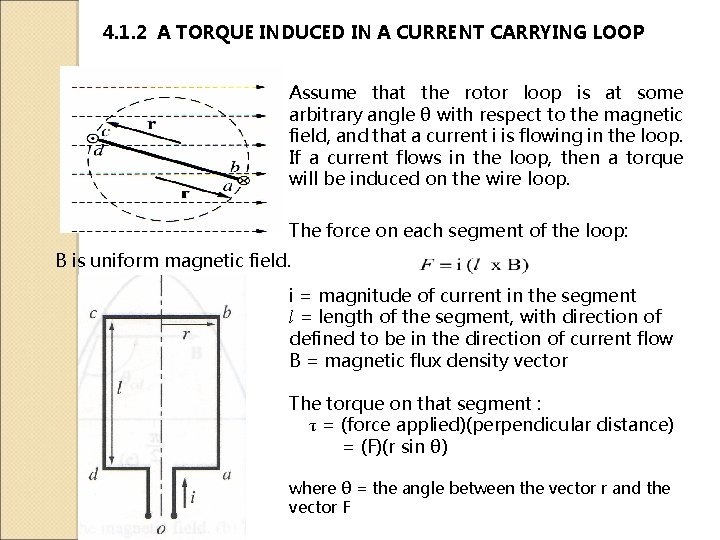
4. 1. 2 A TORQUE INDUCED IN A CURRENT CARRYING LOOP Assume that the rotor loop is at some arbitrary angle θ with respect to the magnetic field, and that a current i is flowing in the loop. If a current flows in the loop, then a torque will be induced on the wire loop. The force on each segment of the loop: B is uniform magnetic field. i = magnitude of current in the segment l = length of the segment, with direction of defined to be in the direction of current flow B = magnetic flux density vector The torque on that segment : τ = (force applied)(perpendicular distance) = (F)(r sin θ) where θ = the angle between the vector r and the vector F

Segment ab: The direction of the current is into the page, while the magnetic field B points to the right. The quantity I x B points down. The induced force on this segment of the wire: F = i (I x B) = i. IB (down) The resulting torque is

Segment bc: The direction of the current is in the plane the page, while the magnetic field B points to the right. The quantity I x B points into the page. The induced force on this segment of the wire: F = i (I x B) = i. IB (into the page) The resulting torque is 0, since vectors r and I are parallel (both point into the page), and the angle θbc is 0.

Segment cd: The direction of the current is out of the page, while the magnetic field B points to the right. The quantity I x B points up. The induced force on this segment of the wire: F = i (I x B) = i. IB (up) The resulting torque is

Segment da: The direction of the current is in the plane the page, while the magnetic field B points to the right. The quantity I x B points out of the page. The induced force on this segment of the wire: F = i (I x B) = i. IB (out of the page) The resulting torque is 0, since vectors r and I are parallel (both point out of the page), and the angle θda is 0.

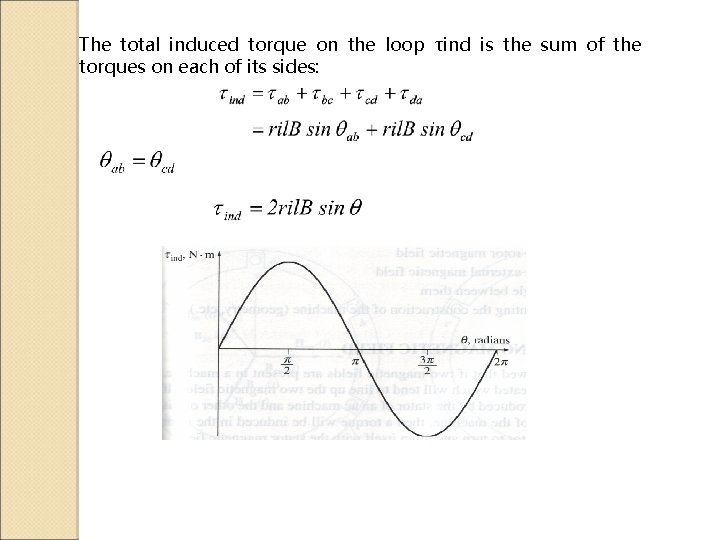
The total induced torque on the loop τind is the sum of the torques on each of its sides:

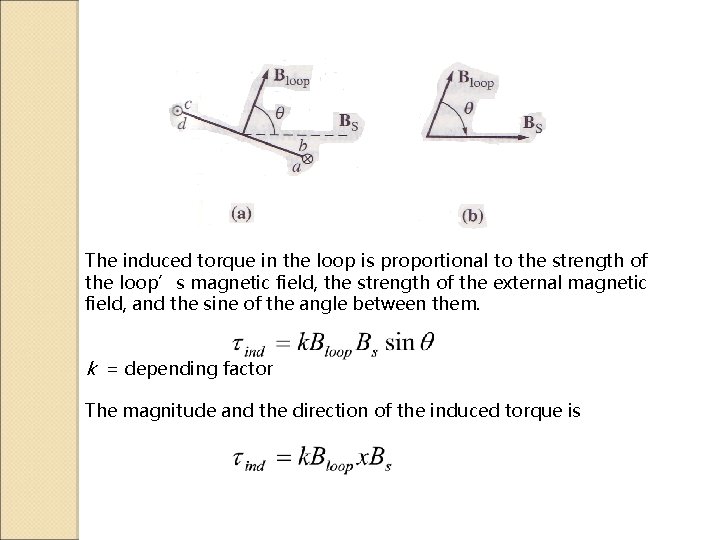
The induced torque in the loop is proportional to the strength of the loop’s magnetic field, the strength of the external magnetic field, and the sine of the angle between them. k = depending factor The magnitude and the direction of the induced torque is

Concept: Induced Torque in AC machine “ If a current flows in the loop, then a torque will be induced on the wire loop. ” Induced torque is expressed as,

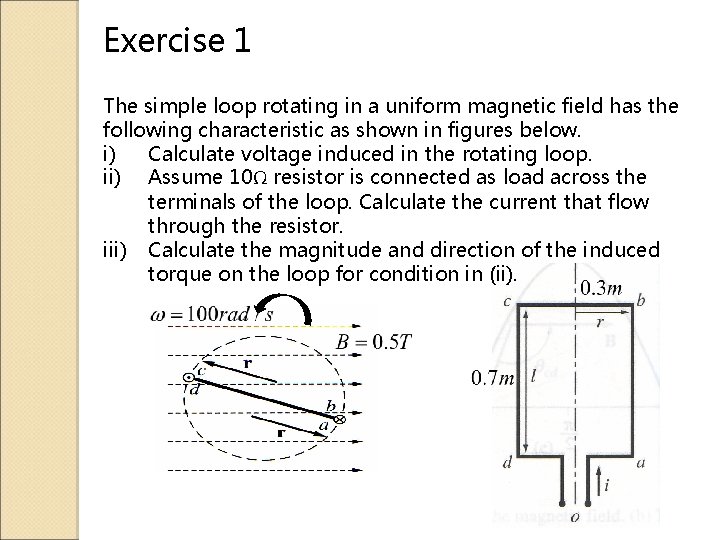
Exercise 1 The simple loop rotating in a uniform magnetic field has the following characteristic as shown in figures below. i) Calculate voltage induced in the rotating loop. ii) Assume 10Ω resistor is connected as load across the terminals of the loop. Calculate the current that flow through the resistor. iii) Calculate the magnitude and direction of the induced torque on the loop for condition in (ii).

Solution (i) (iii)

Power Flows & Losses �AC generators take in mechanical power and produce electric power, while AC motors take in electric power and produce mechanical power. �In both cases, not all the power input to the machine appears in useful form at the other end; there is always some loss associated to the process.

Efficiency of AC Machine � Given as � The difference between the input power and the output power of a machine is the losses

�Losses that occur in AC machines can be divided into four basic categories: - 1) 2) 3) 4) Electrical/copper losses (I 2 R) Core Losses Mechanical Losses Stray Load Losses

�Electrical/Copper Losses ◦ Resistive heating losses that occur in the stator and the rotor windings of the machine. ◦ Stator copper losses equation are given as, ◦ Rotor copper losses equation are given as,

�Core losses ◦ Hysteresis and eddy current losses which occur in the metal of the motor. ◦ These losses vary as square of the flux density (B 2), and for stator, as the 1. 5 th power of the speed of rotation of the magnetic fields (n 1. 5) �Mechanical Losses ◦ Losses associated with the mechanical effects. ◦ Friction- caused by the friction of bearings in the machine ◦ Windage – caused by friction between the moving parts of the machine and the air inside the motor’s casing Ø Typically, mechanical and core losses are always lumped together and called no-load rotational loss of machine. At no load, all the input power must be used to overcome these losses. Therefore, measuring the input power to the stator at no load (machine acts as motor), will give the approximate value of these losses.

�Stray losses ◦ No matter how careful losses are accounted for, some always escape inclusion in one of the categories discussed ealier. ◦ Most machine, stray losses are taken by convention to be 1% of full load.

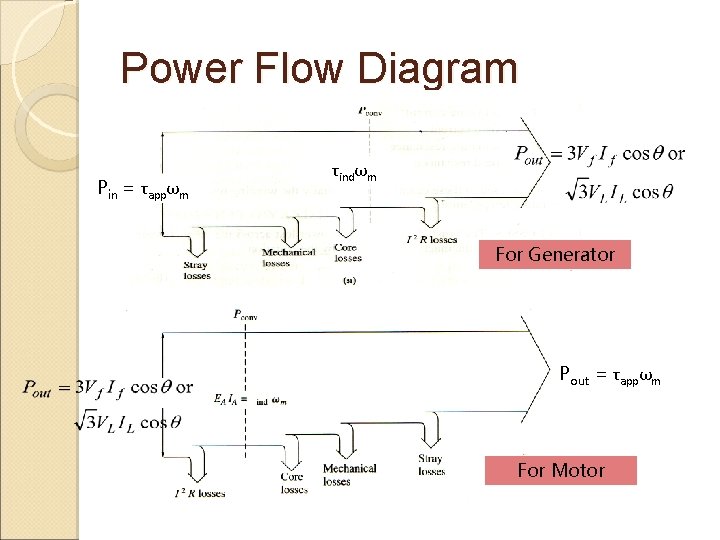
Power Flow Diagram Pin = τappωm τindωm For Generator Pout = τappωm For Motor

Voltage Regulation � Voltage Regulation (VR) – measure the ability of a generator to keep a constant voltage at its terminals as load varies. � It is a rough measure of the shape of the generator’s voltage-current characteristic. ◦ Positive VR: drooping characteristic ◦ Negative VR: rising characteristic � Small VR is better in the sense that voltage at the terminals of the generator is more constant with the variations in load.

Speed Regulation � Speed Regulation (SR) – measure the ability of a motor to keep constant shaft speed as load varies. � Defined as, � It is a rough measure of the shape of a motor’s torque-speed characteristic. ◦ Positive SR: speed drops with increasing of load ◦ Negative SR: speed increases with increasing of load