Chapter 37 The Normal Probability Distribution rights 2010

Section 7. 3 Applications of the Normal Distribution © 2010 Pearson Prentice Hall. All

© 2010 Pearson Prentice Hall. All rights reserved 7 -3

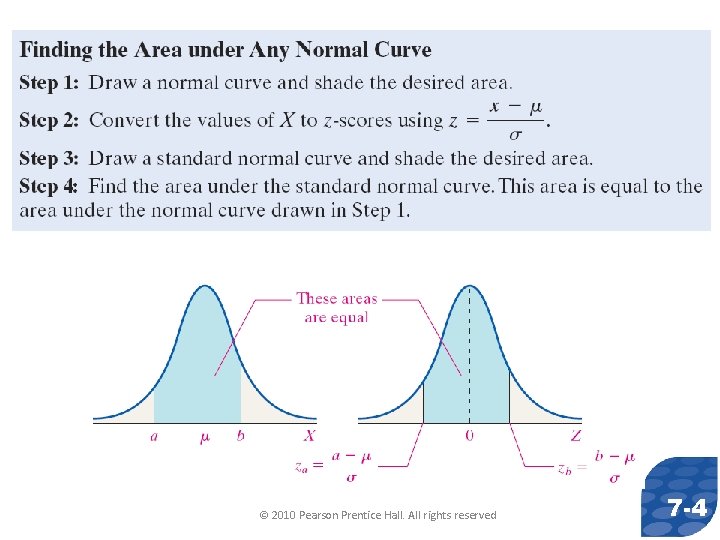
© 2010 Pearson Prentice Hall. All rights reserved 7 -4

EXAMPLE Finding the Probability of a Normal Random Variable It is known that the length of a certain steel rod is normally distributed with a mean of 100 cm and a standard deviation of 0. 45 cm. * What is the probability that a randomly selected steel rod has a length less than 99. 2 cm? Interpretation: If we randomly selected 100 steel rods, we would expect about 4 of them to be less than 99. 2 cm. *Based upon information obtained from Stefan Wilk. © 2010 Pearson Prentice Hall. All rights reserved 7 -5

EXAMPLE Finding the Probability of a Normal Random Variable It is known that the length of a certain steel rod is normally distributed with a mean of 100 cm and a standard deviation of 0. 45 cm. What is the probability that a randomly selected steel rod has a length between 99. 8 and 100. 3 cm? Interpretation: If we randomly selected 100 steel rods, we would expect about 42 of them to be between 99. 8 cm and 100. 3 cm. © 2010 Pearson Prentice Hall. All rights reserved 7 -6

EXAMPLE Finding the Percentile Rank of a Normal Random Variable The combined (verbal + quantitative reasoning) score on the GRE is normally distributed with mean 1049 and standard deviation 189. (Source: http: //www. ets. org/Media/Tests/GRE/pdf/994994. pdf. ) The Department of Psychology at Columbia University in New York requires a minimum combined score of 1200 for admission to their doctoral program. (Source: www. columbia. edu/cu/gsas/departments/psychology/department. html. ) What is the percentile rank of a student who earns a combined GRE score of 1300? The area under the normal curve is a probability, proportion, or percentile. Here, the area under the normal curve to the left of 1300 represents the percentile rank of the student. Area left of 1300 = Area left of (z = 1. 33) = 0. 91 (rounded to two decimal places) Interpretation: The student scored at the 91 st percentile. This means the student scored better than 91% of the students who took the GRE. 7 -7 © 2010 Pearson Prentice Hall. All rights reserved

EXAMPLE Finding the Proportion Corresponding to a Normal Random Variable It is known that the length of a certain steel rod is normally distributed with a mean of 100 cm and a standard deviation of 0. 45 cm. Suppose the manufacturer must discard all rods less than 99. 1 cm or longer than 100. 9 cm. What proportion of rods must be discarded? The proportion is the area under the normal curve to the left of 99. 1 cm plus the area under the normal curve to the right of 100. 9 cm. Area left of 99. 1 + area right of 100. 9 = (Area left of z = -2) + (Area right of z = 2) = 0. 0228 + 0. 0228 = 0. 0456 Interpretation: The proportion of rods that must be discarded is 0. 0456. If the company manufactured 1000 rods, they would expect to discard about 46 of them. © 2010 Pearson Prentice Hall. All rights reserved 7 -8

© 2010 Pearson Prentice Hall. All rights reserved 7 -9

© 2010 Pearson Prentice Hall. All rights reserved 7 -10

EXAMPLE Finding the Value of a Normal Random Variable The combined (verbal + quantitative reasoning) score on the GRE is normally distributed with mean 1049 and standard deviation 189. (Source: http: //www. ets. org/Media/Tests/GRE/pdf/994994. pdf. ) What is the score of a student whose percentile rank is at the 85 th percentile? The z-score that corresponds to the 85 th percentile is the z-score such that the area under the standard normal curve to the left is 0. 85. This z-score is 1. 04. x = µ + zσ = 1049 + 1. 04(189) = 1246 Interpretation: The proportion of rods that must be discarded is 0. 0456. If the company manufactured 1000 rods, they would expect to discard about 46 of them. © 2010 Pearson Prentice Hall. All rights reserved 7 -11

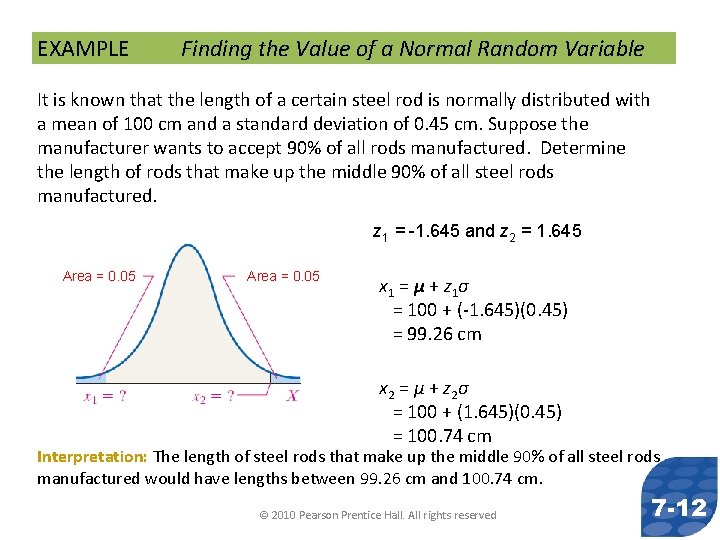
EXAMPLE Finding the Value of a Normal Random Variable It is known that the length of a certain steel rod is normally distributed with a mean of 100 cm and a standard deviation of 0. 45 cm. Suppose the manufacturer wants to accept 90% of all rods manufactured. Determine the length of rods that make up the middle 90% of all steel rods manufactured. z 1 = -1. 645 and z 2 = 1. 645 Area = 0. 05 x 1 = µ + z 1 σ = 100 + (-1. 645)(0. 45) = 99. 26 cm x 2 = µ + z 2 σ = 100 + (1. 645)(0. 45) = 100. 74 cm Interpretation: The length of steel rods that make up the middle 90% of all steel rods manufactured would have lengths between 99. 26 cm and 100. 74 cm. © 2010 Pearson Prentice Hall. All rights reserved 7 -12