Chapter 3 Workforce scheduling Plan Introduction Daysoff scheduling

Chapter 3 Workforce scheduling

Plan • Introduction • Days-off scheduling • Shift scheduling • Cyclic staffing probme • Crew scheduling -2 -

Intoduction • Workforce allocation & personnel scheduling deal with the arrangement of work schedules and the assignment of personnel to shits to cover the demand for resources that vary over time. • In service environments the operations are often prolonged and irregular, and the staff requirements fluctuate over time. • The schedules are typically subject to various constraints dictated by equipment requirements, union rules, . . . -3 -

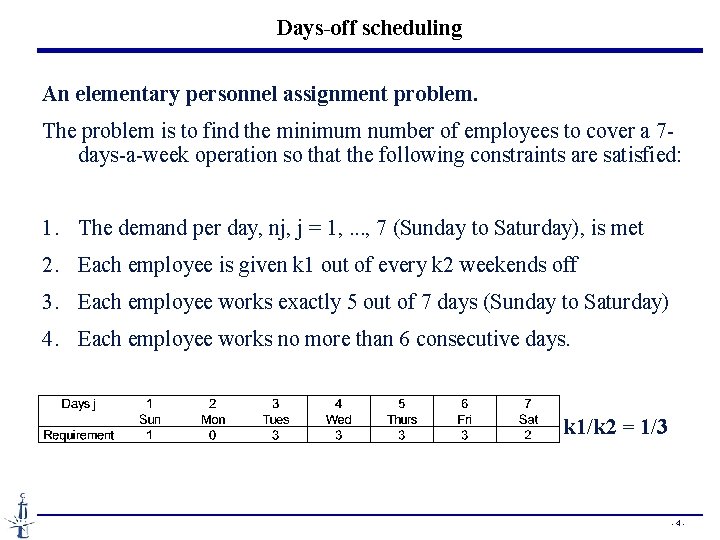
Days-off scheduling An elementary personnel assignment problem. The problem is to find the minimum number of employees to cover a 7 days-a-week operation so that the following constraints are satisfied: 1. The demand per day, nj, j = 1, . . . , 7 (Sunday to Saturday), is met 2. Each employee is given k 1 out of every k 2 weekends off 3. Each employee works exactly 5 out of 7 days (Sunday to Saturday) 4. Each employee works no more than 6 consecutive days. k 1/k 2 = 1/3 -4 -

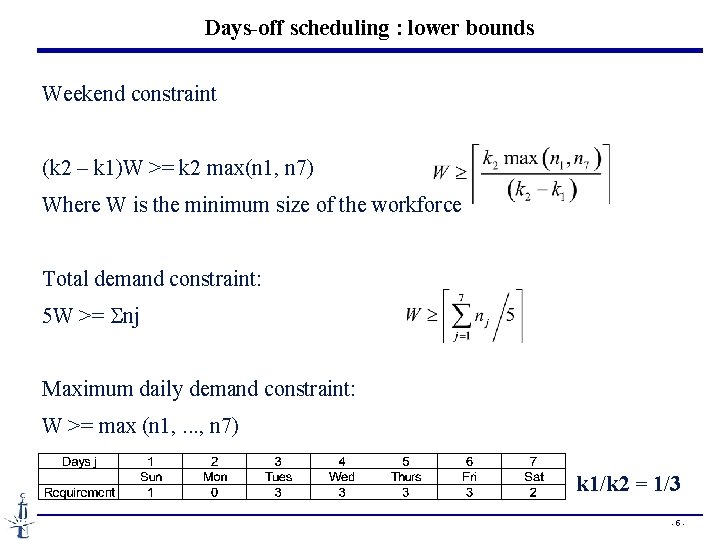
Days-off scheduling : lower bounds Weekend constraint (k 2 – k 1)W >= k 2 max(n 1, n 7) Where W is the minimum size of the workforce Total demand constraint: 5 W >= Snj Maximum daily demand constraint: W >= max (n 1, . . . , n 7) k 1/k 2 = 1/3 -5 -

Days-off scheduling : Algorithm W = min workforce, n = max(n 1, n 7) Step 1. (Schedule the weekends off) Assign the 1 st weekend off to the first W-n employees Assign the 2 nd weekend off to the second W-n employees This process is continued cyclically. k 1/k 2 = 1/3 -6 -

Days-off scheduling : Algorithm uj = W- nj, j= 2, . . . , 6, uj = n – nj, j = 1, 7 Step 2. (Determine the additional off-day pairs) Construct a list of n pairs of off days, numbered 1 to n. Choose day k such that uk = max(u 1, . . . , u 7) Choose day l (l k), such that ul > 0; if ul = 0 for all l k, set l = k Add the pair (k, l) to the list and decrease uk and ul by 1. Repeat the process n times. (2, 1), Sunday-Monday (2, 2), Monday-Monday (non distinct pairs) Remaining offs 3 -1 -1 W – demand – existing offs k 1/k 2 = 1/3 -7 -

Days-off scheduling : Algorithm Set i = 1 Step 3. (Categorize emplyees in week i) Type T 1 : weekend i off, no days needed during week i, weekend i+1 off Type T 2 : weekend i off, 1 off day needed during week i, weekend i+1 on Type T 3 : weekend i on, 1 off day needed during week i, weekend i+1 off Type T 4 : weekend i on, 2 off days needed during week i, weekend i+1 on |T 3| + |T 4| = n, |T 2| + |T 4| = n (as n people working each weekend) Pair Each employee of T 2 with one of T 3 Step 4 (Assign off-day pairs in week i) Assign the n pairs of days, starting from the top off the list as follows: First assign pairs of days to the employees of T 4 Then, to each employee of T 3 and his companion of T 2, assign the one of T 3 the earliest day of the pair. Set i = i+1 and return to step 3. -8 -

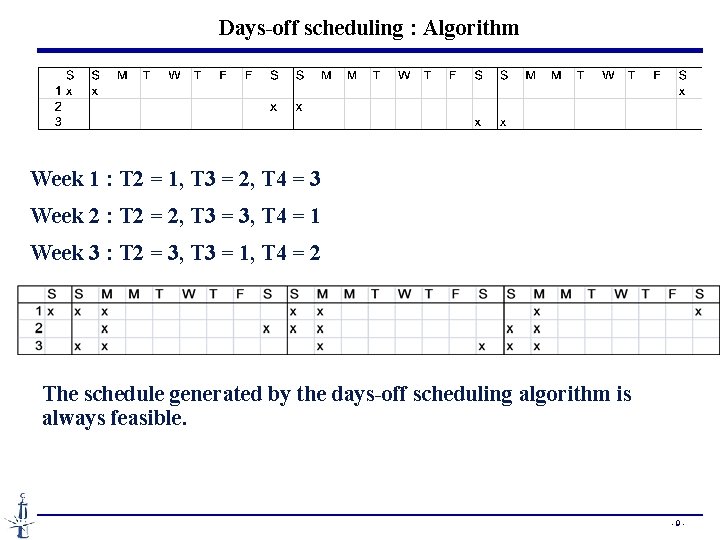
Days-off scheduling : Algorithm Week 1 : T 2 = 1, T 3 = 2, T 4 = 3 Week 2 : T 2 = 2, T 3 = 3, T 4 = 1 Week 3 : T 2 = 3, T 3 = 1, T 4 = 2 The schedule generated by the days-off scheduling algorithm is always feasible. -9 -

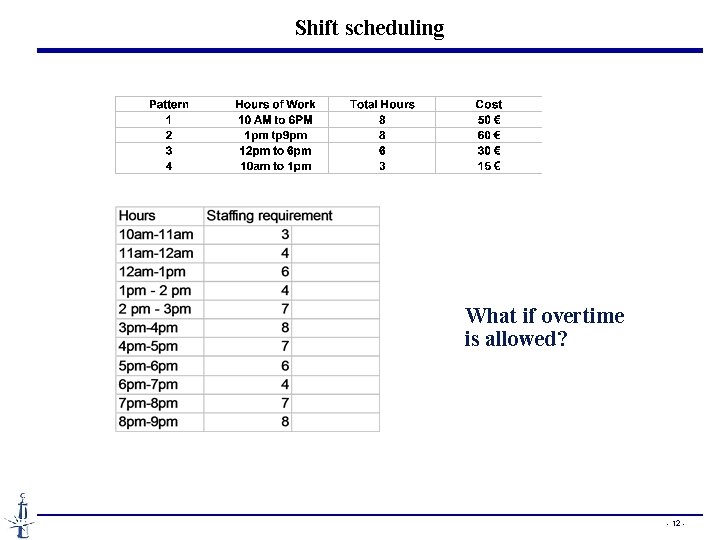
Shift scheduling A cycle (one day, one or several weeks) is fixed. Each work assignment pattern over a cycle has its own cost. Problem: m time intervals/periods in the predetermined cycle bi personnel are required for period i b different shift patterns, and each employee is assigned to one and only one pattern (a 1 j, a 2 j, . . . , amj) = shift pattern j with aij = 1 if period i is a work period. cj = cost of patern j Determine the number of employees of each pattern in order to minimise the total cost. - 10 -

Shift scheduling - 11 -

Shift scheduling What if overtime is allowed? - 12 -

Shift scheduling • The integer programming formulation of the general personnel scheduling problem (with arbitrary 0 -1 A matrix) is NP-hard • The special case with each column containing a contiguous set of ones is easy and the solution of the LP-relaxation is always integer. - 13 -

Cyclic staffing problem The objective is to minimise the cost of assigning people to an m-period cyclic schedule so that sufficient workers are present during time period i, in order to meet requirement bi, and each person works a shift of k consecutive periods and is free the other m-k periods. Each column is a possible shift (5, 7) cyclic staffing - 14 -

Cyclic staffing problem : algorithm Step 1. Solve the linear relaxation of the problem to obtain xi’ If (xi’) are integer, STOP Step 2. Form two linear programs LP’ and LP’’ from the relaxation of the original problem by adding respectively the constraints: LP’’ has an optimal solution that is integer If LP’ does not have a feaible solution, then the solution of LP’’ is the optimal solution If LP’ has a feasible solution, then it has an optimal solution that is integer and the best of LP’ and LP’’ solutions is the optimal solution. - 15 -

Cyclic staffing problem : algorithm - 16 -

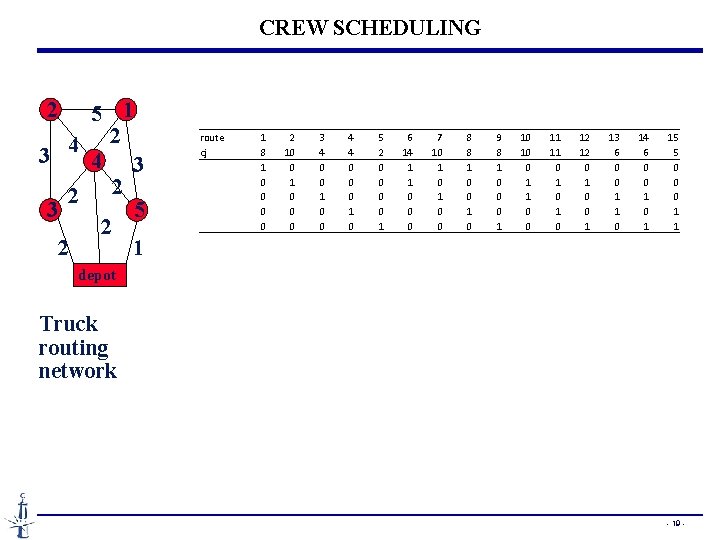
CREW SCHEDULING • Crew scheduling problems are very important in transportation especially in airline industry • Consider a set of m jobs, or flight legs. • A flight leg is characterized by a point of departure and a point of arrival, as well as an approximate time interval during which the flight has to take place. • There is a set of n feasible and permissible combinations of flight legs that one crew can handle, round trips or tours. • Each round trip j, has a cost cj. • Crew schedule determines round trips to select in order to minimize the total cost under the constraint that each flight leg is covered exactly once by one and only one round trip. - 17 -

CREW SCHEDULING • Each column in the A matrix is a round trip, and each row is a flight leg that must be covered exactly once by one round trip. • Set partitioning problem. - 18 -

CREW SCHEDULING 2 5 1 2 4 3 2 2 3 5 2 2 1 route cj 1 8 1 0 0 2 10 0 1 0 0 0 3 4 0 0 1 0 0 4 4 0 0 0 1 0 5 2 0 0 1 6 14 1 1 0 0 0 7 10 1 0 0 8 8 1 0 0 1 0 9 8 1 0 0 0 1 10 10 0 1 1 0 0 11 11 0 1 0 12 12 0 1 0 0 1 13 6 0 0 1 1 0 14 6 0 0 1 15 5 0 0 0 1 1 depot Truck routing network - 19 -