Chapter 3 VLSI Subsystem Design JinFu Li Advanced

Chapter 3 VLSI Subsystem Design Jin-Fu Li Advanced Reliable Systems (ARES) Laboratory Department of Electrical Engineering National Central University Jhongli, Taiwan

Outline Introduction Datapath Operators Control Structures Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 2

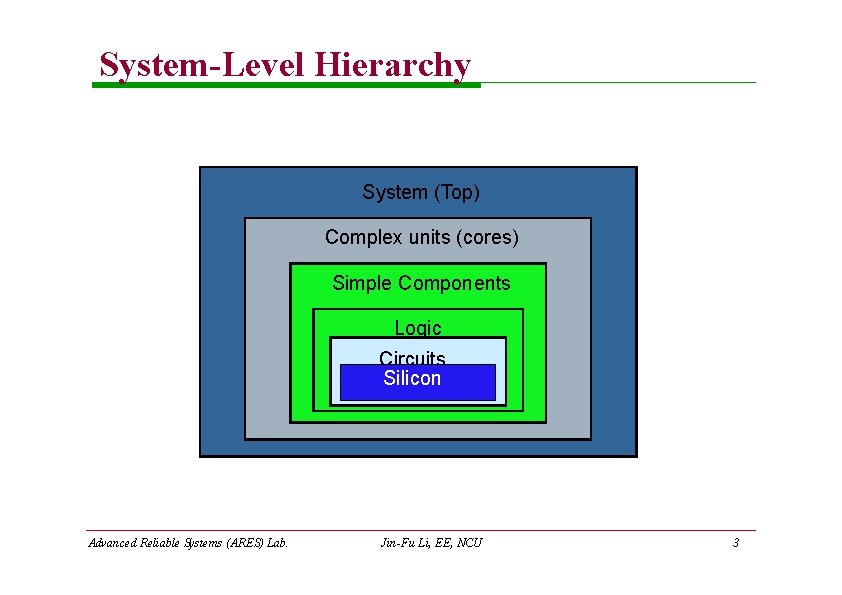
System-Level Hierarchy System (Top) Complex units (cores) Simple Components Logic Circuits Silicon Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 3

Categories of Components Types of digital component Datapath operators Memory elements Control structures I/O cells Tradeoff of selection Speed Density Programmability Easy of design etc Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 4

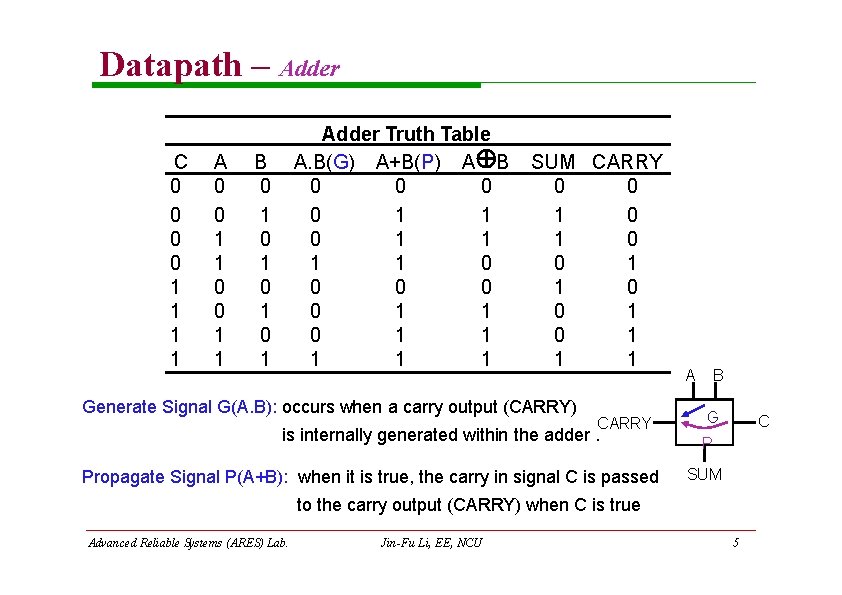
Datapath – Adder C 0 0 1 1 Adder Truth Table A. B(G) A+B(P) A B 0 0 1 1 0 0 0 1 1 1 1 1 B 0 1 0 1 SUM CARRY 0 0 1 1 0 0 1 1 1 Generate Signal G(A. B): occurs when a carry output (CARRY) CARRY is internally generated within the adder. Propagate Signal P(A+B): when it is true, the carry in signal C is passed A B G C P SUM to the carry output (CARRY) when C is true Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 5

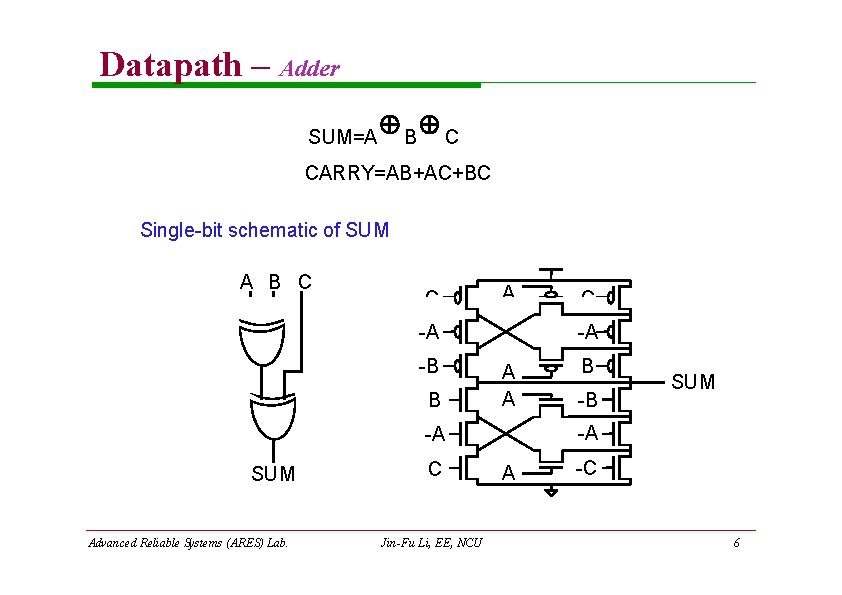
Datapath – Adder SUM=A B C CARRY=AB+AC+BC Single-bit schematic of SUM A B C -C A -A -B B -A A A Advanced Reliable Systems (ARES) Lab. C Jin-Fu Li, EE, NCU B -B SUM -A -A SUM C A -C 6

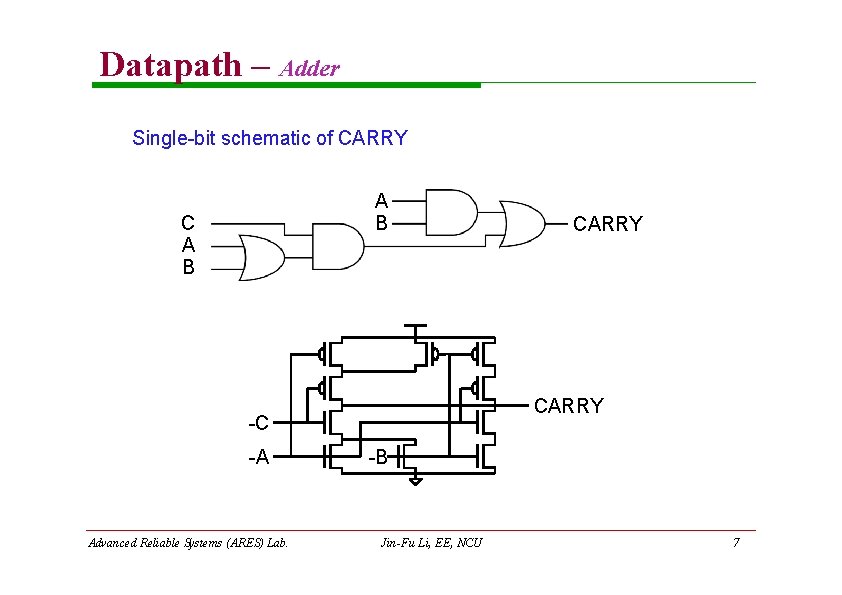
Datapath – Adder Single-bit schematic of CARRY A B CARRY -C -A Advanced Reliable Systems (ARES) Lab. CARRY -B Jin-Fu Li, EE, NCU 7

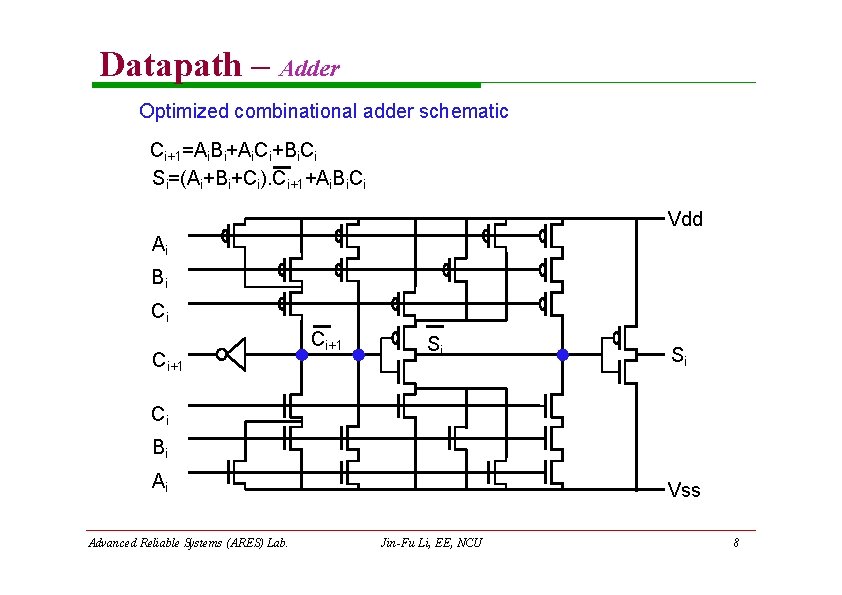
Datapath – Adder Optimized combinational adder schematic Ci+1=Ai. Bi+Ai. Ci+Bi. Ci Si=(Ai+Bi+Ci). Ci+1+Ai. Bi. Ci Vdd Ai Bi Ci Ci+1 Si Si Ci Bi Ai Advanced Reliable Systems (ARES) Lab. Vss Jin-Fu Li, EE, NCU 8

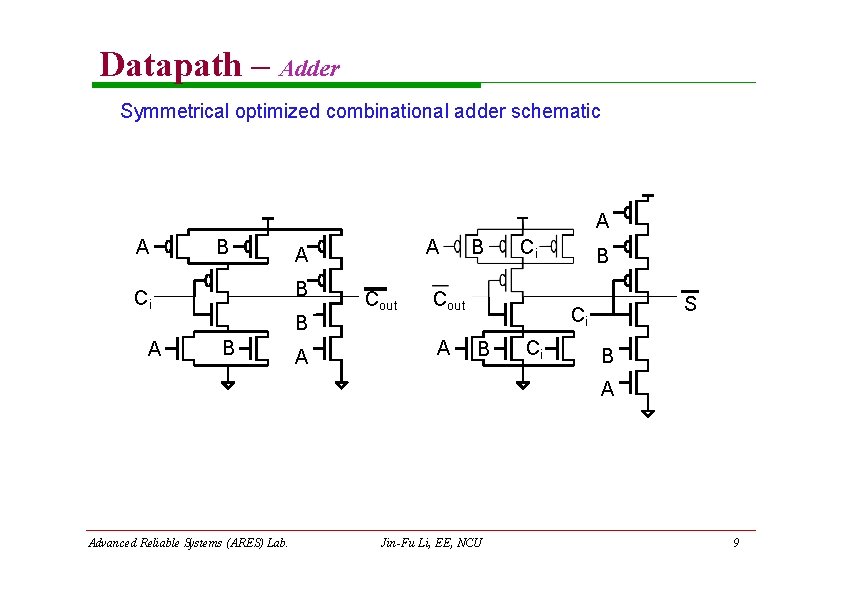
Datapath – Adder Symmetrical optimized combinational adder schematic A A B B Ci B A A A Cout B Ci Cout A B S Ci B A Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 9

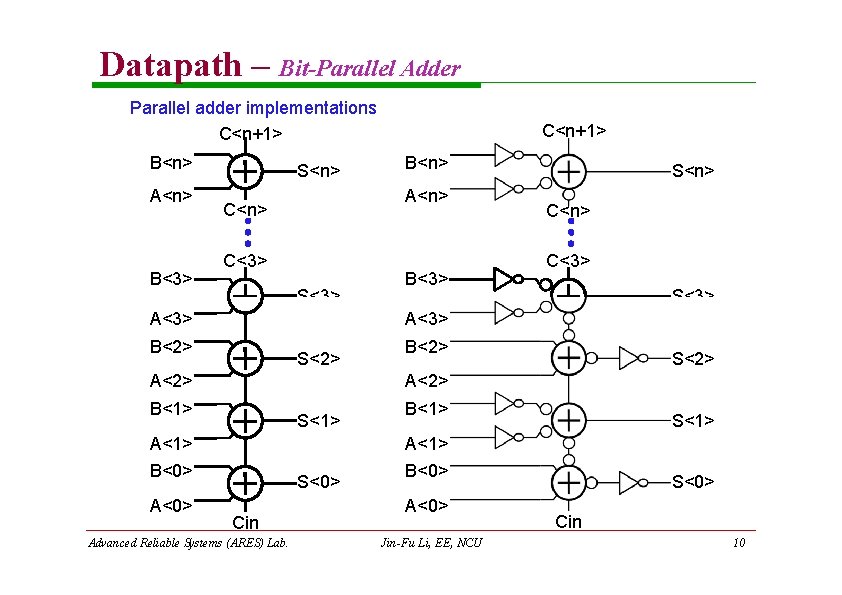
Datapath – Bit-Parallel Adder Parallel adder implementations C<n+1> B<n> A<n> B<3> S<n> B<n> A<n> C<3> S<3> A<3> B<3> S<n> C<3> S<3> A<3> B<2> S<2> A<2> B<1> S<1> A<1> B<0> A<0> C<n+1> S<0> Cin Advanced Reliable Systems (ARES) Lab. B<1> S<1> A<1> B<0> A<0> Jin-Fu Li, EE, NCU S<0> Cin 10

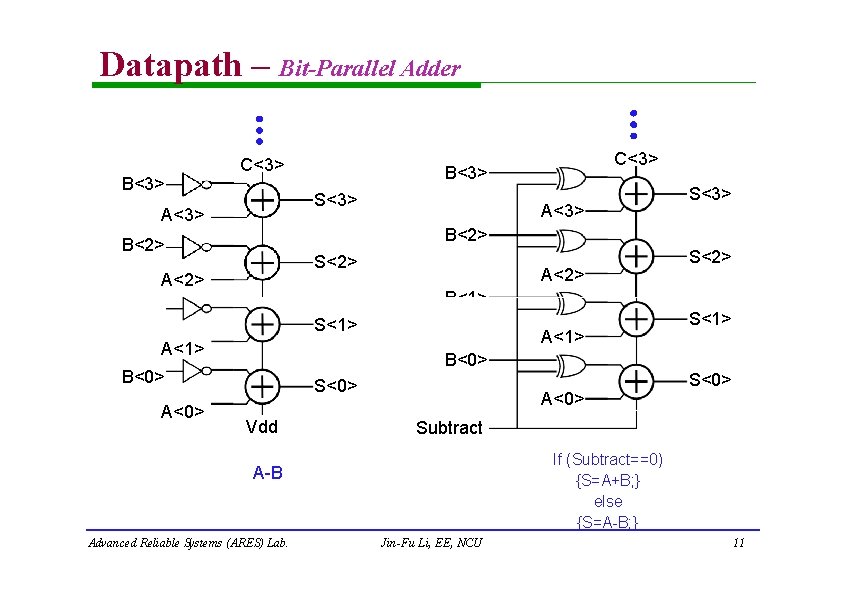
Datapath – Bit-Parallel Adder B<3> C<3> S<3> A<3> S<3> B<2> S<2> A<2> B<1> A<2> S<2> B<1> S<1> A<1> B<0> A<0> C<3> B<3> S<0> Vdd A<0> Subtract If (Subtract==0) {S=A+B; } else {S=A-B; } A-B Advanced Reliable Systems (ARES) Lab. S<1> Jin-Fu Li, EE, NCU 11

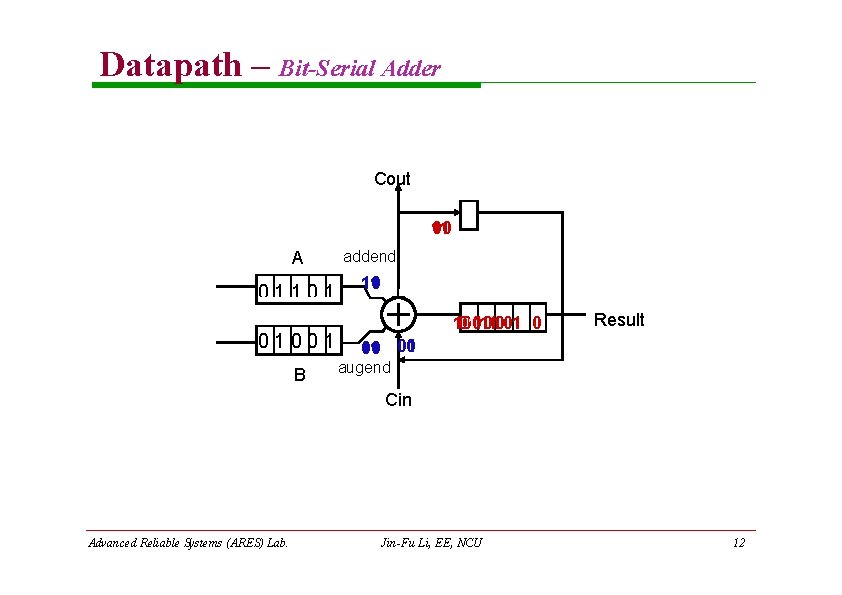
Datapath – Bit-Serial Adder Cout 1 010 A 01101 01001 B addend 110 10010 11011001 0 Result 1 010 001 augend Cin Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 12

Datapath – Carry Look-Ahead Adder (CLA) Objective To avoid the linear growth of the carry delay, we use a Carry Look-Ahead Adder (CLA) in which the carries can be generated in parallel Feature The Carry of each bit is generated from the propagate and the generate signals as well as the input carry The propagate and the generate signals are derived from the operand Ai and Bi by Gi=Ai. Bi Pi=Ai+Bi Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 13

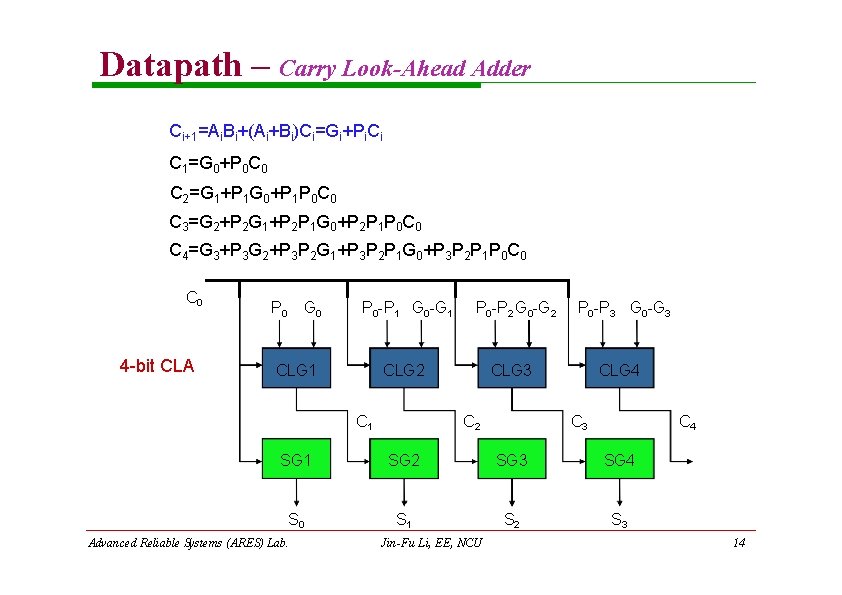
Datapath – Carry Look-Ahead Adder Ci+1=Ai. Bi+(Ai+Bi)Ci=Gi+Pi. Ci C 1=G 0+P 0 C 0 C 2=G 1+P 1 G 0+P 1 P 0 C 0 C 3=G 2+P 2 G 1+P 2 P 1 G 0+P 2 P 1 P 0 C 0 C 4=G 3+P 3 G 2+P 3 P 2 G 1+P 3 P 2 P 1 G 0+P 3 P 2 P 1 P 0 C 0 4 -bit CLA P 0 G 0 P 0 -P 1 G 0 -G 1 P 0 -P 2 G 0 -G 2 CLG 3 CLG 1 C 2 P 0 -P 3 G 0 -G 3 CLG 4 C 3 C 4 SG 1 SG 2 SG 3 SG 4 S 0 S 1 S 2 S 3 Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 14

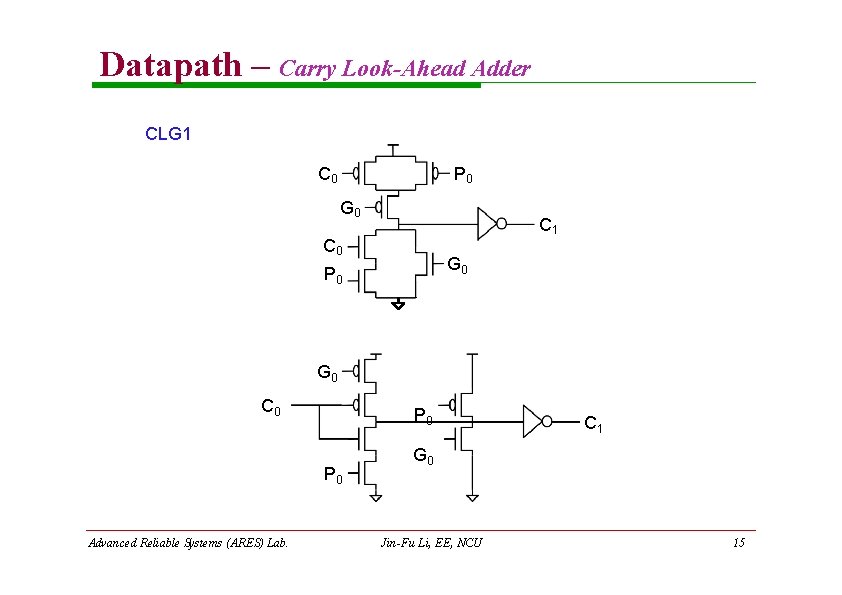
Datapath – Carry Look-Ahead Adder CLG 1 C 0 P 0 G 0 C 1 C 0 G 0 P 0 G 0 C 0 P 0 Advanced Reliable Systems (ARES) Lab. C 1 G 0 Jin-Fu Li, EE, NCU 15

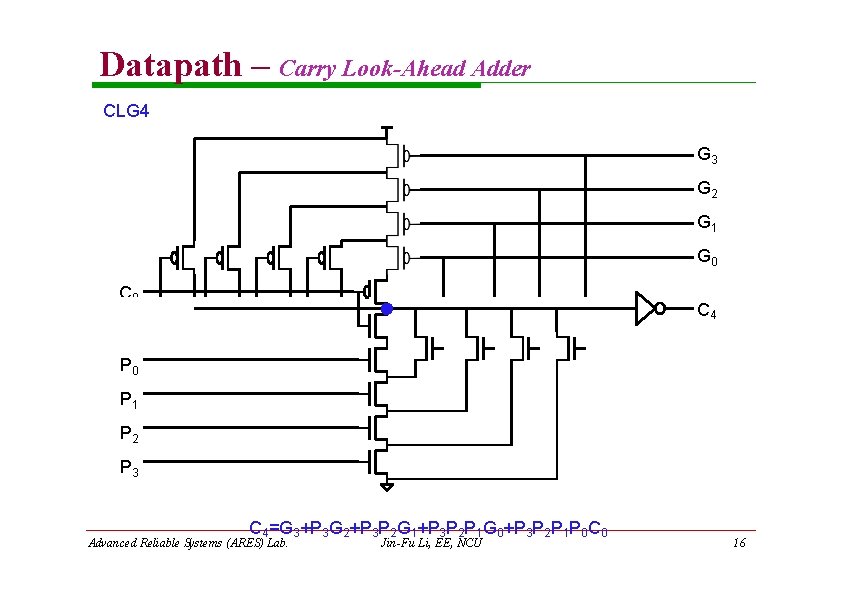
Datapath – Carry Look-Ahead Adder CLG 4 G 3 G 2 G 1 G 0 C 4 P 0 P 1 P 2 P 3 C 4=G 3+P 3 G 2+P 3 P 2 G 1+P 3 P 2 P 1 G 0+P 3 P 2 P 1 P 0 C 0 Jin-Fu Li, EE, NCU Advanced Reliable Systems (ARES) Lab. 16

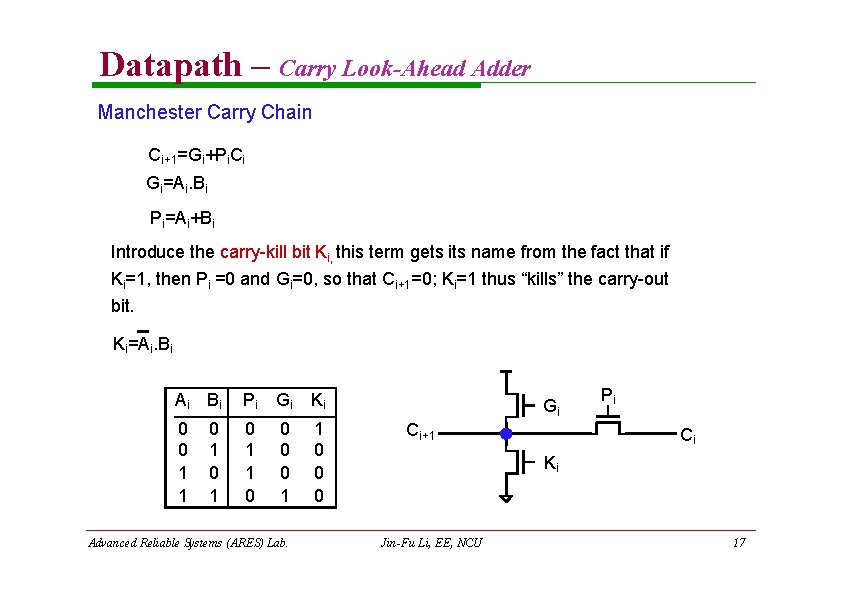
Datapath – Carry Look-Ahead Adder Manchester Carry Chain Ci+1=Gi+Pi. Ci Gi=Ai. Bi Pi=Ai+Bi Introduce the carry-kill bit Ki, this term gets its name from the fact that if Ki=1, then Pi =0 and Gi=0, so that Ci+1=0; Ki=1 thus “kills” the carry-out bit. Ki=Ai. Bi Ai Bi Pi Gi Ki 0 0 1 1 0 0 1 0 1 Advanced Reliable Systems (ARES) Lab. Gi Ci+1 Pi Ci Ki Jin-Fu Li, EE, NCU 17

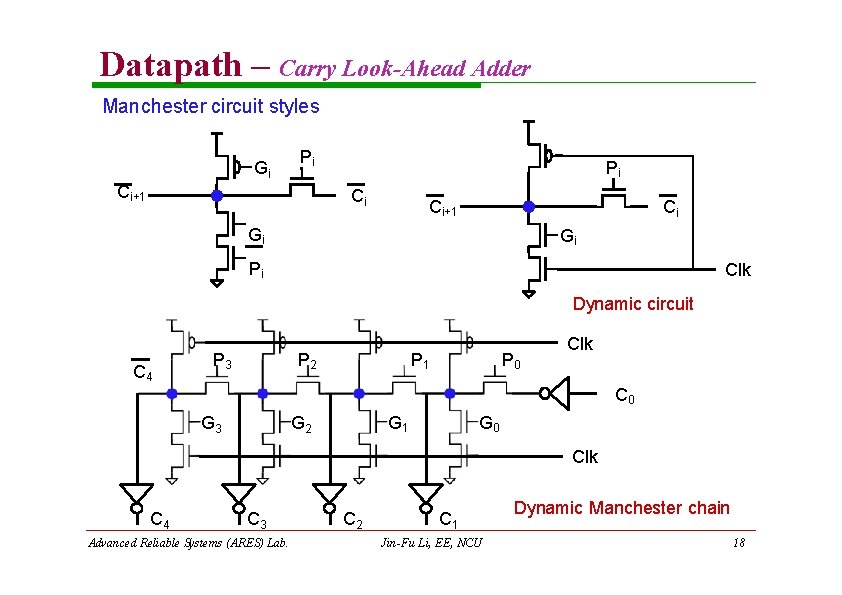
Datapath – Carry Look-Ahead Adder Manchester circuit styles Gi Pi Ci+1 Pi Ci Ci+1 Ci Gi Gi Pi Clk Dynamic circuit Static circuit C 4 P 3 P 0 P 1 P 2 Clk C 0 G 1 G 2 G 3 Clk C 4 C 3 Advanced Reliable Systems (ARES) Lab. C 2 C 1 Jin-Fu Li, EE, NCU Dynamic Manchester chain 18

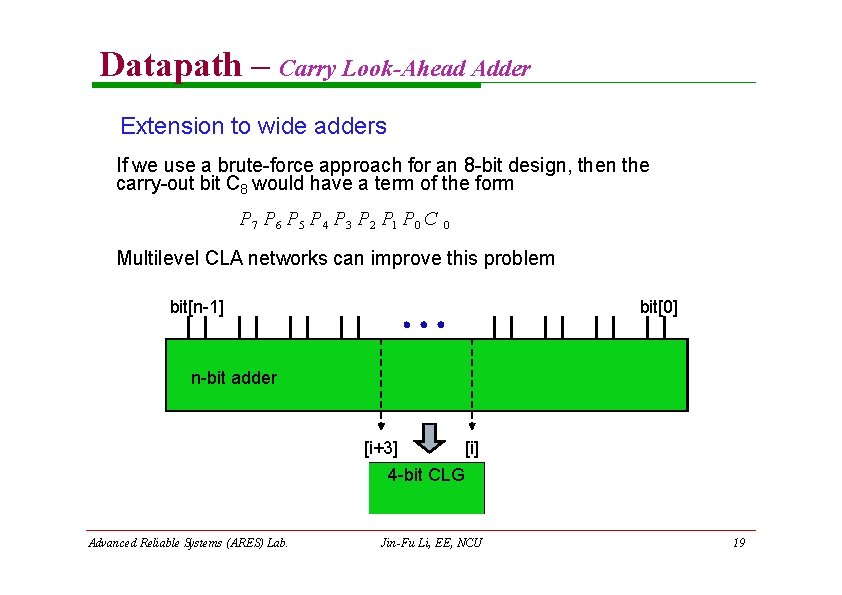
Datapath – Carry Look-Ahead Adder Extension to wide adders If we use a brute-force approach for an 8 -bit design, then the carry-out bit C 8 would have a term of the form P 7 P 6 P 5 P 4 P 3 P 2 P 1 P 0 C 0 Multilevel CLA networks can improve this problem bit[n-1] bit[0] n-bit adder [i+3] [i] 4 -bit CLG Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 19

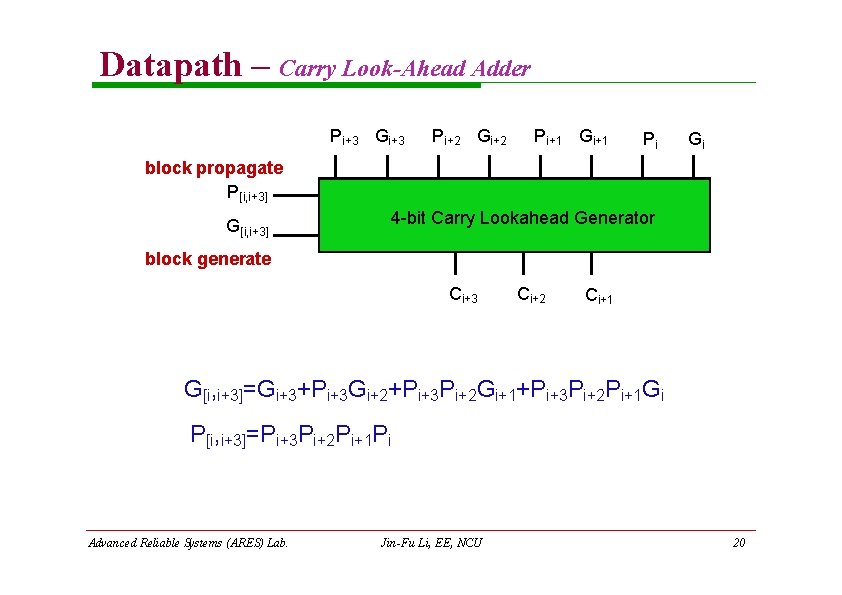
Datapath – Carry Look-Ahead Adder Pi+3 Gi+3 Pi+2 Gi+2 Pi+1 Gi+1 Pi Gi block propagate P[i, i+3] G[i, i+3] 4 -bit Carry Lookahead Generator block generate Ci+3 Ci+2 Ci+1 G[i, i+3]=Gi+3+Pi+3 Gi+2+Pi+3 Pi+2 Gi+1+Pi+3 Pi+2 Pi+1 Gi P[i, i+3]=Pi+3 Pi+2 Pi+1 Pi Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 20

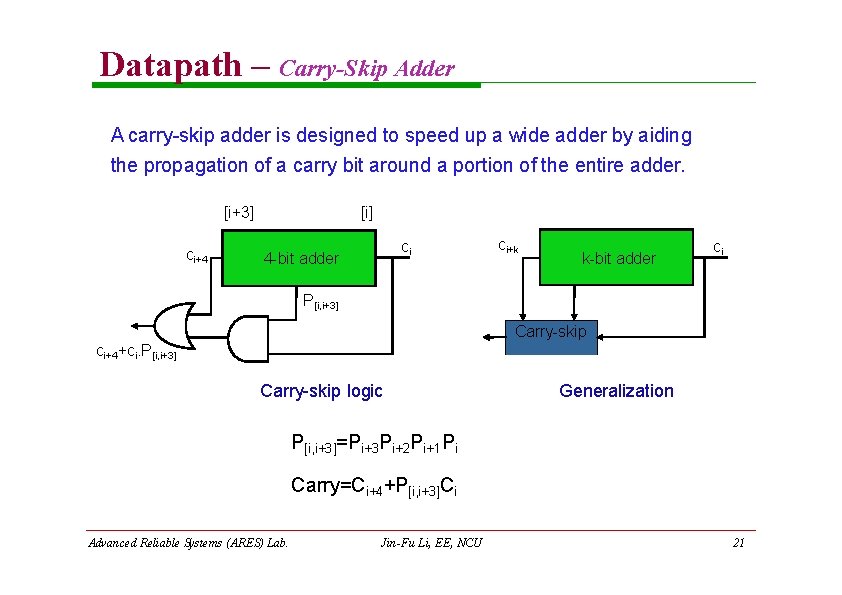
Datapath – Carry-Skip Adder A carry-skip adder is designed to speed up a wide adder by aiding the propagation of a carry bit around a portion of the entire adder. [i+3] ci+4 [i] ci 4 -bit adder ci+k k-bit adder ci P[i, i+3] Carry-skip ci+4+ci. P[i, i+3] Carry-skip logic Generalization P[i, i+3]=Pi+3 Pi+2 Pi+1 Pi Carry=Ci+4+P[i, i+3]Ci Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 21

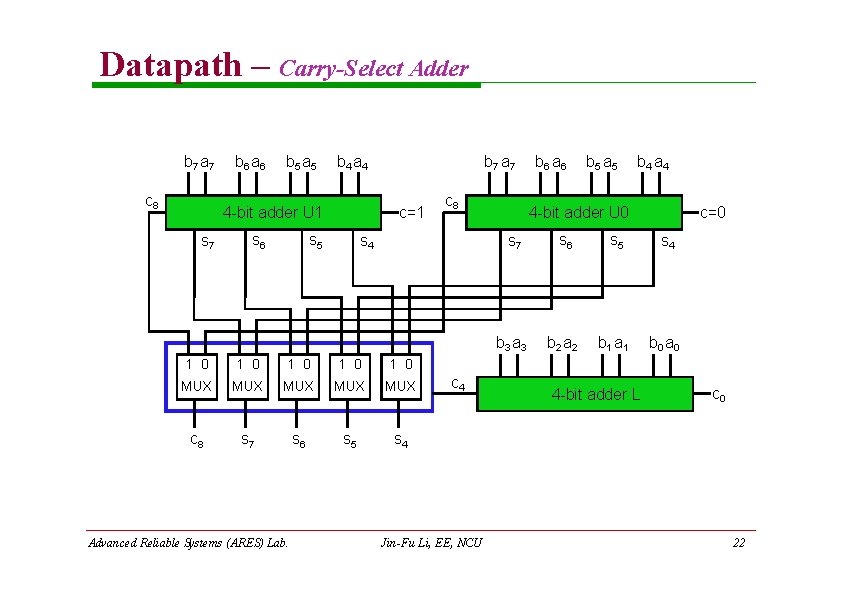
Datapath – Carry-Select Adder b 7 a 7 c 8 b 6 a 6 b 5 a 5 b 4 a 4 c=1 4 -bit adder U 1 s 7 s 6 b 7 a 7 s 5 s 4 1 0 1 0 1 0 MUX MUX MUX c 8 s 7 s 6 s 5 s 4 Advanced Reliable Systems (ARES) Lab. c 8 c 4 Jin-Fu Li, EE, NCU b 6 a 6 b 5 a 5 b 4 a 4 c=0 4 -bit adder U 0 s 7 s 6 s 5 s 4 b 3 a 3 b 2 a 2 b 1 a 1 b 0 a 0 4 -bit adder L c 0 22

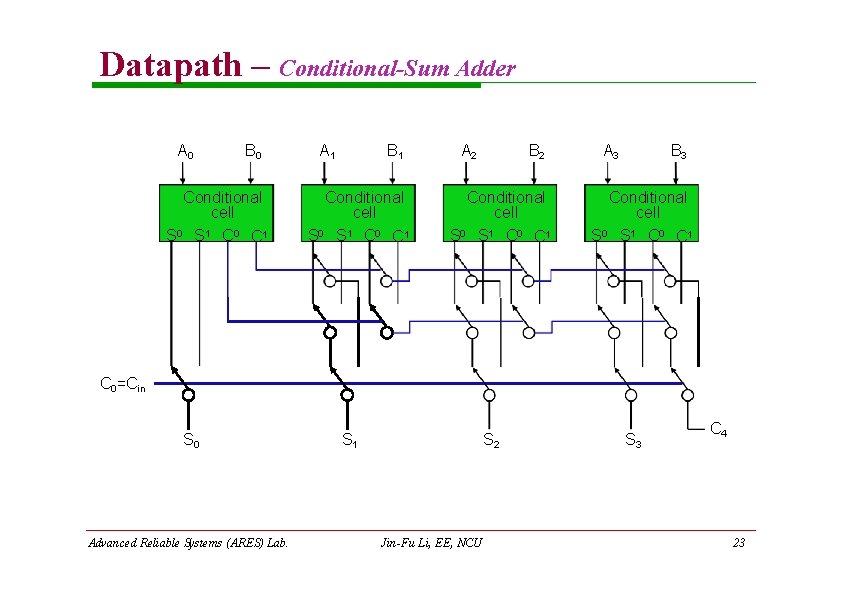
Datapath – Conditional-Sum Adder A 0 B 0 Conditional cell S 0 S 1 C 0 C 1 A 1 B 1 Conditional cell S 0 S 1 C 0 C 1 A 2 B 2 Conditional cell S 0 S 1 C 0 C 1 A 3 B 3 Conditional cell S 0 S 1 C 0 C 1 C 0=Cin S 0 Advanced Reliable Systems (ARES) Lab. S 1 S 2 Jin-Fu Li, EE, NCU S 3 C 4 23

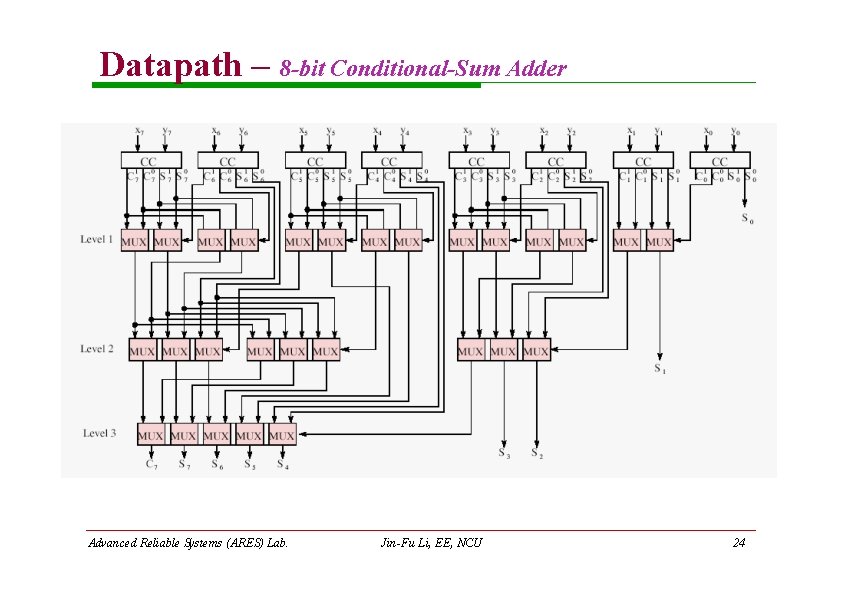
Datapath – 8 -bit Conditional-Sum Adder Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 24

Datapath – Multipliers Bit-level multiplier a b 0 0 1 1 axb 0 1 0 0 0 1 a b axb Multiplication of two 4 -bit words p 7 a 3 b 3 a 3 b 2 a 2 b 3 p 6 p 5 Advanced Reliable Systems (ARES) Lab. a 3 b 3 a 2 b 2 a 1 b 1 a 0 b 0 a 2 b 0 a 1 b 1 a 0 b 2 a 1 b 0 a 0 b 1 a 0 b 0 a 3 b 1 a 2 b 2 a 1 b 3 a 3 b 0 a 2 b 1 a 1 b 2 a 0 b 3 p 4 p 3 p 2 p 1 p 0 Jin-Fu Li, EE, NCU 25

Datapath – Multipliers The product axb is given by the 8 -bit result p=p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 The ith product term pi can be expressed as pi a b i j k ci 1 Alternate view of multiplication process (a 3 p 7 p 6 a 2 p 5 Advanced Reliable Systems (ARES) Lab. (a 3 a 2 a 1 p 4 a 3 a 2 a 1 a 0 b 3 b 2 b 1 b 0 (a 3 a 2 a 1 a 0) xb 0 a 1 a 0) xb 1 a 2 a 0) xb 2 a 1 a 0) xb 3 p 2 Jin-Fu Li, EE, NCU p 1 (axb 0)2 0 (axb 1)21 (axb 2)22 (axb 3)23 p 0 26

Datapath – Multipliers Using a product register for multiplication 7 6 5 4 3 2 1 0 Product register (axb 0)20 (axb 1)21 (axb 2)22 (axb 3)23 Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 27

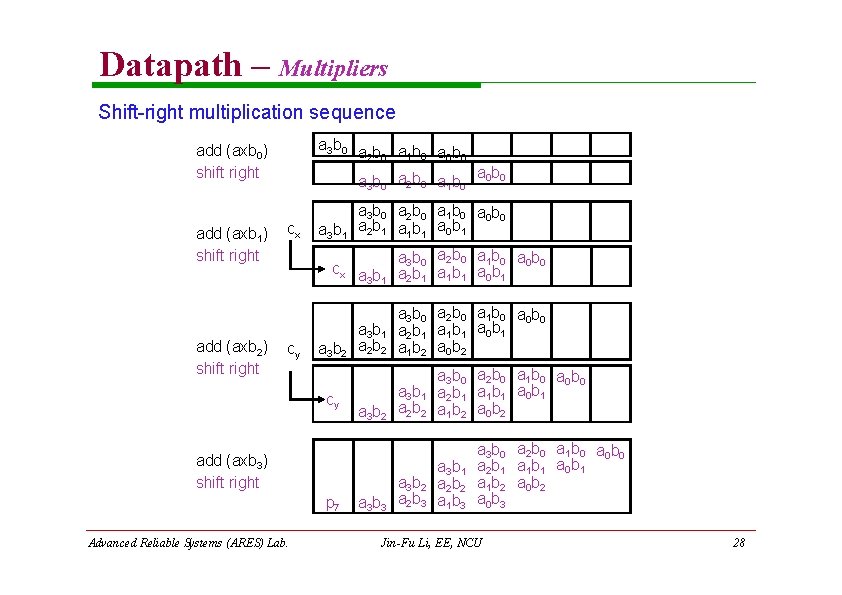
Datapath – Multipliers Shift-right multiplication sequence a 3 b 0 a b a b 1 0 2 0 0 0 add (axb 0) shift right add (axb 1) shift right add (axb 2) shift right ab a 3 b 0 a 2 b 0 a 1 b 0 0 0 cx cy a 3 b 1 a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 a 2 b 1 a 1 b 1 a 0 b 1 cx a b 3 1 a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 a 2 b 1 a 1 b 1 a 0 b 1 a 3 b 1 a 2 b 2 a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 a 2 b 1 a 1 b 1 a 0 b 1 a 1 b 2 a 0 b 2 a 3 b 2 cy a 3 b 2 add (axb 3) shift right p 7 Advanced Reliable Systems (ARES) Lab. a 3 b 3 a 3 b 1 a 2 b 2 a 3 b 2 a 2 b 3 a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 a 2 b 1 a 1 b 1 a 0 b 1 a 1 b 2 a 0 b 2 a 3 b 1 a 2 b 2 a 1 b 3 a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 a 2 b 1 a 1 b 1 a 0 b 1 a 1 b 2 a 0 b 3 Jin-Fu Li, EE, NCU 28

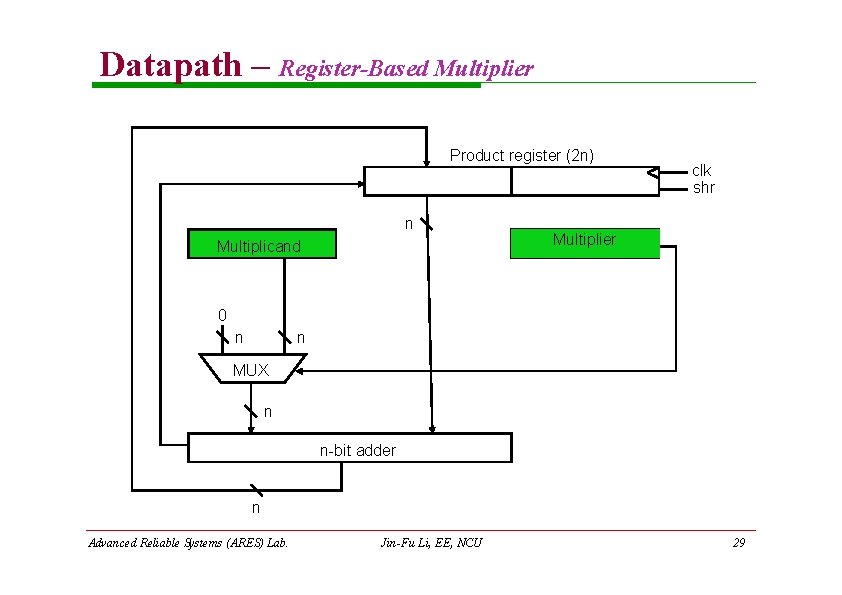
Datapath – Register-Based Multiplier Product register (2 n) n Multiplicand clk shr Multiplier 0 n n MUX n n-bit adder n Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 29

Datapath – Array Multipliers Consider two unsigned binary integers X and Y n 1 Y Yj 2 j X Xi 2 i j 0 i 0 n 1 j 0 P X Y X i 2 i Y j 2 j n 1 (X i 0 j 0 i Y j )2 i j n n 1 Pk 2 k k 0 Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 30

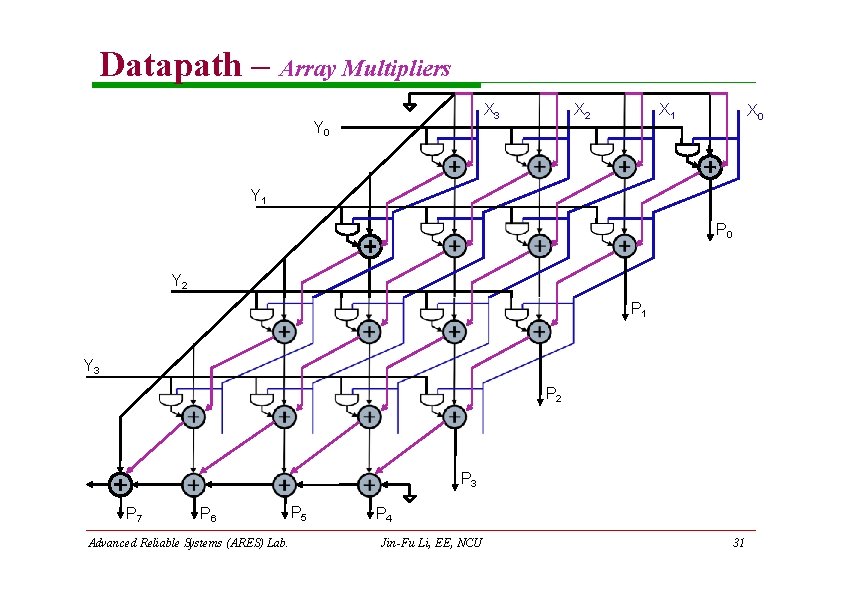
Datapath – Array Multipliers X 3 Y 0 X 2 X 1 X 0 Y 1 P 0 Y 2 P 1 Y 3 P 2 P 3 P 7 P 6 Advanced Reliable Systems (ARES) Lab. P 5 P 4 Jin-Fu Li, EE, NCU 31

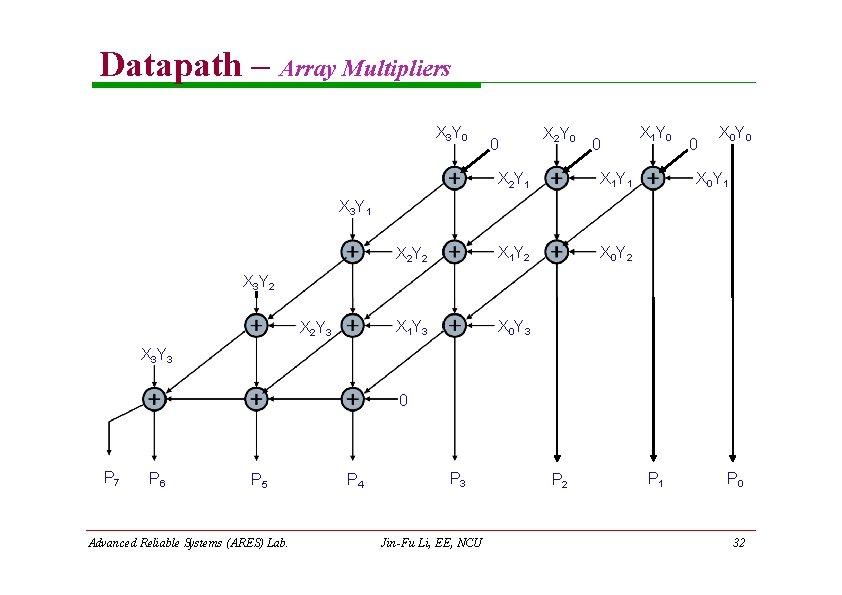
Datapath – Array Multipliers X 3 Y 0 0 X 2 Y 1 X 1 Y 1 X 2 Y 2 X 1 Y 2 X 0 Y 2 X 1 Y 3 X 0 Y 3 X 1 Y 0 0 X 0 Y 1 X 3 Y 2 X 2 Y 3 X 3 Y 3 0 P 7 P 6 P 5 Advanced Reliable Systems (ARES) Lab. P 4 P 3 Jin-Fu Li, EE, NCU P 2 P 1 P 0 32

Datapath – Booth Multiplier Booth’s algorithm takes advantages of the fact that an adder-substractor is nearly as fast and small as a simple adder Consider the two’s complement representation of the multiplier y n 2 n y 2 n 1 y y 2 2 yn 2 � n 1 n The representation can be rewritten as n 1 n 2 n ) 2 (y y ) 2 (yn 3 yn 2 ) � y 2 (yn 1 yn n 2 n 1 Extract the first two terms n y ) 2 n 1 (y y ) y 2 (y n 1 n n 2 n 1 The right-hand term can be used to add x to partial product The left-hand term add 2 x Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 33

Datapath – Booth Multiplier Actions during Booth multiplication y i 1 y i 2 Operation 0 0 0 1 Add x 0 1 0 Add x 0 1 1 Add 2 x 1 1 0 0 0 1 Sub 2 x 1 1 0 1 1 1 Add 0 Sub x Add 0 For example, x=011001 (2510), y=101110 (-1810) 1. 2. y 1 y 0 y-1=100, so P 1=P 0 -2 x. 1=11111001110 y 3 y 2 y 1=111, so P 2=P 1+0. 4=11111001110 3. y 5 y 4 y 3=101, so P 3=P 2 -x. 16=11000111110 Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 34

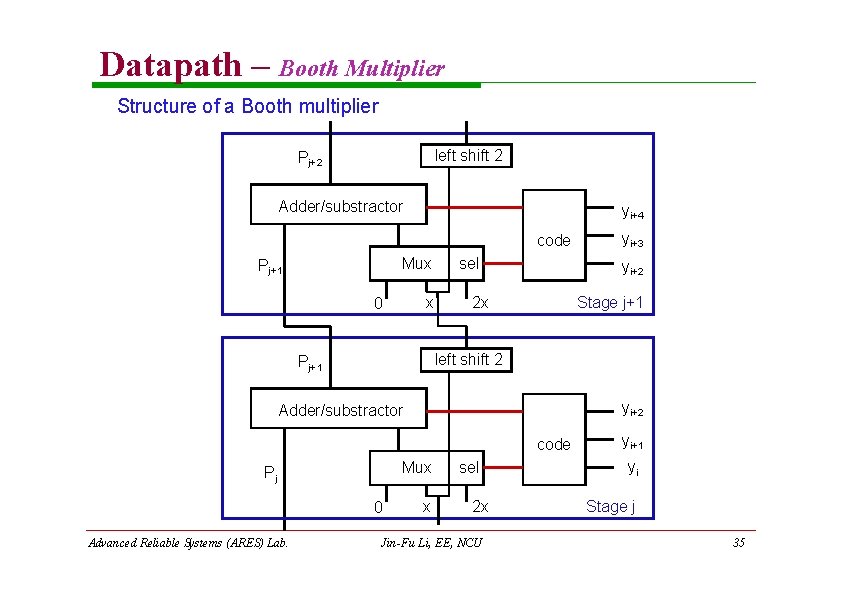
Datapath – Booth Multiplier Structure of a Booth multiplier left shift 2 Pj+2 Adder/substractor yi+4 code Mux Pj+1 x 0 sel yi+2 2 x Stage j+1 left shift 2 Pj+1 yi+2 Adder/substractor code Mux Pj 0 Advanced Reliable Systems (ARES) Lab. yi+3 x sel 2 x Jin-Fu Li, EE, NCU yi+1 yi Stage j 35

Datapath – Wallace Tree Multiplier A Wallace tree is a full adder tree structured specially for a quick addition of the partial products Example A 16 x 16 Booth multiplier 8 partial products are generated Assume that all partial products are negative so all sign extension bits are 1’s Sign extension correction vector is 1010101011 11111111111111 11111 111111 11 1010101011 Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 36

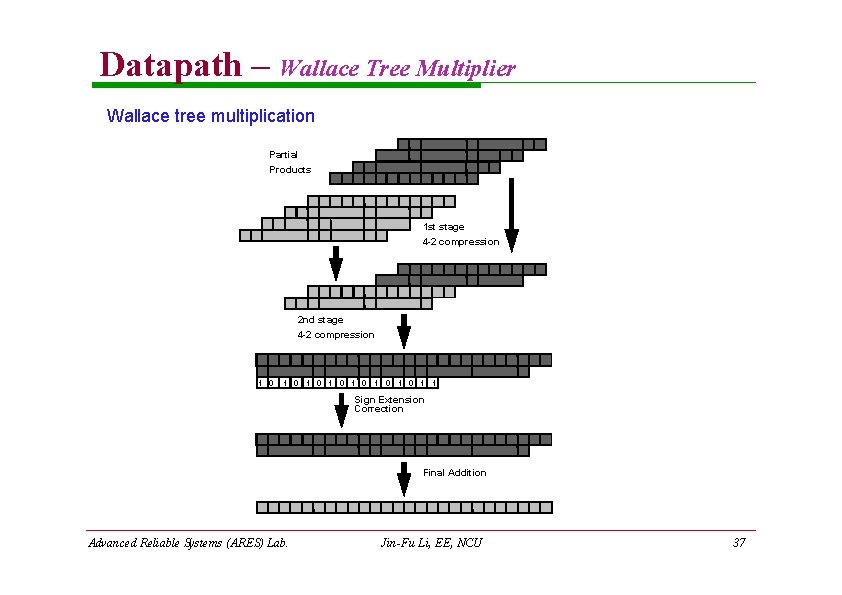
Datapath – Wallace Tree Multiplier Wallace tree multiplication Partial Products 1 st stage 4 -2 compression 2 nd stage 4 -2 compression 1 0 1 0 1 1 Sign Extension Correction Final Addition Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 37

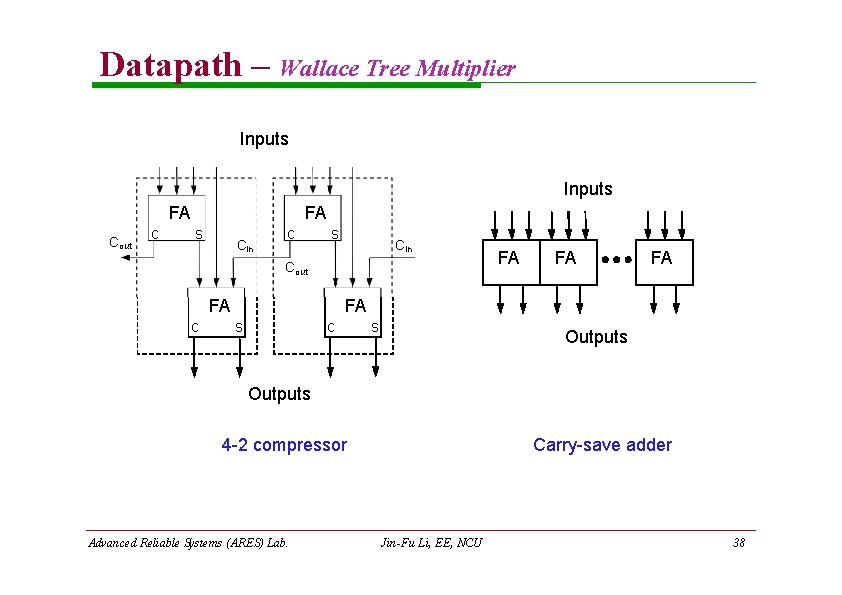
Datapath – Wallace Tree Multiplier Inputs FA Cout c FA s Cin c s Cin Cout FA c FA FA s c s Outputs 4 -2 compressor Advanced Reliable Systems (ARES) Lab. Carry-save adder Jin-Fu Li, EE, NCU 38

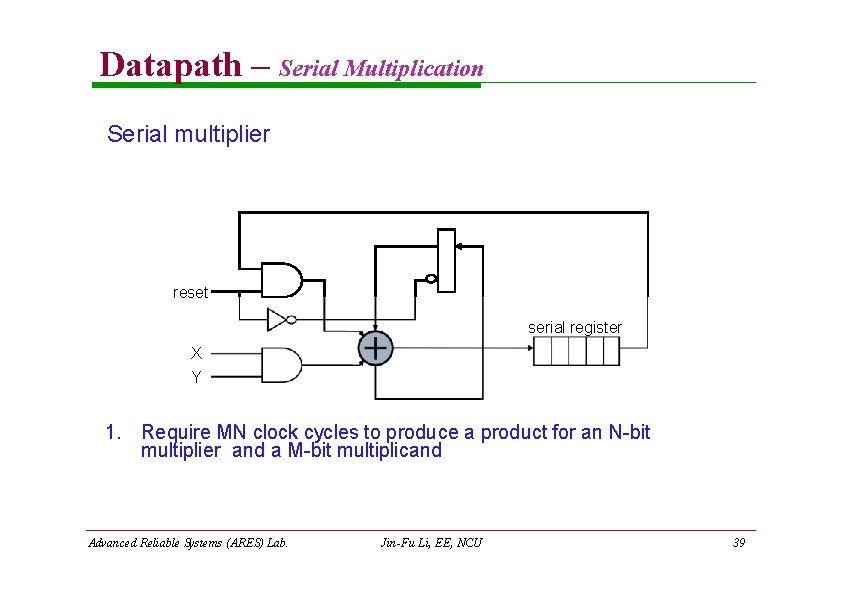
Datapath – Serial Multiplication Serial multiplier reset serial register X Y 1. Require MN clock cycles to produce a product for an N-bit multiplier and a M-bit multiplicand Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 39

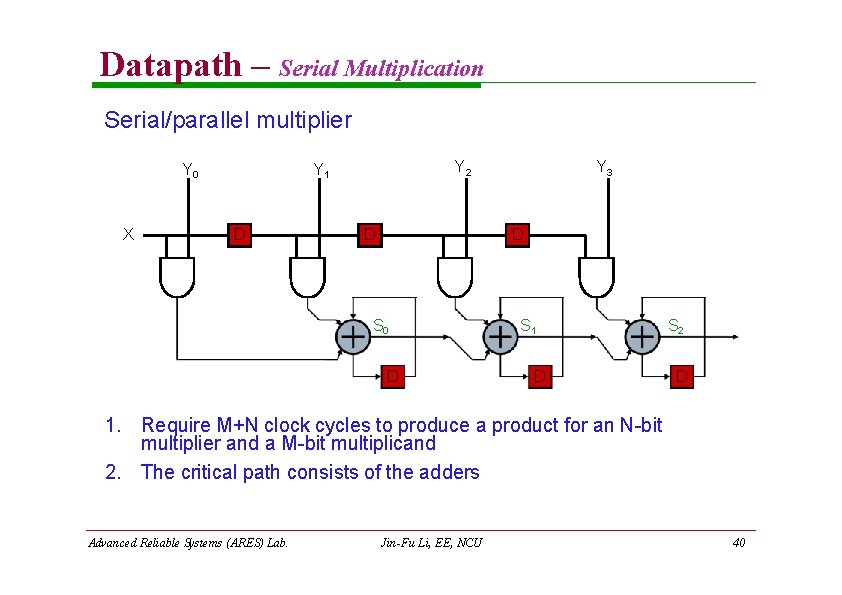
Datapath – Serial Multiplication Serial/parallel multiplier Y 0 X Y 2 Y 1 D D Y 3 D S 0 D S 1 D S 2 D 1. Require M+N clock cycles to produce a product for an N-bit multiplier and a M-bit multiplicand 2. The critical path consists of the adders Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 40

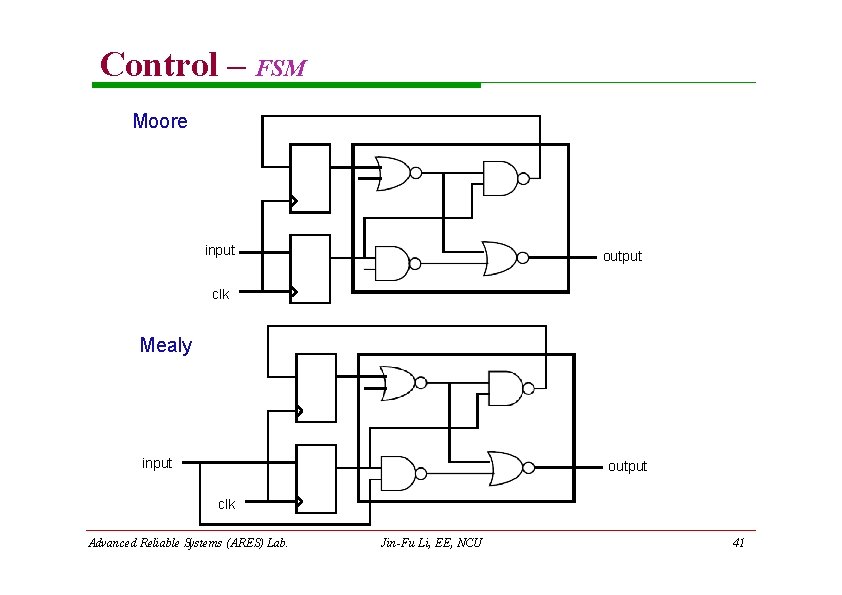
Control – FSM Moore input output clk Mealy input output clk Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 41

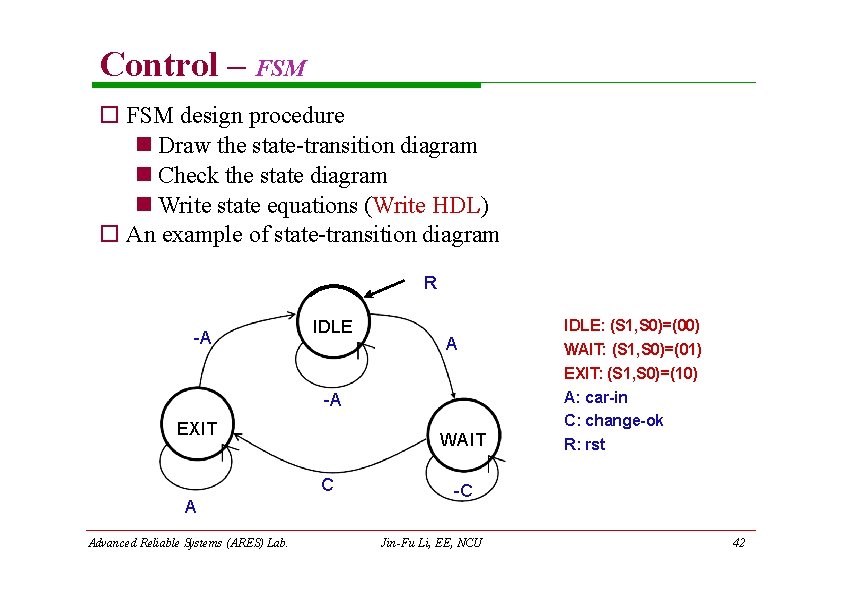
Control – FSM design procedure Draw the state-transition diagram Check the state diagram Write state equations (Write HDL) An example of state-transition diagram R -A IDLE A -A EXIT WAIT C A Advanced Reliable Systems (ARES) Lab. IDLE: (S 1, S 0)=(00) WAIT: (S 1, S 0)=(01) EXIT: (S 1, S 0)=(10) A: car-in C: change-ok R: rst -C Jin-Fu Li, EE, NCU 42

Control – FSM Check the state-transition diagram Ensure all states are represented, including the IDLE state Check that the OR of all transitions leaving a state is TRUE. This is a simple method of determining that there is a way out of a state once entered. Verify that the pairwise XOR of all exit transitions is TRUE. This ensures that there are not conflicting conditions that would lead to more than one exittransition becoming active at any time. Insert loops into any state if it is not guaranteed to otherwise change on each cycle. Formal FSM verification method Perform conformance checking Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 43

Control – Verilog Coding Style for FSMs module toll_booth(clk, rst, car_in, change_ok, green); clk, rst, car_in, change_ok; input output green; reg[1: 0] state_reg, next_state; parameter IDLE = 2’b 00; parameter WAIT = 2’b 01; parameter EXIT = 2’b 11; always @(posedge clk or posedge rst) begin If (rst==1’b 1) state_reg<=IDLE; else state_reg<=next_state; end always @(state_reg or car_in or change_ok) begin case(state_reg): IDLE: if (car_in==1’ 1) begin next_state=WAIT; green=1’b 0; end else begin next_state=IDEL; end WAIT: if (change==1’b 1) begin next_state=EXIT; green=1’b 1; end else begin next_state=WAIT; green=1’b 0; end Advanced Reliable Systems (ARES) Lab. EXIT: if (car_in==1’ 1) begin next_state=EXIT; green=1’b 1; end else begin next_state=IDEL; green=1’b 0; end default: begin next_state=IDLE; green=1’b 0; endcase endmodule Jin-Fu Li, EE, NCU 44

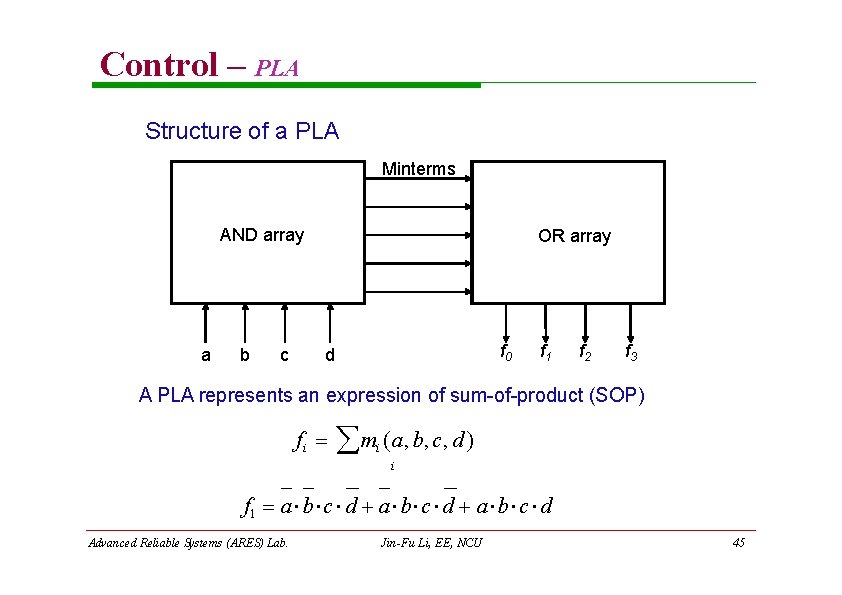
Control – PLA Structure of a PLA Minterms AND array a b c OR array f 0 d f 1 f 2 f 3 A PLA represents an expression of sum-of-product (SOP) f i mi (a, b, c, d ) i f 1 a b c d Advanced Reliable Systems (ARES) Lab. Jin-Fu Li, EE, NCU 45

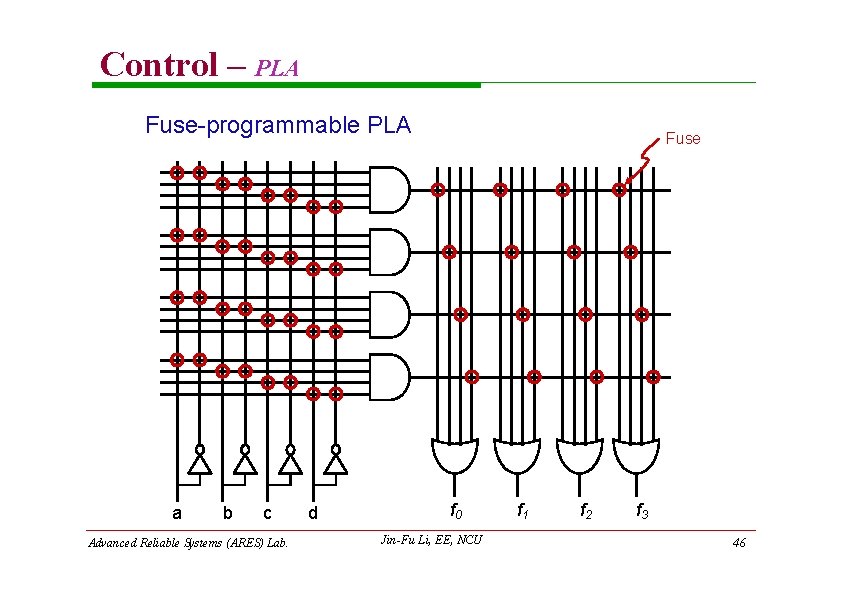
Control – PLA Fuse-programmable PLA a b c Advanced Reliable Systems (ARES) Lab. d Fuse f 0 Jin-Fu Li, EE, NCU f 1 f 2 f 3 46

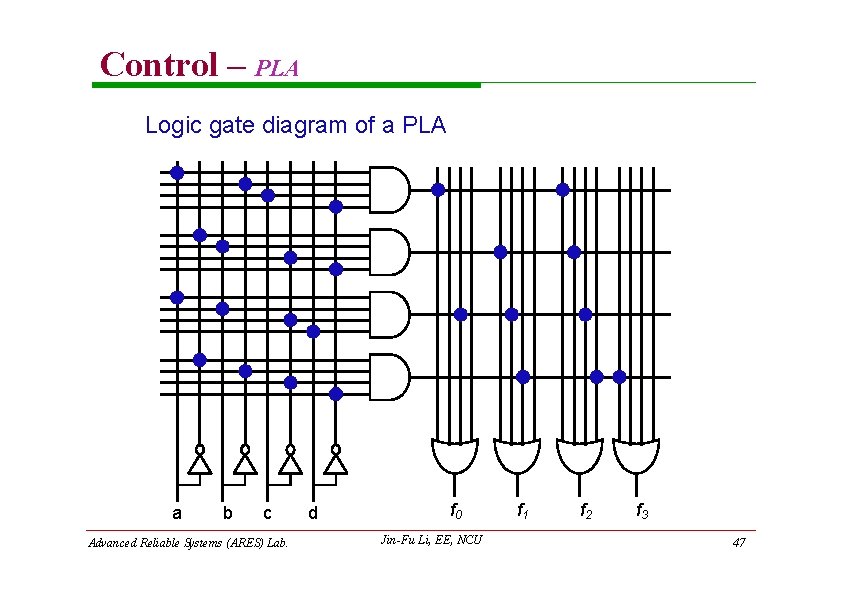
Control – PLA Logic gate diagram of a PLA a b c Advanced Reliable Systems (ARES) Lab. d f 0 Jin-Fu Li, EE, NCU f 1 f 2 f 3 47