Chapter 3 Vector 1 Adding Vectors Geometrically 2






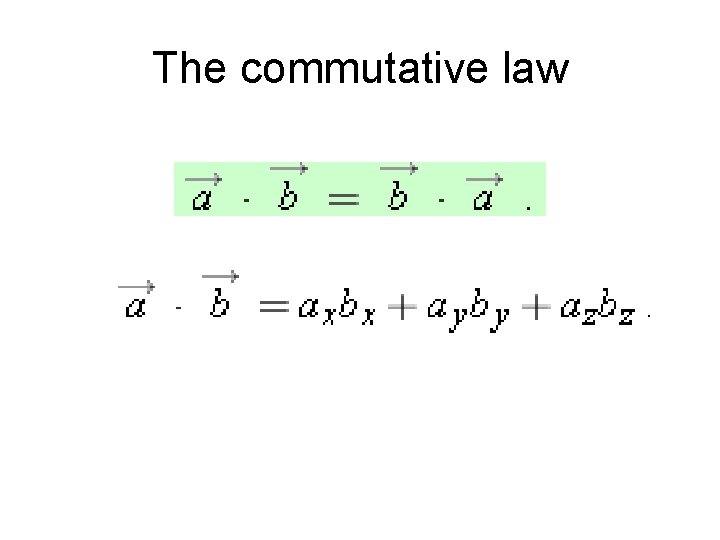
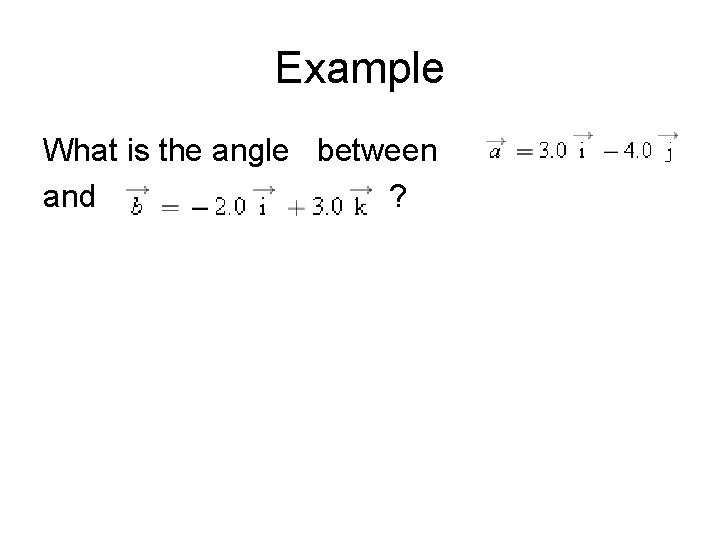


- Slides: 22

Chapter 3. Vector 1. Adding Vectors Geometrically 2. Components of Vectors 3. Unit Vectors 4. Adding Vectors by Components 5. Multiplying Vectors

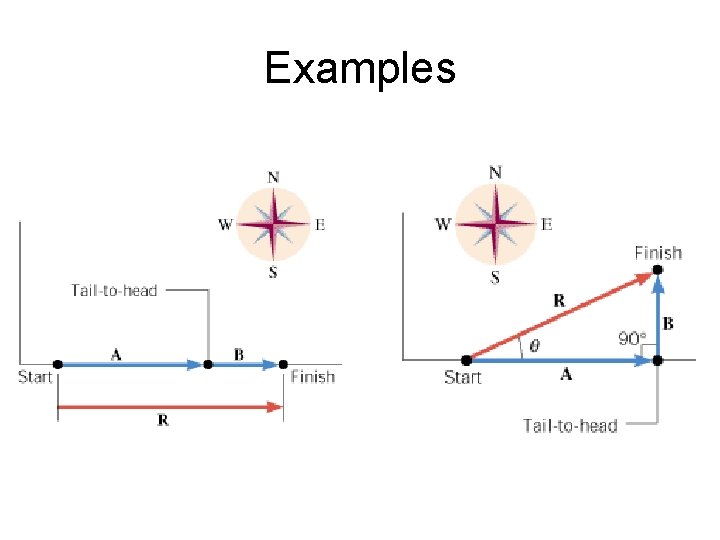
Adding Vectors Graphically General procedure for adding two vectors graphically: • (1) On paper, sketch vector to some convenient scale and at the proper angle. • (2) Sketch vector to the same scale, with its tail at the head of vector , again at the proper angle. • (3) The vector sum is the vector that extends from the tail of to the head of .

Examples

Two important properties of vector additions (1) Commutative law: (2) Associative law:

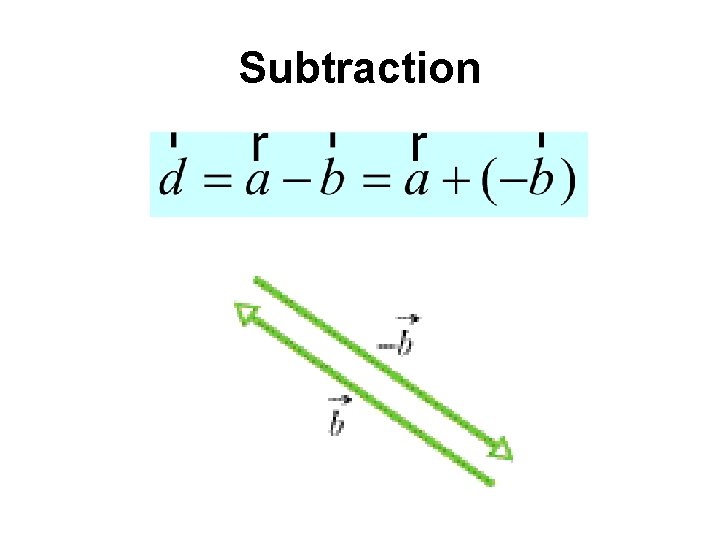
Subtraction

Check Your Understanding Two vectors, A and B, are added by means of vector addition to give a resultant vector R: R=A+B. The magnitudes of A and B are 3 and 8 m, but they can have any orientation. What is (a) the maximum possible value for the magnitude of R? (b) the minimum possible value for the magnitude of R?

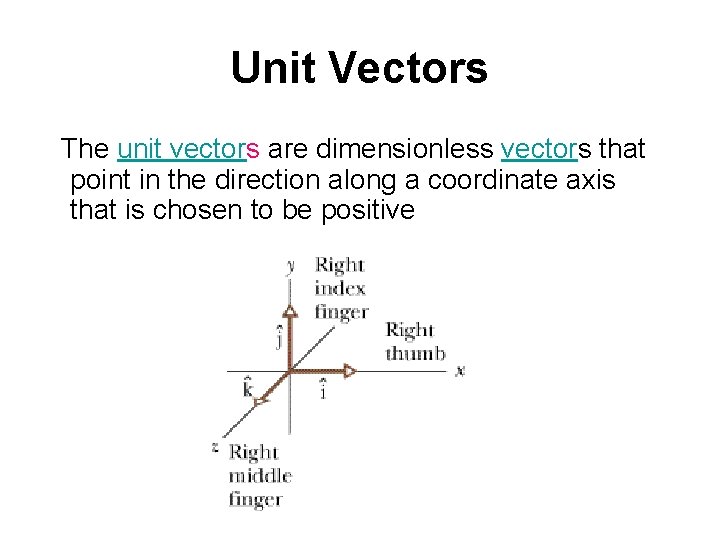
Unit Vectors The unit vectors are dimensionless vectors that point in the direction along a coordinate axis that is chosen to be positive

How to describe a two-dimension vector? Vector Components: The projection of a vector on an axis is called its component.

Properties of vector component • The vector components of the vector depend on the orientation of the axes used as a reference. • A scalar is a mathematical quantity whose value does not depend on the orientation of a coordinate system. The magnitude of a vector is a true scalar since it does not change when the coordinate axis is rotated. However, the components of vector (Ax, Ay) and (Ax′, Ay′), are not scalars. • It is possible for one of the components of a vector to be zero. This does not mean that the vector itself is zero, however. For a vector to be zero, every vector component must individually be zero. • Two vectors are equal if, and only if, they have the same magnitude and direction

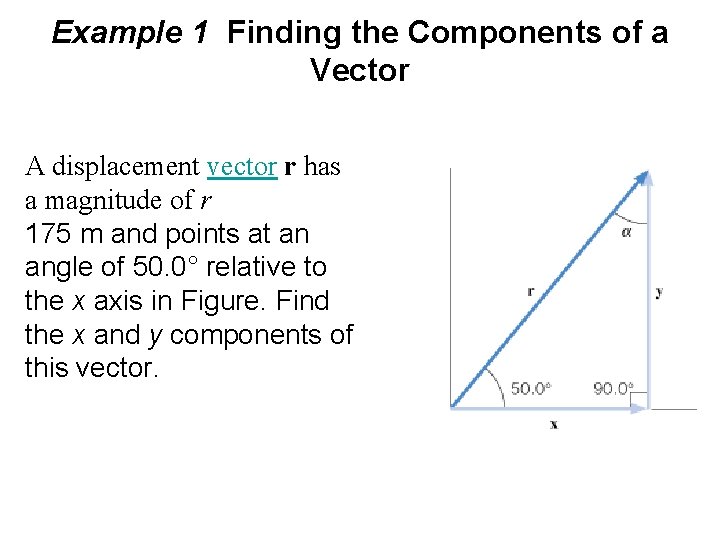
Example 1 Finding the Components of a Vector A displacement vector r has a magnitude of r 175 m and points at an angle of 50. 0° relative to the x axis in Figure. Find the x and y components of this vector.

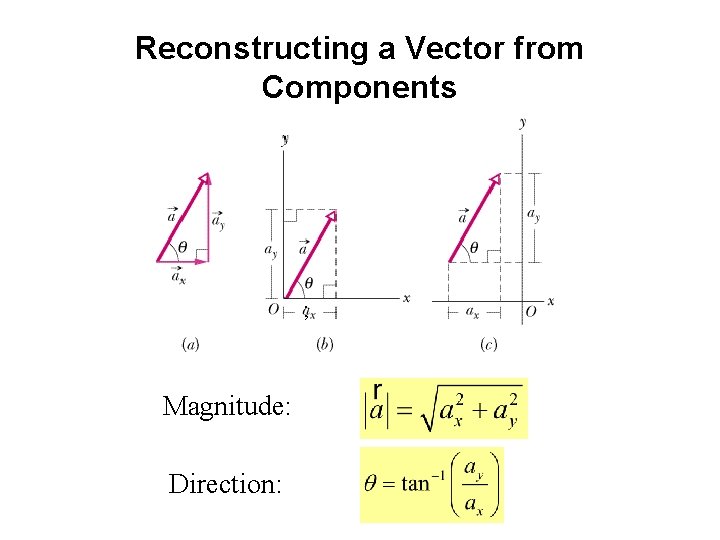
Reconstructing a Vector from Components ; Magnitude: Direction:

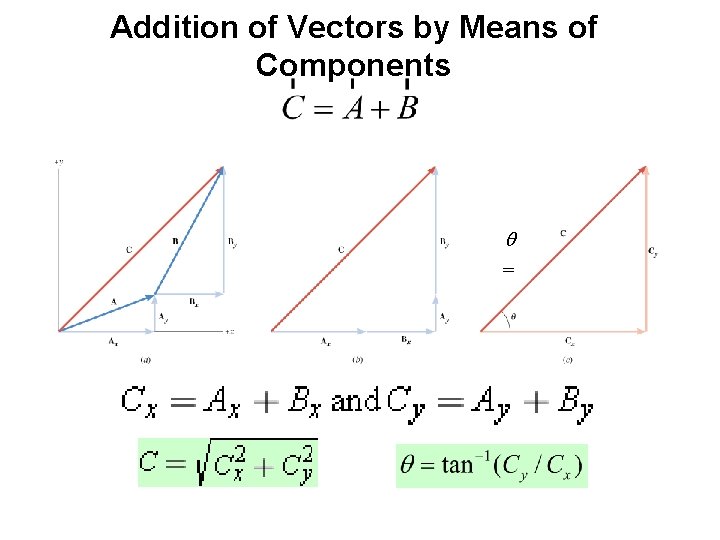
Addition of Vectors by Means of Components q =

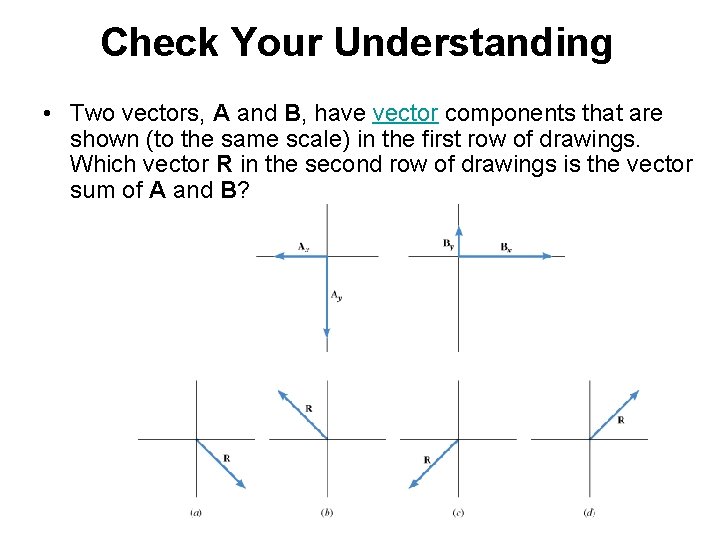
Check Your Understanding • Two vectors, A and B, have vector components that are shown (to the same scale) in the first row of drawings. Which vector R in the second row of drawings is the vector sum of A and B?

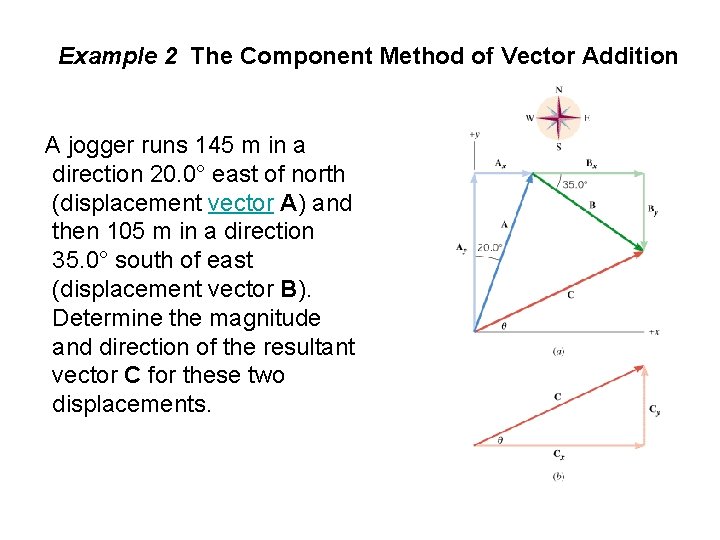
Example 2 The Component Method of Vector Addition A jogger runs 145 m in a direction 20. 0° east of north (displacement vector A) and then 105 m in a direction 35. 0° south of east (displacement vector B). Determine the magnitude and direction of the resultant vector C for these two displacements.

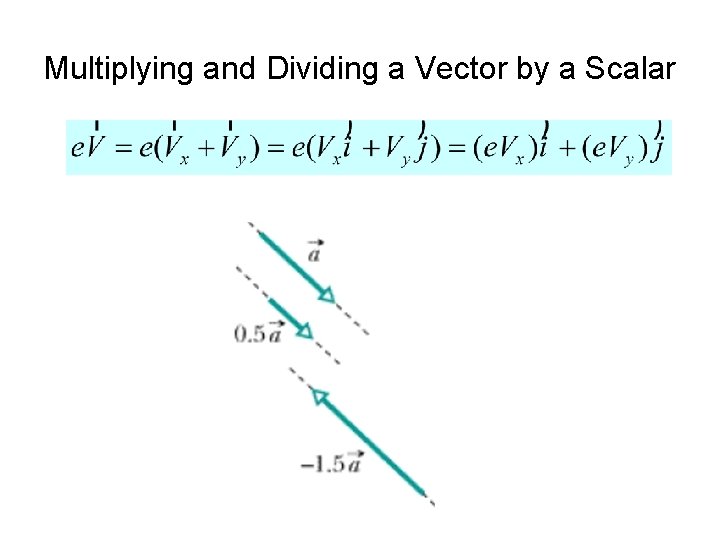
Multiplying and Dividing a Vector by a Scalar

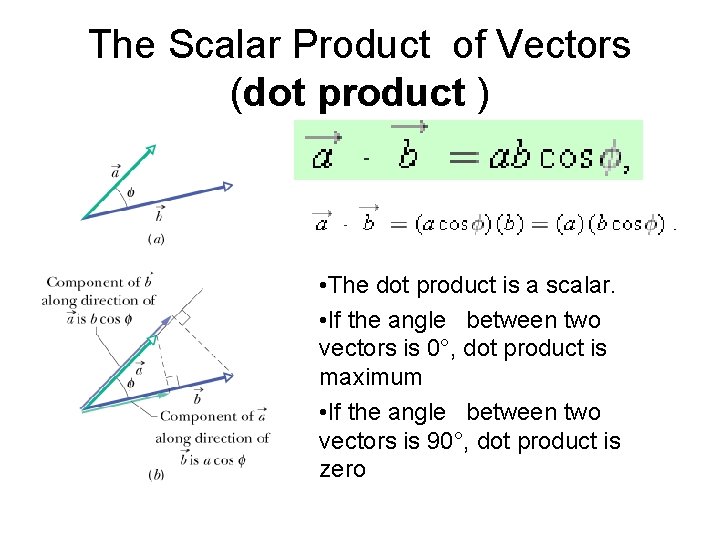
The Scalar Product of Vectors (dot product ) • The dot product is a scalar. • If the angle between two vectors is 0°, dot product is maximum • If the angle between two vectors is 90°, dot product is zero
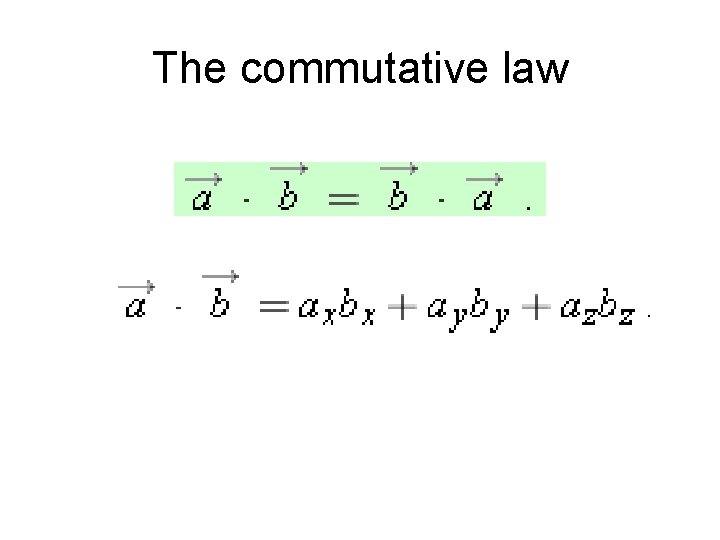
The commutative law
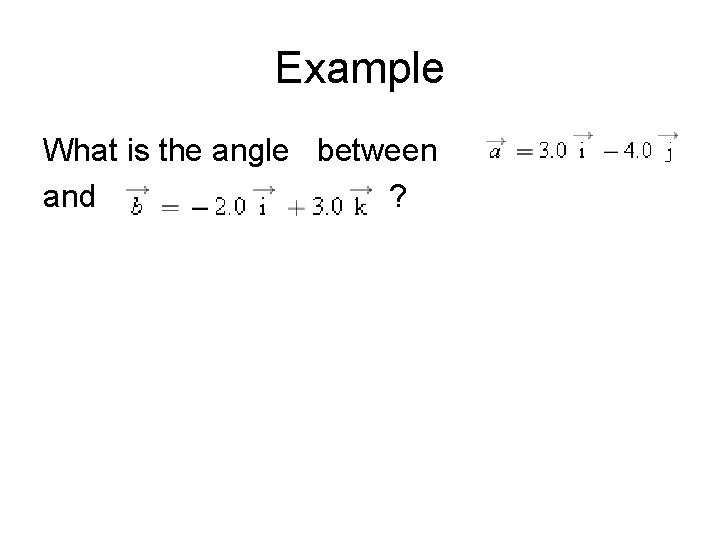
Example What is the angle between and ?

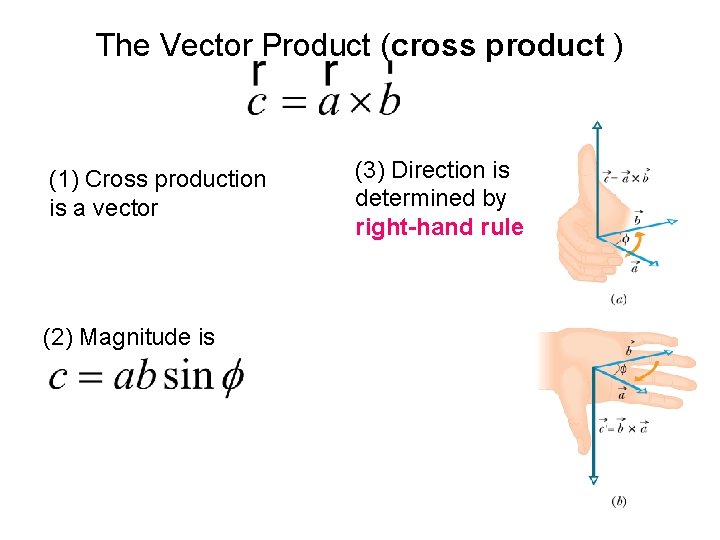
The Vector Product (cross product ) (1) Cross production is a vector (2) Magnitude is (3) Direction is determined by right-hand rule

Property of vector cross product • The order of the vector multiplication is important. If two vectors are parallel or anti-parallel, . If two vectors are perpendicular to each other , the magnitude of their cross product is maximum.

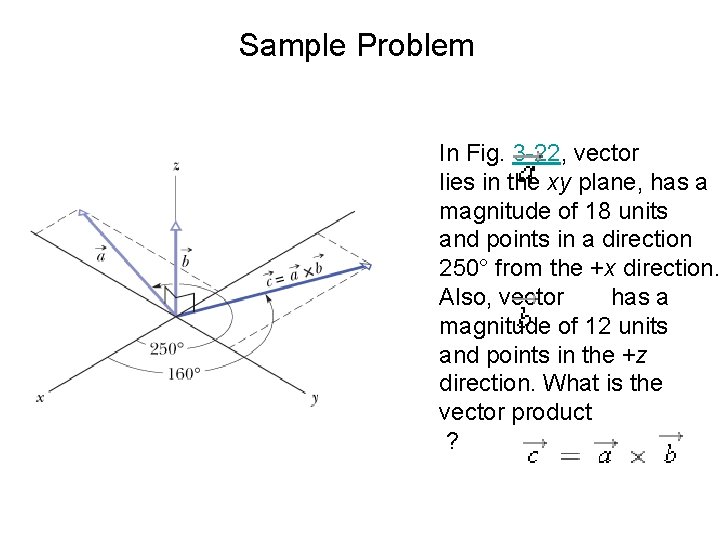
Sample Problem In Fig. 3 -22, vector lies in the xy plane, has a magnitude of 18 units and points in a direction 250° from the +x direction. Also, vector has a magnitude of 12 units and points in the +z direction. What is the vector product ?

Sample Problem If and , what is ?