chapter 3 Unit and Recipe Conversions Class Name

chapter 3 Unit and Recipe Conversions Class Name Instructor Name Date, Semester Foundations of Cost Control Daniel Traster

Opening Questions What is the difference between weight and volume? Are they interchangeable? Which tools measure weight and which measure volume? 2

Water Universal Water is interchangeable at 1 pt = 1 # or 1 c = 8 oz Because of this constant, you can convert between volume and weight on paper in intermediate steps as long as you return to the original type of measure (weight vs. volume) at the end. 3

Table 3. 1 • Review table 3. 1 • Which measures are American/British? • Which are metric? 4

Table 3. 2 and Figure 3. 1 • These facts must be memorized in order to convert units • Practice daily until they become second nature • You cannot convert units without them! 5

Three Methods to Convert Units Unit Size Operation Technique Left/Right Operation Technique • You only have to learn one • Choose the one that makes the most sense to you Dimensional Analysis 6

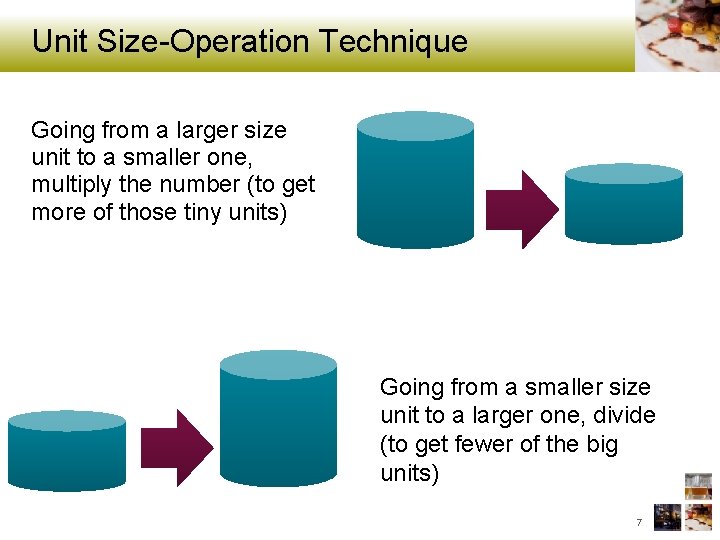
Unit Size-Operation Technique Going from a larger size unit to a smaller one, multiply the number (to get more of those tiny units) Going from a smaller size unit to a larger one, divide (to get fewer of the big units) 7

Example 3 a How many ounces are in 2 ¼ pounds? Pounds (big) to ounces (small) Unit down, number up = multiply Ratio is 16 oz = 1#, so multiply by 16 2. 25 # X 16 = 32 oz 8

Example 3 b 8 cups equals how many gallons? Cups (small) to gallons (big) Unit up, number down = divide Ratio is 16 c = 1 Gal 8 c ÷ 16 = ½ Gal 9

Example 3 c (requires intermediate steps) How many Kg of water are in 2 Gal? 1 Kg = 2. 2 #, 1 pt = 1#, 1 Gal = 8 pt 2 Gal (big) to pt (small) = multiply 2 Gal X 8 = 16 pt 1 pt = 1 #, so 16 pt = 16 # (small) to Kg (big) = divide 16 # ÷ 2. 2 = 7. 27 Kg 10

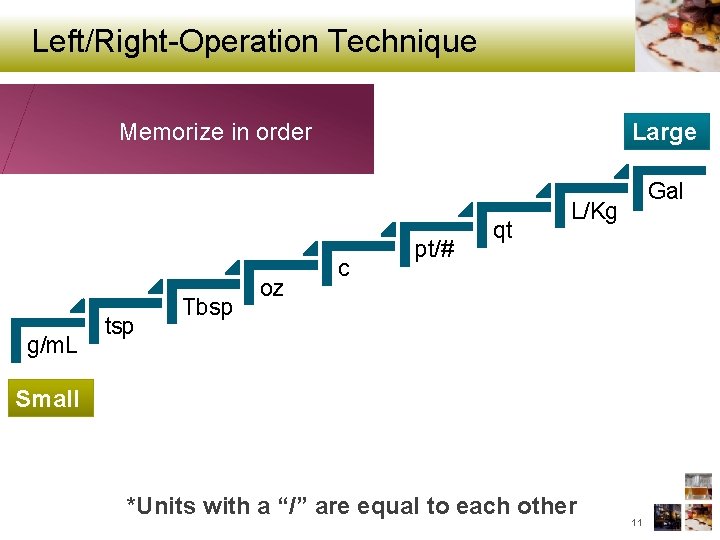
Left/Right-Operation Technique Large Memorize in order g/m. L tsp Tbsp oz c pt/# qt Gal L/Kg Small *Units with a “/” are equal to each other 11

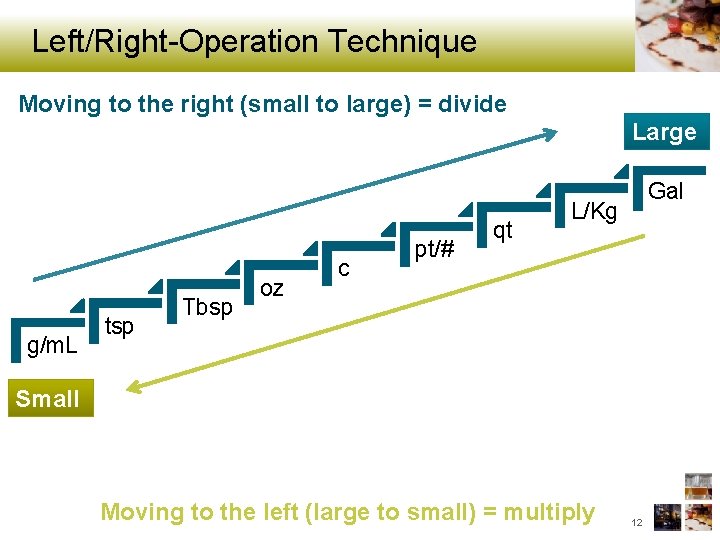
Left/Right-Operation Technique Moving to the right (small to large) = divide Large g/m. L tsp Tbsp oz c pt/# qt Gal L/Kg Small Moving to the left (large to small) = multiply 12

Example 3 d How many m. L are in ¾ L? Going from L to m. L, move left to right = multiply 1 L = 1000 m. L 0. 75 L X 1000 = 750 m. L 13

Example 3 e How many quarts are in 17 cups? Going cups to quarts you move left to right = divide 1 qt = 4 c 17 c ÷ 4 = 4. 25 or 4 ¼ qt 14

Example 3 f (requires intermediate step) How many m. L are in a 16 oz bottle of water? 1000 m. L = 1 L and 1 L = 33. 8 oz Move oz to L (left to right) = divide 16 oz ÷ 33. 8 = 0. 47337 L (don’t round on an intermediate step) Move L to m. L (right to left) = multiply 0. 47337 X 1000 = 473. 37 or 473. 4 m. L 15

Dimensional Analysis 1. Write the ratios as fractions 2. Orient the fractions to the units cancel (each denominator’s unit is the same as the preceding numerator’s unit) 3. Multiply the fractions 4. Any units not canceled out remain in the answer in their same position (numerator or denominator) 16

Example 3 g How many L does 2 ¾ pt represent? L = 33. 8 oz and 1 pt = 16 oz 2. 75 pt X X = 1. 302 L or 1. 3 L To compute, enter the starting number in a calculator. Then multiply by the numerators and divide by the denominators. 17

Example 3 h How many cups are there in 2. 35 gallons? 1 Gal = 16 c 2. 35 Gal X = 37. 6 c 18

Why are Recipes Converted? • Chef may have a recipe using metric (or British) units but the kitchen tools only measure in the other system’s units • Chef has converted a recipe’s yield, and it is more practical to measure the ingredients in different units 19

How to Adjust a Recipe’s Yield STEP 1: You must know the original (old) yield and the desired (new) yield for the recipe. Calculate a conversion factor (CF) CF = 20

Example 3 i What is the conversion factor to change a recipe yielding 75 portions to one yielding 20 portions? CF = = = 0. 266 or 0. 27 21

Conversion Factor If the portion size of the recipe changes, you must calculate the total weight (or volume) of each recipe’s yield before using the conversion factor formula. Total Yield = total portions X portion size 22

Example 3 j Calculate CF to convert a recipe yielding 4 onepound loaves of bread to one yielding 110 twoounce rolls. Old Yield = portions X size = 4 X 1 # = 4 # New = 110 X 2 oz = 220 oz The units don’t match!!! Convert # to oz before proceeding 4 # X 16 = 64 oz 23

Example 3 j (cont. ) CF = = = 3. 4375 or 3. 44 The formula only works if the units for new and old yield match. 24

How to Adjust a Recipe’s Yield STEP 2: Multiply the conversion factor times each ingredient in the recipe to get a recipe that will produce the new yield. New Ingredient Quantity = Old Ing. Q X CF The biggest challenge is converting the unit to make the new ingredient quantity measurements practical in the real world. 25

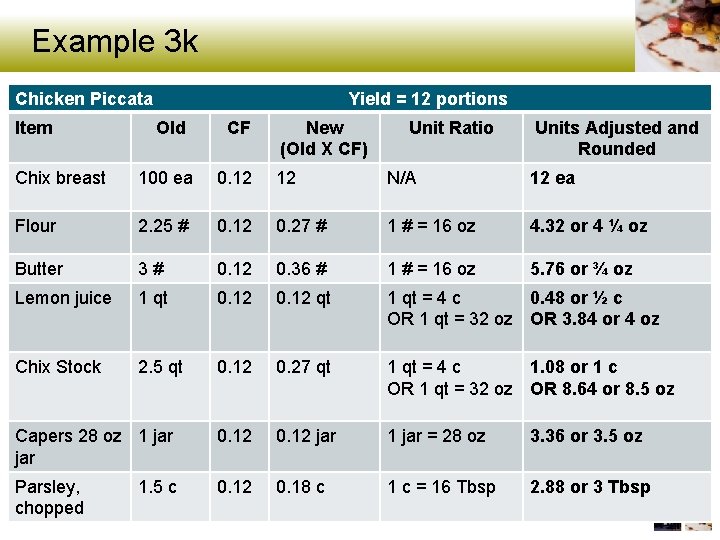
Example 3 k Convert the following recipe to serve 12 portions. Chicken Piccata Yield = 100 portions Chicken breast, boneless, 4 oz, pounded flat 100 ea Flour, all-purpose 2 ¼ # Butter 3 # Lemon juice 1 qt Chicken stock 2 ½ qt Capers, drained, 28 oz jar 1 jar Parsley, chopped fine 1 ½ c 26

Example 3 k (cont. ) CF = = = 0. 12 Multiply 0. 12 X each ingredient’s quantity 27

Example 3 k Chicken Piccata Yield = 12 portions Item Old CF Chix breast 100 ea 0. 12 12 N/A 12 ea Flour 2. 25 # 0. 12 0. 27 # 1 # = 16 oz 4. 32 or 4 ¼ oz Butter 3 # 0. 12 0. 36 # 1 # = 16 oz 5. 76 or ¾ oz Lemon juice 1 qt 0. 12 qt 1 qt = 4 c 0. 48 or ½ c OR 1 qt = 32 oz OR 3. 84 or 4 oz Chix Stock 2. 5 qt 0. 12 0. 27 qt 1 qt = 4 c 1. 08 or 1 c OR 1 qt = 32 oz OR 8. 64 or 8. 5 oz Capers 28 oz 1 jar 0. 12 jar 1 jar = 28 oz 3. 36 or 3. 5 oz Parsley, chopped 0. 12 0. 18 c 1 c = 16 Tbsp 2. 88 or 3 Tbsp 1. 5 c New (Old X CF) Unit Ratio Units Adjusted and Rounded

Notes on 3 k Solution • No unit conversion for “each. ” • Rounding depends on measurement tools available. • Lemon juice and stock convert to oz only because they are mostly water. • Non-standard ratios (1 jar = 28 oz) are learned from labels or a kitchen test. • Choice of unit and how much to round can impact precision of the measurement. 29