Chapter 3 Two Dimensional Motion and Vectors Now

Chapter 3: Two Dimensional Motion and Vectors (Now the fun really starts)

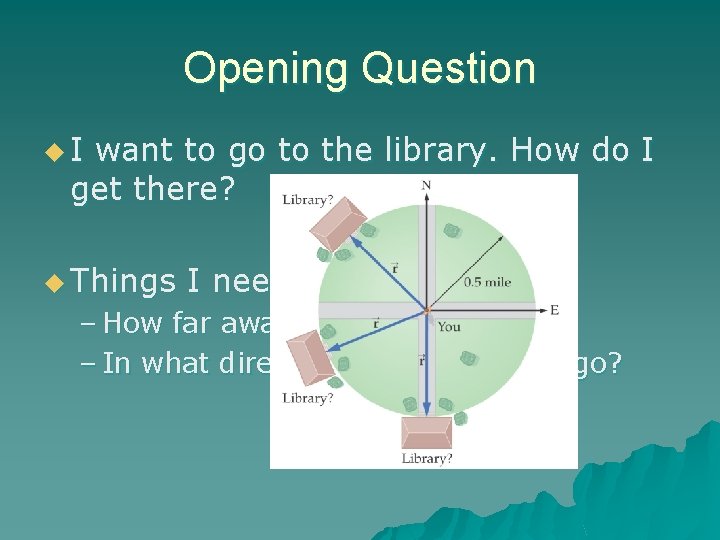
Opening Question u. I want to go to the library. How do I get there? u Things I need to know: – How far away is it? – In what direction(s) do I need to go?

One dimensional motion vs two dimensional motion u One dimensional motion: Limited to moving in one dimension (i. e. back and forth or up and down) u Two dimensional motion: Able to move in two dimensions (i. e. forward then left then back)

Scalars and Vectors u Scalar: A physical quantity that has magnitude but no direction – Examples: – Speed, Distance, Weight, Volume u Vector: A physical quantity that has both magnitude and direction – Examples: – Velocity, Displacement, Acceleration

Vectors are represented by symbols u Book uses boldface type to indicate vectors u Scalars u Use are designated with italics arrows to draw vectors

Vectors can be added graphically u When adding vectors make sure that the units are the same u Resultant vector: A vector representing the sum of two or more vectors

Adding Vectors Graphically u Draw situation using a reasonable scale (i. e. 50 m = 1 cm) u Draw each vector head to tail using the right scale u Use a ruler and protractor to find the resultant vector

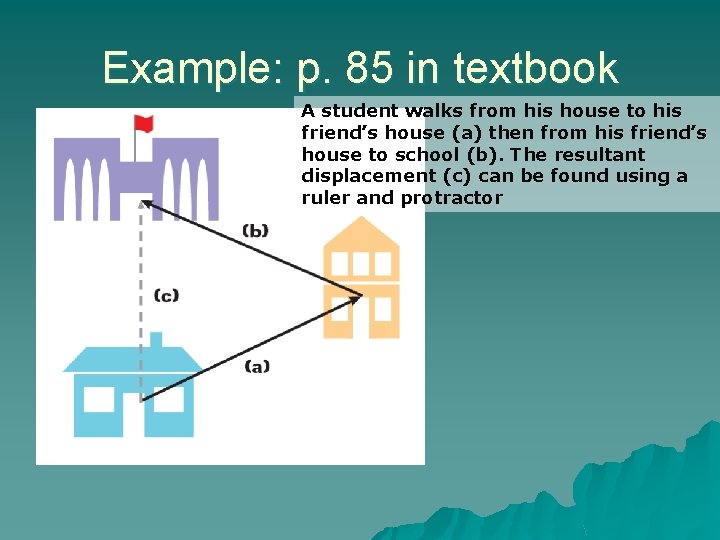
Example: p. 85 in textbook A student walks from his house to his friend’s house (a) then from his friend’s house to school (b). The resultant displacement (c) can be found using a ruler and protractor

Properties of vectors u Vectors u To can be added in any order subtract a vector add its opposite

Coordinate Systems u u u To perform vector operations algebraically we must use trigonometry SOH CAH TOA Pythagorean Theorem:

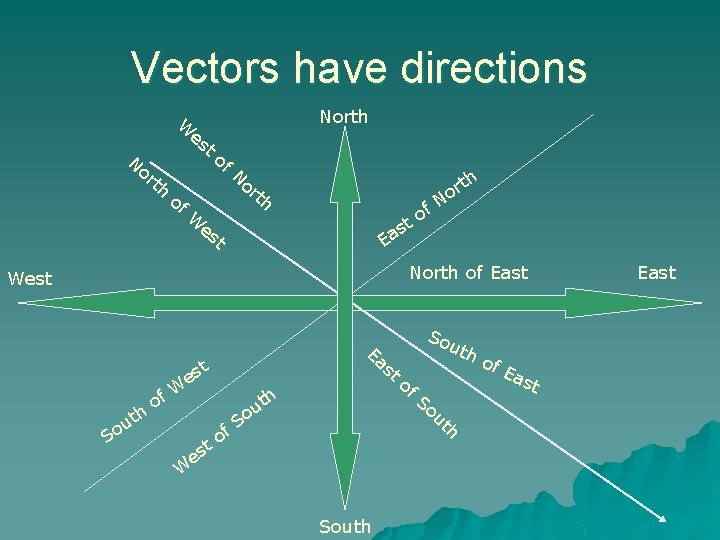
Vectors have directions North W es N t or th of of N th or or N f o t W th es s a E t North of East West Ea s t es h t u o t f. W to S W h t u o o es So uth of So ut f. S South h of Ea st East

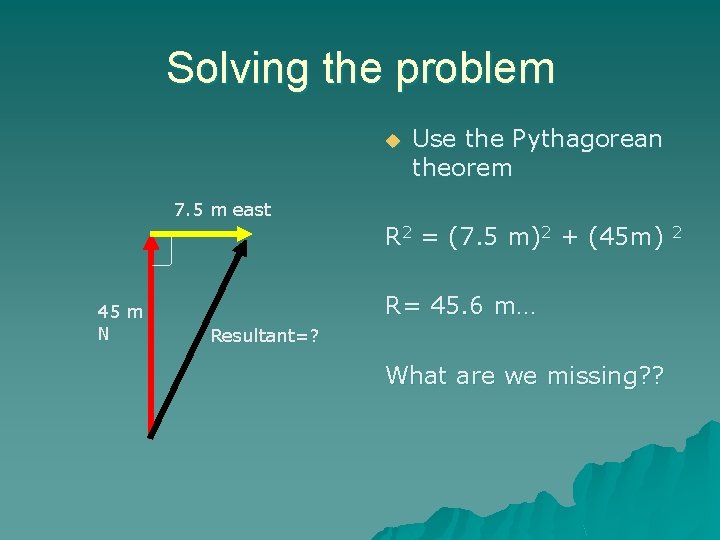
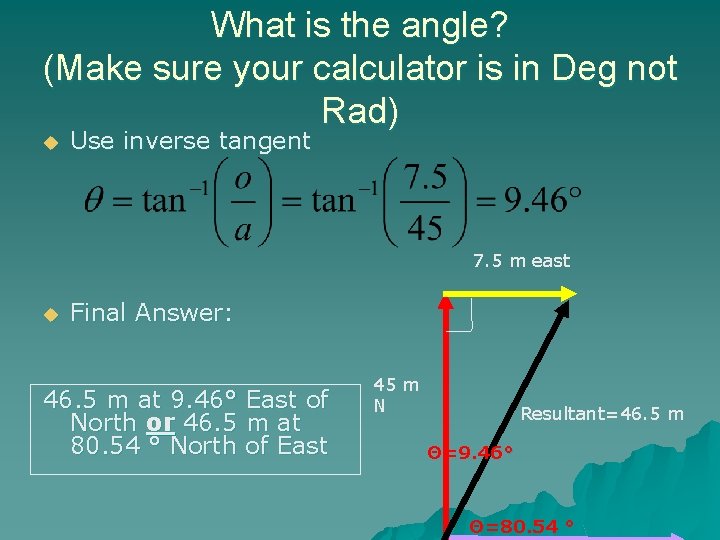
Examples p. 91 #2 u While following directions on a treasure map, a pirate walks 45. 0 m north then turns around and walks 7. 5 m east. What single straight-line displacement could the pirate have taken to reach the treasure?

Solving the problem u Use the Pythagorean theorem 7. 5 m east R 2 = (7. 5 m)2 + (45 m) 45 m N R= 45. 6 m… Resultant=? What are we missing? ? 2

Find the direction 7. 5 m east u 45 m N Resultant=? u Can’t say it’s just NE because we don’t know the value of the angle Find the angle using trig

What is the angle? (Make sure your calculator is in Deg not Rad) u Use inverse tangent 7. 5 m east u Final Answer: 46. 5 m at 9. 46° East of North or 46. 5 m at 80. 54 ° North of East 45 m N Resultant=46. 5 m Θ=9. 46° Θ=80. 54 °