Chapter 3 TopDown Design with Functions and Classes

Chapter 3: Top-Down Design with Functions and Classes Problem Solving, Abstraction, and Design using C++ 6 e by Frank L. Friedman and Elliot B. Koffman Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

3. 1 Building Programs with Existing Information • Analysis and design phases provide much information to help plan and complete a program • Can start with data requirements to develop constant and variable declarations • Use the algorithm as a first step in coding executable statements Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 2

Case Study: Finding the Area and Circumference of a Circle • Problem statement Get the radius of a circle. Compute and display the circle’s area and circumference. • Analysis – input is the circle’s radius – need calculation for the area – need calculation for the circumference Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 3

Case Study: Data Requirements • Problem Constant PI = 3. 14159 • Problem input float radius // radius of a circle • Problem output float area // area of a circle float circum // circumference of a circle Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 4

Case Study: Formulas • Area of a circle = radius 2 • Circumference of a circle = 2 radius Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 5

Case Study: Design - Algorithm 1. 2. 3. 4. Get the circle radius Compute the area of circle Compute the circumference of circle Display area and circumference Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 6

Case Study: Design - Algorithm 1. Get the circle radius 2. Compute the area of circle 2. 1 Assign PI * radius to area 3. Compute the circumference of circle 3. 1 Assign 2 * PI * radius to circum 4. Display area and circumference Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 7

Listing 3. 2 Outline of area and circumference program Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 8

Listing 3. 3 Finding the area and circumference of a circle Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 9

Listing 3. 3 Finding the area and circumference of a circle (continued) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 10

Case Study: Testing • Radius of 5. 0 • Should get area of 78. 539… • Should get circumference of 31. 415. . . Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 11

Case Study: Weight of Flat Washers • Problem statement You work for a hardware company that manufactures flat washers. To estimate shipping costs, you company needs a program that computes the weight of a specified quantity of flat washers. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 12

Case Study: Weight of Flat Washers • Analysis – flat washer is like a small donut – need to know rim area, thickness, density – rim area will be computed from knowing the washer’s outer and inner diameters. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13

Case Study: Data Requirements • Problem Constant PI = 3. 14159 • Problem inputs float hole. Diameter float edge. Diameter float thickness float density float quantity // diameter of hole // diameter of outer edge // thickness of washer // density of material used // number of washers made Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 14

Case Study: Data Requirements • Problem output float weight // weight of batch of washers • Program Variables float hole. Radius float edge. Radius float rim. Area float unit. Weight // radius of hole // radius of outer edge // area of rim // weight of 1 washer Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 15

Case Study: Formulas • • Area of circle = radius 2 Radius of circle = diameter / 2 Rim area = area of outer circle - area of hole Unit weight = rim area thickness density Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 16

Listing 3. 4 Washer program Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 17

Listing 3. 4 Washer program (continued) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 18

Case Study: Testing Input data inner diameter of 1. 2 outer diameter of 2. 4 thickness of 0. 1 material density of 7. 87 quantity in batch of 1000 Should produce expected weight of batch of 2670. 23 grams Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 19

3. 2 Library Functions • Goals of software engineering – reliable code – accomplished by code reuse • C++ promotes code reuse with predefined classes and functions in the standard library Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 20

C++ cmath Library • Typical mathematical functions e. g. sqrt, sin, cos, log • Function use in an assignment statement Function call y = sqrt(x); Function name Function argument Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 21

Example: sqrt Function sqrt as a “black box” X is 16. 0 Square root function Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Result is 4. 0 22

Listing 3. 5 Illustration of the use of the C++ sqrt function Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 23

Listing 3. 5 Illustration of the use of the C++ sqrt function (continued) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 24

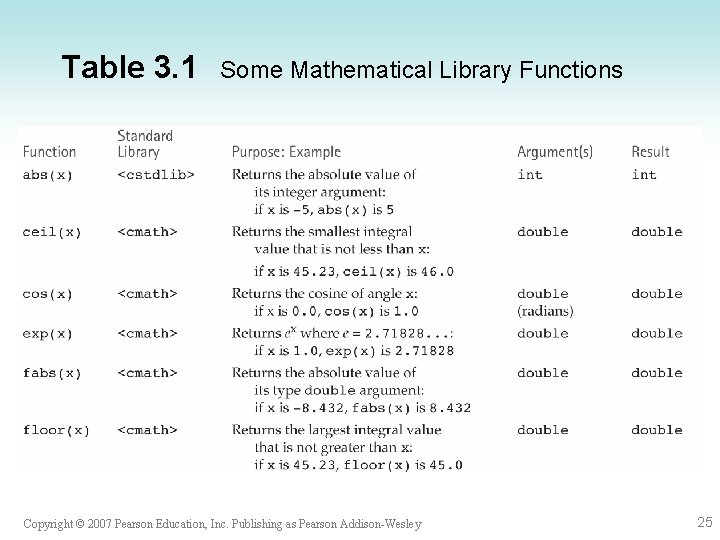
Table 3. 1 Some Mathematical Library Functions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 25

Table 3. 1 Some Mathematical Library Functions (continued) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 26

Looking Ahead • Could write own functions – find. Area( r ) returns area of circle of radius r – find. Circum( r ) returns circumference of circle of radius r • Program to compute area and circumference area = find. Area(radius); circum = find. Circum(radius); • Washers program rim. Area = find. Area(edge. Radius) find. Area(hole. Radius); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 27

3. 3 Top-Down Design and Structure Charts • Top-down design – process to break down complex problem into smaller, simpler subproblems – similar to development of an algorithm • Structure chart – graphical representation of relationship of subproblems Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 28

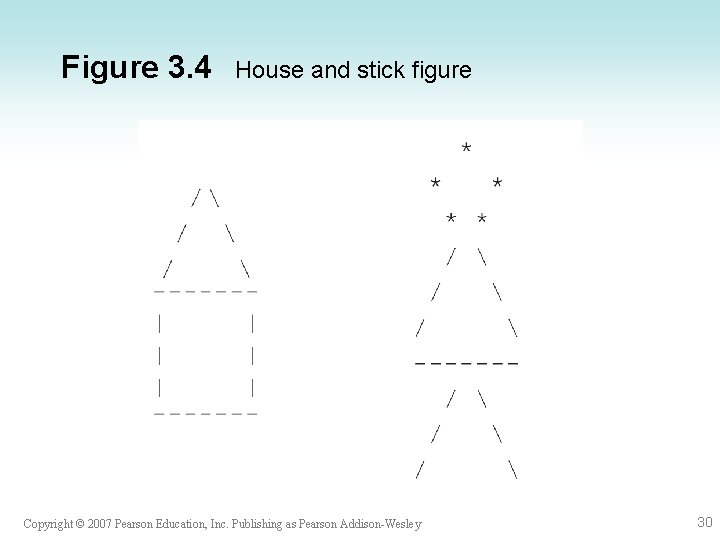
Case Study: Simple Figures • Problem statement Draw some simple diagrams on the screen, e. g. a house and a female stick figure. • Analysis – house is formed by displaying a triangle without its base, on top of a rectangle – stick figure consists of a circular shape, a triangle, and a triangle without its base. – 4 basic shapes: circle, base line, parallel lines, intersecting lines Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 29

Figure 3. 4 House and stick figure Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 30

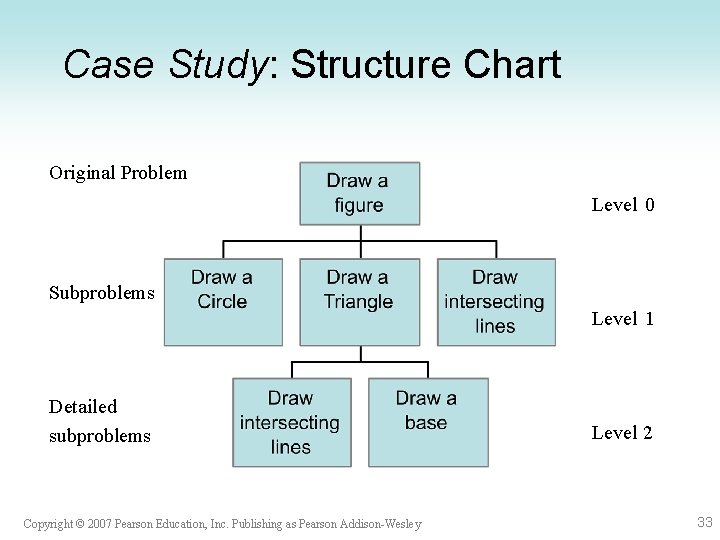
Case Study: Design - Algorithm • (no real data involved, so skip Data Requirements) • For stick figure: 1. Draw a circle. 2. Draw a triangle. 3. Draw intersecting lines. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 31

Case Study: Design - Algorithm • (no real data involved, so skip Data Requirements) • For stick figure: 1. Draw a circle. 2. Draw a triangle. 2. 1 Draw intersecting lines. 2. 2 Draw a base line. 3. Draw intersecting lines. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 32

Case Study: Structure Chart Original Problem Level 0 Subproblems Level 1 Detailed subproblems Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Level 2 33

3. 4 Functions without Arguments • • • Functions important part of top-down design main( ) is a function called by the OS Form of call: fname( ); Example: draw. Circle( ); Interpretation: the function fname is activated. After fname finishes execution, the program statement that follows the function call will be executed next. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 34

Some Notes on Functions • Don’t need to know details about how a function is implemented to know how to call. • E. g. y = sqrt(x); // don’t know how sqrt implemented • Do know how function is used (called). • Empty parentheses indicate no arguments (more on this later). Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 35

Function Prototype • Declares the function to the compiler • Appears before function main. • Tells compiler the function’s type, its name, and information about arguments. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 36

Function Prototype (no Arguments) • Form: ftype fname( ); • Example: void skip. Three( ); • Interpretation: identifier fname is declared to be the name of a function. The identifier ftype specifies the data type of the function result. Ftype of void indicates the function does not return a value. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 37

Function Definitions • Specifies the function’s operations • Function header similar to function prototype • Function body contains declarations for local variables and constants and executable statements • Prototypes precede main function (after #include directives) • Function definitions follow main function Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 38

Function Definition (no arguments) • Syntax: ftype fname( ) { local declarations executable statements } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 39

Function Definition (no arguments) • Example: // Displays block-letter H void print. H( ) { cout << “** **” << endl; cout << “******” << endl; cout << “** **” << endl; } // end print. H Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 40

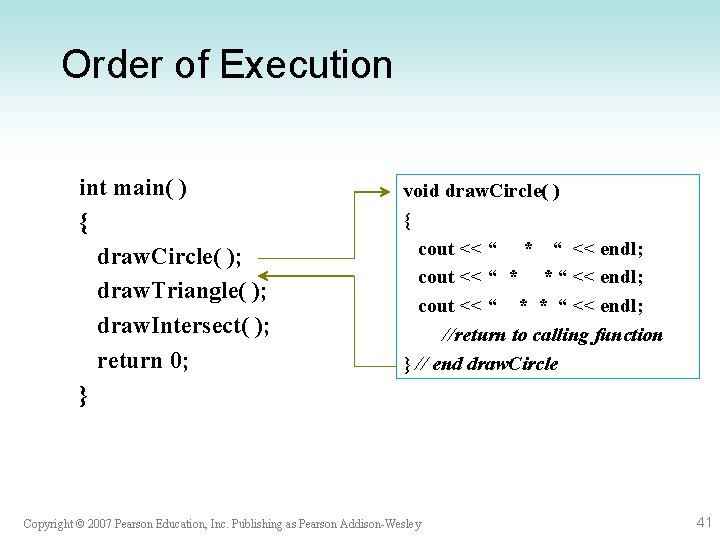
Order of Execution int main( ) { draw. Circle( ); draw. Triangle( ); draw. Intersect( ); return 0; } void draw. Circle( ) { cout << “ * “ << endl; cout << “ * * “ << endl; //return to calling function } // end draw. Circle Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 41

Notes on Function Execution • Execution always begins at first statement of main function • When a function is called – space is set aside for function variables – statements of function are executed – control returns to statement following call – function ends with space released Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 42

Function Advantages • • Team assignments on large project Simplify tasks Each function is a separate unit Top-down approach Reuse (e. g. draw. Triangle) Procedural abstraction Information hiding Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 43

Displaying User Instructions • Simple functions (no arguments, no return value) are of limited use • Useful for displaying instructions to user • E. g. void instruct( ); // prototype … instruct( ); //function call Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 44

Figure 3. 10 Function instruct // Displays instructions to user of area/circumference program void instruct () { cout << "This program computes the area and " << endl; cout << "circumference of a circle. " << endl; cout << "To use this program, enter the radius of the " << endl; cout << "circle after the prompt" << endl; cout << "Enter the circle radius: " << endl; cout << "The circumference will be computed in the same” << endl; cout << "units of measurement as the radius. The area " << endl; cout << "will be computed in the same units squared. " << endl; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 45

Functions with Input Arguments • Functions used like building blocks • Build systems one function at a time – E. g. stereo components • Use function arguments to carry information into function subprogram (input arguments) or to return multiple results (output arguments) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 46

Functions with Input Arguments • Arguments make functions versatile • E. g. : rim. Area = find. Area(edge. Radius) find. Area(hole. Radius); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 47

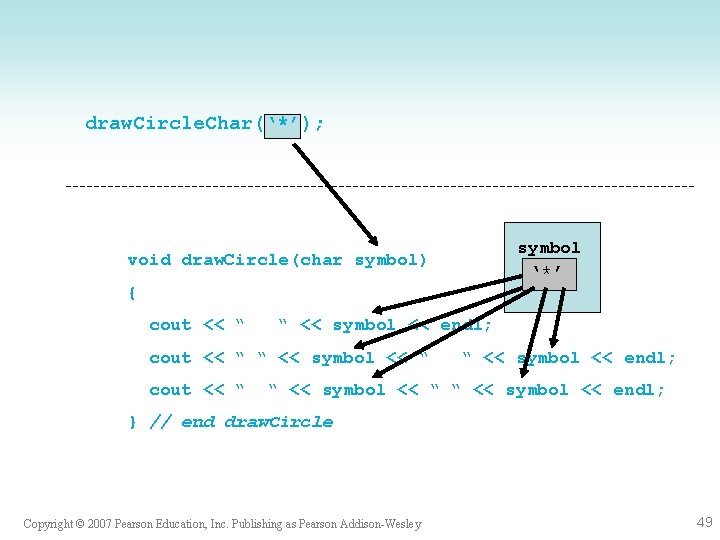
void Functions with Input Arguments • Give data to function to use • Don’t expect function to return any result(s) • Call format: fname (actual-argument-list); • E. g. : draw. Circle. Char(‘*’); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 48

draw. Circle. Char(‘*’); symbol void draw. Circle(char symbol) ‘*’ { cout << “ “ << symbol << endl; cout << “ “ << symbol << “ cout << “ “ << symbol << endl; “ << symbol << “ “ << symbol << endl; } // end draw. Circle Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 49

Functions with Arguments and a Single Result • Functions that return a result must have a return statement: Form: return expression; Example: return x * y; Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 50

#include <iostream> #include <cmath> using namespace std; const float PI = 3. 14159; float find. Circum(float); float find. Area(float); int main( ) { float radius = 10. 0; float circum; float area; circum = find. Circum(radius); area = find. Area(radius); cout << “Area is “ << area << endl; cout << “Circumference is “ << circum << endl; return 0; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 51

Figure 3. 12 Functions find. Circum and find. Area // Computes the circumference of a circle with radius r // Pre: r is defined and is > 0. // PI is a constant. // Post: returns circumference float find. Circum(float r) { return (2. 0 * PI * r); } // Computes the area of a circle with radius r // Pre: r is defined and is > 0. // PI is a constant. // Post: returns area float find. Area(float r) { return (PI * pow(r, 2)); } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 52

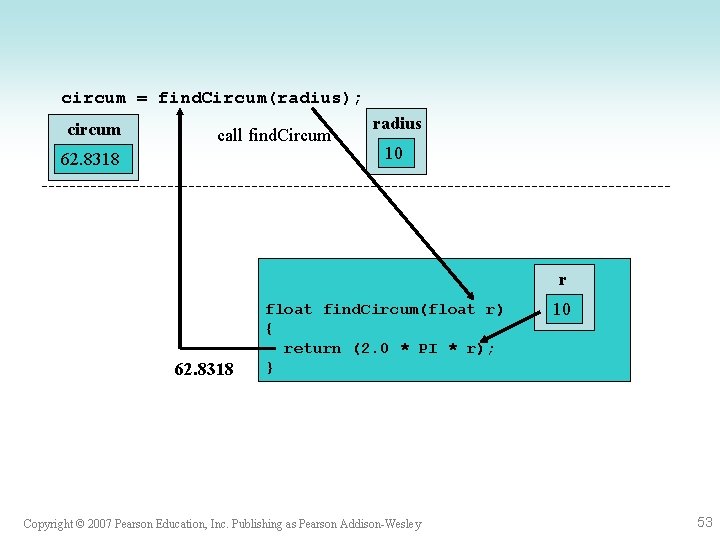
circum = find. Circum(radius); circum call find. Circum 62. 8318 radius 10 r 62. 8318 float find. Circum(float r) { return (2. 0 * PI * r); } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 10 53

Function Definition (Input Arguments with One Result) • Syntax: // function interface comment ftype fname(formal-parameter-declaration-list) { local variable declarations executable statements } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 54

Function Definition (Input Arguments with One Result) • Example: // Finds the cube of its argument. // Pre: n is defined. int cube(int n) { return (n * n); } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 55

Function Prototype (With Parameters) • Form: ftype fname(formal-parameter-type-list); • Example: int cube(int); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 56

Function Interface Comments • Preconditions – conditions that should be true before function is called – // Pre: r is defined • Postconditions – conditions that will be true when function completes execution – // Post: Returns circumference Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 57

Problem Inputs vs. Input Parameters • Problem inputs – variables that receive data from program user – through execution of input statement • Input parameters – receive data through execution of function call statement – must be defined before function is called Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 58

Listing 3. 14: Testing function test. Scale. cpp // File test. Scale. cpp // Tests function scale. #include <iostream> #include <cmath> using namespace std; // Function prototype float scale(float, int); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 59

Listing 3. 14: Testing function test. Scale. cpp (continued) int main() { float num 1; int num 2; // Get values for num 1 and num 2 cout << "Enter a real number: "; cin >> num 1; cout << "Enter an integer: "; cin >> num 2; // Call scale and display result. cout << "Result of call to function scale is " << scale(num 1, num 2) << endl; return 0; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 60

Listing 3. 14: Testing function test. Scale. cpp (continued) // Multiplies its first argument by the power of 10 // specified by its second argument. // Pre: x and n are defined and library cmath is // included float scale(float x, int n) { float scale. Factor; // local variable scale. Factor = pow(10, n); return (x * scale. Factor); } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 61

Listing 3. 14: Testing function test. Scale. cpp (continued) cout << "Result of call to function scale is " << scale(num 1, num 2) Actual arguments. << endl; . . Information flow float scale(float x, int n) Formal parameters { float scale. Factor; // local variable scale. Factor = pow(10, n); return (x * scale. Factor); } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 62

Argument/Parameter List Correspondence • Must have same number of actual arguments and formal parameters • Order of arguments in the lists determines correspondence • Each actual argument must be of a data type that is compatible to the corresponding formal parameter • The names of the actual arguments do not need to correspond to the formal parameters Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 63

Function Data Area • Each time function is executed – an area of memory is allocated for storage of the function’s data (formal parameters and local variables) – it is created empty with each call to the function • When the function terminates – the data area is lost Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 64

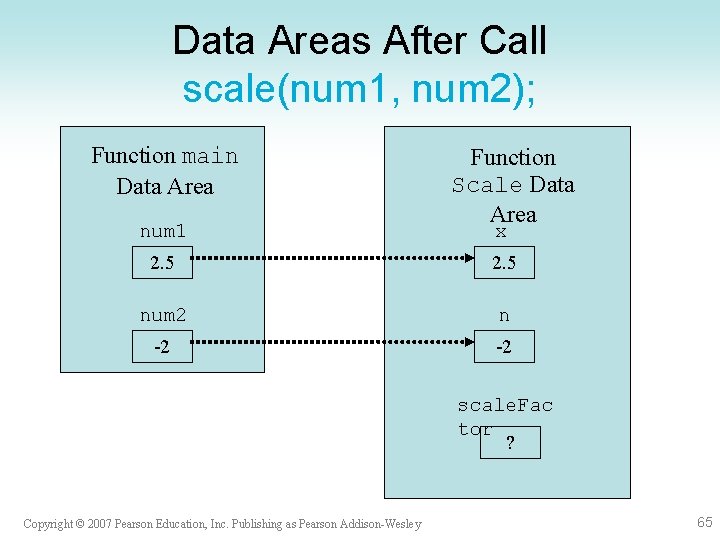
Data Areas After Call scale(num 1, num 2); Function main Data Area num 1 Function Scale Data Area x 2. 5 num 2 n -2 -2 scale. Fac tor ? Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 65

Testing Functions Using Drivers • Any function can be tested independently • Test driver – defines values for the function’s arguments – calls the function – displays the value returned for verification Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 66

Scope of Names • Scope - where a particular meaning of a name is visible or can be referenced • Local - can be referred to only within the one function – applies to • formal argument names • constants and variables declared within the function • Global - can be referred to within all functions – useful for constants – must be used with care Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 67

Listing 3. 15 Outline of program for studying scope of names Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 68

Using Class string • Data abstraction – facilitated in C++ through class feature – enables programmers to define new types – defines a set a values and a set of operations Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 69

Accessing the String Library • Must include the appropriate library #include <string> Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 70

String Objects • Attributes include – character sequence it stores – length • Common operations << >> = + Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 71

Listing 3. 16 Illustrating string operations Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 72

Listing 3. 16 Illustrating string operations (continued) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 73

Declaring string Objects • General declarations format: type identifier 1, identifier 2, . . . ; • E. g. : string first. Name, last. Name; string whole. Name; string greeting = “Hello “; Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 74

Reading and Displaying Strings • Extraction operator is defined for strings cin >> first. Name; // reads up to blank or return • Insertion operator is defined for strings cout << greetings << whole. Name << ‘!’ << endl; • Can read string with blanks getline(cin, last. Name, ; n’); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 75

String Assignment and Concatenation • + puts strings together (concatenates) • E. g. : whole. Name = first. Name + “ “ + last. Name; • Note need for space between names Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 76

Operator Overloading • Note use of + – usually means addition for two numeric values – has been redefined (overloaded) to also mean concatenation when applied to two strings • Useful when defining new types Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 77

Accessing String Operations • Member functions length and at • These functions can be called using dot notation • Applies the identified operation to the named object • E. g. : whole. Name. length( ) returns the length of the string currently stored in the variable whole. Name Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 78

Dot Notation • Syntax: • Ex: object. function-call first. Name. at(0) this returns the character in first. Name that is at position 0 (start numbering characters from left, beginning at 0). Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 79

Additional Member Functions • Searching for a string whole. Name. find(first. Name) • Inserting characters into a string whole. Name. insert(0, “Ms. ”); • Deleting portion of a string whole. Name. erase(10, 4); • Assign a substring to a string object title. assign(whole. Name, 0 3); Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 80

Introduction to Graphics • In normal computer output (called text mode), we use cout to display lines of characters to the standard output device, or console. • Now we discuss another mode of output (called graphics mode) that enables you to draw pictures or graphical patterns on your computer screen. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Windows and Pixels • In text mode, you don’t pay much attention to the position of each line of characters displayed on the screen. In graphics programming, you control the location in a window of each line or shape that you draw. Consequently, you must know your window size and how to reference the individual picture elements (called pixels) in a window. • You can visualize a window as an X-Y grid of pixels. If your window has the dimensions 400 x 300. The pixel at the topleft corner has X-Y coordinates (0, 0), and the pixel at the bottom-right corner has X-Y coordinates (399, 299). • Notice the pixels in the Y-direction are numbered differently from how we are accustomed. The Y-coordinate values increase as we move down the screen. In a normal X-Y coordinate system, the point (0, 0) is at the bottom-left corner, not the top-left corner. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Initializing a Window • A graphics program is a sequence of statements that call graphics functions to do the work. • Functions getmaxwidth and getmaxheight return the position of the last pixel in the X- and Y-directions on your computer screen. The statements bigx = getmaxwidth(); // get largest x-coordinate. bigy = getmaxheight(); // get largest y-coordinate. initwindow(bigx, bigy, "Full screen window - press a character to close window"); pop up a window of maximum width and height with the third argument as the window label (see Fig. 3. 13). The window position is set by the optional 4 th and 5 th arguments. If they are missing, the top-left corner of the window is at (0, 0). Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Listing 3. 17 Draw intersecting lines #include <graphics. h> #include <iostream> using namespace std; int main() { int bigx; int bigy; // largest x-coordinate // largest y-coordinate bigx = getmaxwidth(); // get largest x-coordinate bigy = getmaxheight(); // get largest y-coordinate initwindow(bigx, bigy, "Full screen window - press a key to close"); // Draw intersecting lines line(0, 0, bigx, bigy); // Draw white line from (0, 0) to ( bigx, bigy) setcolor(LIGHTGRAY); // Change color to gray line(bigx, 0, 0, bigy); // Draw gray line from ( bigx, 0) to (0, bigy) // Close screen when ready getch(); // pause until user presses a key closegraph(); // close the window // Display window size in console cout << "Window size is " << bigx << " X " << bigy << endl; return 0; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 84

Fig. 3. 13 Intersecting Lines Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 85

Listing 3. 18 Draw a House #include <graphics. h> int main() { // Define corners int x 1 = 100; int x 2 = 300; int x 3 = 500; int x 4 = 500; int x 5 = 325; int x 6 = 275; int of y 1 y 2 y 3 y 4 y 5 y 6 house = 200; = 100; = 200; = 400; = 325; // // // top-left corner roof peak top-right corner bottom-right corner of door top-left corner of door initwindow(640, 500, "House - press a key to close", 100, 50); // draw roof line(x 1, y 1, x 2, y 2); // Draw line from (x 1, y 1) to (x 2, y 2) line(x 2, y 2, x 3, y 3); // Draw line from (x 2, y 2) to (x 3, y 3) // draw rest of house. rectangle(x 1, y 1, x 4, y 4); // draw door. rectangle(x 5, y 5, x 6, y 6); getch(); closegraph(); return 0; // pause until user presses a key // close the window } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 86

Figure 3. 14 House Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 87

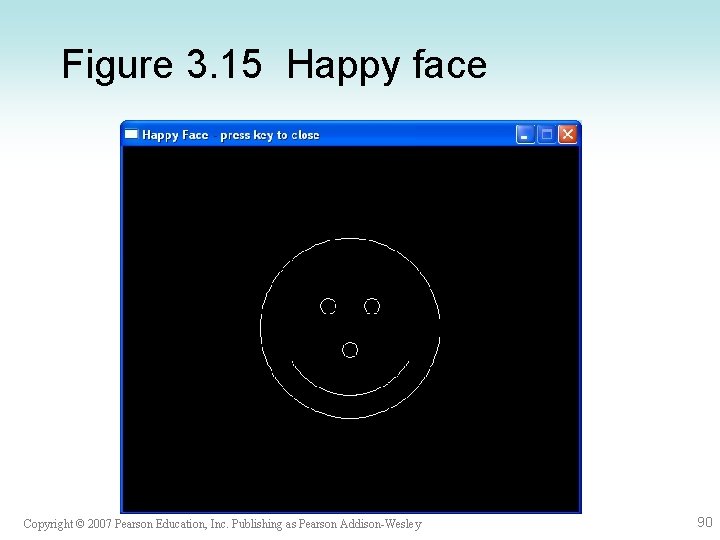
Listing 3. 19 Draw Happy Face #include <graphics. h> int main() { int mid. X, mid. Y, left. Eye. X, right. Eye. X, eye. Y, nose. X, nose. Y, head. Radius, eye. Nose. Radius, smile. Radius, step. X, step. Y; // // coordinates of center point eye center points nose center point head radius eye/nose radius smile radius x and y increments initwindow(500, 400, "Happy Face - press key to close", 200, 150); // draw head. mid. X = getmaxx() / 2; mid. Y = getmaxy() / 2; head. Radius = getmaxy() / 4; circle(mid. X, mid. Y, head. Radius); // // center head in x-direction center head in y-direction head will fill half the window draw head. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 88

Listing 3. 19 cont’d. // draw eyes. step. X = head. Radius / 4; step. Y = step. X; left. Eye. X = mid. X - step. X; right. Eye. X = mid. X + step. X; eye. Y = mid. Y - step. Y; eye. Nose. Radius = head. Radius / 10; circle(left. Eye. X, eye. Y, eye. Nose. Radius); circle(right. Eye. X, eye. Y, eye. Nose. Radius); // draw nose. X = mid. X; nose. Y = mid. Y + step. Y; circle(nose. X, nose. Y, eye. Nose. Radius); // // // x-offset for y-offset for x-coordinate y-coordinate eyes and nose for left eye for right eye for both eyes // draw left eye. // draw right eye. // nose is centered in x direction. // draw smile. Radius = int(0. 75 * head. Radius + 0. 5); arc(mid. X, mid. Y, 210, 330, smile. Radius); // 3/4 of head radius getch(); closegraph(); return 0; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 89

Figure 3. 15 Happy face Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 90

Listing 3. 20 Paint a House #include <graphics. h> int main() { // Insert same code as in Listing 3. 18 (Draw a house). . . // draw rest of house. rectangle(x 1, y 1, x 4, y 4); // Paint the house setfillstyle(HATCH_FILL, LIGHTGRAY); floodfill(x 2, y 2 + 10, WHITE); // Paint the roof setfillstyle(LINE_FILL, WHITE); floodfill(x 2, y 1 + 10, WHITE); // Paint the house setfillstyle(SOLID_FILL, BLUE); bar(x 5, y 5, x 6, y 6); // Draw blue door getch(); closegraph(); return 0; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 91

Figure 3. 16 Painted House Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Listing 3. 21 Draw Pirate #include <graphics. h> int main() { // Insert same code as in Listing 3. 19 (Draw Happy Face). . . // Draw nose. X = mid. X; nose. Y = mid. Y + step. Y; circle(nose. X, nose. Y, eye. Nose. Radius); // nose is centered in x direction // Draw frown smile. Radius = int(0. 75 * head. Radius + 0. 5); // 3/4 of head radius arc(mid. X, mid. Y + head. Radius, 65, 115, smile. Radius / 2); // Draw frown setfillstyle(CLOSE_DOT_FILL , WHITE); pieslice(mid. X, mid. Y, 10, 60, smile. Radius); // Draw eye patch outtextxy(getmaxx() / 3, getmaxy() - 20, "PIRATE WITH AN EYE PATCH"); getch(); closegraph(); return 0; } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 93

Fig. 3. 17 Pirate with eye patch Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley