Chapter 3 The Structure of Crystalline Solids Theoretical

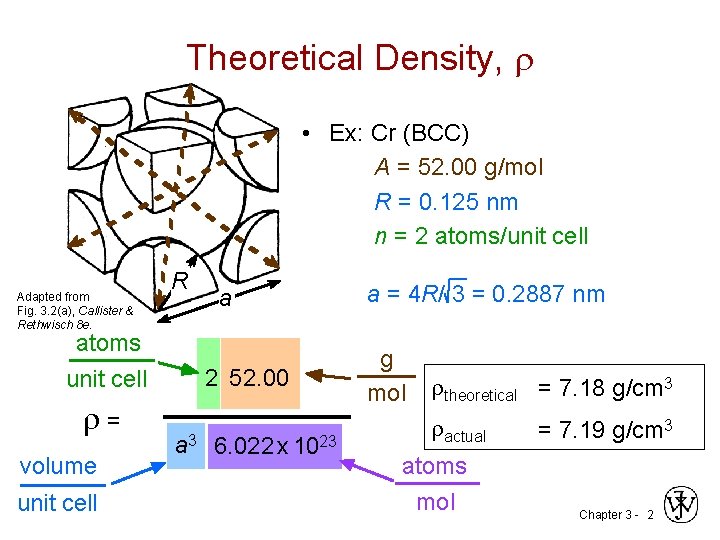
Chapter 3: The Structure of Crystalline Solids Theoretical Density, Density = = = Mass of Atoms in Unit Cell Total Volume of Unit Cell n A V C NA where n = number of atoms/unit cell A = atomic weight VC = Volume of unit cell = a 3 for cubic NA = Avogadro’s number = 6. 022 x 1023 atoms/mol Chapter 3 - 1

Theoretical Density, • Ex: Cr (BCC) A = 52. 00 g/mol R = 0. 125 nm n = 2 atoms/unit cell Adapted from Fig. 3. 2(a), Callister & Rethwisch 8 e. atoms unit cell = volume unit cell R a 2 52. 00 a 3 6. 022 x 1023 a = 4 R/ 3 = 0. 2887 nm g mol theoretical = 7. 18 g/cm 3 actual atoms mol = 7. 19 g/cm 3 Chapter 3 - 2

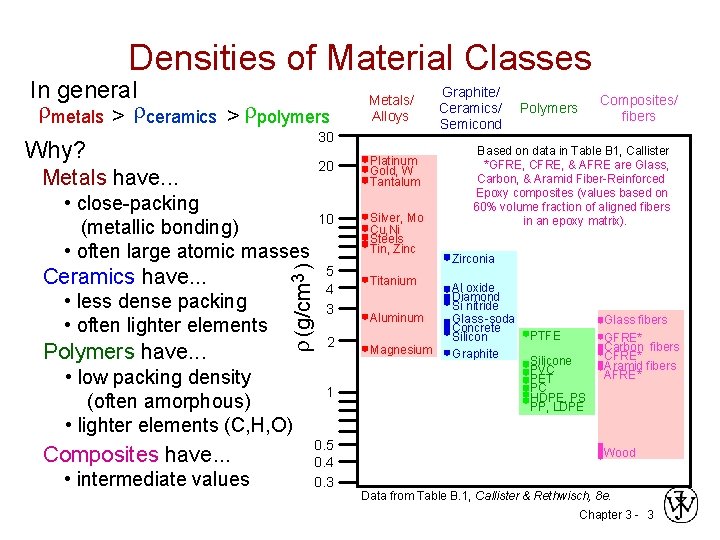
Densities of Material Classes In general metals > ceramics > polymers 30 Why? Ceramics have. . . 3 (g/cm ) Metals have. . . • close-packing (metallic bonding) • often large atomic masses • less dense packing • often lighter elements Polymers have. . . • low packing density (often amorphous) • lighter elements (C, H, O) Composites have. . . • intermediate values Metals/ Alloys 20 Platinum Gold, W Tantalum 10 Silver, Mo Cu, Ni Steels Tin, Zinc 5 4 3 2 1 0. 5 0. 4 0. 3 Graphite/ Ceramics/ Semicond Composites/ fibers Polymers Based on data in Table B 1, Callister *GFRE, CFRE, & AFRE are Glass, Carbon, & Aramid Fiber-Reinforced Epoxy composites (values based on 60% volume fraction of aligned fibers in an epoxy matrix). Zirconia Titanium Al oxide Diamond Si nitride Aluminum Glass -soda Concrete PTFE Silicon Magnesium Graphite Silicone PVC PET PC HDPE, PS PP, LDPE Glass fibers GFRE* Carbon fibers CFRE* Aramid fibers AFRE* Wood Data from Table B. 1, Callister & Rethwisch, 8 e. Chapter 3 - 3

Crystals as Building Blocks • Some engineering applications require single crystals: -- diamond single crystals for abrasives (Courtesy Martin Deakins, GE Superabrasives, Worthington, OH. Used with permission. ) -- turbine blades Fig. 8. 33(c), Callister & Rethwisch 8 e. (Fig. 8. 33(c) courtesy of Pratt and Whitney). • Properties of crystalline materials often related to crystal structure. -- Ex: Quartz fractures more easily along some crystal planes than others. (Courtesy P. M. Anderson) Chapter 3 - 4

Polycrystals • Most engineering materials are polycrystals. 1 mm • Nb-Hf-W plate with an electron beam weld. • Each "grain" is a single crystal. • If grains are randomly oriented, Anisotropic Adapted from Fig. K, color inset pages of Callister 5 e. (Fig. K is courtesy of Paul E. Danielson, Teledyne Wah Chang Albany) Isotropic overall component properties are not directional. • Grain sizes typically range from 1 nm to 2 cm (i. e. , from a few to millions of atomic layers). Chapter 3 - 5

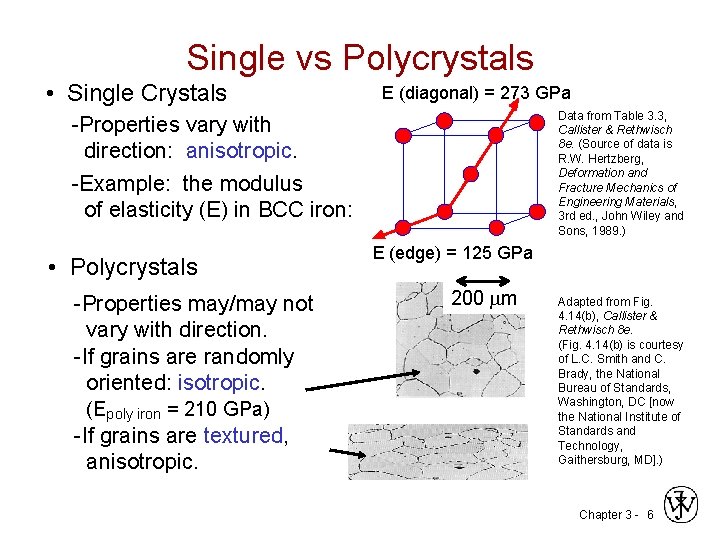
Single vs Polycrystals • Single Crystals E (diagonal) = 273 GPa Data from Table 3. 3, Callister & Rethwisch 8 e. (Source of data is R. W. Hertzberg, Deformation and Fracture Mechanics of Engineering Materials, 3 rd ed. , John Wiley and Sons, 1989. ) -Properties vary with direction: anisotropic. -Example: the modulus of elasticity (E) in BCC iron: • Polycrystals -Properties may/may not vary with direction. -If grains are randomly oriented: isotropic. (Epoly iron = 210 GPa) -If grains are textured, anisotropic. E (edge) = 125 GPa 200 mm Adapted from Fig. 4. 14(b), Callister & Rethwisch 8 e. (Fig. 4. 14(b) is courtesy of L. C. Smith and C. Brady, the National Bureau of Standards, Washington, DC [now the National Institute of Standards and Technology, Gaithersburg, MD]. ) Chapter 3 - 6

Polymorphism • Two or more distinct crystal structures for the same material. • Allotropy-when found in elemental solids. iron system titanium liquid , -Ti 1538ºC -Fe BCC carbon diamond, graphite FCC 1394ºC -Fe 912ºC BCC -Fe Chapter 3 - 7

Tin (Its Allotropic Transformation) White (or beta) tin, having a body-centered tetragonal crystal structure at room temperature, transforms, at 13. 2°C (55. 8°F), to gray (or alpha) tin, which has a crystal structure similar to diamond. The rate at which this change takes place is extremely slow; however, the lower the temperature (below 13. 2°C) the faster the rate. This transformation results in: Increase in volume (27 %), and, a decrease in density (from 7. 30 g/cm 3 to 5. 77 g/cm 3). Consequently, this volume expansion results in the disintegration of the white tin metal into a coarse powder of the gray allotrope. This produced some rather dramatic results in 1850 in Russia. The winter that year was particularly cold, and record low temperatures persisted for extended periods of time. The uniforms of some Russian soldiers had tin buttons, many of which crumbled because of these extreme cold conditions, as did also many of the tin church organ Chapter 3 - 8 pipes. This problem came to be known as the “tin disease. ”

3. 7 Iron has a BCC crystal structure, an atomic radius of 0. 124 nm, and an atomic weight of 55. 85 g/mol. Compute and compare its theoretical density with the experimental value found inside the front cover. 3. 8 Calculate the radius of an iridium atom, given that Ir has an FCC crystal structure, a density of 22. 4 g/cm 3, and an atomic weight of 192. 2 g/mol. Chapter 3 - 9

Crystal Systems Unit cell: smallest repetitive volume which contains the complete lattice pattern of a crystal. Fig. 3. 4, Callister & Rethwisch 8 e. a, b, and c are the lattice constant Chapter 3 - 10

Crystal Structure and Crystal System Q. What is the difference between crystal structure and crystal system? A: A crystal structure is described by both the geometry of, and atomic arrangements within, the unit cell, whereas a crystal system is described only in terms of the unit cell geometry. For example, face-centered cubic and bodycentered cubic are crystal structures that belong to the cubic crystal system. Chapter 3 - 11

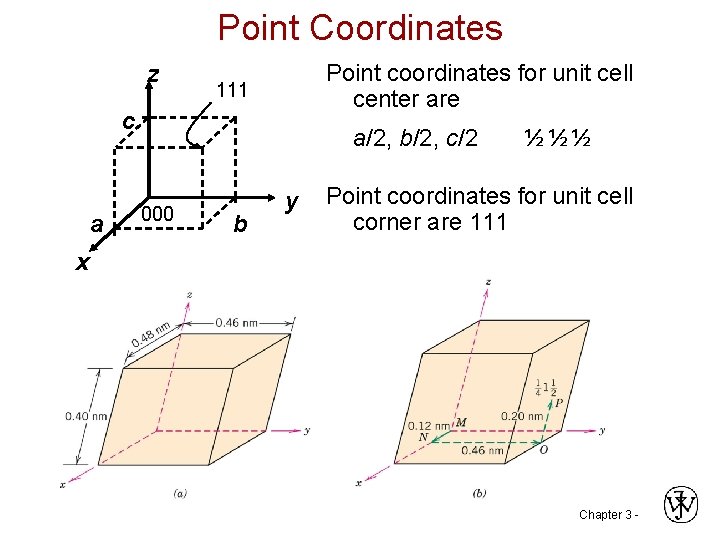
Point Coordinates z Point coordinates for unit cell center are 111 c a x a/2, b/2, c/2 ½ ½ ½ 000 b y Point coordinates for unit cell corner are 111 Chapter 3 -

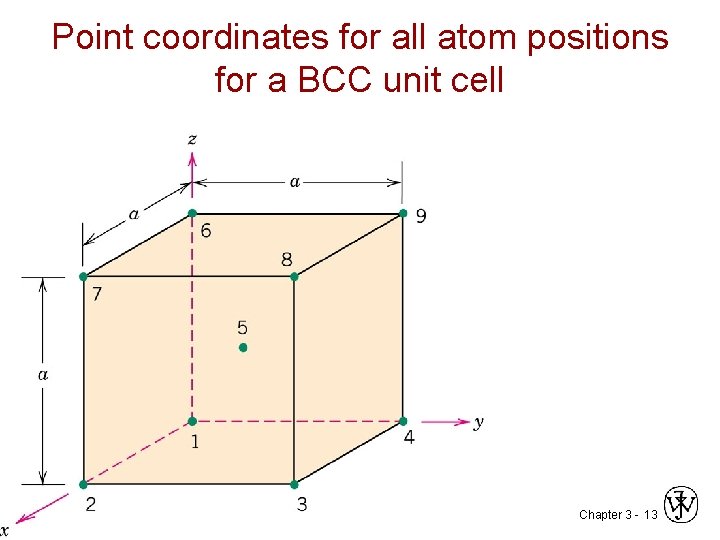
Point coordinates for all atom positions for a BCC unit cell Chapter 3 - 13

Crystallographic Directions Algorithm z y 1. Vector repositioned (if necessary) to pass through origin. 2. Read off projections in terms of unit cell dimensions a, b, and c 3. Adjust to smallest integer values 4. Enclose in square brackets, no commas [uvw] x ex: 1, 0, ½ => 2, 0, 1 => [ 201 ] -1, 1, 1 => [ 111 ] where overbar represents a negative index families of directions <uvw> Chapter 3 - 14

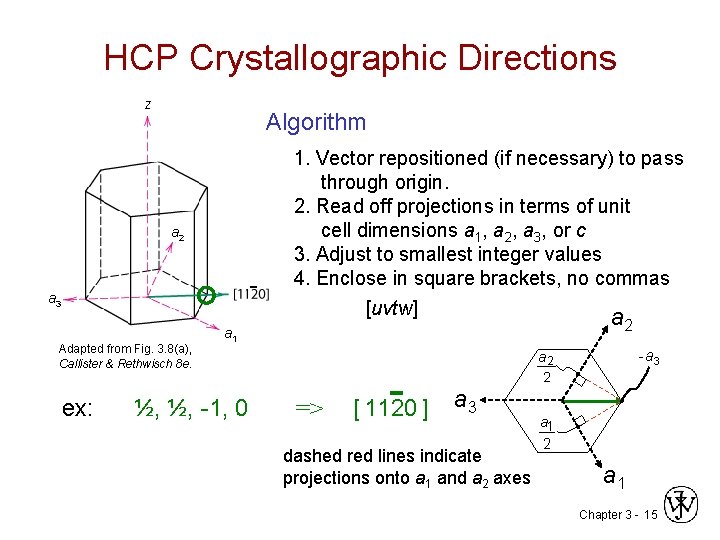
HCP Crystallographic Directions z Algorithm a 2 - a 3 Adapted from Fig. 3. 8(a), Callister & Rethwisch 8 e. a 1 1. Vector repositioned (if necessary) to pass through origin. 2. Read off projections in terms of unit cell dimensions a 1, a 2, a 3, or c 3. Adjust to smallest integer values 4. Enclose in square brackets, no commas [uvtw] a 2 -a 3 a 2 2 ex: ½, ½, -1, 0 => [ 1120 ] a 3 dashed red lines indicate projections onto a 1 and a 2 axes a 1 2 a 1 Chapter 3 - 15

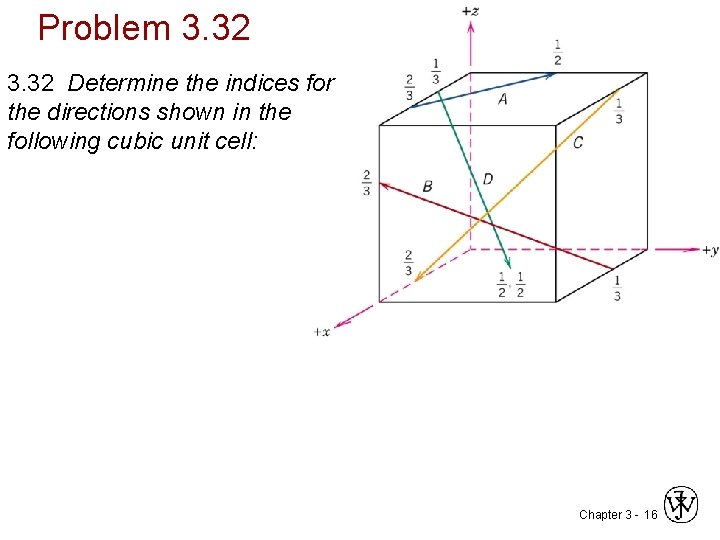
Problem 3. 32 Determine the indices for the directions shown in the following cubic unit cell: Chapter 3 - 16