Chapter 3 The Normal Distributions Density Curves Here

Chapter 3 The Normal Distributions

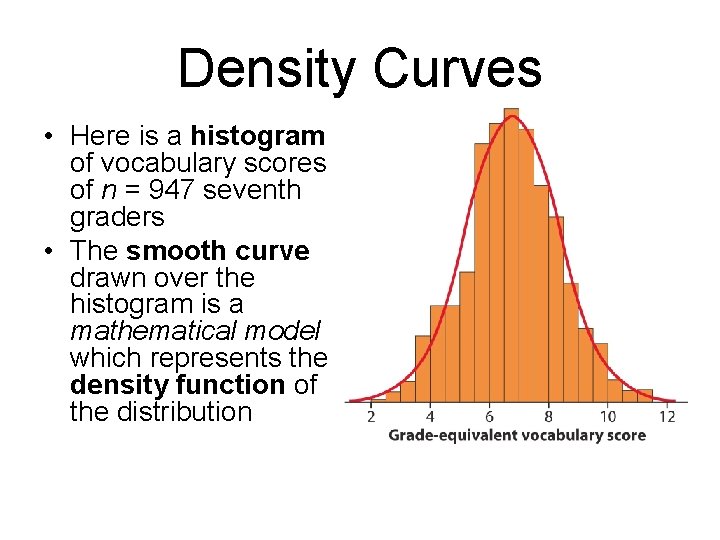
Density Curves • Here is a histogram of vocabulary scores of n = 947 seventh graders • The smooth curve drawn over the histogram is a mathematical model which represents the density function of the distribution

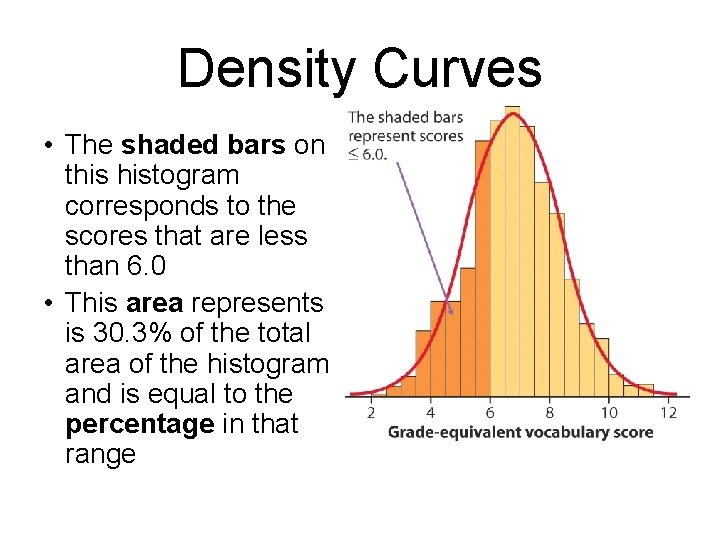
Density Curves • The shaded bars on this histogram corresponds to the scores that are less than 6. 0 • This area represents is 30. 3% of the total area of the histogram and is equal to the percentage in that range

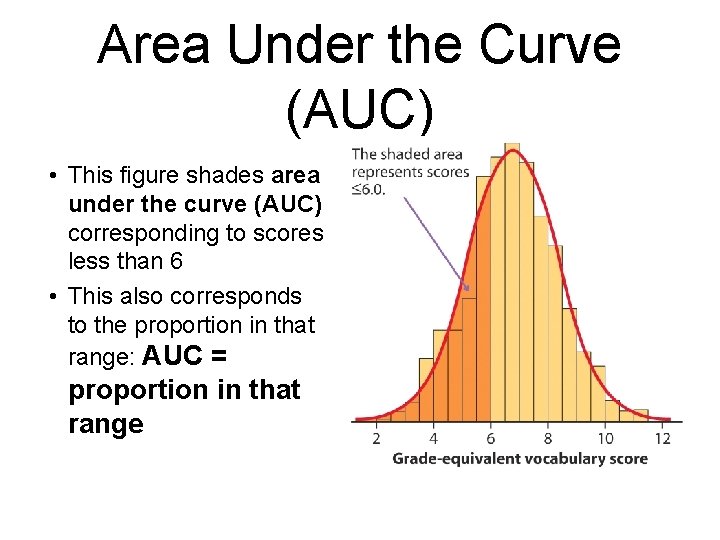
Area Under the Curve (AUC) • This figure shades area under the curve (AUC) corresponding to scores less than 6 • This also corresponds to the proportion in that range: AUC = proportion in that range

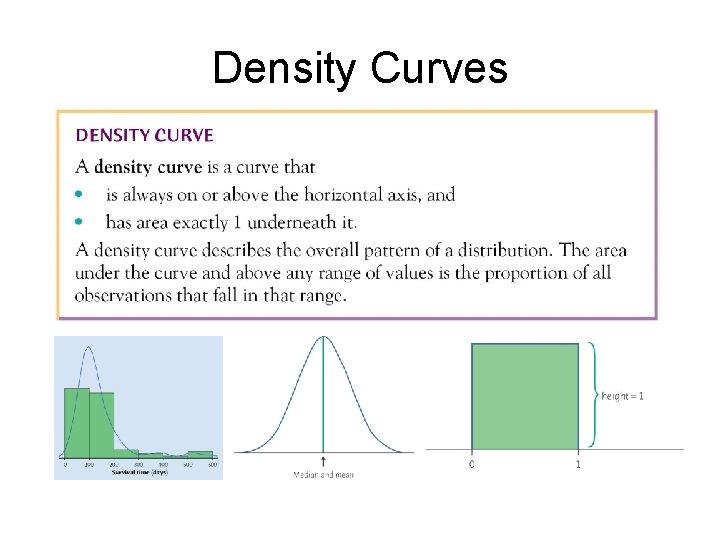
Density Curves

Mean and Median of Density Curve

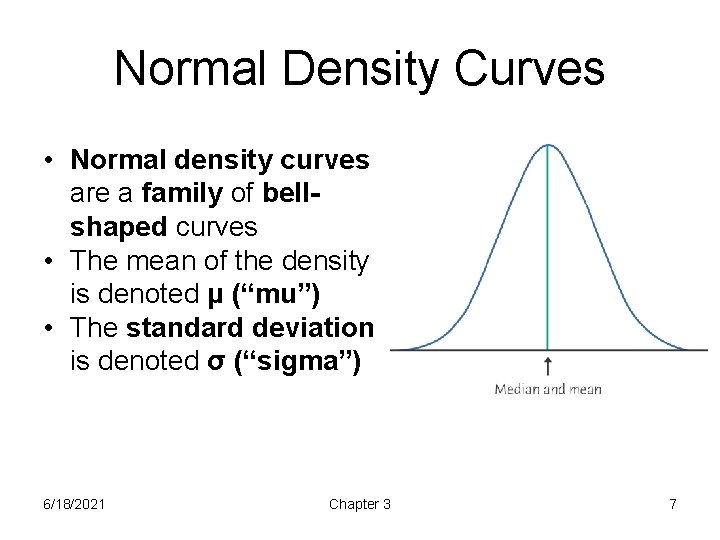
Normal Density Curves • Normal density curves are a family of bellshaped curves • The mean of the density is denoted μ (“mu”) • The standard deviation is denoted σ (“sigma”) 6/18/2021 Chapter 3 7

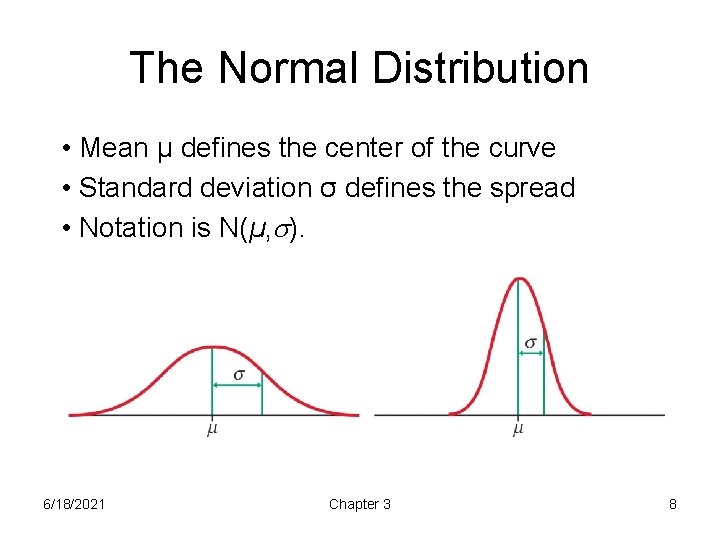
The Normal Distribution • Mean μ defines the center of the curve • Standard deviation σ defines the spread • Notation is N(µ, ). 6/18/2021 Chapter 3 8

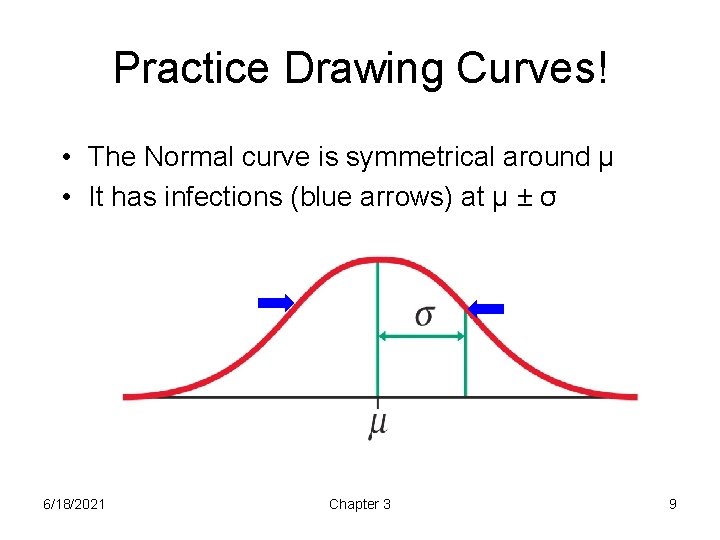
Practice Drawing Curves! • The Normal curve is symmetrical around μ • It has infections (blue arrows) at μ ± σ 6/18/2021 Chapter 3 9

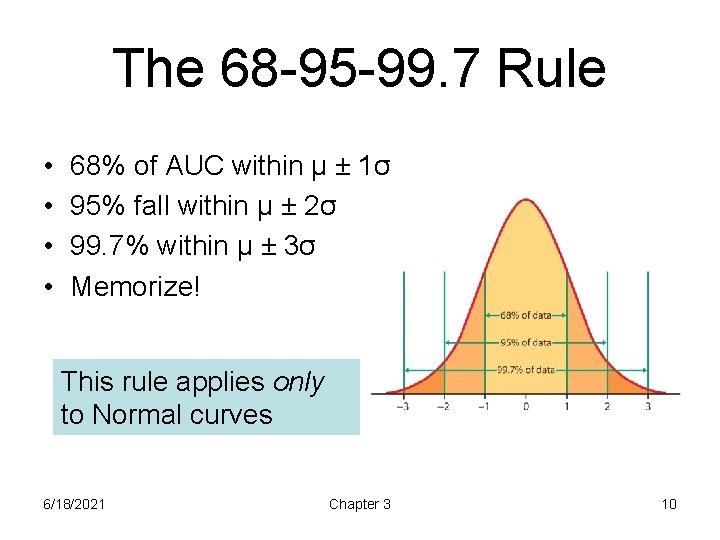
The 68 -95 -99. 7 Rule • • 68% of AUC within μ ± 1σ 95% fall within μ ± 2σ 99. 7% within μ ± 3σ Memorize! This rule applies only to Normal curves 6/18/2021 Chapter 3 10

Application of 68 -95 -99. 7 rule • Male height has a Normal distribution with μ = 70. 0 inches and σ = 2. 8 inches • Notation: Let X ≡ male height; X~ N(μ = 70, σ = 2. 8) 68 -95 -99. 7 rule • 68% in µ = 70. 0 2. 8 = 67. 2 to 72. 8 • 95% in µ 2 = 70. 0 2(2. 8) = 64. 4 to 75. 6 • 99. 7% in µ 3 = 70. 0 3(2. 8) = 61. 6 to 78. 4 6/18/2021 Chapter 3 11

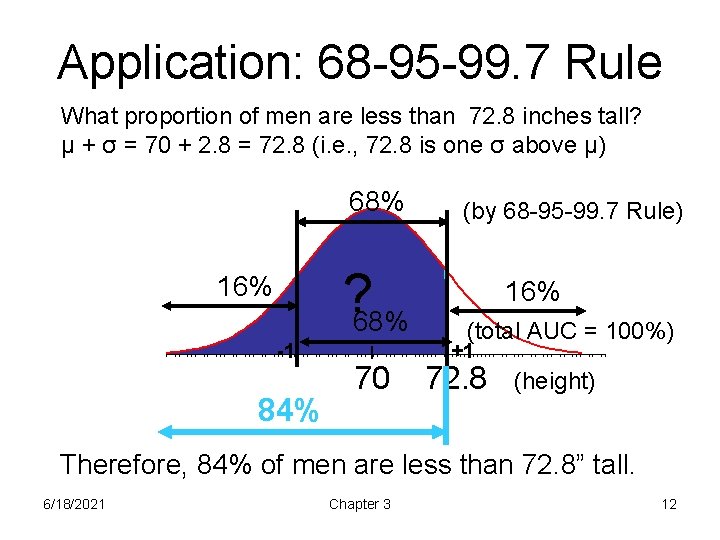
Application: 68 -95 -99. 7 Rule What proportion of men are less than 72. 8 inches tall? μ + σ = 70 + 2. 8 = 72. 8 (i. e. , 72. 8 is one σ above μ) 68% ? 68% 16% -1 84% 70 (by 68 -95 -99. 7 Rule) 16% (total AUC = 100%) +1 72. 8 (height) Therefore, 84% of men are less than 72. 8” tall. 6/18/2021 Chapter 3 12

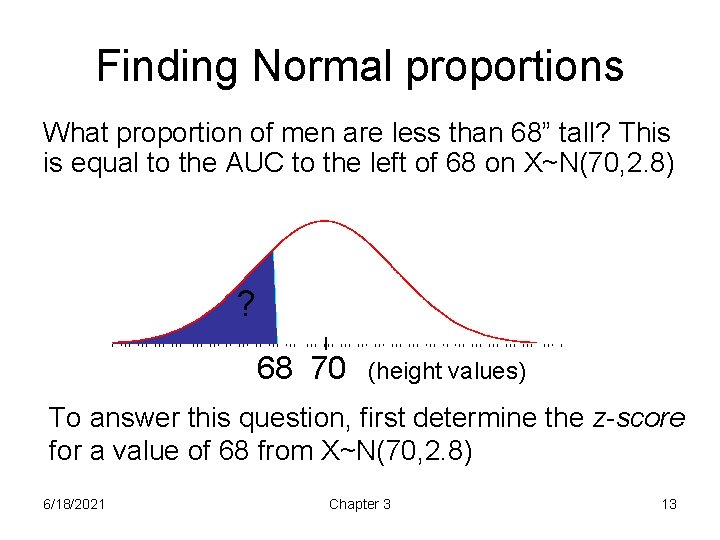
Finding Normal proportions What proportion of men are less than 68” tall? This is equal to the AUC to the left of 68 on X~N(70, 2. 8) ? 68 70 (height values) To answer this question, first determine the z-score for a value of 68 from X~N(70, 2. 8) 6/18/2021 Chapter 3 13

Z score • The z-score tells you how many standard deviation the value falls below (negative z score) or above (positive z score) mean μ • The z-score of 68 when X~N(70, 2. 8) is: Thus, 68 is 0. 71 standard deviations below μ. 6/18/2021 Chapter 3 14

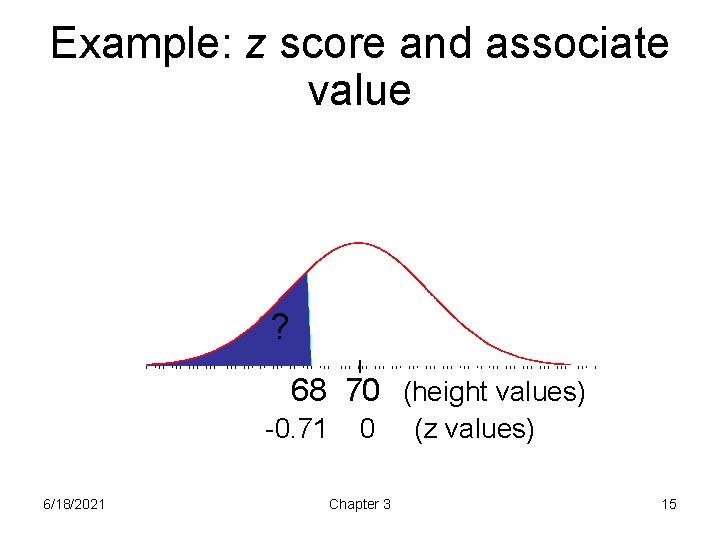
Example: z score and associate value ? 68 70 (height values) -0. 71 6/18/2021 0 Chapter 3 (z values) 15

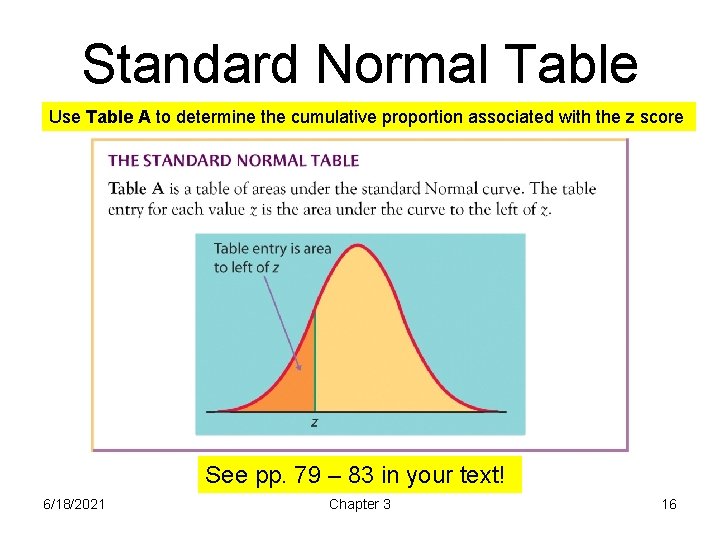
Standard Normal Table Use Table A to determine the cumulative proportion associated with the z score See pp. 79 – 83 in your text! 6/18/2021 Chapter 3 16

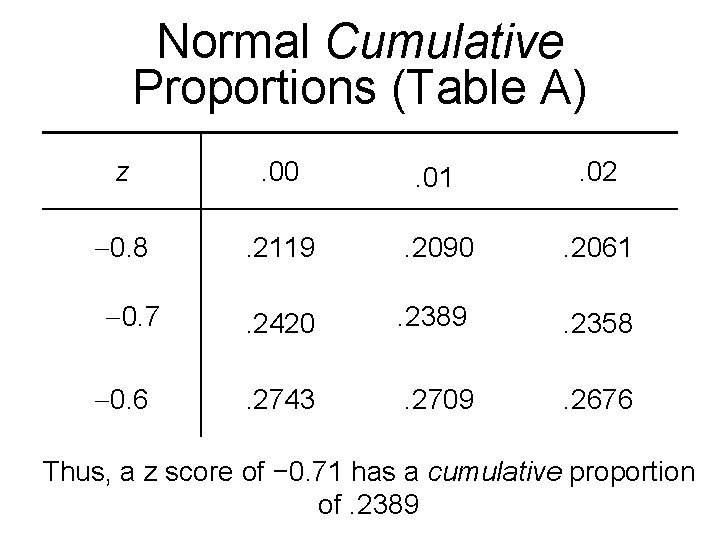
Normal Cumulative Proportions (Table A) z . 00 . 01 . 02 0. 8 . 2119 . 2090 . 2061 . 2420 . 2389 . 2358 . 2743 . 2709 . 2676 0. 7 0. 6 Thus, a z score of − 0. 71 has a cumulative proportion 6/18/2021 3 17 of. Chapter. 2389

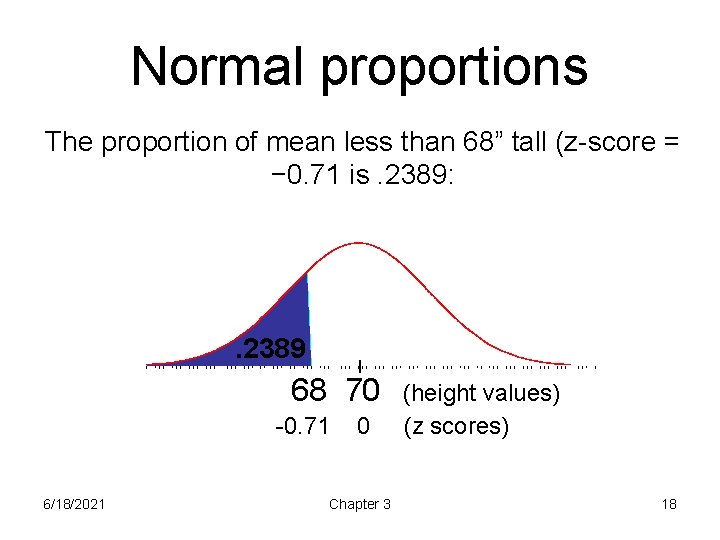
Normal proportions The proportion of mean less than 68” tall (z-score = − 0. 71 is. 2389: . 2389 68 70 -0. 71 6/18/2021 0 Chapter 3 (height values) (z scores) 18

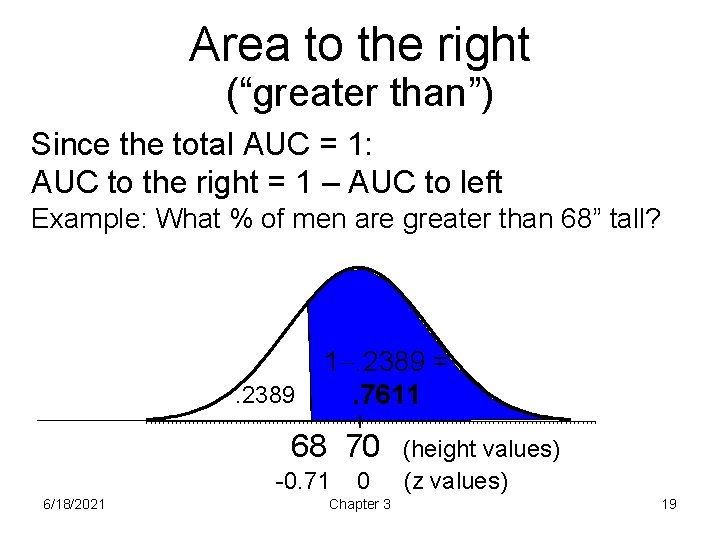
Area to the right (“greater than”) Since the total AUC = 1: AUC to the right = 1 – AUC to left Example: What % of men are greater than 68” tall? . 2389 1. 2389 =. 7611 68 70 -0. 71 6/18/2021 0 Chapter 3 (height values) (z values) 19

Normal proportions “The key to calculating Normal proportions is to match the area you want with the areas that represent cumulative proportions. If you make a sketch of the area you want, you will almost never go wrong. Find areas for cumulative proportions … from [Table A] (p. 79)” Follow the “method in the picture” (see pp. 79 – 80) to determine areas in right tails and between two points 6/18/2021 Chapter 3 20

Finding Normal values We just covered finding proportions for Normal variables. At other times, we may know the proportion and need to find the Normal value. Method for finding a Normal value: 1. State the problem 2. Sketch the curve 3. Use Table A to look up the proportion & z-score 4. Unstandardize the z-score with this formula 6/18/2021 Chapter 3 21

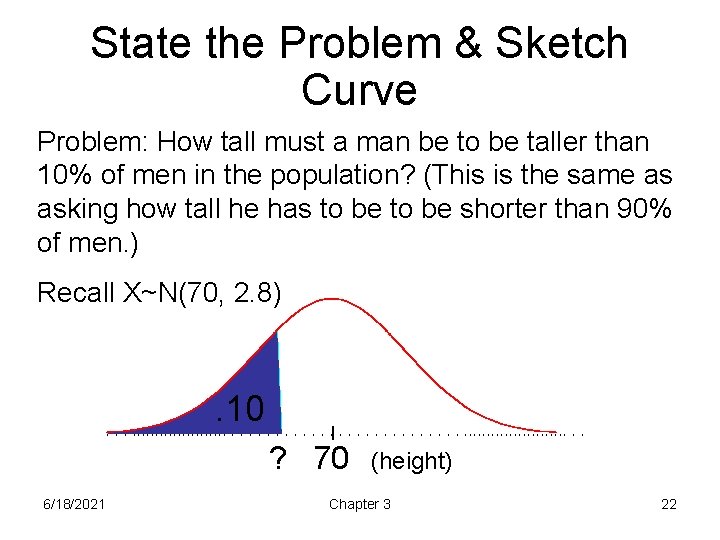
State the Problem & Sketch Curve Problem: How tall must a man be to be taller than 10% of men in the population? (This is the same as asking how tall he has to be shorter than 90% of men. ) Recall X~N(70, 2. 8) . 10 ? 70 6/18/2021 (height) Chapter 3 22

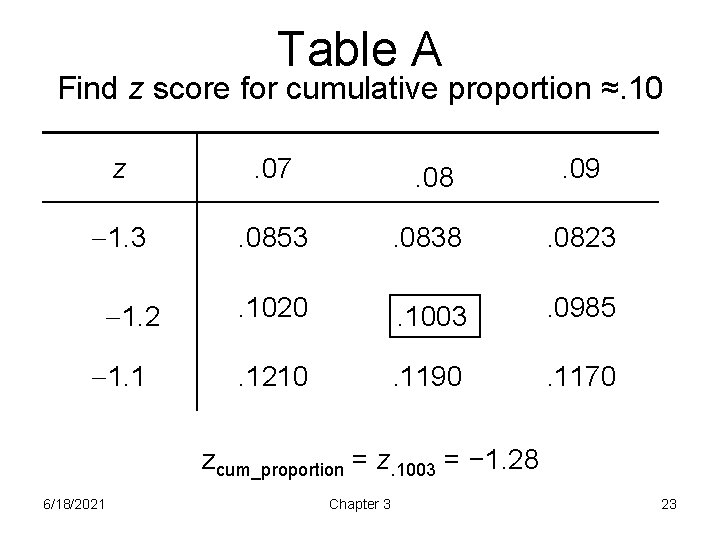
Table A Find z score for cumulative proportion ≈. 10 z . 07 . 08 . 09 1. 3 . 0853 . 0838 . 0823 . 1020 . 1003 . 0985 . 1210 . 1190 . 1170 1. 2 1. 1 zcum_proportion = z. 1003 = − 1. 28 6/18/2021 Chapter 3 23

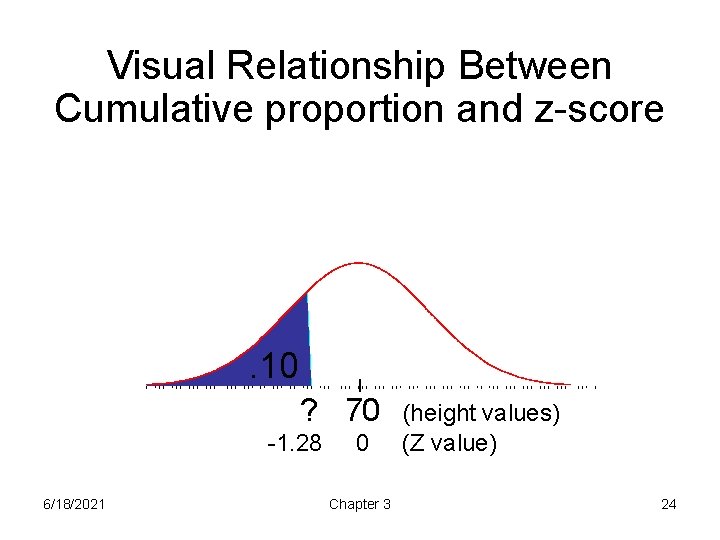
Visual Relationship Between Cumulative proportion and z-score . 10 ? 70 -1. 28 6/18/2021 0 Chapter 3 (height values) (Z value) 24

Unstandardize • x = μ + z∙σ = 70 + ( 1. 28 )(2. 8) = 70 + ( 3. 58) = 66. 42 • Conclude: A man would have to be less than 66. 42 inches tall to place him in the lowest 10% of heights 6/18/2021 Chapter 3 25