Chapter 3 The Karnough Map 3 1 Chapter

Chapter 3 The Karnough Map 3 1

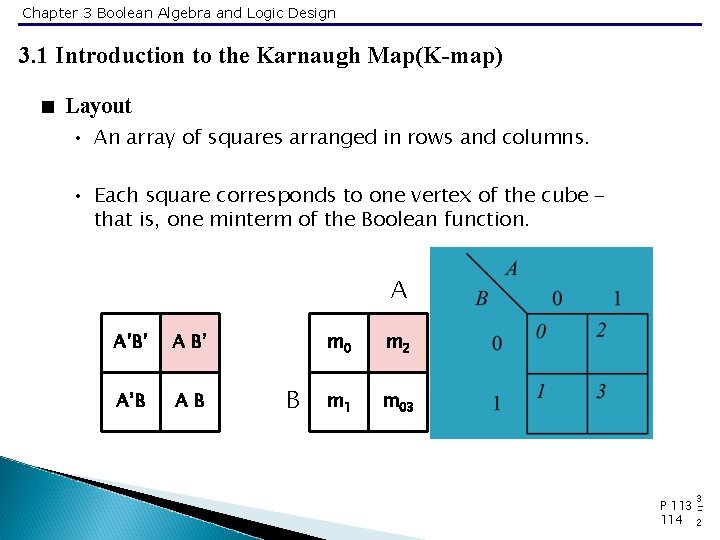
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Layout • An array of squares arranged in rows and columns. • Each square corresponds to one vertex of the cube that is, one minterm of the Boolean function. A A’B’ A’B AB B m 0 m 2 m 1 m 03 3 P 113 114 2

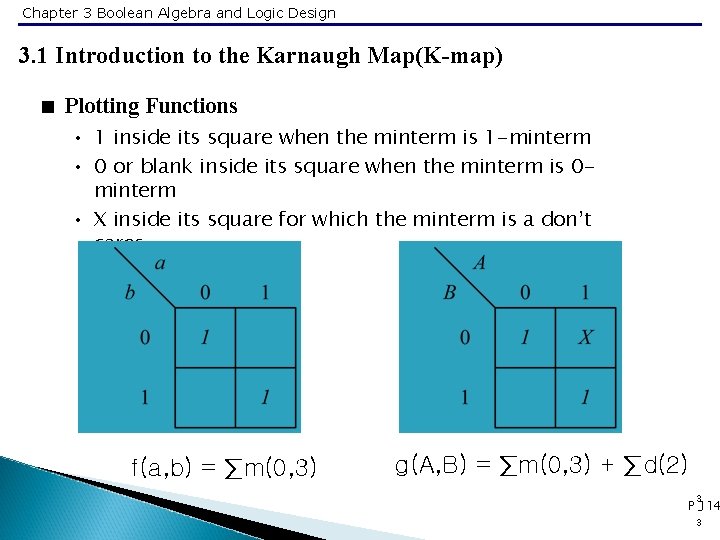
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Plotting Functions • 1 inside its square when the minterm is 1 -minterm • 0 or blank inside its square when the minterm is 0 minterm • X inside its square for which the minterm is a don’t cares. f(a, b) = ∑m(0, 3) g(A, B) = ∑m(0, 3) + ∑d(2) 3 P -114 3

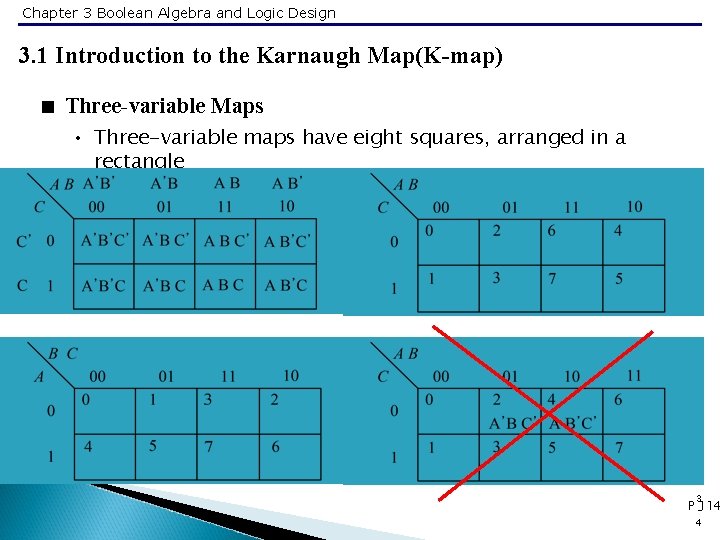
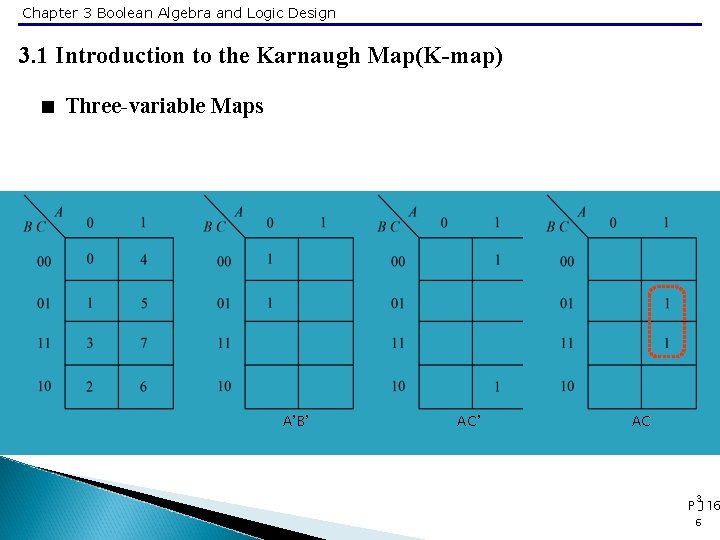
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Three-variable Maps • Three-variable maps have eight squares, arranged in a rectangle 3 P -114 4

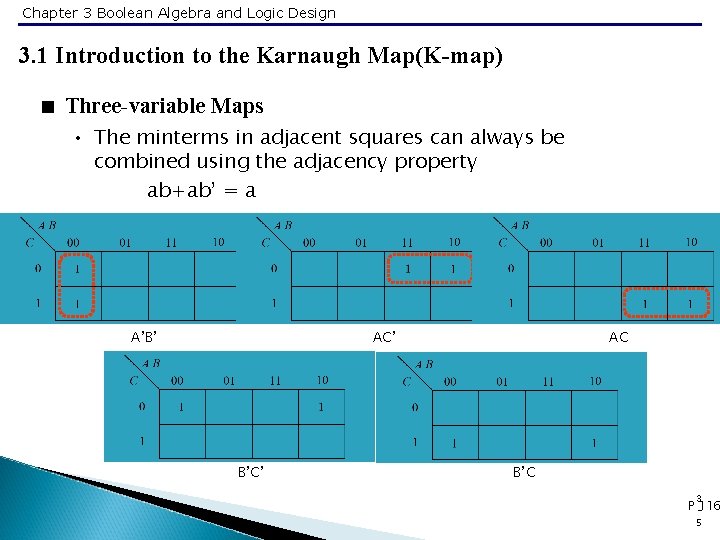
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Three-variable Maps • The minterms in adjacent squares can always be combined using the adjacency property ab+ab’ = a A’B’ AC’ B’C’ AC B’C 3 P -116 5

Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Three-variable Maps A’B’ AC 3 P -116 6

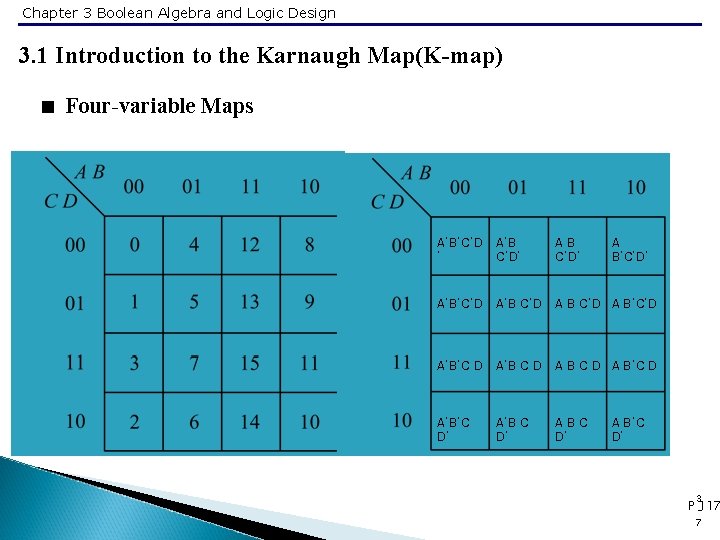
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Four-variable Maps A’B’C’D ’ A’B C’D’ A B’C’D’ A’B’C’D A’B C’D A B’C’D A’B’C D A’B C D A B’C D A’B’C D’ A’B C D’ ABC D’ A B’C D’ 3 P -117 7

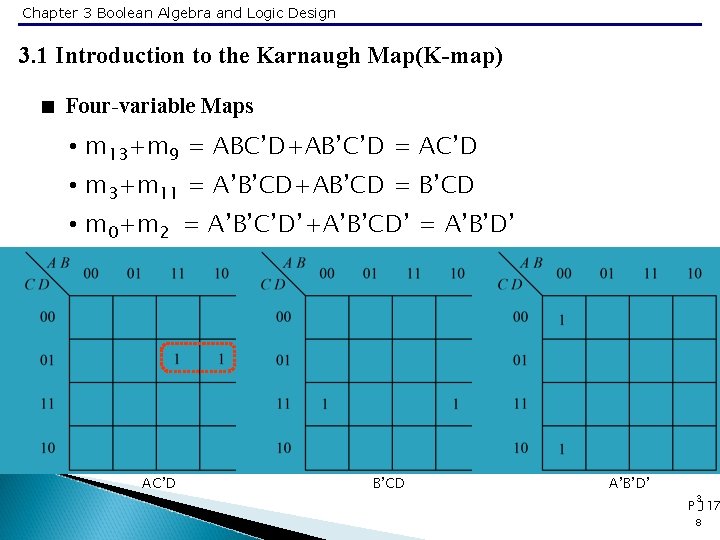
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Four-variable Maps • m 13+m 9 = ABC’D+AB’C’D = AC’D • m 3+m 11 = A’B’CD+AB’CD = B’CD • m 0+m 2 = A’B’C’D’+A’B’CD’ = A’B’D’ AC’D B’CD A’B’D’ 3 P -117 8

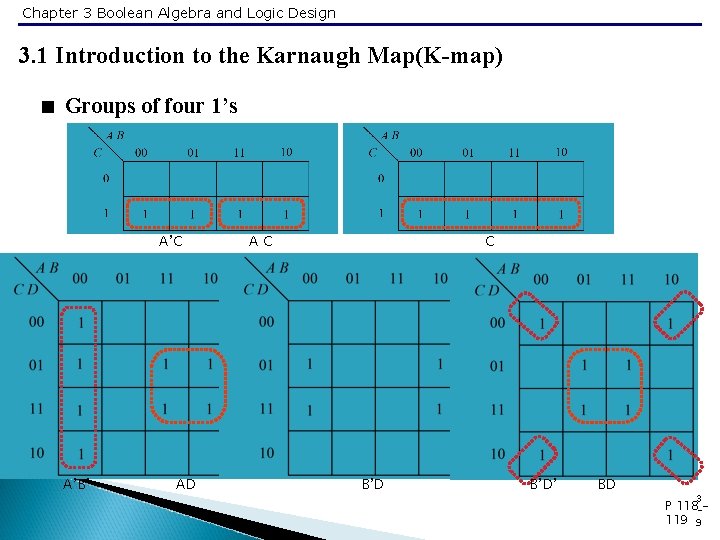
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Groups of four 1’s A’C A’B’ AD AC C B’D’ BD 3 P 118 -119 9

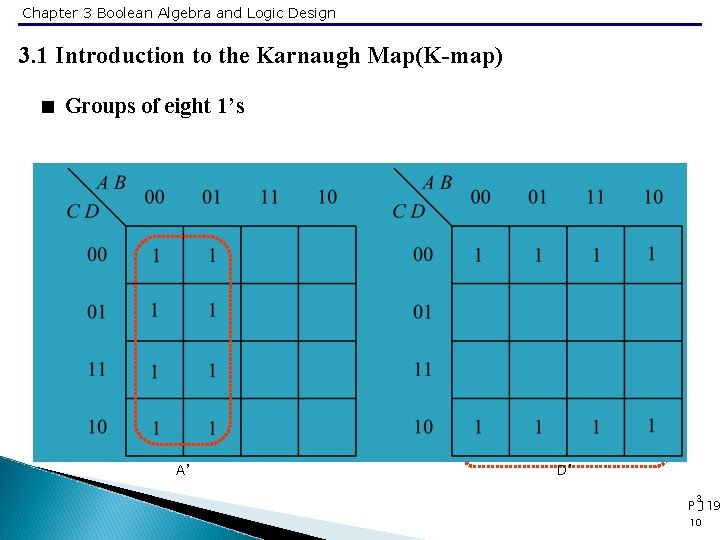
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Groups of eight 1’s A’ D’ 3 P -119 10

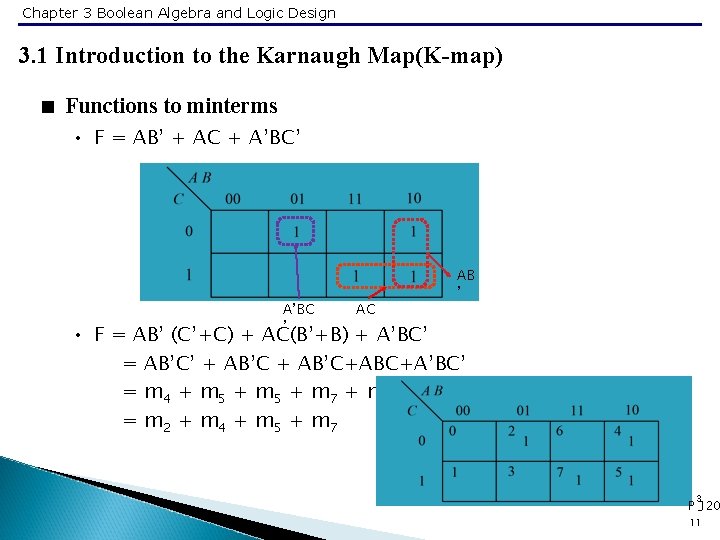
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < Functions to minterms • F = AB’ + AC + A’BC’ A’BC ’ AC AB ’ • F = AB’ (C’+C) + AC(B’+B) + A’BC’ = AB’C’ + AB’C+ABC+A’BC’ = m 4 + m 5 + m 7 + m 2 = m 2 + m 4 + m 5 + m 7 3 P -120 11

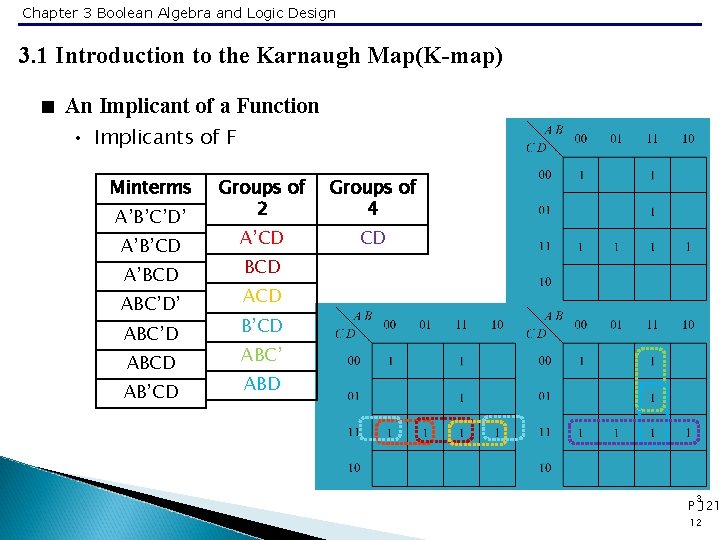
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < An Implicant of a Function • Implicants of F Minterms A’B’C’D’ A’B’CD A’BCD ABC’D’ ABC’D ABCD AB’CD Groups of 2 Groups of 4 A’CD CD BCD ACD B’CD ABC’ ABD 3 P -121 12

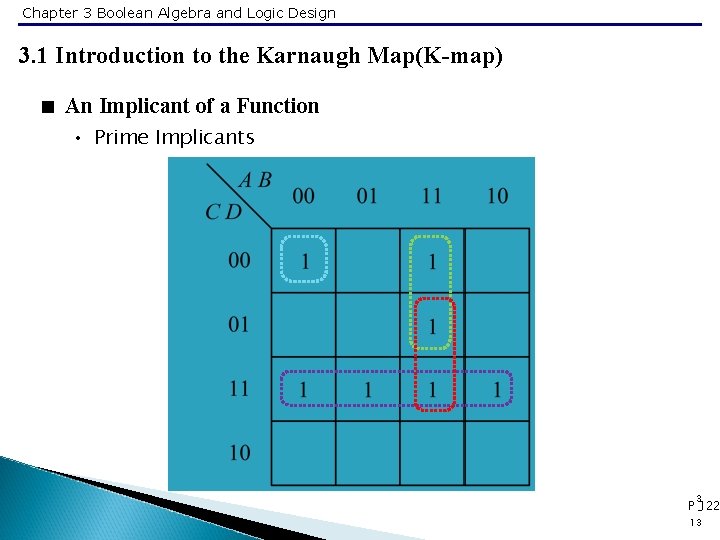
Chapter 3 Boolean Algebra and Logic Design 3. 1 Introduction to the Karnaugh Map(K-map) < An Implicant of a Function • Prime Implicants 3 P -122 13

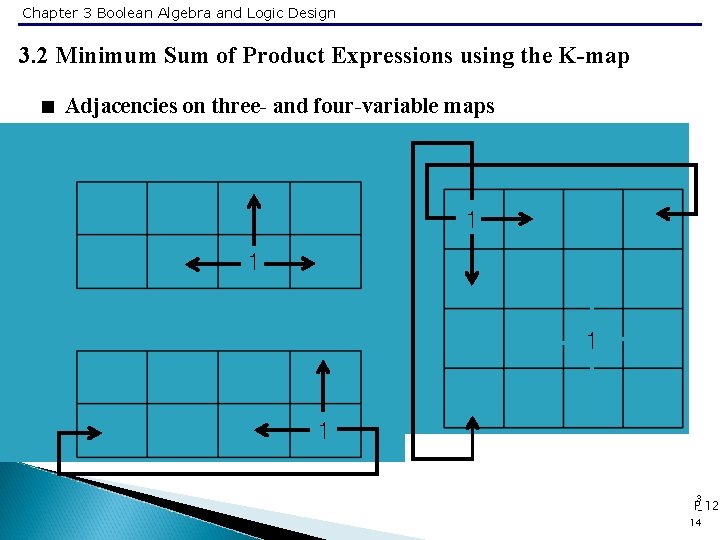
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Adjacencies on three- and four-variable maps 1 1 3 P- 123 14

Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Map Method 1 1. Find all essential prime implicants. Circle them on the map and mark the minterm(s) that make them essential with a star(*). Do this by examining each 1 on the map that has not already been circled. It is usually quickest to start with the most isolated 1’s, that is, those that have the fewest adjacent squares with 1’s in them. 2. Find enough other prime implicants to cover the function. Do this using two criteria : a. Choose a prime implicant that covers as many new 1’s(that is, those not already covered by a chosen prime implicant). b. Avoid leaving isolated uncovered 1’s. 3 15

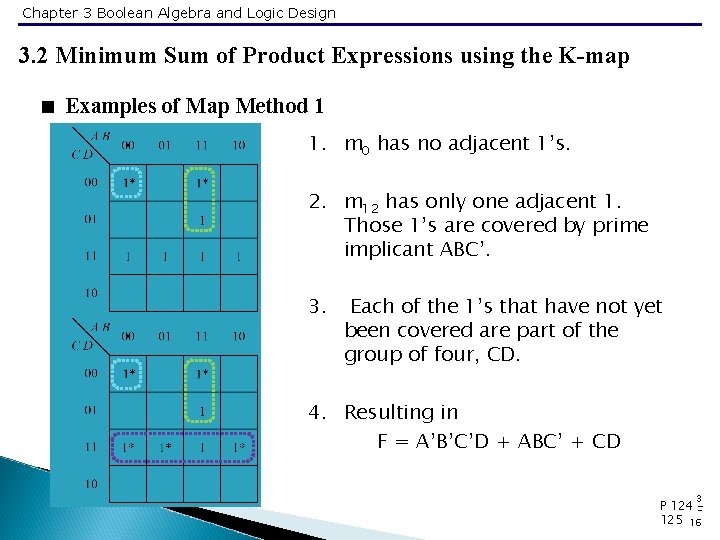
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Examples of Map Method 1 1. m 0 has no adjacent 1’s. 2. m 12 has only one adjacent 1. Those 1’s are covered by prime implicant ABC’. 3. Each of the 1’s that have not yet been covered are part of the group of four, CD. 4. Resulting in F = A’B’C’D + ABC’ + CD 3 P 124 125 16

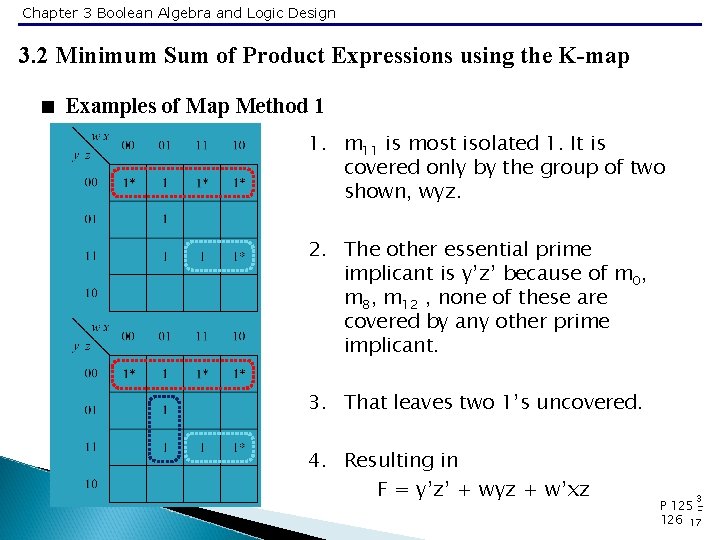
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Examples of Map Method 1 1. m 11 is most isolated 1. It is covered only by the group of two shown, wyz. 2. The other essential prime implicant is y’z’ because of m 0, m 8, m 12 , none of these are covered by any other prime implicant. 3. That leaves two 1’s uncovered. 4. Resulting in F = y’z’ + wyz + w’xz 3 P 125 126 17

Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Example of “dead end” • f = a’b’c + a’bc’ + a’bc + ab’c’ • We grouped the first two minterms. But, the two 1’s that are left could not be combined, and resulted in a three-term solution. • If we use the map, we could see that choosing the two essential prime implicants on the right-hand map includes all of the minterms and produces the solution. f = a’b + b’c 3 P -126 18

Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Produce a Minimum Solution • f(a, b, c, d) = ∑m(0, 2, 4, 6, 7, 8, 9, 11, 12, 14) • Only one 1(m 8) is not covered by an essential prime implicant. It can be covered in two ways : groupwith of four, • The group of four provides a solution one group less of two literal. f = a’d’ + bd’ + a’bc + ab’d + c’d’ 3 P -127 19

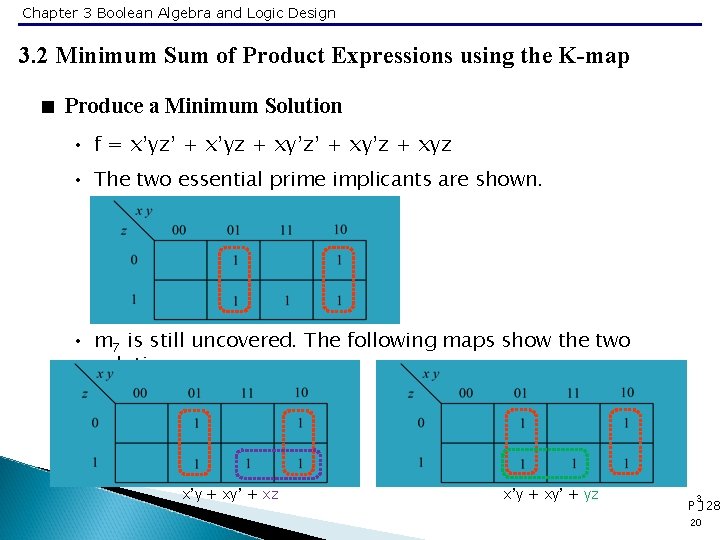
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Produce a Minimum Solution • f = x’yz’ + x’yz + xy’z’ + xy’z + xyz • The two essential prime implicants are shown. • m 7 is still uncovered. The following maps show the two solutions. x’y + xy’ + xz x’y + xy’ + yz 3 P -128 20

Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Produce a Minimum Solution • g(w, x, y, z) = ∑m(2, 5, 6, 7, 9, 10, 11, 13, 15) • m 14 is left could not be combined. • Three Solutions 1. g = xz + w’yz’ + wx’y 2. g = xz + w’yz’ + x’yz’ 3. g = xz + wz + x’yz’ + w’zy 3 P -129 21

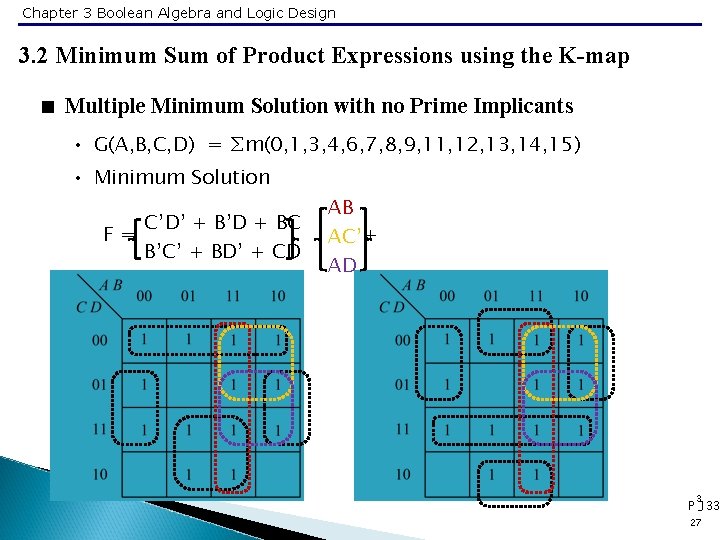
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Multiple Minimum Solution 1 • Don’t be greedy. • Minimum Solution G = A’BC’ + A’CD + ABC + AC’D 3 P -129 22

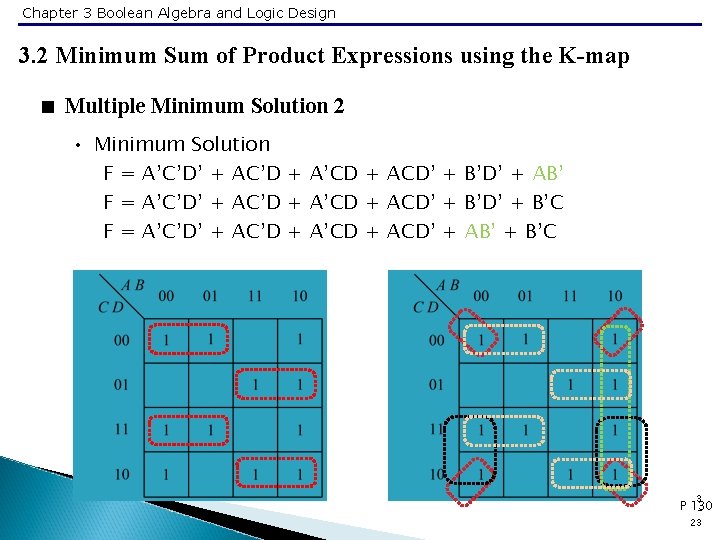
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Multiple Minimum Solution 2 • Minimum Solution F = A’C’D’ + AC’D + A’CD + ACD’ + B’D’ + AB’ F = A’C’D’ + AC’D + A’CD + ACD’ + B’C F = A’C’D’ + AC’D + A’CD + ACD’ + AB’ + B’C 3 P 130 23

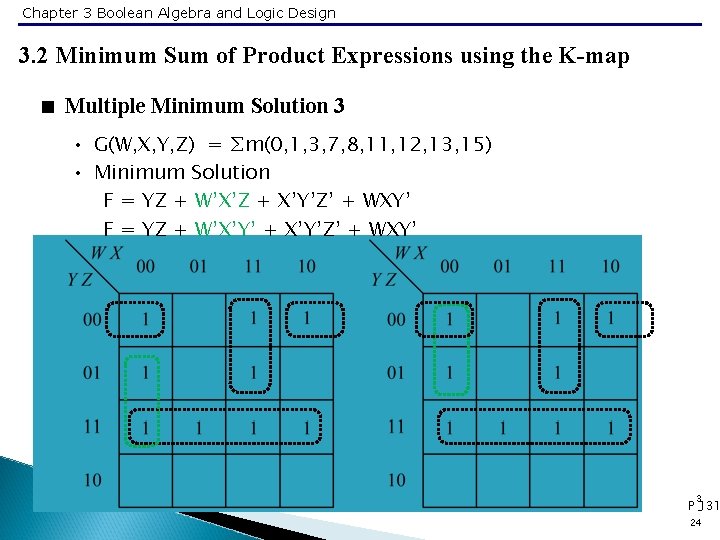
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Multiple Minimum Solution 3 • G(W, X, Y, Z) = ∑m(0, 1, 3, 7, 8, 11, 12, 13, 15) • Minimum Solution F = YZ + W’X’Z + X’Y’Z’ + WXY’ F = YZ + W’X’Y’ + X’Y’Z’ + WXY’ 3 P -131 24

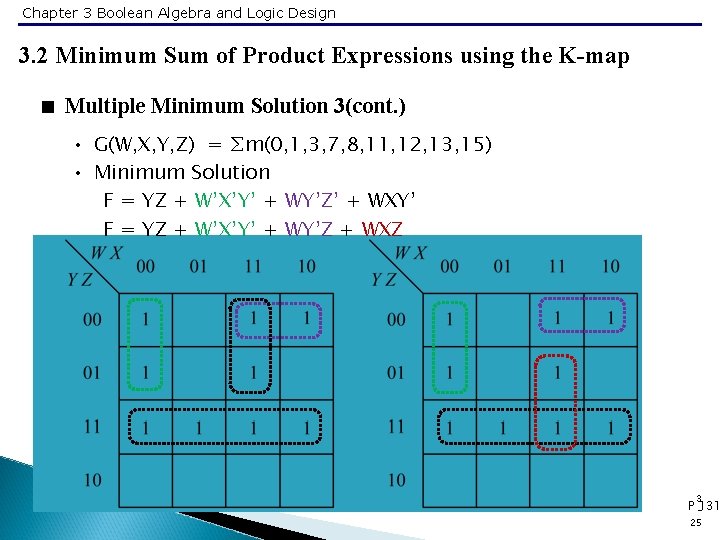
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Multiple Minimum Solution 3(cont. ) • G(W, X, Y, Z) = ∑m(0, 1, 3, 7, 8, 11, 12, 13, 15) • Minimum Solution F = YZ + W’X’Y’ + WY’Z’ + WXY’ F = YZ + W’X’Y’ + WY’Z + WXZ 3 P -131 25

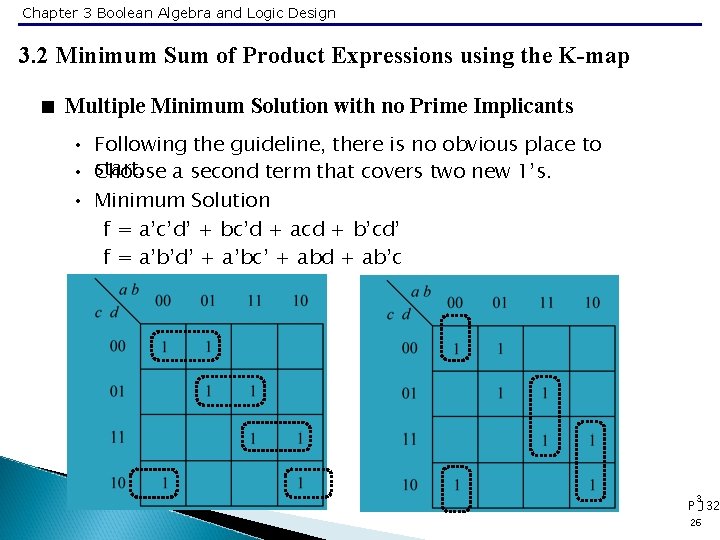
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Multiple Minimum Solution with no Prime Implicants • • • Following the guideline, there is no obvious place to start. Choose a second term that covers two new 1’s. Minimum Solution f = a’c’d’ + bc’d + acd + b’cd’ f = a’b’d’ + a’bc’ + abd + ab’c 3 P -132 26

Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Multiple Minimum Solution with no Prime Implicants • G(A, B, C, D) = ∑m(0, 1, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15) • Minimum Solution F= C’D’ + B’D + BC B’C’ + BD’ + CD AB AC’ + AD 3 P -133 27

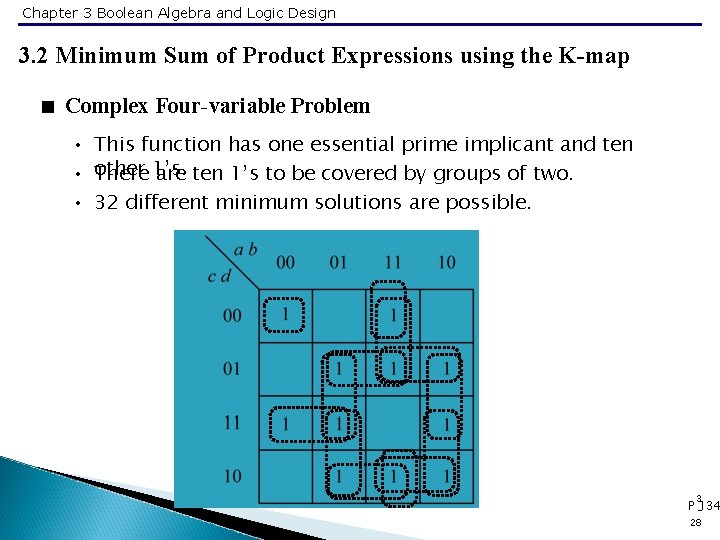
Chapter 3 Boolean Algebra and Logic Design 3. 2 Minimum Sum of Product Expressions using the K-map < Complex Four-variable Problem • • • This function has one essential prime implicant and ten other There 1’s. are ten 1’s to be covered by groups of two. 32 different minimum solutions are possible. 3 P -134 28

Chapter 3 Boolean Algebra and Logic Design 3. 3 Don’t Cares < Prime Implicant • Rectangle of 1, 2, 4, 8 … 1’s or X’s not included in any one larger rectangle. • X’s (don’t cares) are treated as 1’s < Essential Prime Implicant • Prime implicant covers at least one 1 not covered by any other prime implicant. • Don’t cares (X’s) do not make a prime implicant essential. 3 29

Chapter 3 Boolean Algebra and Logic Design 3. 3 Don’t Cares < Minimum solution with Don’t cares(1) • F(A, B, C, D) = ∑m(1, 7, 10, 11, 13) + ∑d(5, 8, 15) • Minimum Solution F = BC + A’C’D + AB’C F = BC + A’C’D + (AB’D’ or ACD) are not used in the minimum solution 3 P -135 30

Chapter 3 Boolean Algebra and Logic Design 3. 3 Don’t Cares < Minimum solution with Don’t cares(2) • g(w, x, y, z) = ∑m(4, 7, 9, 10, 12, 13) + ∑d(0, 1, 2, 3) • Minimum Solution g 1 = x’z + w’y’z’ + wxy’ g 1 = x’z + w’yz + xy’z’ + wy’z 3 P -136 31

Chapter 3 Boolean Algebra and Logic Design 3. 3 Don’t Cares < Minimum solution with Don’t cares(3) • f(a, b, c, d) = ∑m(0, 2, 3, 4, 8, 10, 12, 13, 14, 15) + ∑d(7, 9) • Minimum Solution f 1 = c’d’ + ab + b’d’ + a’cd f 2 = c’d’ + ab + b’d’ + a’b’c f 3 = c’d’ + ab + ad’ + a’b’c 3 P -137 32

Chapter 3 Boolean Algebra and Logic Design 3. 3 Don’t Cares < Map Method 2 1. Find all essential prime implicants. 2. Replace all 1’s covered by the essential prime implicants with X’s. This highlights the 1’s that remain to be covered. 3. Then Choose enough of the other prime implicants(as in Method 1) 3 33

Chapter 3 Boolean Algebra and Logic Design 3. 3 Don’t Cares < Minimum solution with Don’t cares(4) • F(A, B, C, D) = ∑m(0, 3, 4, 5, 6, 7, 8, 10, 11, 14, 15) • Find the two essential prime implicants (A’B, CD) • Convert all of the 1’s covered to don’t cares. • Finally cover the remaining 1’s with AC and B’C’D’ • Minimum Solution F = A’B + CD + AC + B’C’D’ 3 P -138 34

Chapter 3 Boolean Algebra and Logic Design 3. 4 Product Of Sums(POS) < Finding a minimum POS expression 1. Map the complement of the function. (If there is already a map for the function, replace all 0’s by 1’s, all 1’s by 0’s and leave X’s unchanged. ) 2. Find the minimum SOP expression for the complement of the function (using the techniques of the previous two section). 3. Use De. Morgan’s theorem(P 11) to complement that expression, producing a POS expression. 3 35

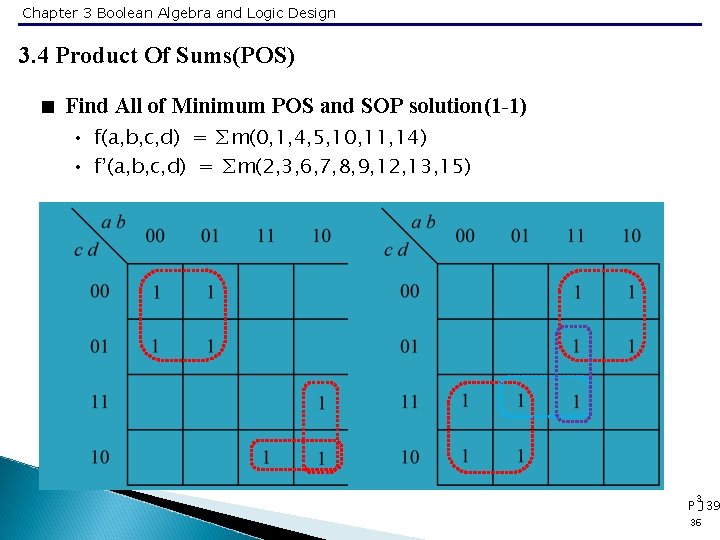
Chapter 3 Boolean Algebra and Logic Design 3. 4 Product Of Sums(POS) < Find All of Minimum POS and SOP solution(1 -1) • f(a, b, c, d) = ∑m(0, 1, 4, 5, 10, 11, 14) • f’(a, b, c, d) = ∑m(2, 3, 6, 7, 8, 9, 12, 13, 15) 3 P -139 36

Chapter 3 Boolean Algebra and Logic Design 3. 4 Product Of Sums(POS) < Find All of Minimum POS and SOP solution(1 -2) • Minimum Solution(SOP) • f = a’c’ + ab’c + acd • f’ = ac’ + a’c + abd • f’ = ac’ + a’c + bcd • Complement the solutions for f’s to get the minimum POS solutions for f • f = (a’+ c)(a + c’)(a’ + b’ + d’) • f = (a’+ c)(a + c’)(b’ + c’ + d’) 3 37

Chapter 3 Boolean Algebra and Logic Design 3. 4 Product Of Sums(POS) < Find All of Minimum POS and SOP solution(2 -1) • g(w, x, y, z) = ∑m(1, 3, 4, 6, 11) + ∑d(0, 8, 10, 12, 13) • Minimum Solution(SOP) w’x’y’ + x’yz • g = w’xz’ +w’x’z + x’yz w’x’z + wx’y 3 P -140 38

Chapter 3 Boolean Algebra and Logic Design 3. 4 Product Of Sums(POS) < Find All of Minimum POS and SOP solution(2 -2) • Minimum Solution(POS) wx • g’ = x’z’ + xz + wy’ + wz’ • Complement the solutions for g’s to get the minimum POS solutions for g (w + x) • g = (x’+ z’)(x + z)(w + y’) (w + z’) 3 P 140 -141 39

Chapter 3 Boolean Algebra and Logic Design 3. 5 Five-Variable Maps < A Five Variable Map • A five-variable map consists of 25 = 32 squares. 3 P -141 40

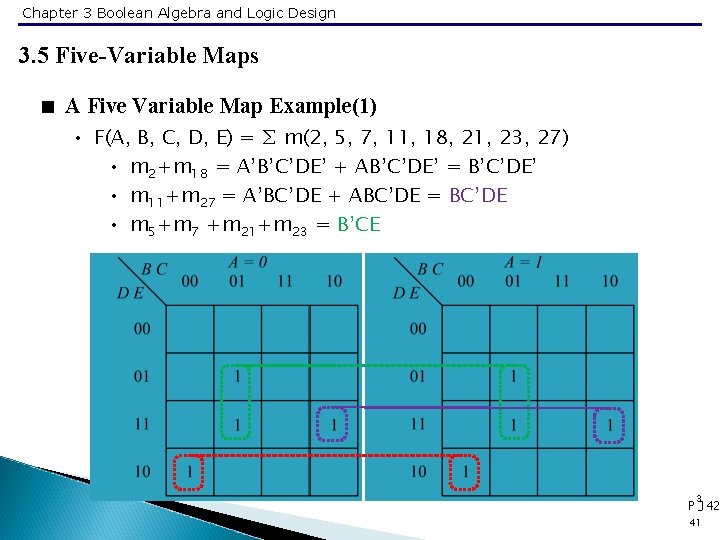
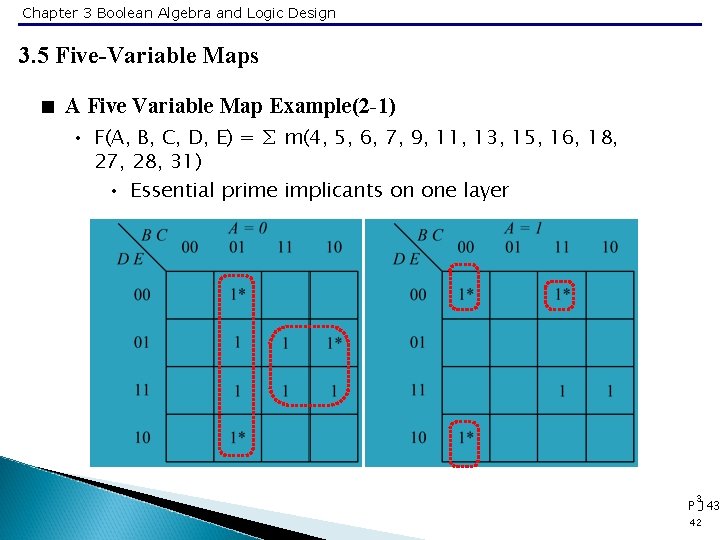
Chapter 3 Boolean Algebra and Logic Design 3. 5 Five-Variable Maps < A Five Variable Map Example(1) • F(A, B, C, D, E) = ∑ m(2, 5, 7, 11, 18, 21, 23, 27) • m 2+m 18 = A’B’C’DE’ + AB’C’DE’ = B’C’DE’ • m 11+m 27 = A’BC’DE + ABC’DE = BC’DE • m 5+m 7 +m 21+m 23 = B’CE 3 P -142 41

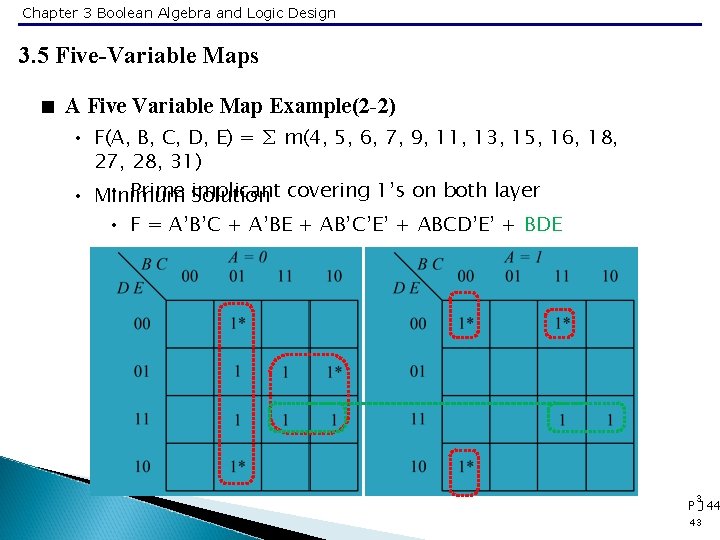
Chapter 3 Boolean Algebra and Logic Design 3. 5 Five-Variable Maps < A Five Variable Map Example(2 -1) • F(A, B, C, D, E) = ∑ m(4, 5, 6, 7, 9, 11, 13, 15, 16, 18, 27, 28, 31) • Essential prime implicants on one layer 3 P -143 42

Chapter 3 Boolean Algebra and Logic Design 3. 5 Five-Variable Maps < A Five Variable Map Example(2 -2) • F(A, B, C, D, E) = ∑ m(4, 5, 6, 7, 9, 11, 13, 15, 16, 18, 27, 28, 31) • Prime implicant • Minimum Solution covering 1’s on both layer • F = A’B’C + A’BE + AB’C’E’ + ABCD’E’ + BDE 3 P -144 43

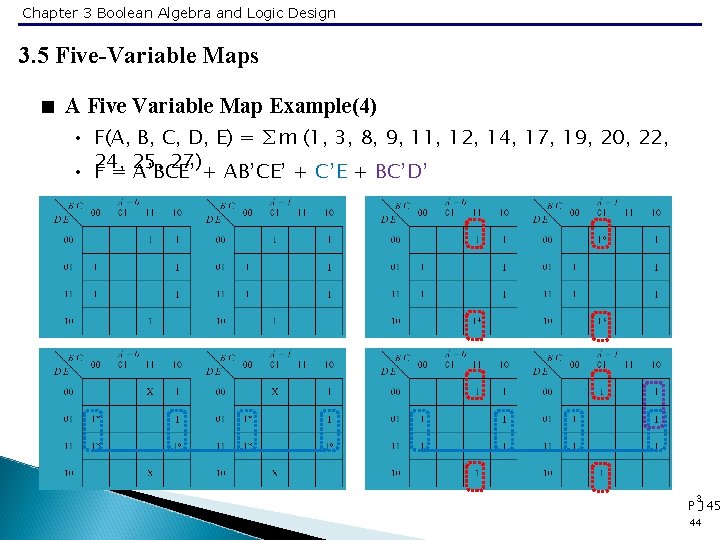
Chapter 3 Boolean Algebra and Logic Design 3. 5 Five-Variable Maps < A Five Variable Map Example(4) • F(A, B, C, D, E) = ∑m (1, 3, 8, 9, 11, 12, 14, 17, 19, 20, 22, 27)+ AB’CE’ + C’E + BC’D’ • 24, F = 25, A’BCE’ 3 P -145 44

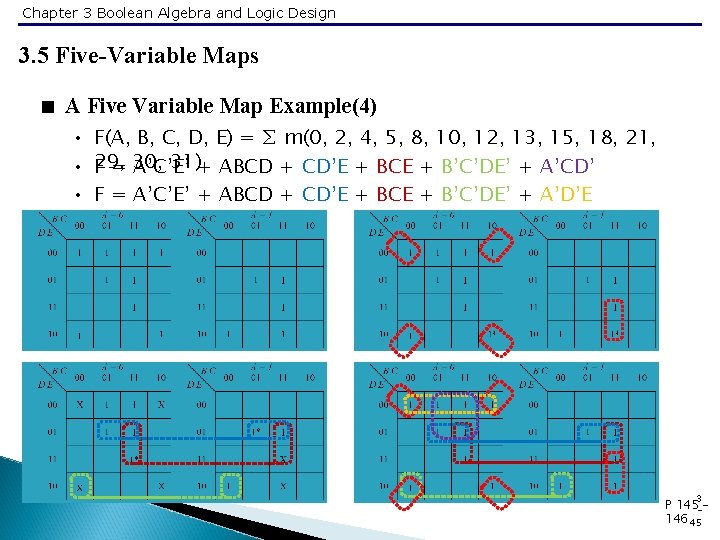
Chapter 3 Boolean Algebra and Logic Design 3. 5 Five-Variable Maps < A Five Variable Map Example(4) • • • F(A, B, C, D, E) = ∑ m(0, 2, 4, 5, 8, 10, 12, 13, 15, 18, 21, 29, 31)+ ABCD + CD’E + BCE + B’C’DE’ + A’CD’ F = 30, A’C’E’ F = A’C’E’ + ABCD + CD’E + BCE + B’C’DE’ + A’D’E 3 P 145 -146 45

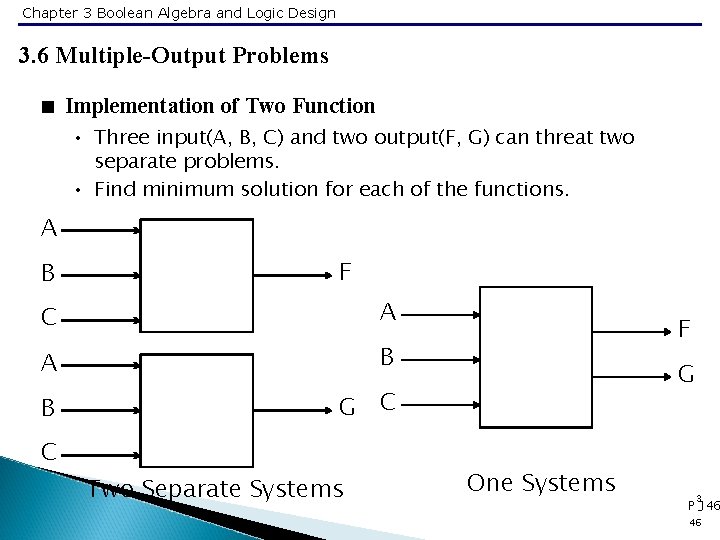
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Implementation of Two Function • Three input(A, B, C) and two output(F, G) can threat two separate problems. • Find minimum solution for each of the functions. A B F C A A B B G C C Two Separate Systems F G One Systems 3 P -146 46

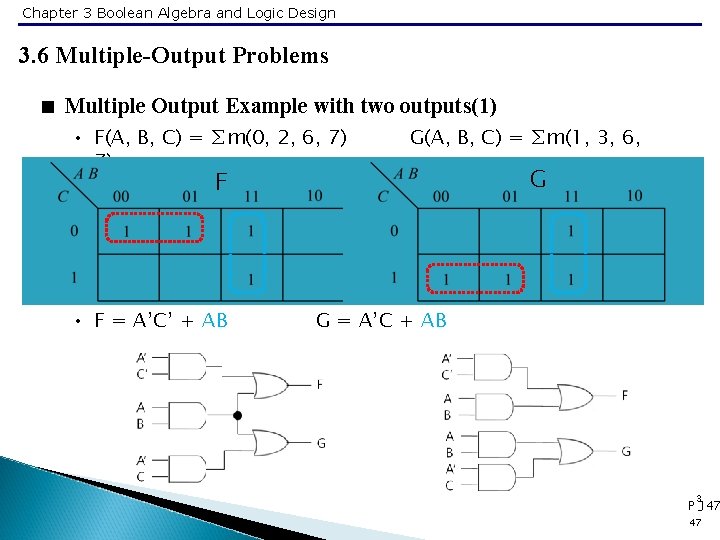
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs(1) • F(A, B, C) = ∑m(0, 2, 6, 7) 7) G(A, B, C) = ∑m(1, 3, 6, F • F = A’C’ + AB G G = A’C + AB 3 P -147 47

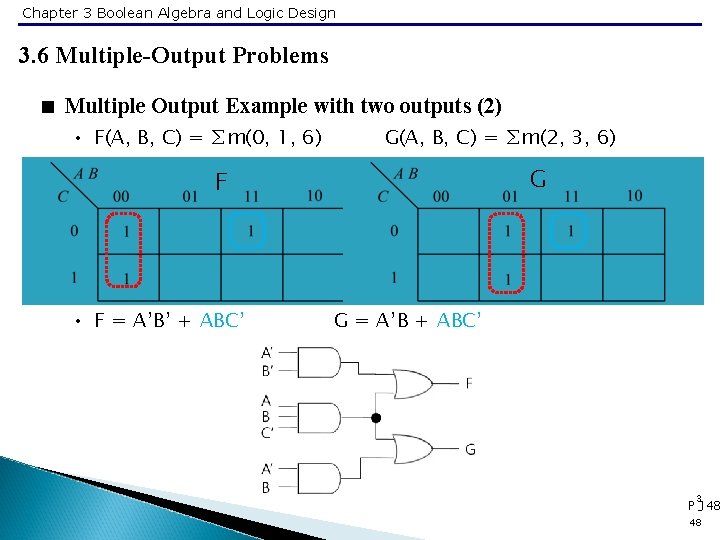
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (2) • F(A, B, C) = ∑m(0, 1, 6) G(A, B, C) = ∑m(2, 3, 6) G F • F = A’B’ + ABC’ G = A’B + ABC’ 3 P -148 48

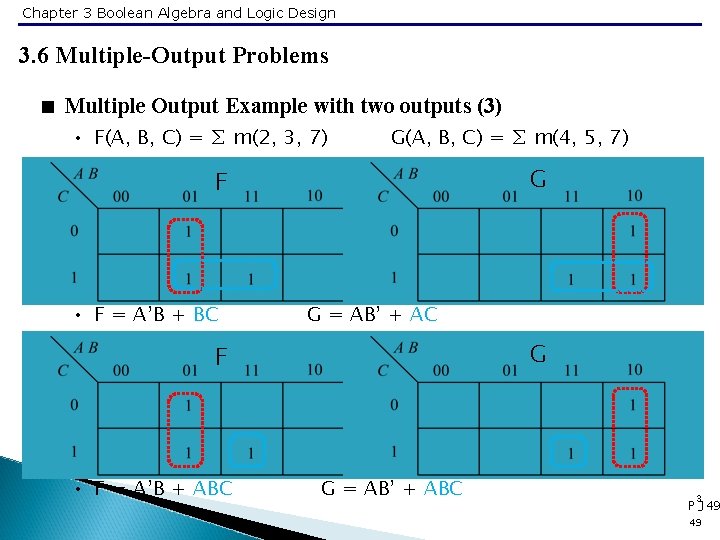
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (3) • F(A, B, C) = ∑ m(2, 3, 7) G(A, B, C) = ∑ m(4, 5, 7) G F • F = A’B + BC G = AB’ + AC G F • F = A’B + ABC G = AB’ + ABC 3 P -149 49

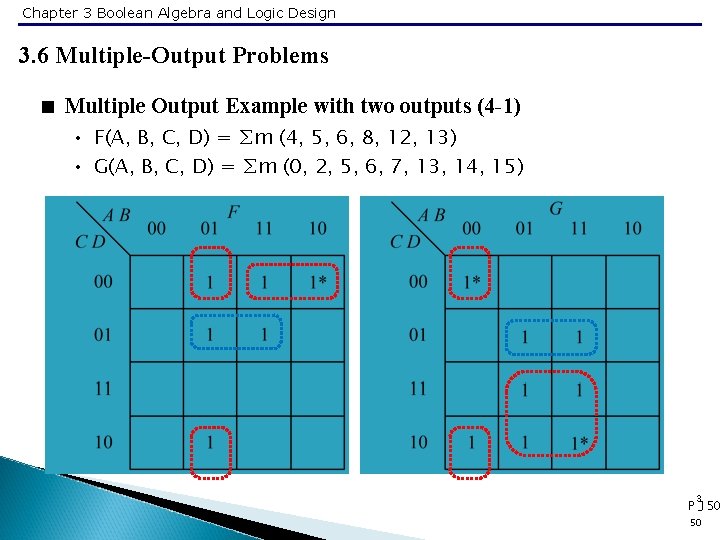
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (4 -1) • F(A, B, C, D) = ∑m (4, 5, 6, 8, 12, 13) • G(A, B, C, D) = ∑m (0, 2, 5, 6, 7, 13, 14, 15) 3 P -150 50

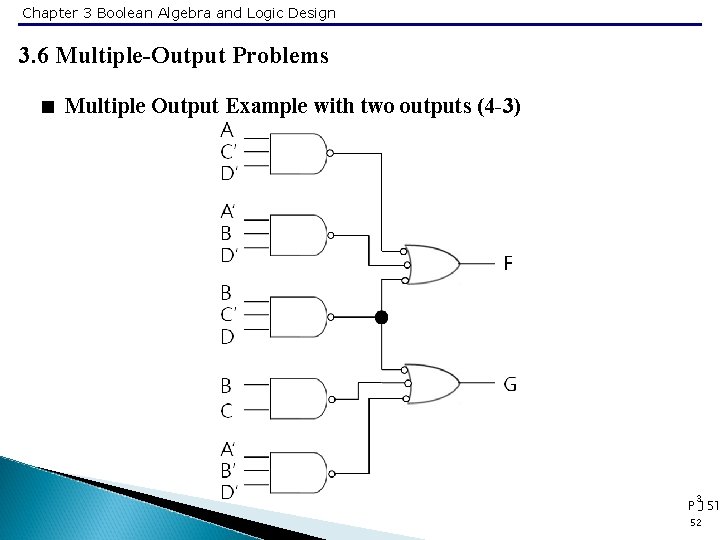
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (4 -2) • Solution 1 • F = AC’D’ + A’BD’ + BC’D • G = A’B’D’ + BC’D • 7 gates with 20 inputs • Solution 2 • F = AC’D’ + A’BD’ + BC’ • G = A’B’D + BC + BD • 8 gates with 21 inputs • The shared circuit costs less. 3 51

Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (4 -3) 3 P -151 52

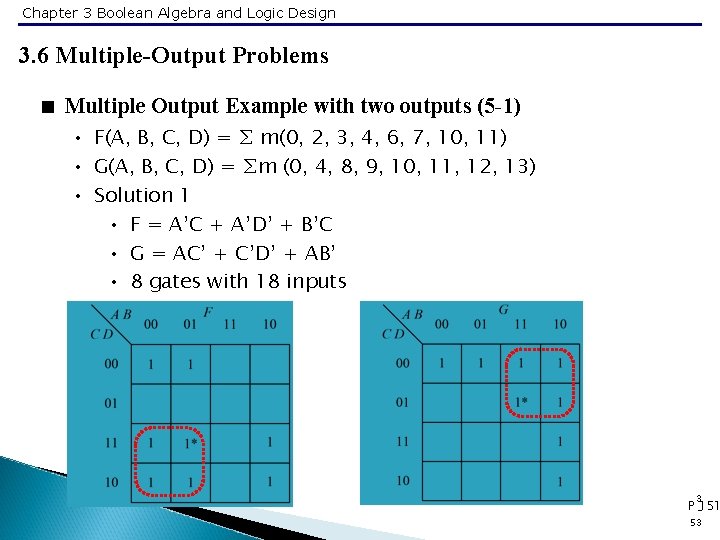
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (5 -1) • F(A, B, C, D) = ∑ m(0, 2, 3, 4, 6, 7, 10, 11) • G(A, B, C, D) = ∑m (0, 4, 8, 9, 10, 11, 12, 13) • Solution 1 • F = A’C + A’D’ + B’C • G = AC’ + C’D’ + AB’ • 8 gates with 18 inputs 3 P -151 53

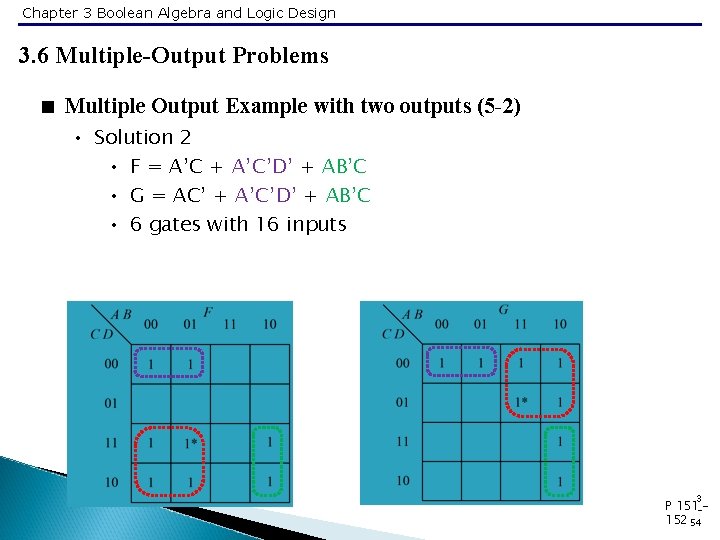
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with two outputs (5 -2) • Solution 2 • F = A’C + A’C’D’ + AB’C • G = AC’ + A’C’D’ + AB’C • 6 gates with 16 inputs 3 P 151 -152 54

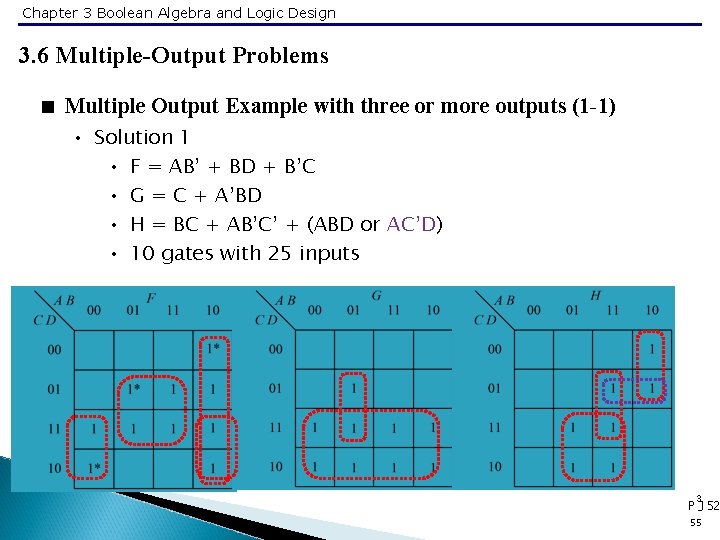
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with three or more outputs (1 -1) • Solution 1 • F = AB’ + BD + B’C • G = C + A’BD • H = BC + AB’C’ + (ABD or AC’D) • 10 gates with 25 inputs 3 P -152 55

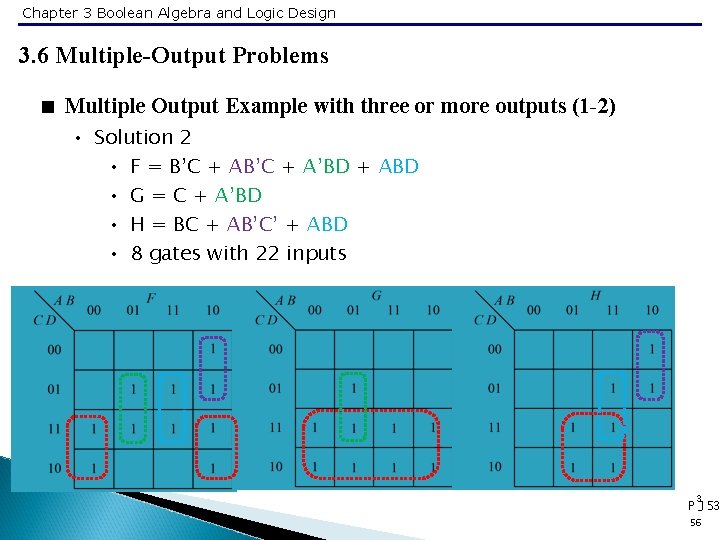
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with three or more outputs (1 -2) • Solution 2 • F = B’C + A’BD + ABD • G = C + A’BD • H = BC + AB’C’ + ABD • 8 gates with 22 inputs 3 P -153 56

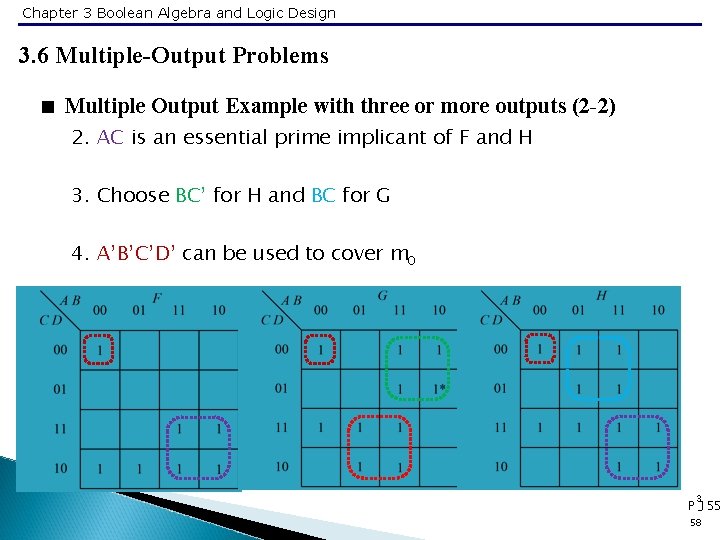
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with three or more outputs (2 -1) • F(A, B, C, D) = ∑ m(0, 2, 6, 10, 11, 14, 15) • G(A, B, C, D) = ∑ m(0, 3, 6, 7, 8, 9, 12, 13, 14, 15) • H(A, B, C, D) = ∑ m(0, 3, 4, 5, 7, 10, 11, 12, 13, 14, 15) 1. The only 1 that cannot be shared and makes a prime implicant essential is m 9 3 P 153 -154 57

Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with three or more outputs (2 -2) 2. AC is an essential prime implicant of F and H 3. Choose BC’ for H and BC for G 4. A’B’C’D’ can be used to cover m 0 3 P -155 58

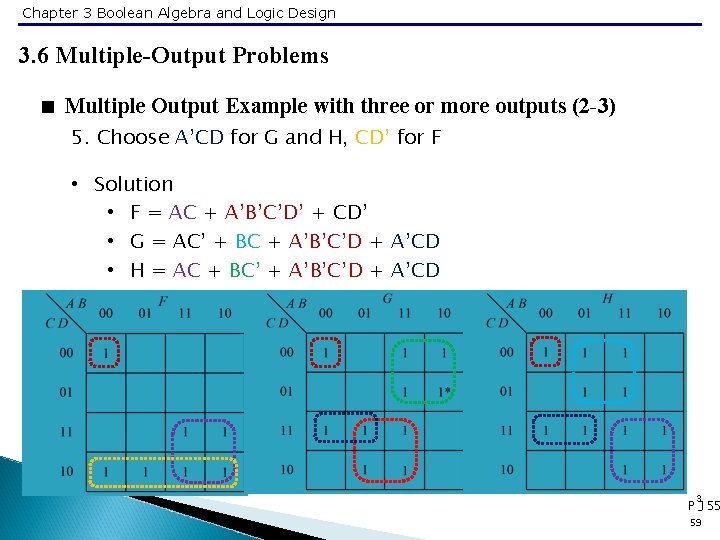
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with three or more outputs (2 -3) 5. Choose A’CD for G and H, CD’ for F • Solution • F = AC + A’B’C’D’ + CD’ • G = AC’ + BC + A’B’C’D + A’CD • H = AC + BC’ + A’B’C’D + A’CD 3 P -155 59

Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with Don’t cares(1 -1) • F(A, B, C, D) = ∑ m(2, 3, 4, 6, 9, 11, 12) + ∑ d(0, 1, 14, 15) • G(A, B, C, D) = ∑ m(2, 6, 10, 11, 12) + ∑d(0, 1, 14, 15) 1. The only prime implicant made essential by a 1 that is not shared circled, B’D 2. m 11 has been covered in F. We must use AC in G to cover m 11. ABD’ is used for G and F which can be shared. 3 P -155 60

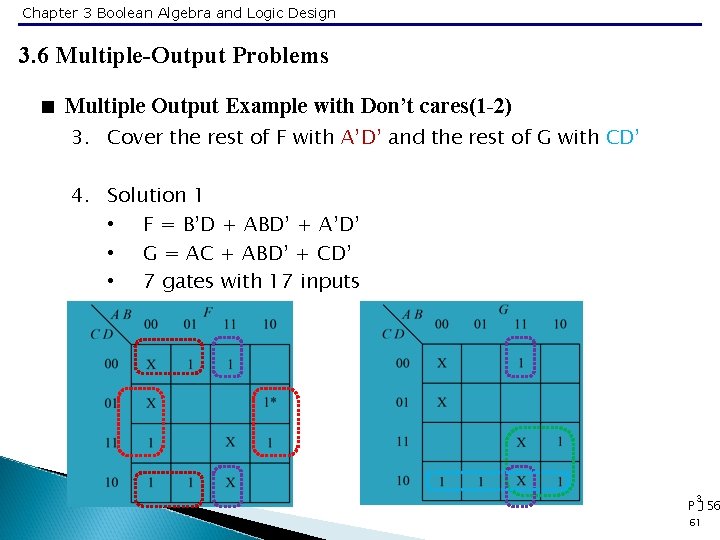
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with Don’t cares(1 -2) 3. Cover the rest of F with A’D’ and the rest of G with CD’ 4. Solution 1 • F = B’D + ABD’ + A’D’ • G = AC + ABD’ + CD’ • 7 gates with 17 inputs 3 P -156 61

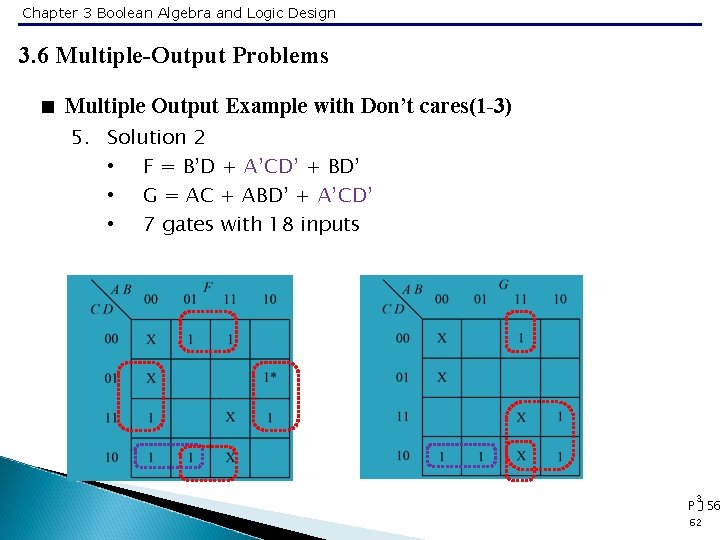
Chapter 3 Boolean Algebra and Logic Design 3. 6 Multiple-Output Problems < Multiple Output Example with Don’t cares(1 -3) 5. Solution 2 • F = B’D + A’CD’ + BD’ • G = AC + ABD’ + A’CD’ • 7 gates with 18 inputs 3 P -156 62