Chapter 3 Symmetries Symmetry is very important in

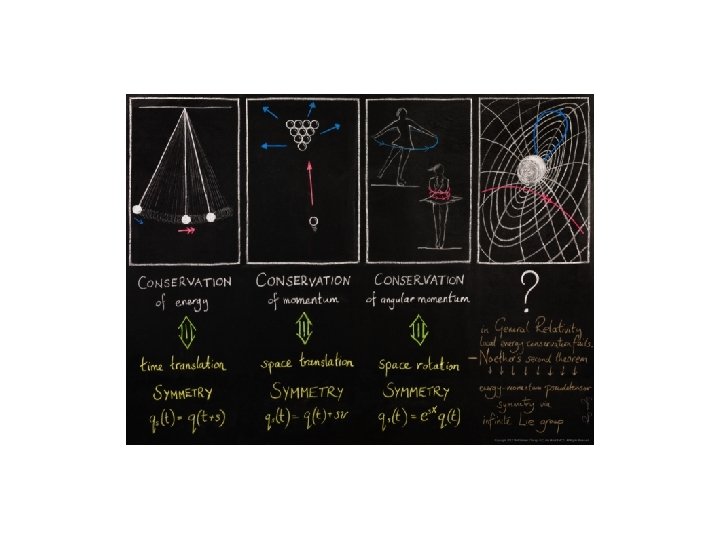
Chapter 3: Symmetries Symmetry is very important in physics and especially particle physics. Symmetries are connected to conservation laws (rotational invariance angular momentum conservation; translational invariance momentum conservation) Transformations can be continuous or discrete e. g. translations, rotations, Lorentz transformations are continuous Spatial reflection through the origin (parity) is discrete.

Emmy Noether, 1882 -1935

Associated conservation laws are additive (cont symmetries) Associated conservation laws are multiplicative (discrete symmetries) Two types of symmetry breaking: Explicit breaking (when the interactions do not respect the symmetry. The corresponding quantum numbers are not conserved in the interaction. ) Spontaneous breaking (when the interaction does respect the symmetry; mathematically the Lagrangian is invariant under the corresponding group but its states are not).

Next example: Parity or mirror reflection is a discrete transformation

Question: What does the parity do to the following quantities Spatial position r Time t Momenta p Angular momentum r x p Intrinsic spin

Parity of hydrogenic wave functions Let’s focus on the angular part

The overall angular wave function Y_lm is the product of these two pieces. Question: What is the parity of the hydrogenic wave functions ? Answer: Parity = (-1)l ; we will use this result in the future.

Parity is a multiplicative quantum number. Parity is found to be conserved in electromagnetic and strong interactions. Question: What about the weak interaction ? Elementary particles have intrinsic parity

Is this a strong, weak or electromagnetic interaction ? What is the product of intrinsic parities in the initial and final states ? Ans: +1 and -1. How can parity be conserved ? Ans: orbital angular momentum between a pair of particles in the final state.