Chapter 3 Student Notes Chapter 3 Test Friday

Chapter 3 Student Notes Chapter 3 Test Friday, October 12 th

3. 1 Parallel Lines and Transversals

Parallel Lines A C B D

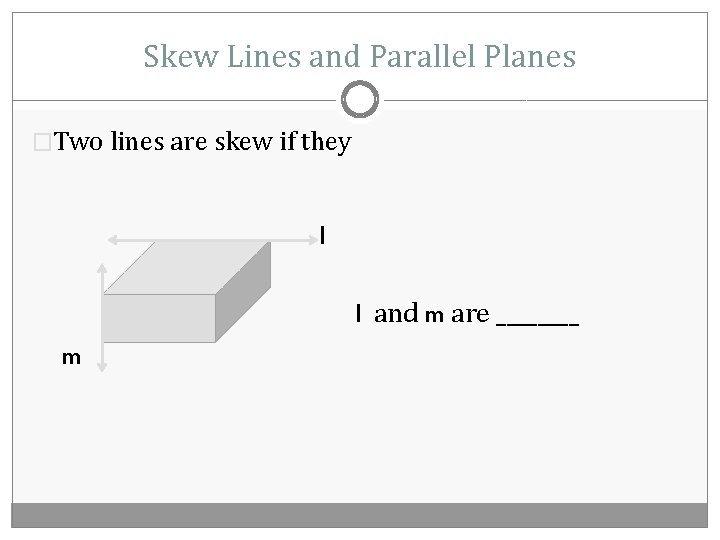
Skew Lines and Parallel Planes �Two lines are skew if they l l and m are ____ m

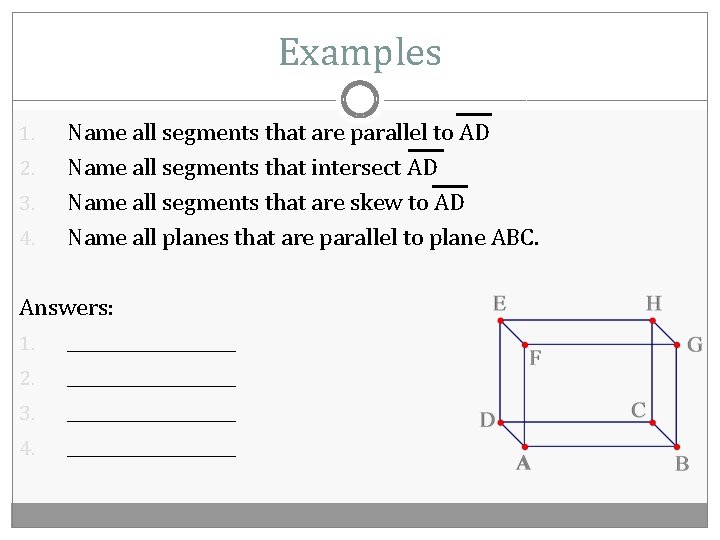
Examples 1. 2. 3. 4. Name all segments that are parallel to AD Name all segments that intersect AD Name all segments that are skew to AD Name all planes that are parallel to plane ABC. Answers: 1. __________ 2. __________ 3. __________ 4. __________

Transversal – ______________ Exterior Angles – ___________ Interior Angles – ___________ 1 3 4 l m 2 5 7 t 6 8

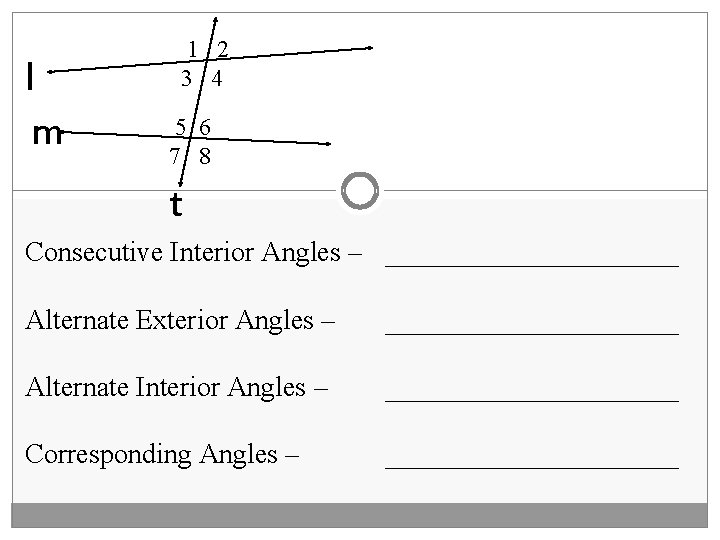
l m 1 2 3 4 5 6 7 8 t Consecutive Interior Angles – ___________ Alternate Exterior Angles – ___________ Alternate Interior Angles – ___________ Corresponding Angles – ___________

q p 1 2 3 4 8 7 6 5 9 10 11 12 16 17 18 19 r s Transversal 1. 2. 3. 4. 5. 3 & 11 11 & 17 17 & 1 2 & 3 4 & 6 Name the transversal that forms each pair of angles. Then name the special name for each pair. ____ ____ Special Angle Pair Name __________________ _________

3 -2 Angles and Parallel Lines

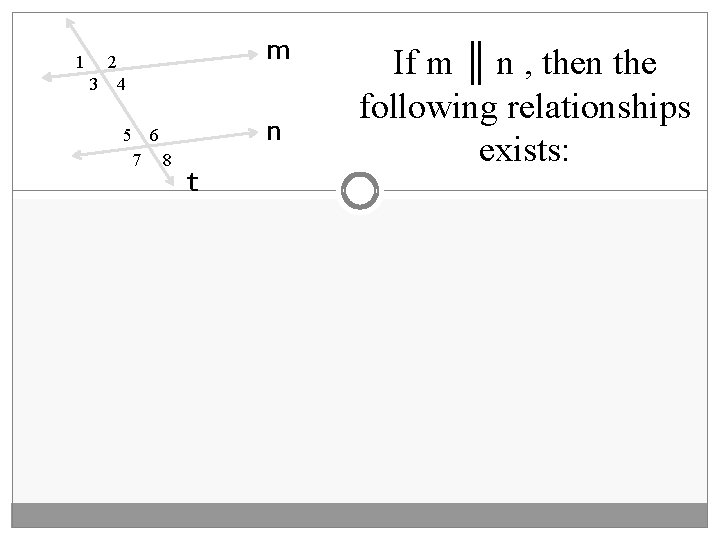
1 m 2 3 4 5 6 7 8 n t If m ║ n , then the following relationships exists:

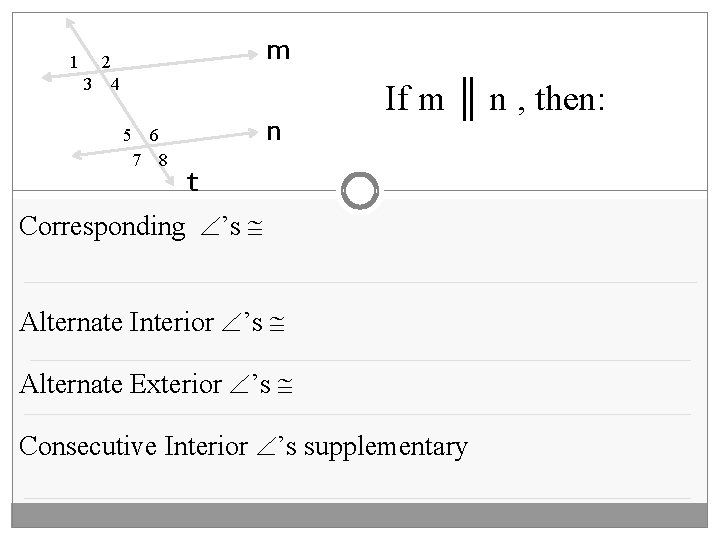
1 m 2 3 4 5 6 7 8 n If m ║ n , then: t Corresponding ’s Alternate Interior ’s Alternate Exterior ’s Consecutive Interior ’s supplementary

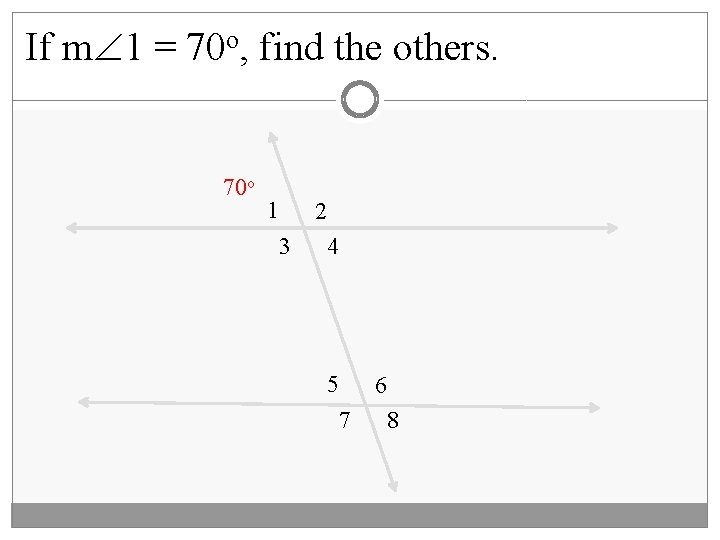
If m 1 = 70 o, find the others. 70 o 1 2 3 4 5 6 7 8

More Examples If line AB is parallel to line CD and s is parallel to t, find: 1. The value of x, if m 3 = 4 x + 6 and m 11 = 126. 2. The value of x, if m 1 = 100 and m 8 = 2 x + 10. 3. The value of y, if m 11 = 3 y – 5 and m 16 = 2 y + 20.

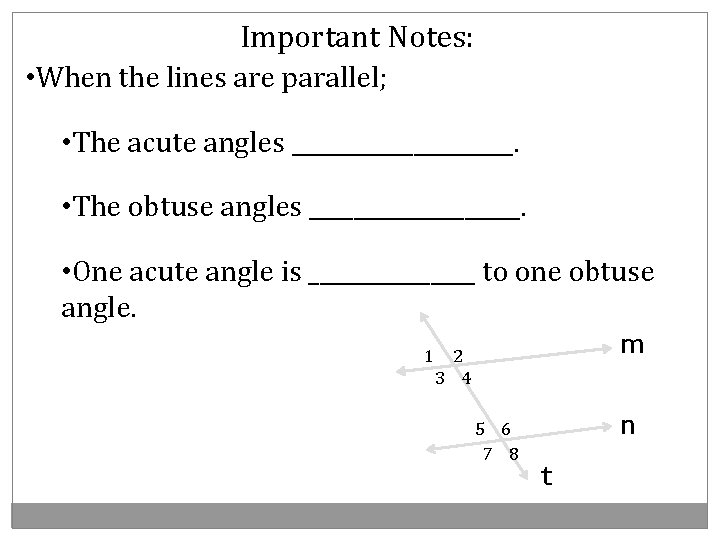
Important Notes: • When the lines are parallel; • The acute angles __________. • The obtuse angles __________. • One acute angle is ________ to one obtuse angle. 1 m 2 3 4 5 6 7 8 n t

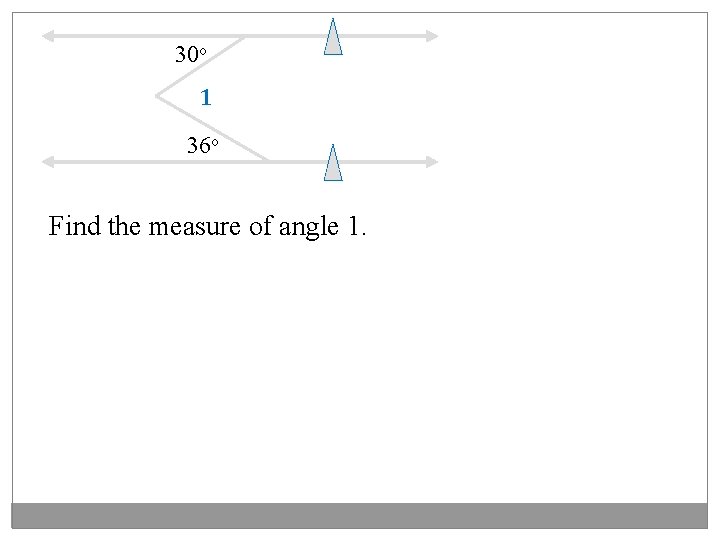
30 o 1 36 o Find the measure of angle 1.

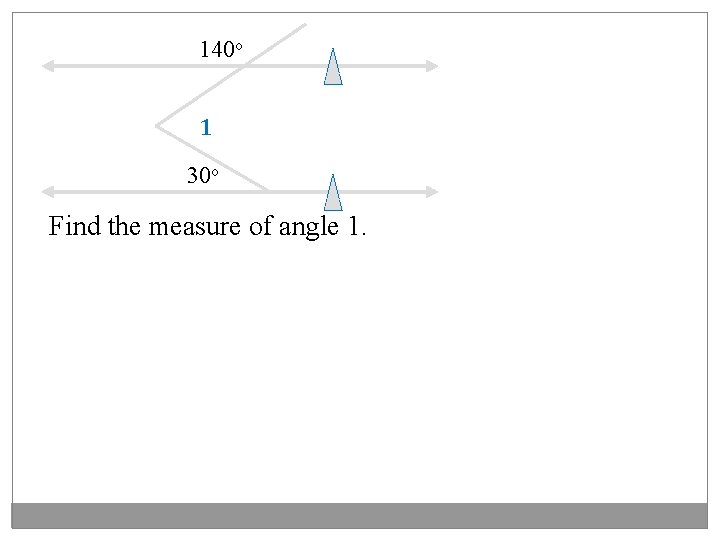
140 o 1 30 o Find the measure of angle 1.

Find the value of x and y. (5 y + (5 x)o 10) o (10 y + 5) o

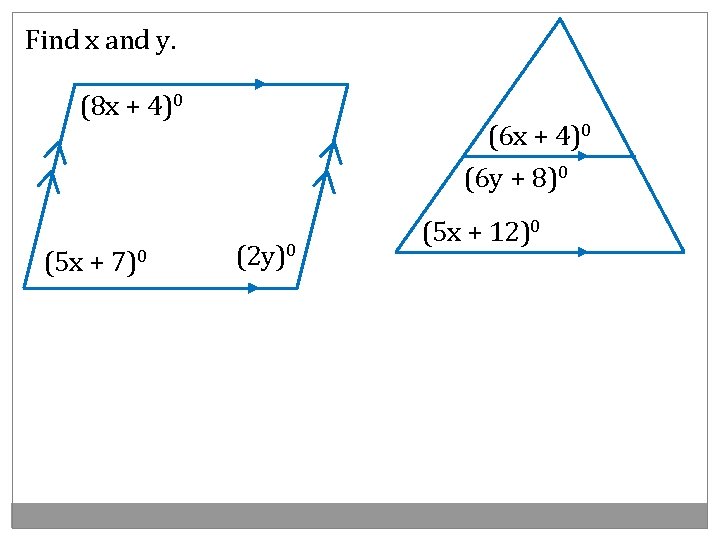
Find x and y. (8 x + 4)0 (6 y + 8)0 (5 x + 7)0 (2 y)0 (5 x + 12)0

3 -3 Slopes of Lines

Slope of ǁ, and⊥ lines

Determine if each pair of lines are ǁ , ⊥, or neither. 1. Line 1, m = -2 Line 2, m = ½ 2. Line 3, m = 3 Line 4, m = 3 3. Line 5, m = 4/3 Line 6, m = 3/4 4. Line 7, m = -1 Line 8, m = 1

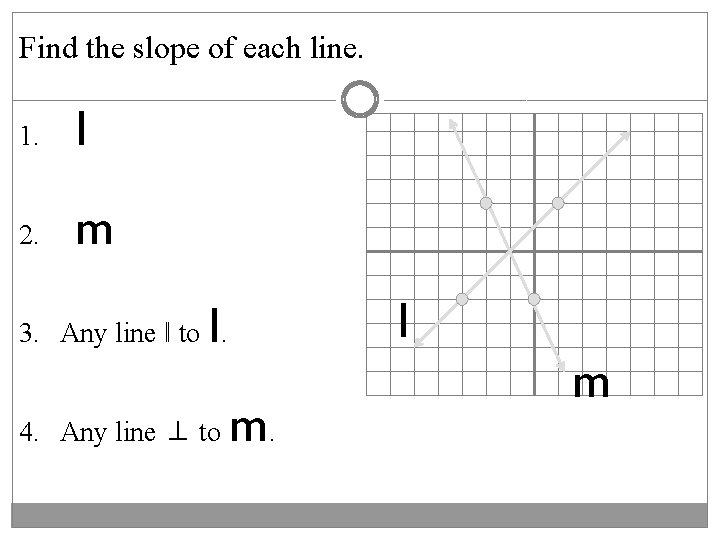
Find the slope of each line. 1. l 2. m l 3. Any line ǁ to. 4. Any line ⊥ to m. l m

Slope of a Line �The slope of the non-vertical line through the points and is m= The slope of a vertical line ______. The slope of a horizontal line is _______.

Examples Find the slope of the line through the given points. (-4, 7) and (3, 7)

Examples Find the slope of the line through the given points. (3, -1) and (3, 2)

Examples Find the slope of the line through the given points. (1, -4) and (2, 5)

Examples Find the slope of the line through the given points. (-2, 5) and (1, -1)

Given each pair of points, Determine if AB ǁ CD, AB ⊥ CD, or neither. 1. A(-3, -2) B(9, 1) C(3, 6) D(5, -2) 2. A(5, -4) B(10, 0) C(9, -8) D(5, -13)

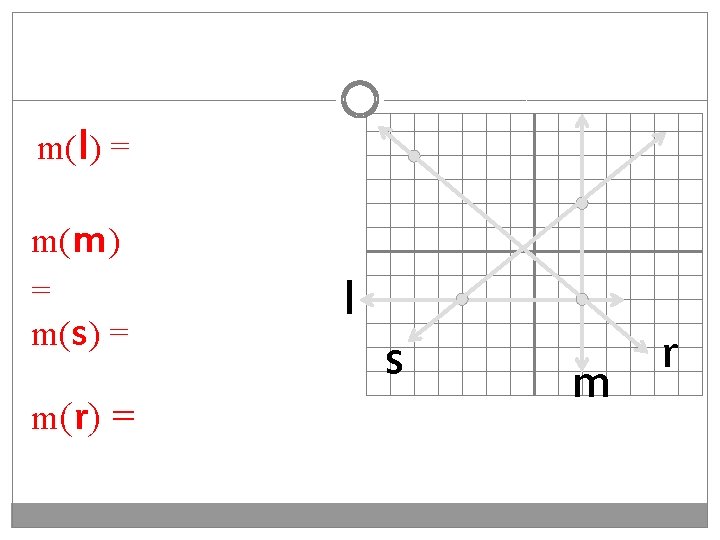
m(l) = m(m) = m(s) = m (r ) = l s m r

Graph each line described below. 1. m = 3, passes through (2, 1) 2. Passes through (-4, -5) the line that passes through MN, M(-1, -3), N(-3, 4) m(MN) = m( ) =

3 -5 Proving Lines Parallel

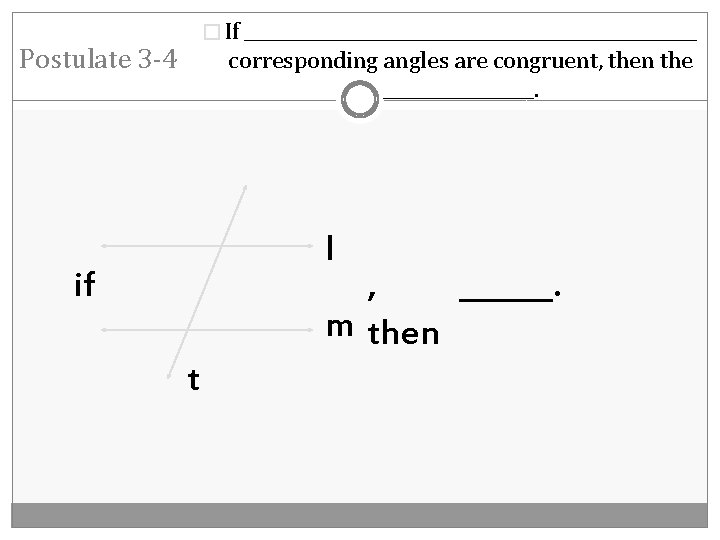
� If __________________________ Postulate 3 -4 corresponding angles are congruent, then the _________. l if , ______. m then t

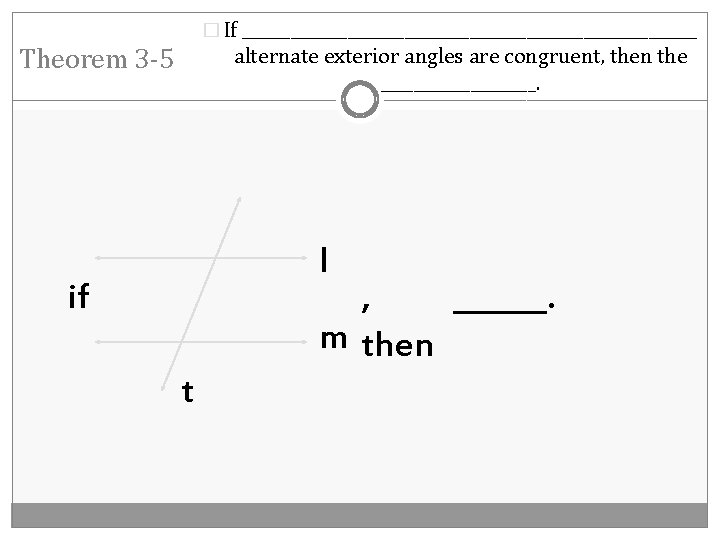
� If ____________________________ Theorem 3 -5 alternate exterior angles are congruent, then the __________. l if , ______. m then t

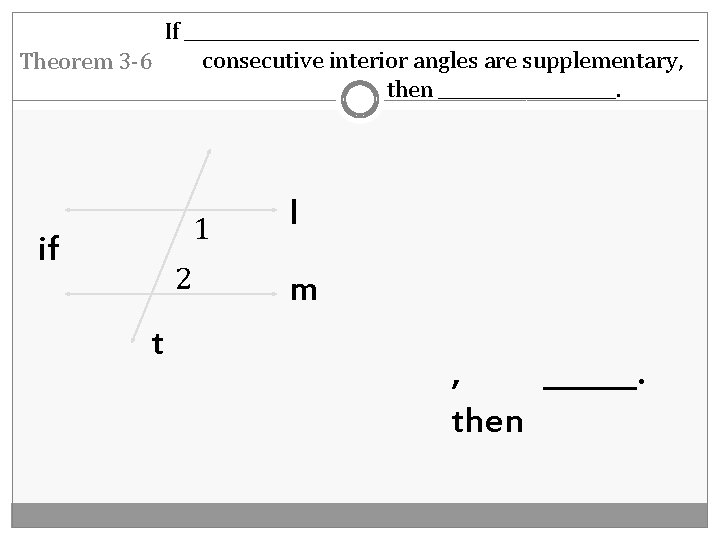
If _____________________________ consecutive interior angles are supplementary, Theorem 3 -6 then __________. 1 if 2 t l m , ______. then

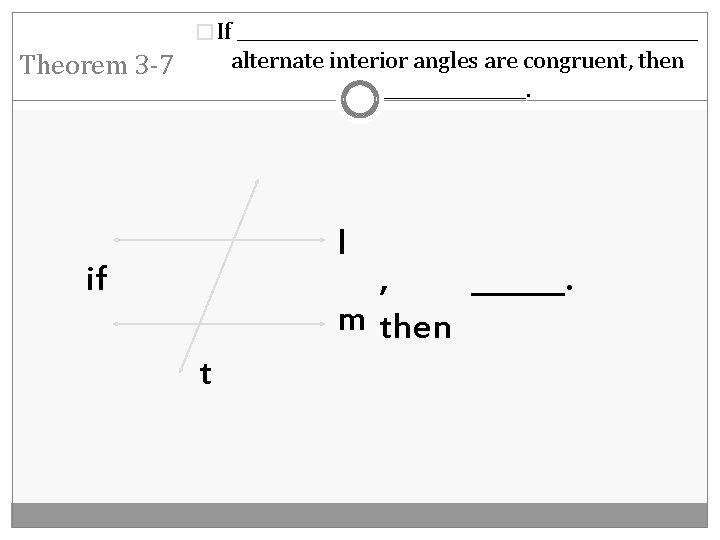
� If __________________________ alternate interior angles are congruent, then ________. Theorem 3 -7 l , ______. m then if t

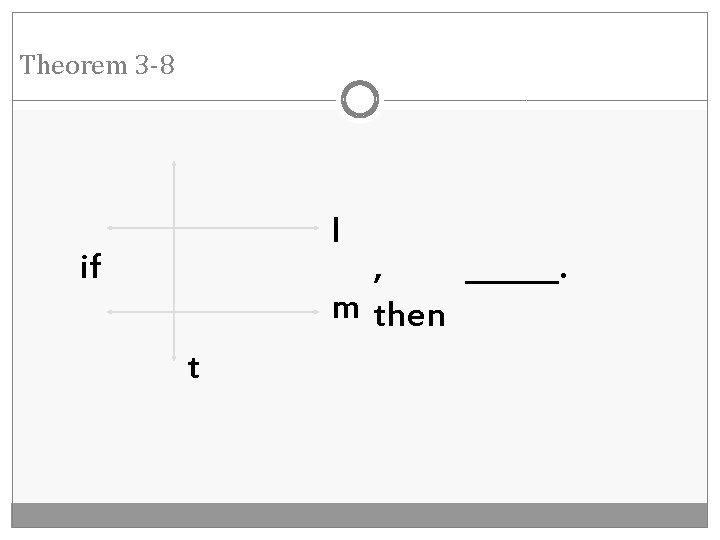
Theorem 3 -8 l , ______. m then if t

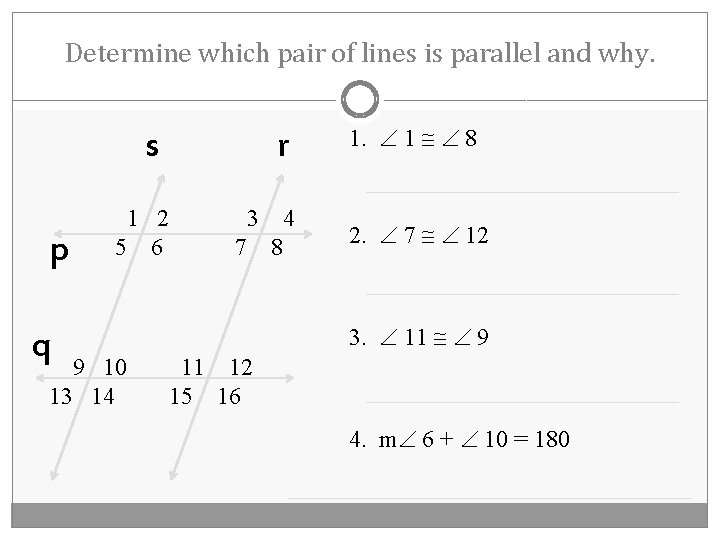
Determine which pair of lines is parallel and why. s p q 1 2 5 6 r 9 10 13 14 3 7 4 8 1. 1 8 2. 7 12 3. 11 9 11 12 15 16 4. m 6 + 10 = 180

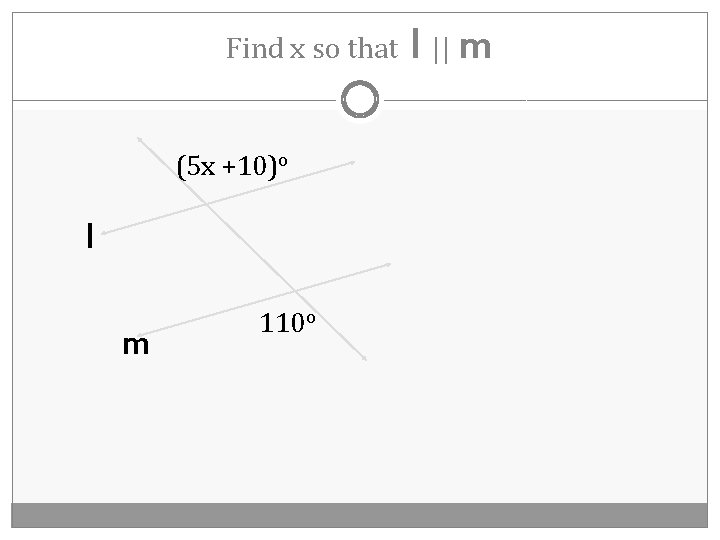
Find x so that (5 x +10)o l m 110 o l || m

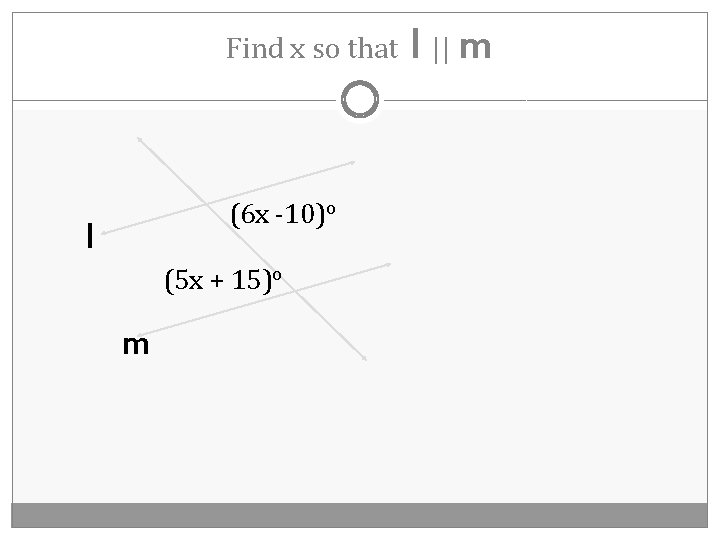
Find x so that (6 x -10)o l (5 x + 15)o m l || m

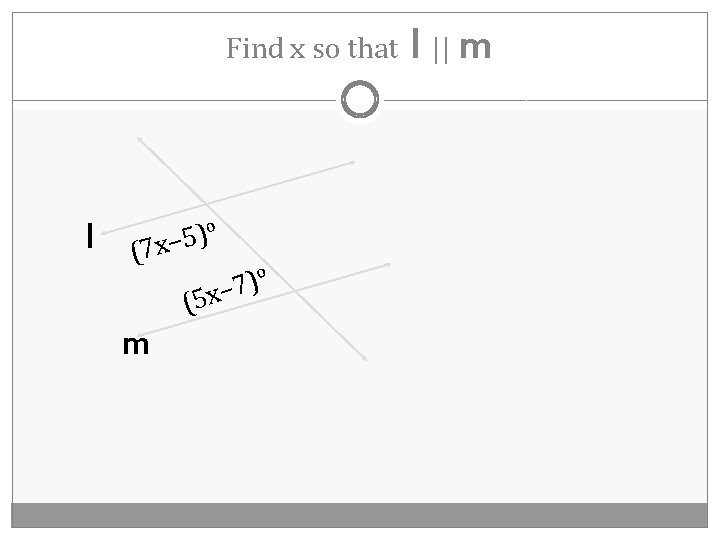
Find x so that l o ) 5 – x (7 (5 o ) x– 7 m l || m

Find x so that l m (7 x– 1)o l || m

3. 6 Perpendiculars and Distance

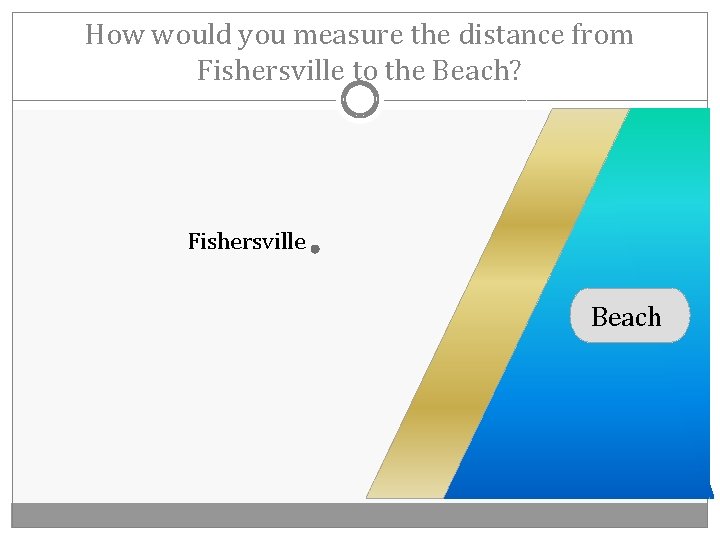
How would you measure the distance from Fishersville to the Beach? Fishersville Beach

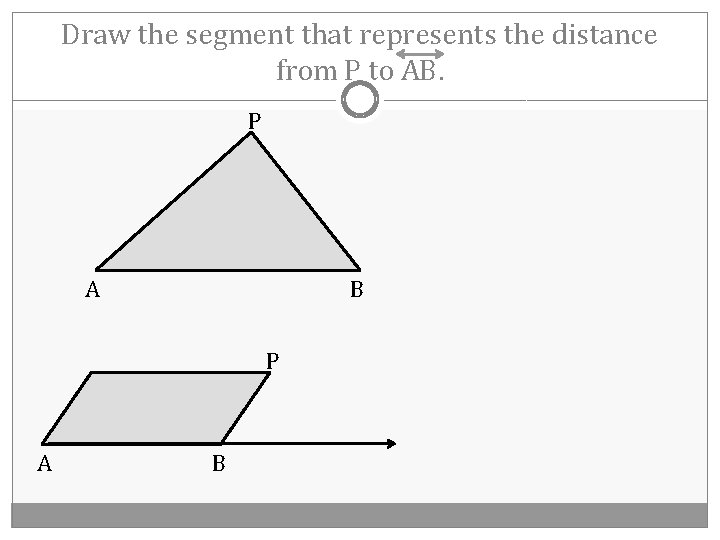
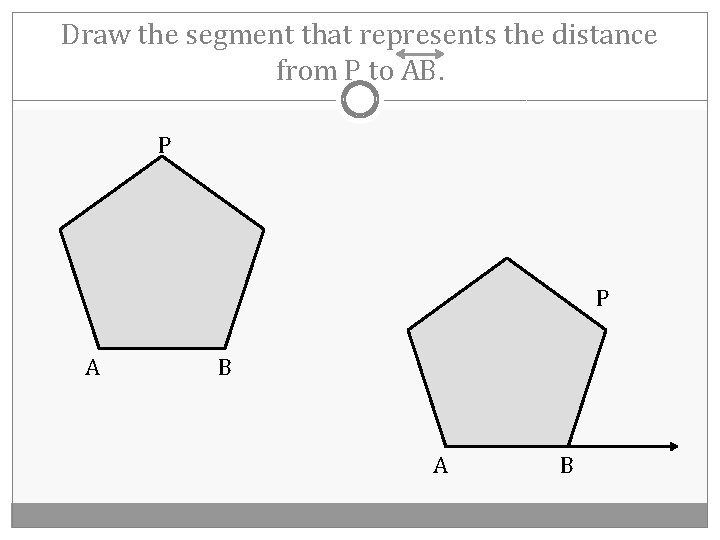
Draw the segment that represents the distance from P to AB. P A B

Draw the segment that represents the distance from P to AB. P P A B

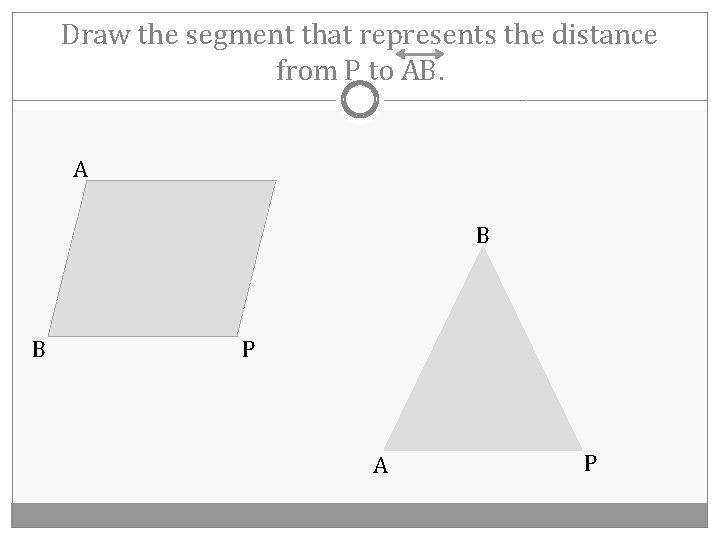
Draw the segment that represents the distance from P to AB. A B B P A P