Chapter 3 Stress and Equilibrium Body and Surface

Chapter 3 Stress and Equilibrium Body and Surface Forces Body Forces: F(x) Surface Forces: T(x) (a) Cantilever Beam Under Self-Weight Loading S (b) Sectioned Axially Loaded Beam Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

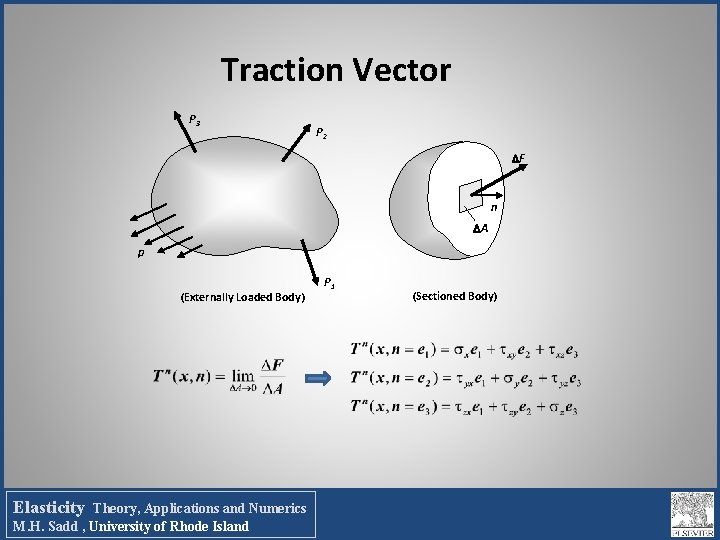
Traction Vector P 3 P 2 F n A p (Externally Loaded Body) Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island P 1 (Sectioned Body)

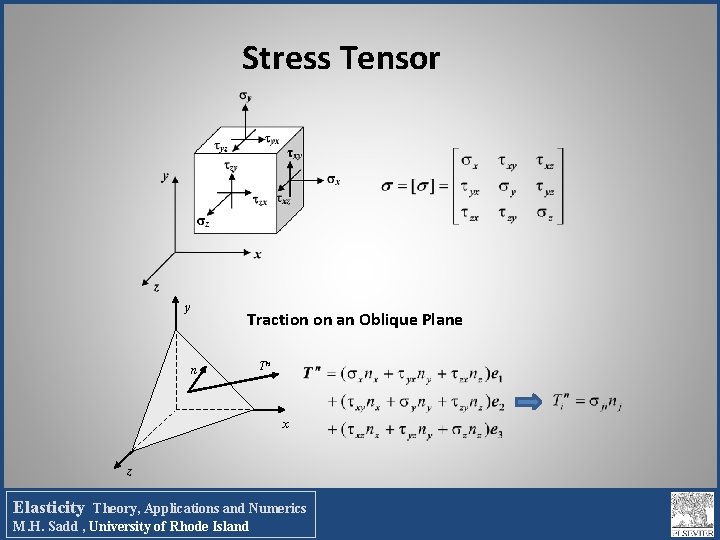
Stress Tensor y n Traction on an Oblique Plane Tn x z Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

Stress Transformation Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

Two-Dimensional Stress Transformation Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

Principal Stresses & Directions (General Coordinate System) Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island (Principal Coordinate System)

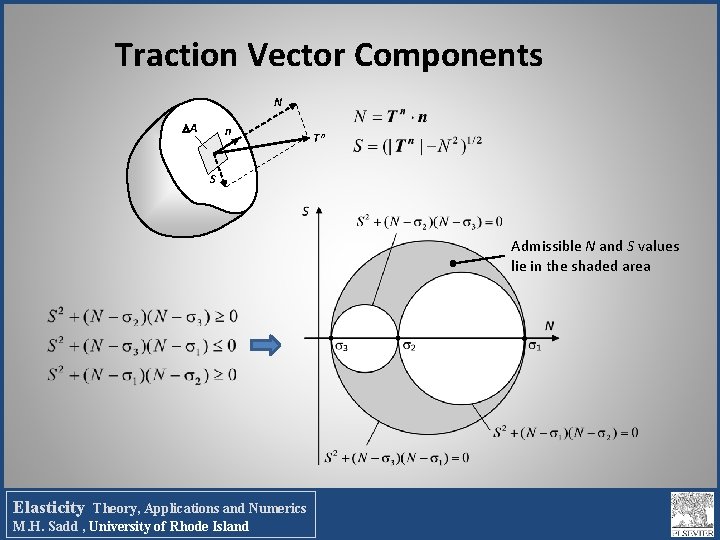
Traction Vector Components N A n Tn S Admissible N and S values lie in the shaded area Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island Mohr’s Circles of Stress

Example 3 -1 Stress Transformation Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

Spherical, Deviatoric, Octahedral and von Mises Stresses. . . Spherical Stress Tensor. . . Deviatoric Stress Tensor. . . Octahedral Normal and Shear Stresses . . . von Mises Stress Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

Stress Distribution Visualization Using 2 -D or 3 -D Plots of Particular Contour Lines Particular Stress Components Principal Stress Components Maximum Shear Stress von Mises Stress Isochromatics (lines of principal stress difference = constant; same as max shear stress) • Isoclinics (lines along which principal stresses have constant orientation) • Isopachic lines (sum of principal stresses = constant) • Isostatic lines (tangent oriented along a particular principal stress; sometimes called stress trajectories) • • • Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

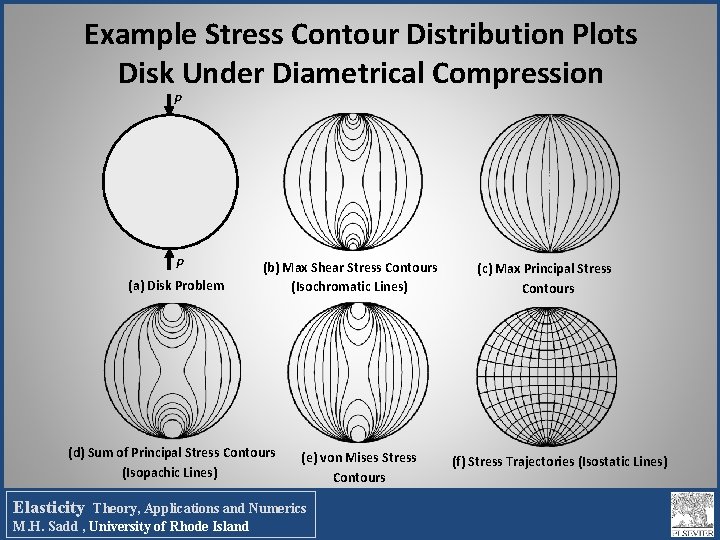
Example Stress Contour Distribution Plots Disk Under Diametrical Compression P P (a) Disk Problem (b) Max Shear Stress Contours (Isochromatic Lines) (d) Sum of Principal Stress Contours (Isopachic Lines) Elasticity (e) von Mises Stress Contours Theory, Applications and Numerics M. H. Sadd , University of Rhode Island (c) Max Principal Stress Contours (f) Stress Trajectories (Isostatic Lines)

Equilibrium Equations Tn S F Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island V

Stress & Traction Components in Cylindrical Coordinates x 3 z z z x 1 r rz x 2 d dr Equilibrium Equations Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island

Stress & Traction Components in Spherical Coordinates x 3 R R x 2 x 1 Equilibrium Equations Elasticity Theory, Applications and Numerics M. H. Sadd , University of Rhode Island