Chapter 3 Stoichiometry 3 1 MoleMass Relationships in

Chapter 3 Stoichiometry 3 -1

Mole-Mass Relationships in Chemical Systems 3. 1 The Mole 3. 2 Determining the Formula of an Unknown Compound 3. 3 Writing and Balancing Chemical Equations 3. 4 Calculating the Amounts of Reactant and Product 3. 5 Fundamentals of Solution Stoichiometry 3 -2

Definition of the Mole mole - the amount of a substance that contains the same number of particles as there atoms in exactly 12 g of carbon-12. This amount contains 6. 022 x 1023 particles. The number, 6. 022 x 1023, is called Avogadro’s number and is abbreviated N. One mole (1 mol) contains 6. 022 x 1023 particles (to four significant figures) 3 -3

Counting Objects of Fixed Relative Mass Figure 3. 1 12 red marbles at 7 g each = 84 g 12 yellow marbles at 4 g each = 48 g 3 -4 55. 85 g Fe = 6. 022 x 1023 atoms Fe 32. 07 g S = 6. 022 x 1023 atoms S

One Mole of Common Substances Ca. CO 3 100. 09 g Figure 3. 2 3 -5 Oxygen 32. 00 g Water 18. 02 g Copper 63. 55 g

Table 3. 1 Summary of Mass Terminology Term Definition Unit isotopic mass of an isotope of an element amu atomic mass (also called atomic weight) average of the masses of the naturally occurring isotopes of an element weighted according to their abundance amu molecular sum of the atomic masses of the atoms (or ions) in a molecule (or formula unit) (or formula) mass (also called molecular weight) amu mass of 1 mole of chemical particles molar mass (M) (atoms, ions, molecules, formula units) (also called gram-molecular weight) g/mol 3 -6

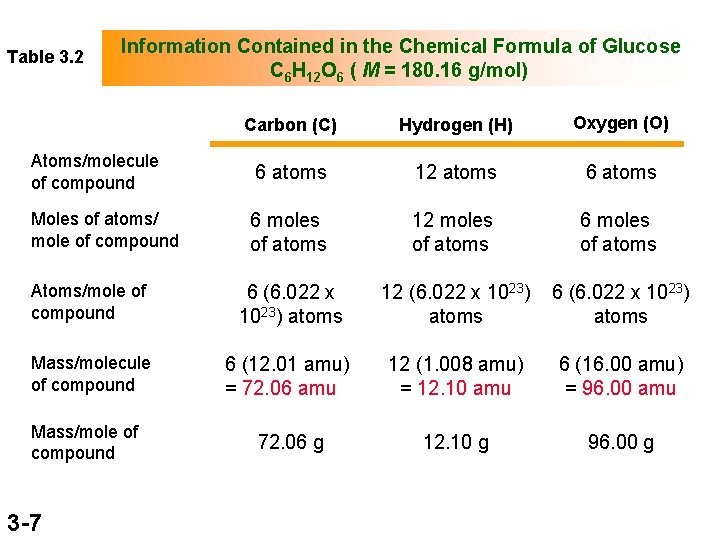
Table 3. 2 Information Contained in the Chemical Formula of Glucose C 6 H 12 O 6 ( M = 180. 16 g/mol) Carbon (C) Hydrogen (H) Oxygen (O) Atoms/molecule of compound 6 atoms 12 atoms 6 atoms Moles of atoms/ mole of compound 6 moles of atoms 12 moles of atoms 6 moles of atoms Atoms/mole of compound 6 (6. 022 x 1023) atoms 12 (6. 022 x 1023) atoms 6 (6. 022 x 1023) atoms Mass/molecule of compound 6 (12. 01 amu) = 72. 06 amu 12 (1. 008 amu) = 12. 10 amu 6 (16. 00 amu) = 96. 00 amu 72. 06 g 12. 10 g 96. 00 g Mass/mole of compound 3 -7

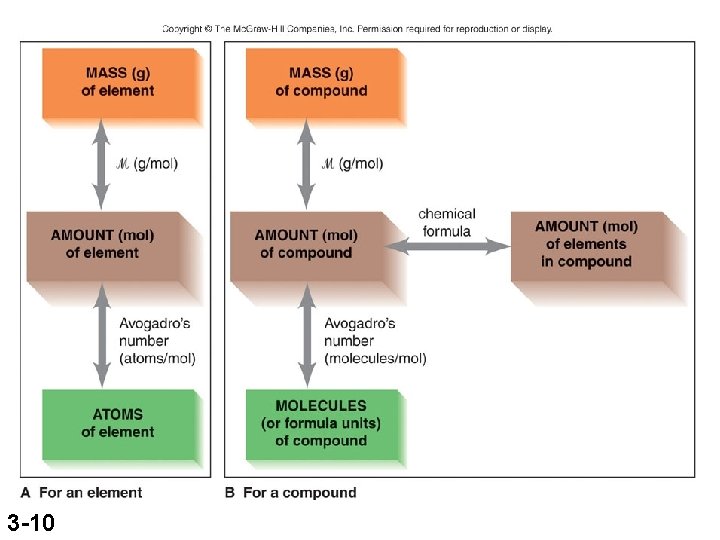
Interconverting Moles, Mass, and Number of Chemical Entities mass (g) = no. of moles x no. of moles = mass (g) x no. of grams 1 mol no. of grams no. of entities = no. of moles x 6. 022 x 1023 entities 1 mol no. of moles = no. of entities x 3 -8 1 mol 6. 022 x 1023 entities

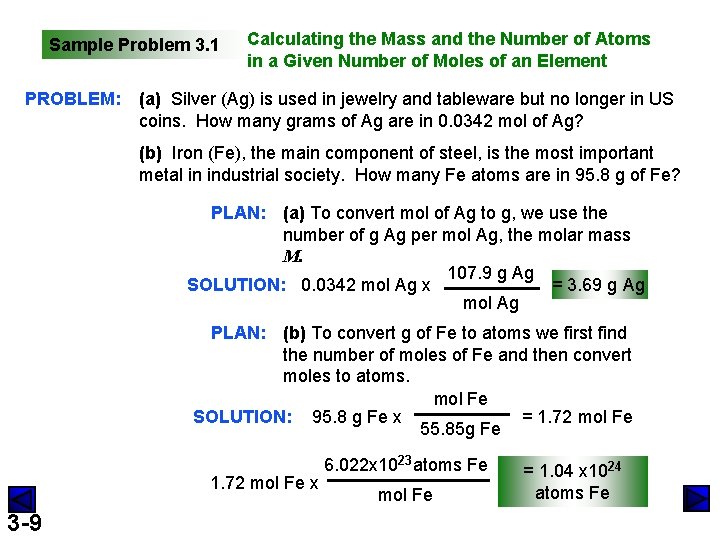
Sample Problem 3. 1 PROBLEM: Calculating the Mass and the Number of Atoms in a Given Number of Moles of an Element (a) Silver (Ag) is used in jewelry and tableware but no longer in US coins. How many grams of Ag are in 0. 0342 mol of Ag? (b) Iron (Fe), the main component of steel, is the most important metal in industrial society. How many Fe atoms are in 95. 8 g of Fe? PLAN: (a) To convert mol of Ag to g, we use the number of g Ag per mol Ag, the molar mass M. 107. 9 g Ag SOLUTION: 0. 0342 mol Ag x = 3. 69 g Ag mol Ag PLAN: (b) To convert g of Fe to atoms we first find the number of moles of Fe and then convert moles to atoms. mol Fe SOLUTION: 95. 8 g Fe x = 1. 72 mol Fe 55. 85 g Fe 1. 72 mol Fe x 3 -9 6. 022 x 1023 atoms Fe mol Fe = 1. 04 x 1024 atoms Fe

3 -10

Sample Problem 3. 2 PROBLEM: Calculating the Moles and Number of Formula Units in a Given Mass of a Compound Ammonium carbonate is white solid that decomposes with warming. Among its many uses, it is a component of baking powder, fire extinguishers, and smelling salts. How many formula units are in 41. 6 g of ammonium carbonate? PLAN: After writing the formula for the compound, we find M by adding the masses of the elements, convert the given mass (41. 6 g) to moles using M, and then convert moles to formula units using Avogadro’s number. SOLUTION: The formula is (NH 4)2 CO 3. M = (2 x 14. 01 g/mol N) + (8 x 1. 008 g/mol H + (12. 01 g/mol C) + (3 x 16. 00 g/mol O) = 96. 09 g/mol 41. 6 g (NH 4)2 CO 3 x 3 -11 mol (NH 4)2 CO 3 96. 09 g (NH 4)2 CO 3 x 6. 022 x 1023 formula units (NH 4)2 CO 3 mol (NH 4)2 CO 3 2. 61 x 1023 formula units (NH 4)2 CO 3 =

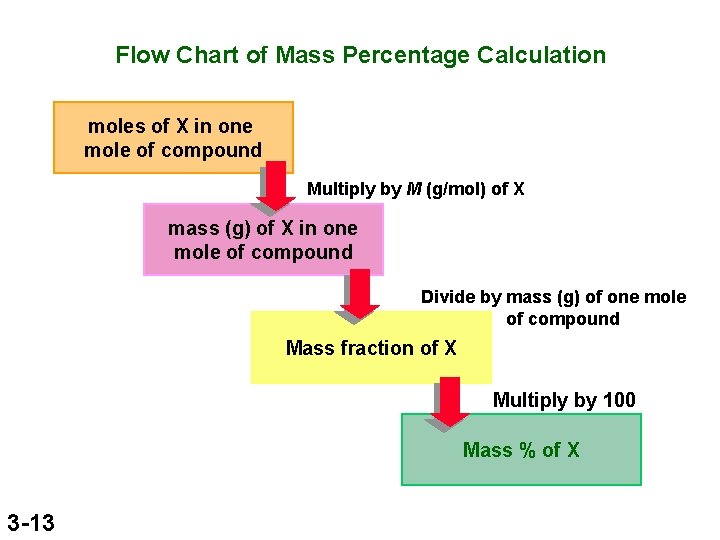
mass % of element X = atoms of X in formula x atomic mass of X (amu) x 100 molecular (or formula) mass of compound(amu) mass % of element X = moles of X in formula x molar mass of X (g/mol) mass (g) of 1 mole of compound 3 -12 x 100

Flow Chart of Mass Percentage Calculation moles of X in one mole of compound Multiply by M (g/mol) of X mass (g) of X in one mole of compound Divide by mass (g) of one mole of compound Mass fraction of X Multiply by 100 Mass % of X 3 -13

3 -14

3 -15

Empirical and Molecular Formulas Empirical Formula The simplest formula for a compound that agrees with the elemental analysis and gives rise to the smallest set of whole numbers of atoms. Molecular Formula The formula of the compound as it exists, it may be a multiple of the empirical formula. 3 -16

Sample Problem 3. 4 Determining the Empirical Formula from Masses of Elements PROBLEM: Elemental analysis of a sample of an ionic compound gave the following results: 2. 82 g of Na, 4. 35 g of Cl, and 7. 83 g of O. What are the empirical formula and name of the compound? PLAN: Find the relative number of moles of each element; divide by the lowest mole amount to find the relative mole ratios (empirical formula). SOLUTION: 2. 82 g Na x 4. 35 g Cl x 7. 83 g O x mol Na 22. 99 g Na mol Cl 35. 45 g Cl mol O 16. 00 g O Na 1 Cl 1 O 3. 98 3 -17 = 0. 123 mol Na = 0. 123 mol Cl = 0. 489 mol O Na. Cl. O 4 is sodium perchlorate.

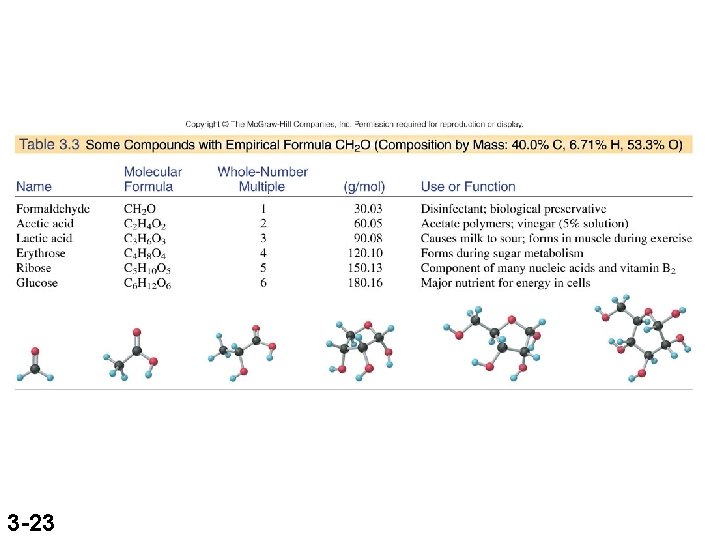
Sample Problem 3. 5 Determining a Molecular Formula from Elemental Analysis and Molar Mass PROBLEM: During physical activity, lactic acid (M = 90. 08 g/mol) forms in muscle tissue and is responsible for muscle soreness. Elemental analysis shows that it contains 40. 0 mass% C, 6. 71 mass% H, and 53. 3 mass% O. (a) Determine the empirical formula of lactic acid. (b) Determine the molecular formula. 3 -18

Sample Problem 3. 5 (continued) SOLUTION: 40. 0 g C x Assuming 100 g of lactic acid, the constituents are: mol C 12. 01 g C 3. 33 mol C C 3. 33 H 6. 66 O 3. 33 molar mass of lactate mass of CH 2 O 3 -19 6. 71 g H x mol H 1. 008 g H 53. 3 g O x 6. 66 mol H mol O 16. 00 g O 3. 33 mol O CH 2 O = empirical formula 90. 08 g 30. 03 g 3 C 3 H 6 O 3 is the molecular formula

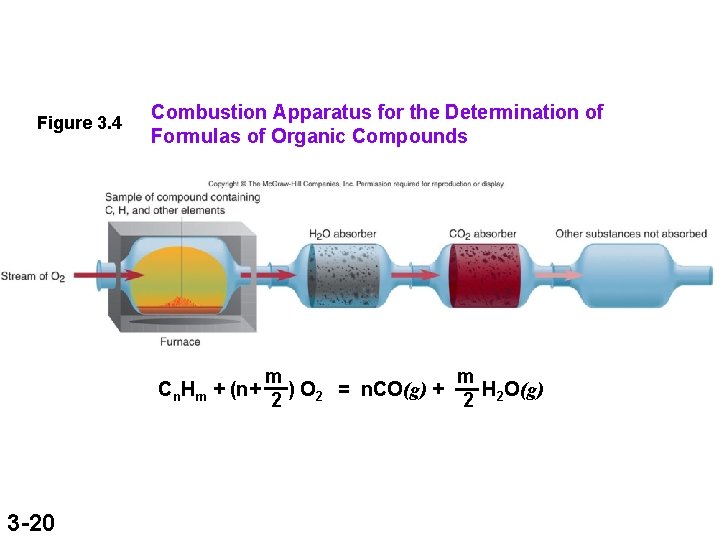
Figure 3. 4 Combustion Apparatus for the Determination of Formulas of Organic Compounds Cn. Hm + (n+ 3 -20 m m ) O 2 = n. CO(g) + H O(g) 2 2 2

Sample Problem 3. 6 PROBLEM: Determining a Molecular Formula from Combustion Analysis Vitamin C (M = 176. 12 g/mol) is a compound of C, H, and O found in many natural sources especially citrus fruits. When a 1. 000 g sample of vitamin C is placed in a combustion chamber and burned, the following data are obtained: mass of CO 2 absorber after combustion = 85. 35 g mass of CO 2 absorber before combustion = 83. 85 g mass of H 2 O absorber after combustion = 37. 96 g mass of H 2 O absorber before combustion = 37. 55 g What is the molecular formula of vitamin C? PLAN: difference (after-before) = mass of oxidized element find the mass of each element in its combustion product find the moles 3 -21 preliminary formula empirical formula molecular formula

Sample Problem 3. 6 (continued) SOLUTION: CO 2: 85. 35 g - 83. 85 g = 1. 50 g There are 12. 01 g C per mol CO 2 There are 2. 016 g H per mol H 2 O O must be the difference: 0. 409 g C 12. 01 g C C 1 H 1. 3 O 1 = 0. 0341 mol C C 3 H 4 O 3 H 2 O: 1. 50 g CO 2 x 0. 41 g H 2 O x 12. 01 g C = 0. 409 g C 44. 01 g CO 2 2. 016 g H = 0. 046 g H 18. 02 g H 2 O 1. 000 g - (0. 409 + 0. 046) = 0. 545 0. 046 g H 1. 008 g H = 0. 0461 mol H 176. 12 g/mol 88. 06 g 3 -22 37. 96 g - 37. 55 g = 0. 41 g 0. 545 g O 16. 00 g O = 2. 000 = 0. 0341 mol O C 6 H 8 O 6

3 -23

Table 3. 4 Two Compounds with Molecular Formula C 2 H 6 O Property Ethanol Dimethyl Ether M (g/mol) 46. 07 colorless melting point -117 0 C -138. 5 0 C boiling point 78. 5 0 C density (20 0 C) 0. 789 g/m. L (liquid) 0. 00195 g/m. L (gas) use intoxicant in alcoholic beverages refrigeration structural formulas and space-filling models 3 -24 -25 0 C

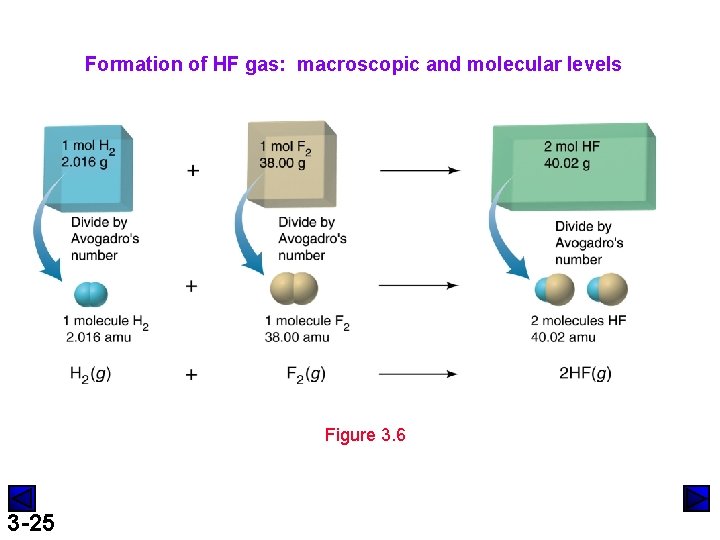
Formation of HF gas: macroscopic and molecular levels Figure 3. 6 3 -25

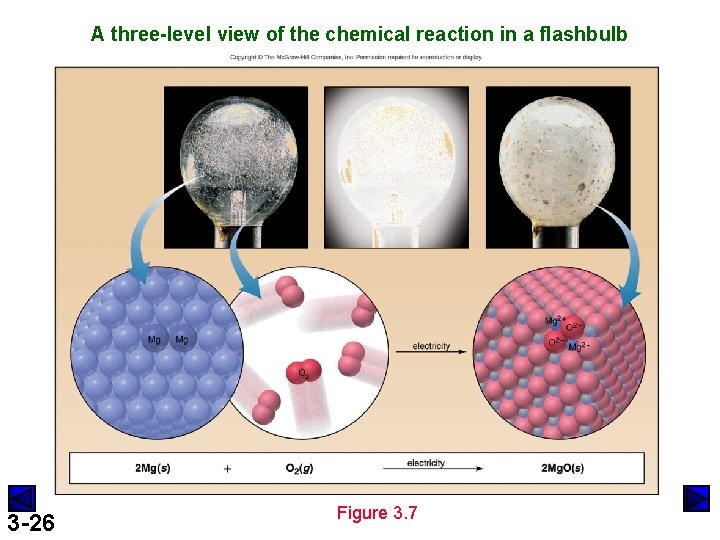
A three-level view of the chemical reaction in a flashbulb 3 -26 Figure 3. 7

Sample Problem 3. 7 PROBLEM: Balancing Chemical Equations Within the cylinders of a car’s engine, the hydrocarbon, octane (C 8 H 18), which is one of the many components of gasoline, mixes with oxygen from air and burns to form carbon dioxide and water vapor. Write a balanced equation for this reaction. PLAN: SOLUTION: translate the statement balance the atoms adjust the coefficients check the atom balance specify states of matter 3 -27 C 8 H 18 + O 2 CO 2 + H 2 O C 8 H 18 + O 2 8 CO 2 + 9 H 2 O C 8 H 18 + 25/2 O 2 8 CO 2 + 9 H 2 O 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O 2 C 8 H 18(l) + 25 O 2 (g) 16 CO 2 (g) + 18 H 2 O (g)

3 -28

Sample Problem 3. 8 PROBLEM: Calculating Amounts of Reactants and Products In a lifetime, the average American uses 1750 lb (794 kg) of copper in coins, plumbing, and wiring. Copper is obtained from sulfide ores, such as chalcocite, or copper(I) sulfide, by a multistage process. After an initial grinding step, the first stage is to “roast” the ore (heat it strongly with oxygen gas) to form powdered copper(I) oxide and gaseous sulfur dioxide. (a) How many moles of oxygen are required to roast 10. 0 mol of copper(I) sulfide? (b) How many grams of sulfur dioxide are formed when 10. 0 mol of copper(I) sulfide are roasted? (c) How many kilograms of oxygen are required to form 2. 86 kg of copper(I) oxide? PLAN: write and balance equation find mols O 2 3 -29 find mols SO 2 find mols Cu 2 O find g SO 2 find mols O 2 find kg O 2

Sample Problem 3. 8 SOLUTION: (continued) 2 Cu 2 S(s) + 3 O 2(g) (a) 10. 0 mol Cu 2 S x (b) 10. 0 mol Cu 2 S x (c) 2. 86 kg Cu 2 O x 3 mol O 2 2 mol Cu 2 S 2 mol SO 2 2 Cu 2 O(s) + 2 SO 2(g) = 15. 0 mol O 2 x 64. 07 g SO 2 2 mol Cu 2 S mol SO 2 103 g Cu 2 O mol Cu 2 O kg Cu 2 O x = 641 g SO 2 143. 10 g Cu 2 O = 20. 0 mol Cu 2 O 3 mol O 2 32. 00 g O 2 kg O 2 20. 0 mol Cu 2 O x x x 2 mol Cu 2 O mol O 2 103 g O 2 3 -30 = 0. 960 kg O 2

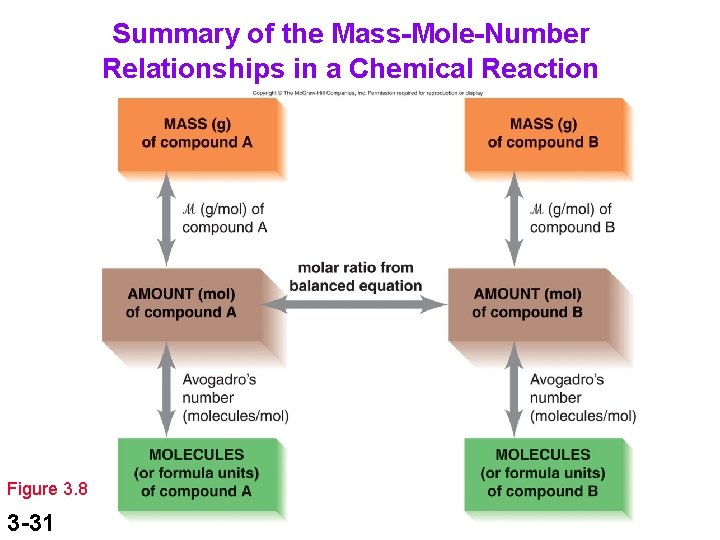
Summary of the Mass-Mole-Number Relationships in a Chemical Reaction Figure 3. 8 3 -31

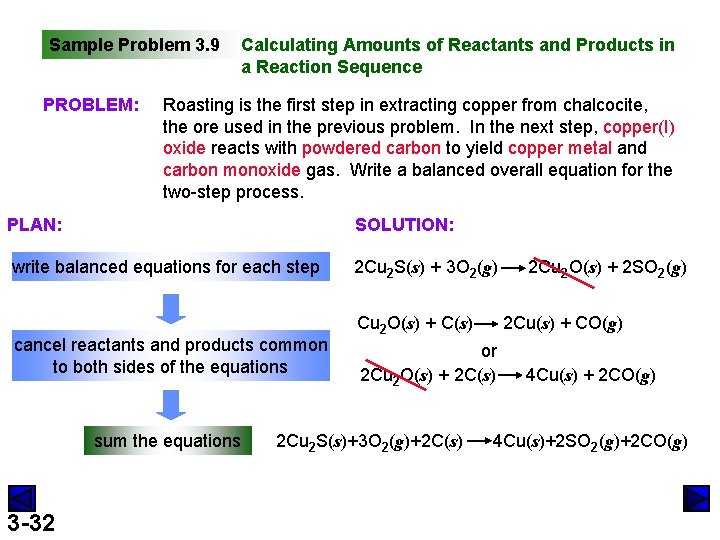
Sample Problem 3. 9 PROBLEM: Calculating Amounts of Reactants and Products in a Reaction Sequence Roasting is the first step in extracting copper from chalcocite, the ore used in the previous problem. In the next step, copper(I) oxide reacts with powdered carbon to yield copper metal and carbon monoxide gas. Write a balanced overall equation for the two-step process. PLAN: SOLUTION: write balanced equations for each step 2 Cu 2 S(s) + 3 O 2(g) cancel reactants and products common to both sides of the equations sum the equations 3 -32 Cu 2 O(s) + C(s) 2 Cu(s) + CO(g) or 2 Cu 2 O(s) + 2 C(s) 2 Cu 2 S(s)+3 O 2(g)+2 C(s) 2 Cu 2 O(s) + 2 SO 2(g) 4 Cu(s) + 2 CO(g) 4 Cu(s)+2 SO 2(g)+2 CO(g)

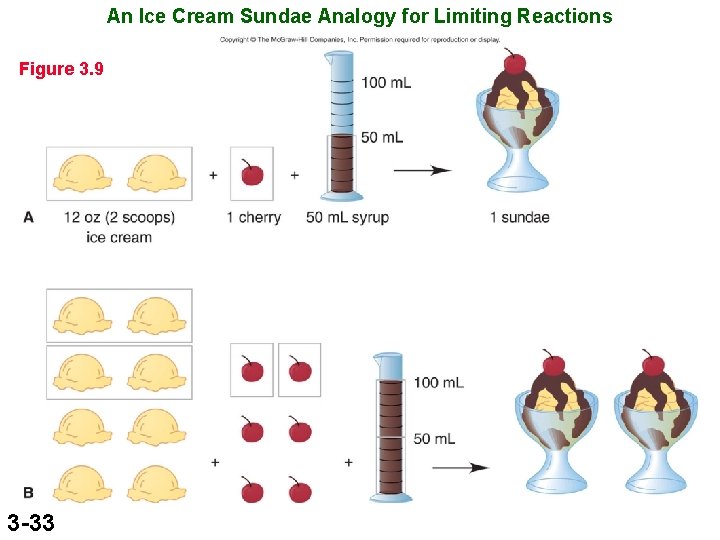
An Ice Cream Sundae Analogy for Limiting Reactions Figure 3. 9 3 -33

Sample Problem 3. 10 Calculating Amounts of Reactant and Product in Reactions Involving a Limiting Reactant PROBLEM: A fuel mixture used in the early days of rocketry was composed of two liquids, hydrazine (N 2 H 4) and dinitrogen tetraoxide (N 2 O 4), which ignite on contact to form nitrogen gas and water vapor. How many grams of nitrogen gas (N 2) form when 1. 00 x 102 g of N 2 H 4 and 2. 00 x 102 g of N 2 O 4 are mixed? PLAN: Start with a balanced chemical equation and find the number of moles of reactants; identify limiting reagent; determine grams of N 2 formed. mass of N 2 H 4 mass of N 2 O 4 divide by M mol of N 2 H 4 multiply by M mol of N 2 O 4 molar ratio mol of N 2 3 -34 limiting mol N 2 mol of N 2 g N 2

Sample Problem 3. 10 (continued) SOLUTION: 1. 00 x 102 g N 2 H 4 x 3. 12 mol N 2 H 4 x 2. 00 x 102 g N 2 O 4 x 2. 17 mol N 2 O 4 x 3 -35 2 N 2 H 4(l) + N 2 O 4(l) mol N 2 H 4 32. 05 g N 2 H 4 3 mol N 2 2 mol N 2 H 4 92. 02 g N 2 O 4 mol N 2 O 4 = 3. 12 mol N 2 H 4 = 4. 68 mol N 2 O 4 3 mol N 2 3 N 2(g) + 4 H 2 O(l) N 2 H 4 is the limiting reactant because it produces less product, N 2, than does N 2 O 4. = 2. 17 mol N 2 O 4 = 6. 51 mol N 2 4. 68 mol N 2 x 28. 02 g N 2 mol N 2 = 131 g N 2

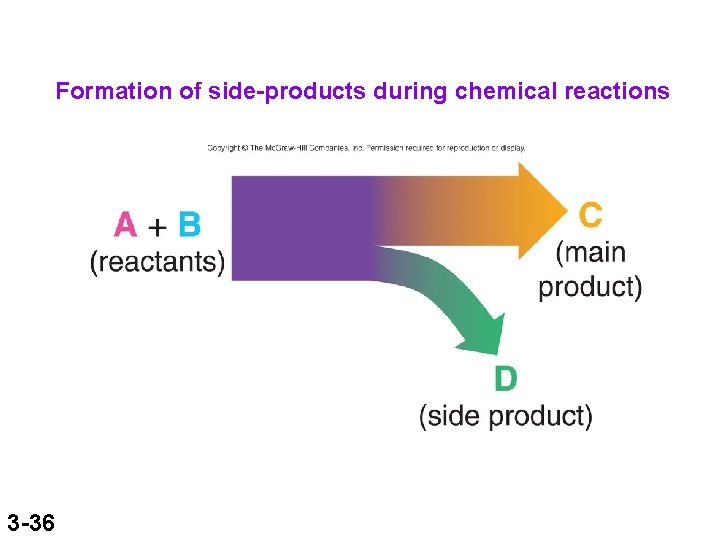
Formation of side-products during chemical reactions 3 -36

Sample Problem 3. 11 Calculating Percent Yield PROBLEM: Silicon carbide (Si. C) is an important ceramic material that is made by allowing sand (silicon dioxide, Si. O 2) to react with powdered carbon at high temperature. Carbon monoxide is also formed. When 100. 0 kg of sand are processed, 51. 4 kg of Si. C are recovered. What is the percent yield of Si. C in this process? PLAN: write balanced equation find mol reactant & product find g product predicted SOLUTION: Si. O 2(s) + 3 C(s) 100. 0 kg Si. O 2 x 103 g Si. O 2 kg Si. O 2 51. 4 kg 66. 73 kg 3 -37 x mol Si. O 2 = 1664 mol 60. 09 g Si. O 2 mol Si. O 2 = mol Si. C = 1664 mol Si. C x percent yield Si. C(s) + 2 CO(g) 40. 10 g Si. C mol Si. C x kg 103 g x 100 = 77. 0% = 66. 73 kg

Sample Problem 3. 12 Calculating the Molarity of a Solution PROBLEM: PLAN: Hydrobromic acid (HBr) is a solution of hydrogen bromide gas in water. Calculate the molarity of a hydrobromic acid solution if 455 m. L contains 1. 80 moles of hydrogen bromide. Molarity (M) is the number of moles of solute per liter of solution. mol of HBr divide by volume concentration (mol/m. L) HBr 103 m. L = 1 L molarity (mol/L) HBr 3 -38 SOLUTION: 1. 80 mol HBr 455 m. L soln x 1000 m. L 1 L = 3. 96 M

Sample Problem 3. 13 Calculating Mass of Solute in a Given Volume of Solution PROBLEM: How many grams of solute are found in 1. 75 L of a 0. 460 M solution of sodium monohydrogen phosphate? PLAN: Molarity is the number of moles of solute per liter of solution. Knowing the molarity and volume allows us to find the number of moles and then the number of grams of solute. The molecular formula of the solute is Na 2 HPO 4. volume of soln SOLUTION: multiply by M moles of solute multiply by M grams of solute 1. 75 L x 0. 460 moles 1 L = 0. 805 mol Na 2 HPO 4 x 141. 96 g Na 2 HPO 4 mol Na 2 HPO 4 = 114 g Na 2 HPO 4 3 -39

Sample Problem 3. 14 PROBLEM: PLAN: Preparing a Dilute Solution from a Concentrated Solution Isotonic saline is a 0. 15 M aqueous solution of Na. Cl that simulates the total concentration of ions found in many cellular fluids. Its uses range from a cleaning rinse for contact lenses to a washing medium for red blood cells (erythrocytes). How would you prepare 0. 80 L of isotonic saline from a 6. 0 M stock solution? The number of moles of solute does not change during the dilution but volume does. The new volume will be the sum of the two volumes, that is, the total final volume. Mdil x Vdil = # mol solute = Mconc x Vconc SOLUTION: 0. 80 L soln x 0. 12 mol Na. Cl x 3 -40 0. 15 mol Na. Cl L solnconc 6 mol Na. Cl = 0. 12 mol Na. Cl = 0. 020 L soln

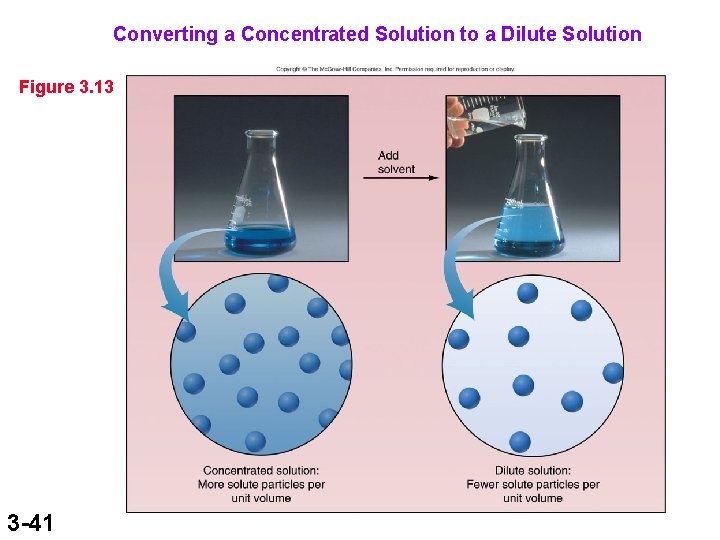
Converting a Concentrated Solution to a Dilute Solution Figure 3. 13 3 -41

Figure 3. 11 3 -42

Sample Problem 3. 15 Calculating Amounts of Reactants and Products for a Reaction in Solution PROBLEM: Specialized cells in the stomach release HCl to aid digestion. If they release too much, the excess can be neutralized with antacids. A common antacid contains magnesium hydroxide, which reacts with the HCl to form water and magnesium chloride solution. As a government chemist testing commercial antacids, you use 0. 10 M HCl to simulate the acid concentration in the stomach. How many liters of “stomach acid” react with a tablet containing 0. 10 g of magnesium hydroxide? PLAN: Write a balanced equation for the reaction; find the moles of Mg(OH)2; determine the mole ratio of reactants and products; use moles to convert to molarity. mass Mg(OH)2 L HCl divide by M mol Mg(OH)2 mol HCl mol ratio 3 -43 divide by M

Sample Problem 3. 15 SOLUTION: (continued) Mg(OH)2(s) + 2 HCl(aq) 0. 10 g Mg(OH)2 x mol Mg(OH)2 58. 33 g Mg(OH)2 1. 7 x 10 -3 mol Mg(OH)2 x 3. 4 x 10 -3 mol HCl x 1 mol Mg(OH)2 0. 10 mol HCl 3 -44 = 1. 7 x 10 -3 mol Mg(OH)2 2 mol HCl 1 L Mg. Cl 2(aq) + 2 H 2 O(l) = 3. 4 x 10 -3 mol HCl = 3. 4 x 10 -2 L HCl

Sample Problem 3. 16 Solving Limiting Reactant Problems for Reactions in Solution PROBLEM: PLAN: 3 -45 Mercury and its compounds have many uses, from filling teeth (as an alloy with silver, copper, and tin) to the industrial production of chlorine. Because of their toxicity, however, soluble mercury compounds, such mercury(II) nitrate, must be removed from industrial wastewater. One removal method reacts the wastewater with sodium sulfide solution to produce solid mercury(II) sulfide and sodium nitrate solution. In a laboratory simulation, 0. 050 L of 0. 010 M mercury(II) nitrate reacts with 0. 020 L of 0. 10 M sodium sulfide. How many grams of mercury(II) sulfide form? Write a balanced chemical equation for the reaction. Since this is a problem concerning a limiting reactant, we find the amount of product that would be made from each reactant. We then choose the reactant that gives the lesser amount of product.

Sample Problem 3. 16 (continued) Hg(NO 3)2(aq) + Na 2 S(aq) SOLUTION: 0. 050 L Hg(NO 3)2 x 0. 010 mol/L x 0. 020 L Na 2 S x 0. 10 mol/L x Hg. S(s) + 2 Na. NO 3(aq) 1 mol Hg. S 1 mol Hg(NO 3)2 1 mol Hg. S 1 mol Na 2 S = 5. 0 x 10 -4 mol Hg. S = 2. 0 x 10 -3 mol Hg. S Hg(NO 3)2 is the limiting reagent. 5. 0 x 3 -46 10 -4 mol Hg. S x 232. 7 g Hg. S 1 mol Hg. S = 0. 12 g Hg. S

Laboratory Preparation of Molar Solutions Figure 3. 12 3 -47

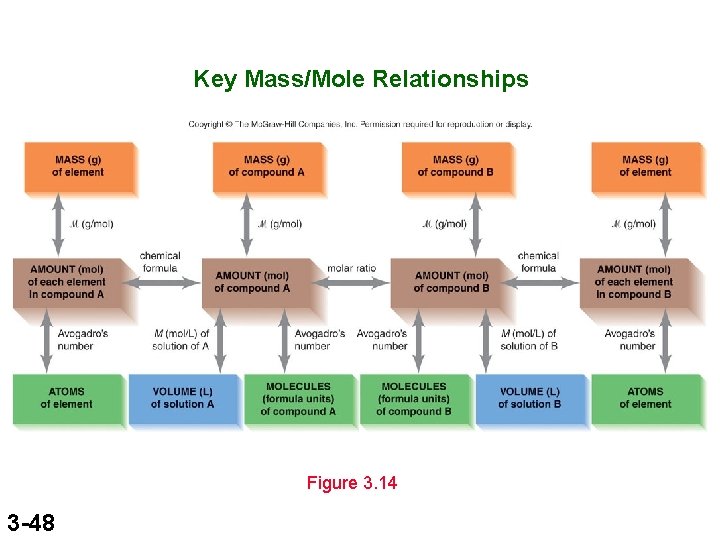
Key Mass/Mole Relationships Figure 3. 14 3 -48