Chapter 3 Statistical Process Control Russell and Taylor








































- Slides: 67

Chapter 3 Statistical Process Control Russell and Taylor Operations and Supply Chain Management, 8 th Edition



Lecture Outline • • Basics of Statistical Process Control Charts for Attributes Control Charts for Variables Control Chart Patterns SPC with Excel and OM Tools Process Capability © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -4

Learning Objectives • Explain when and how to use statistical process control to ensure the quality of products and services • Discuss the rationale and procedure for constructing attribute and variable control charts • Utilize appropriate control charts to determine if a process is in-control • Identify control chart patterns and describe appropriate data collection • Assess the process capability of a process © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -5

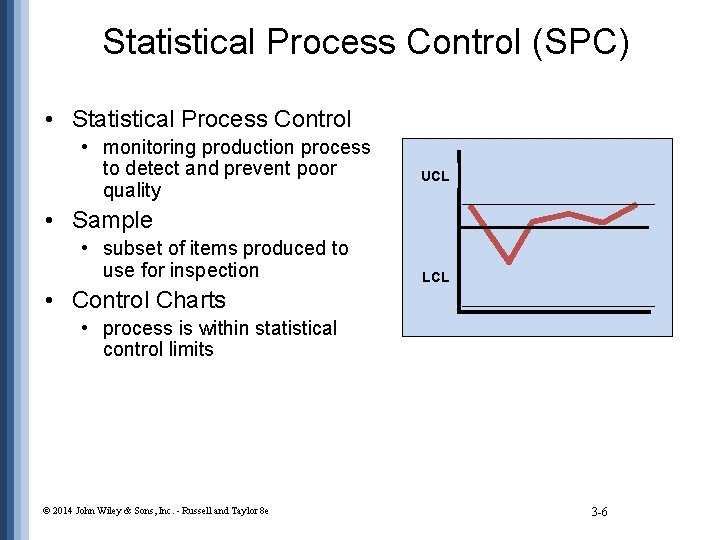
Statistical Process Control (SPC) • Statistical Process Control • monitoring production process to detect and prevent poor quality UCL • Sample • subset of items produced to use for inspection LCL • Control Charts • process is within statistical control limits © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -6

Process Variability • Random • inherent in a process • depends on equipment and machinery, engineering, operator, and system of measurement • natural occurrences © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e • Non-Random • special causes • identifiable and correctable • include equipment out of adjustment, defective materials, changes in parts or materials, broken machinery or equipment, operator fatigue or poor work methods, or errors due to lack of training 3 -7

SPC in Quality Management • SPC uses • Is the process in control? • Identify problems in order to make improvements • Contribute to the TQM goal of continuous improvement © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -8

Quality Measures: Attributes and Variables • Attribute • A characteristic which is evaluated with a discrete response • good/bad; yes/no; correct/incorrect • Variable measure • A characteristic that is continuous and can be measured • Weight, length, voltage, volume © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -9

SPC Applied to Services • Nature of defects is different in services • Service defect is a failure to meet customer requirements • Monitor time and customer satisfaction © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -10

SPC Applied to Services • Hospitals • timeliness & quickness of care, staff responses to requests, accuracy of lab tests, cleanliness, courtesy, accuracy of paperwork, speed of admittance & checkouts • Grocery stores • waiting time to check out, frequency of out-of-stock items, quality of food items, cleanliness, customer complaints, checkout register errors • Airlines • flight delays, lost luggage & luggage handling, waiting time at ticket counters & check-in, agent & flight attendant courtesy, accurate flight information, cabin cleanliness & maintenance © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -11

SPC Applied to Services • Fast-food restaurants • waiting time for service, customer complaints, cleanliness, food quality, order accuracy, employee courtesy • Catalogue-order companies • order accuracy, operator knowledge & courtesy, packaging, delivery time, phone order waiting time • Insurance companies • billing accuracy, timeliness of claims processing, agent availability & response time © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -12

Where to Use Control Charts • Process • Has a tendency to go out of control • Is particularly harmful and costly if it goes out of control • Examples • At beginning of process because of waste to begin production process with bad supplies • Before a costly or irreversible point, after which product is difficult to rework or correct • Before and after assembly or painting operations that might cover defects • Before the outgoing final product or service is delivered © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -13

Control Charts • A graph that monitors process quality • Control limits • upper and lower bands of a control chart • Attributes chart • p-chart • c-chart • Variables chart • mean (x bar – chart) • range (R-chart) © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -14

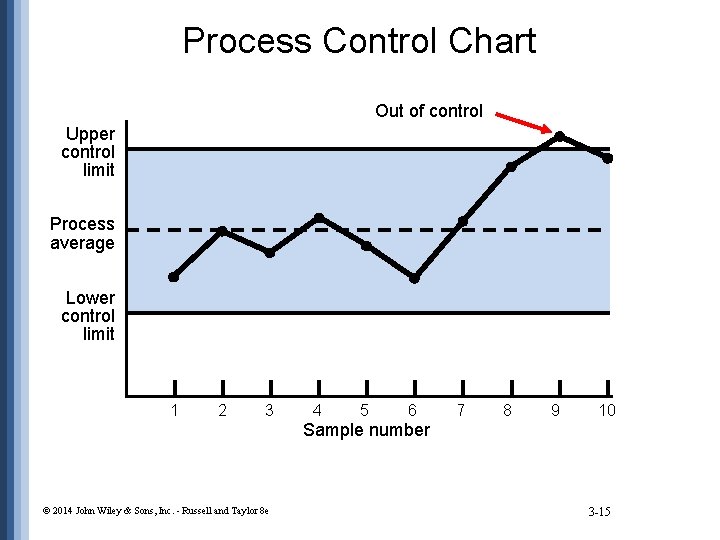
Process Control Chart Out of control Upper control limit Process average Lower control limit 1 2 3 4 5 6 7 8 9 10 Sample number © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -15

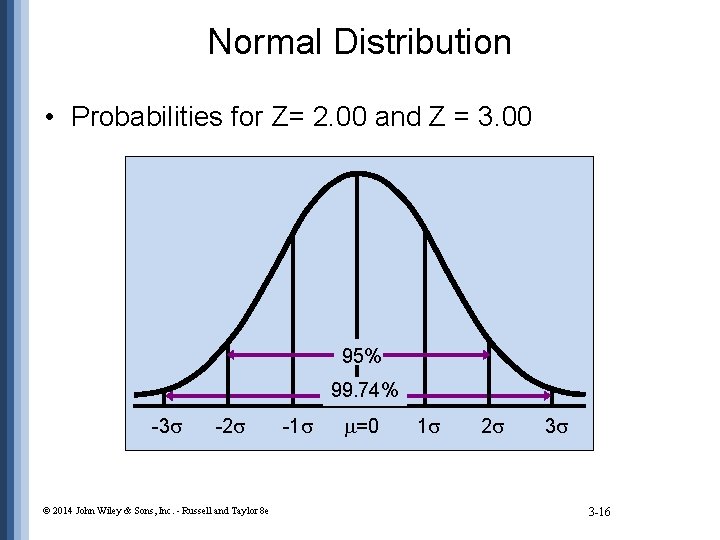
Normal Distribution • Probabilities for Z= 2. 00 and Z = 3. 00 95% 99. 74% -3 -2 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e -1 =0 1 2 3 3 -16

A Process Is in Control If … 1. … no sample points outside limits 2. … most points near process average 3. … about equal number of points above and below centerline 4. … points appear randomly distributed © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -17

Control Charts for Attributes • p-chart • uses portion defective in a sample • c-chart • uses number of defects (non-conformities) in a sample © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -18

p-Chart UCL = p + z p LCL = p - z p z = number of standard deviations from process average p = sample proportion defective; estimates process mean p = standard deviation of sample proportion p = © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e p(1 - p) n 3 -19

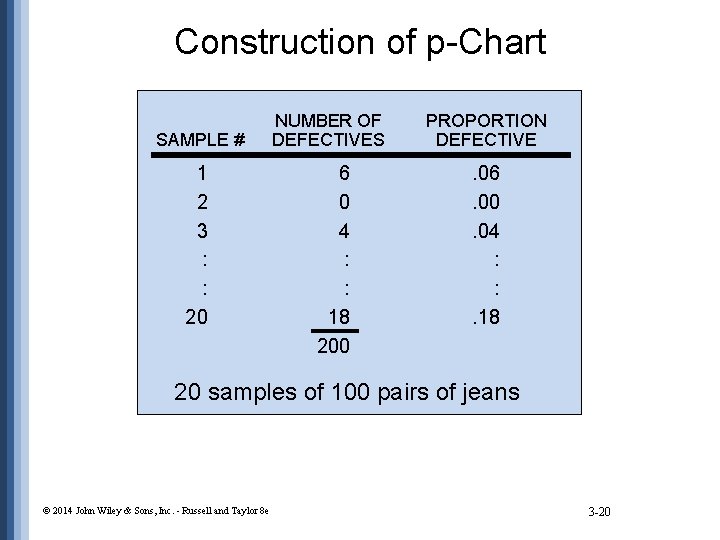
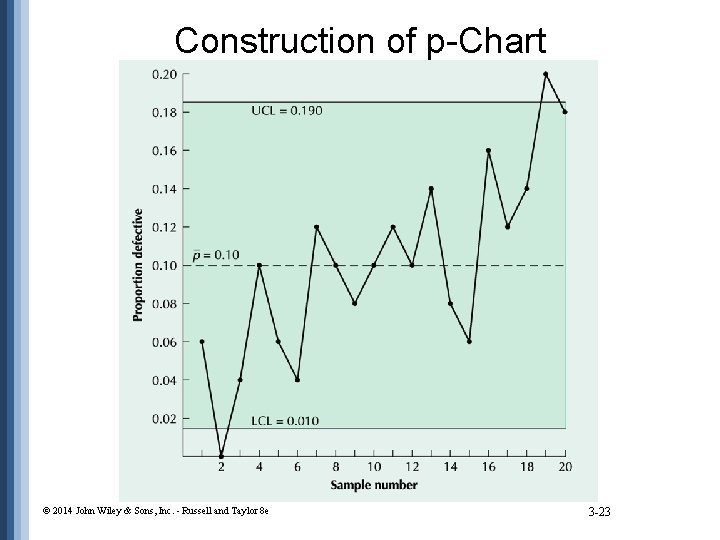
Construction of p-Chart SAMPLE # 1 2 3 : : 20 NUMBER OF DEFECTIVES PROPORTION DEFECTIVE 6 0 4 : : 18 200 . 06. 00. 04 : : . 18 20 samples of 100 pairs of jeans © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -20

Construction of p-Chart p= total defectives total sample observations = p(1 - p) = n UCL = p + z UCL = LCL = p - z p(1 - p) = n LCL = © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -21

Construction of p-Chart p= total defectives total sample observations = 200 / 20(100) = 0. 10 p(1 - p) = 0. 10 + 3 n UCL = p + z 0. 10(1 - 0. 10) 100 UCL = 0. 190 LCL = p - z p(1 - p) = 0. 10 - 3 n 0. 10(1 - 0. 10) 100 LCL = 0. 010 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -22

Construction of p-Chart © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -23

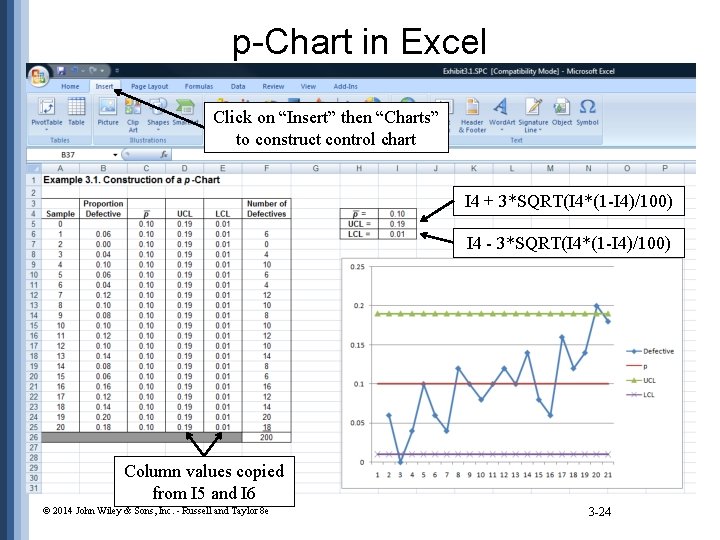
p-Chart in Excel Click on “Insert” then “Charts” to construct control chart I 4 + 3*SQRT(I 4*(1 -I 4)/100) I 4 - 3*SQRT(I 4*(1 -I 4)/100) Column values copied from I 5 and I 6 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -24

c-Chart UCL = c + z c LCL = c - z c c = c where c = number of defects per sample © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -25

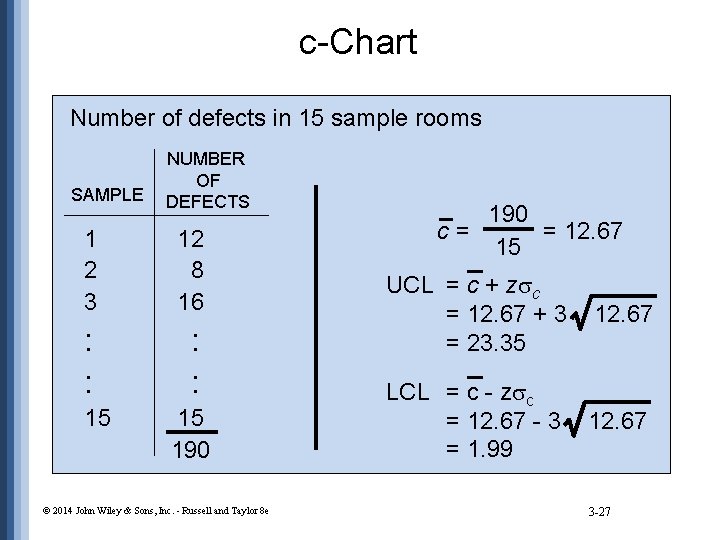
c-Chart Number of defects in 15 sample rooms SAMPLE NUMBER OF DEFECTS c= 1 2 3 12 8 16 UCL = c + z c : : LCL = c - z c 15 15 190 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -26

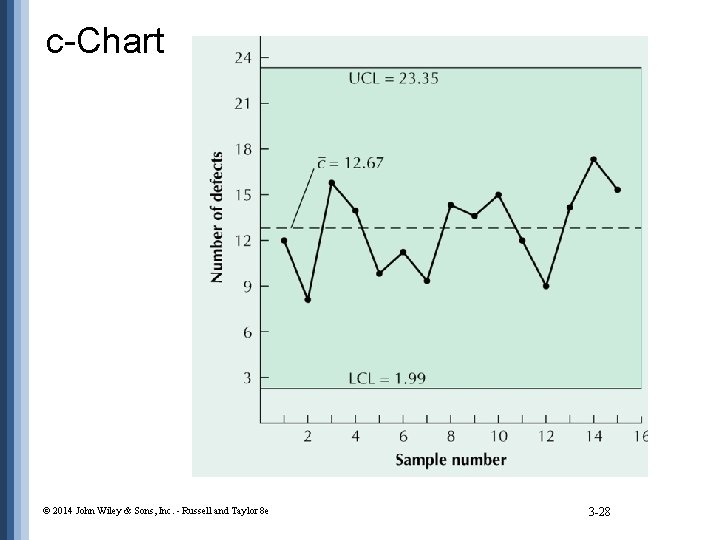
c-Chart Number of defects in 15 sample rooms SAMPLE NUMBER OF DEFECTS 1 2 3 12 8 16 : : 15 15 190 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 190 c= = 12. 67 15 UCL = c + z c = 12. 67 + 3 = 23. 35 12. 67 LCL = c - z c = 12. 67 - 3 = 1. 99 12. 67 3 -27

c-Chart © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -28

Control Charts for Variables § Range chart ( R-Chart ) § Plot sample range (variability) § Mean chart ( x -Chart ) § Plot sample averages © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -29

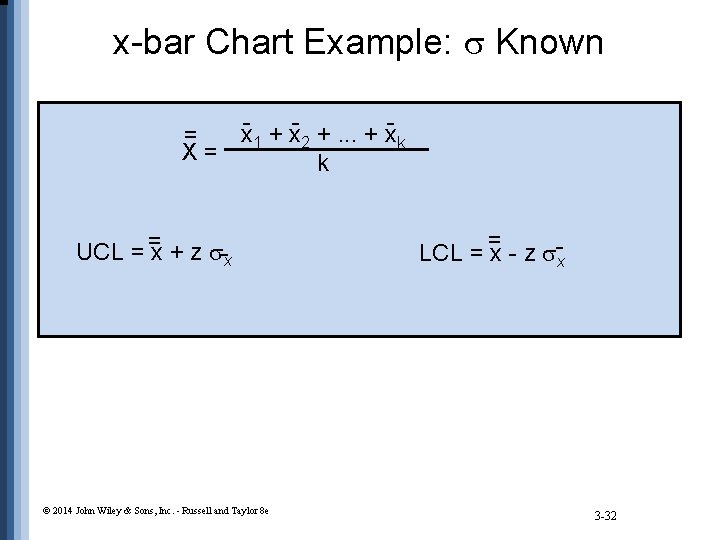
x-bar Chart: Known UCL = =x + z x. LCL = = x - z -x Where - + x- +. . . + xx = 2 k X= 1 k = process standard deviation x = standard deviation of sample means = / n k = number of samples (subgroups) n = sample size (number of observations) © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -30

x-bar Chart Example: Known Observations(Slip-Ring Diameter, cm) n Sample k 1 2 3 4 5 x- We know σ =. 08 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -31

x-bar Chart Example: Known x 1 + x 2 +. . . + xk = X= k UCL = =x + z -x © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e = LCL = x - z -x 3 -32

x-bar Chart Example: Known = 50. 09 X = _____ = 5. 01 10 = UCL = x + z -x = 5. 01 + 3(. 08 / 10) = 5. 09 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e LCL = =x - z -x = 5. 01 - 3(. 08 / 10) = 4. 93 3 -33

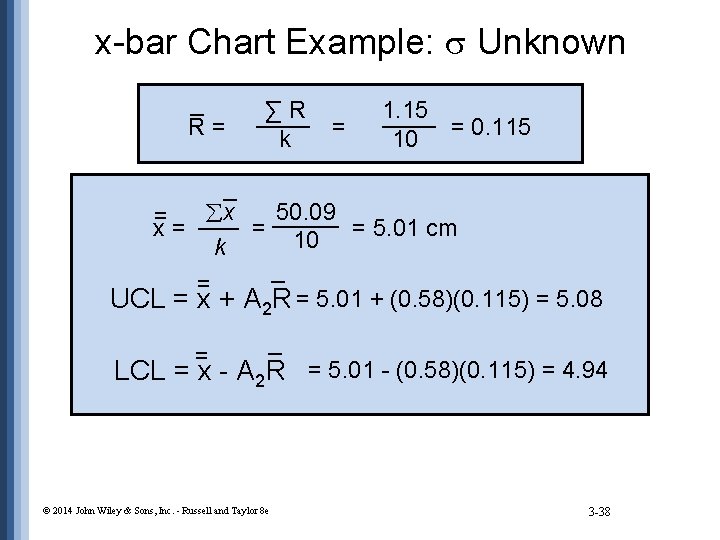
x-bar Chart Example: Unknown UCL = x += A 2 R _ _ LCL== x - A 2 R where = x = average of the sample means _ R = average range value © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -34

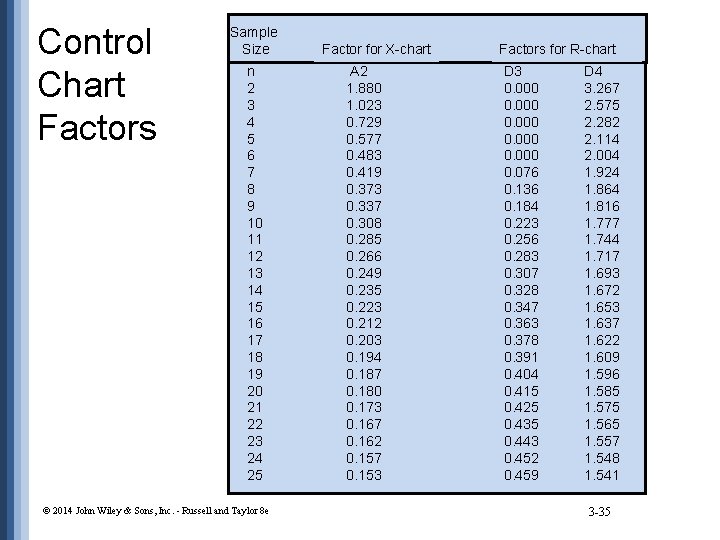
Control Chart Factors Sample Size n 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e Factor for X-chart A 2 1. 880 1. 023 0. 729 0. 577 0. 483 0. 419 0. 373 0. 337 0. 308 0. 285 0. 266 0. 249 0. 235 0. 223 0. 212 0. 203 0. 194 0. 187 0. 180 0. 173 0. 167 0. 162 0. 157 0. 153 Factors for R-chart D 3 0. 000 0. 076 0. 136 0. 184 0. 223 0. 256 0. 283 0. 307 0. 328 0. 347 0. 363 0. 378 0. 391 0. 404 0. 415 0. 425 0. 435 0. 443 0. 452 0. 459 D 4 3. 267 2. 575 2. 282 2. 114 2. 004 1. 924 1. 864 1. 816 1. 777 1. 744 1. 717 1. 693 1. 672 1. 653 1. 637 1. 622 1. 609 1. 596 1. 585 1. 575 1. 565 1. 557 1. 548 1. 541 3 -35

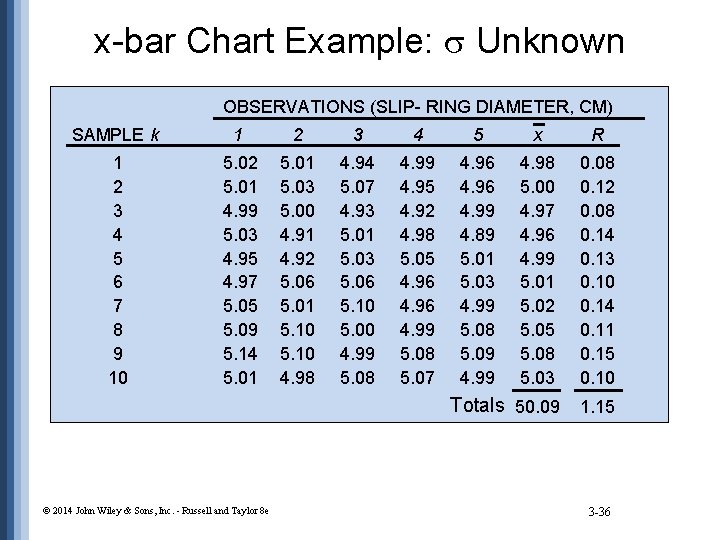
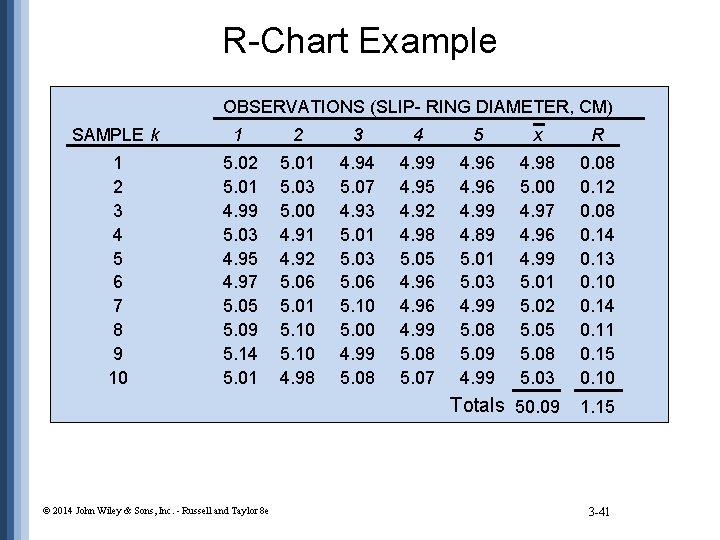
x-bar Chart Example: Unknown OBSERVATIONS (SLIP- RING DIAMETER, CM) SAMPLE k 1 2 3 4 5 x R 1 2 3 4 5 6 7 8 9 10 5. 02 5. 01 4. 99 5. 03 4. 95 4. 97 5. 05 5. 09 5. 14 5. 01 5. 03 5. 00 4. 91 4. 92 5. 06 5. 01 5. 10 4. 98 4. 94 5. 07 4. 93 5. 01 5. 03 5. 06 5. 10 5. 00 4. 99 5. 08 4. 99 4. 95 4. 92 4. 98 5. 05 4. 96 4. 99 5. 08 5. 07 4. 96 4. 99 4. 89 5. 01 5. 03 4. 99 5. 08 5. 09 4. 98 5. 00 4. 97 4. 96 4. 99 5. 01 5. 02 5. 05 5. 08 5. 03 0. 08 0. 12 0. 08 0. 14 0. 13 0. 10 0. 14 0. 11 0. 15 0. 10 Totals 50. 09 1. 15 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -36

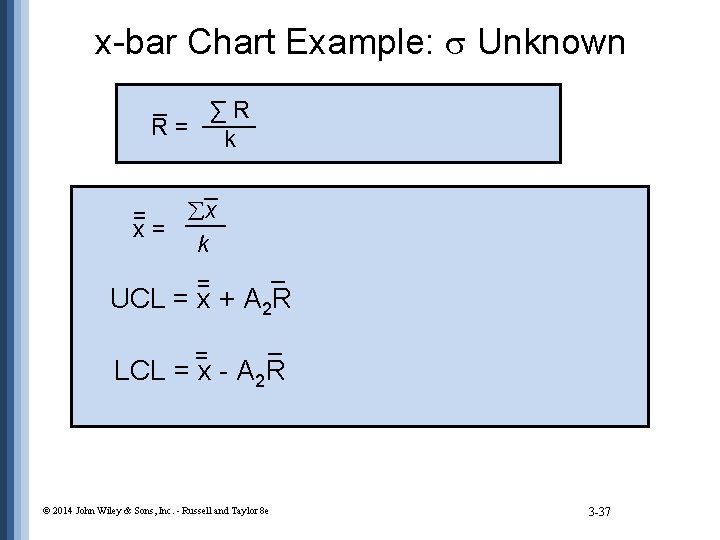
x-bar Chart Example: Unknown _ ∑R ____ R= k _ åx ___ = x= k _ = UCL = x + A 2 R = _ LCL = x - A 2 R © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -37

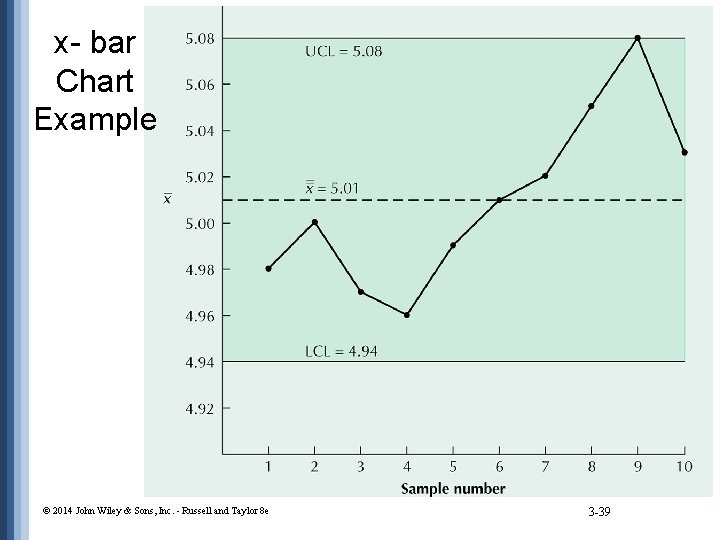
x-bar Chart Example: Unknown _ R= ∑R ____ = k 1. 15 ____ 10 = 0. 115 _ 50. 09 åx _____ = ___ x= = = 5. 01 cm 10 k _ = UCL = x + A 2 R = 5. 01 + (0. 58)(0. 115) = 5. 08 = _ LCL = x - A 2 R = 5. 01 - (0. 58)(0. 115) = 4. 94 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -38

x- bar Chart Example © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -39

R- Chart UCL = D 4 R LCL = D 3 R åR R= k Where R = range of each sample k = number of samples (sub groups) © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -40

R-Chart Example OBSERVATIONS (SLIP- RING DIAMETER, CM) SAMPLE k 1 2 3 4 5 x R 1 2 3 4 5 6 7 8 9 10 5. 02 5. 01 4. 99 5. 03 4. 95 4. 97 5. 05 5. 09 5. 14 5. 01 5. 03 5. 00 4. 91 4. 92 5. 06 5. 01 5. 10 4. 98 4. 94 5. 07 4. 93 5. 01 5. 03 5. 06 5. 10 5. 00 4. 99 5. 08 4. 99 4. 95 4. 92 4. 98 5. 05 4. 96 4. 99 5. 08 5. 07 4. 96 4. 99 4. 89 5. 01 5. 03 4. 99 5. 08 5. 09 4. 98 5. 00 4. 97 4. 96 4. 99 5. 01 5. 02 5. 05 5. 08 5. 03 0. 08 0. 12 0. 08 0. 14 0. 13 0. 10 0. 14 0. 11 0. 15 0. 10 Totals 50. 09 1. 15 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -41

R-Chart Example _ UCL = D 4 R = _ LCL = D 3 R = Retrieve chart factors D 3 and D 4 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -42

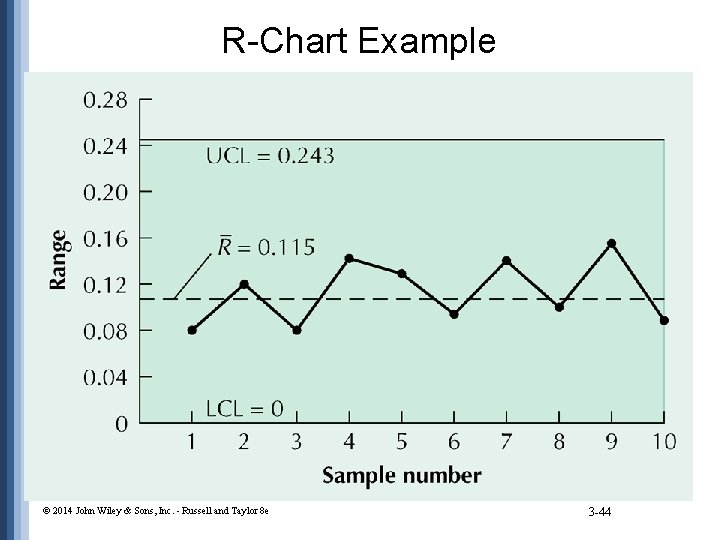
R-Chart Example _ UCL = D 4 R = 2. 11(0. 115) = 0. 243 _ LCL = D 3 R = 0(0. 115) = 0 Retrieve chart factors D 3 and D 4 © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -43

R-Chart Example © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -44

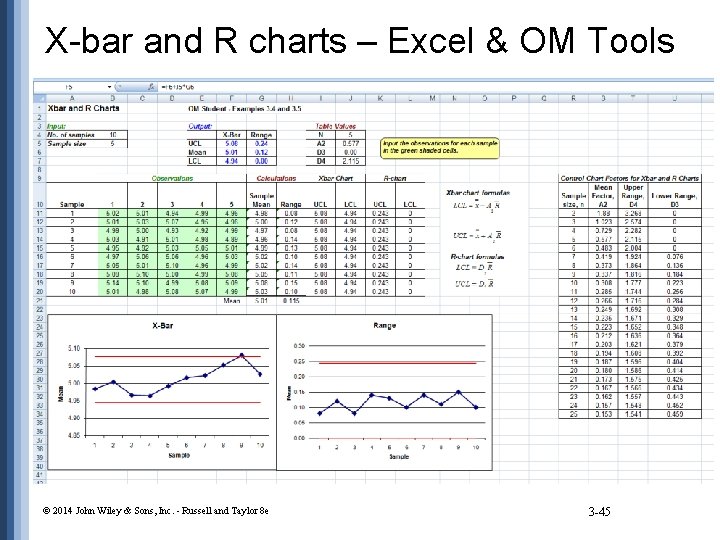
X-bar and R charts – Excel & OM Tools © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -45

Using x- bar and R-Charts Together • Process average and process variability must be in control • Samples can have very narrow ranges, but sample averages might be beyond control limits • Or, sample averages may be in control, but ranges might be out of control • An R-chart might show a distinct downward trend, suggesting some nonrandom cause is reducing variation © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -46

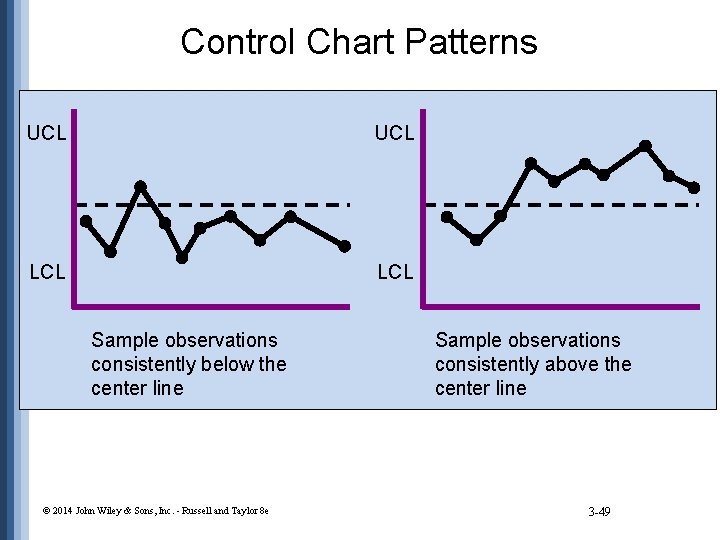
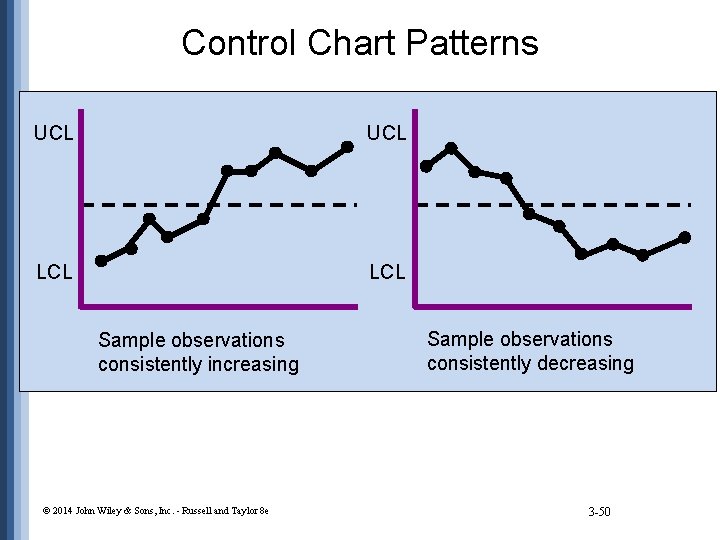
Control Chart Patterns • Run • sequence of sample values that display same characteristic • Pattern test • determines if observations within limits of a control chart display a nonrandom pattern © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -47

Control Chart Patterns • To identify a pattern look for: • • 8 consecutive points on one side of the center line 8 consecutive points up or down 14 points alternating up or down 2 out of 3 consecutive points in zone A (on one side of center line) • 4 out of 5 consecutive points in zone A or B (on one side of center line) © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -48

Control Chart Patterns UCL LCL Sample observations consistently below the center line © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e Sample observations consistently above the center line 3 -49

Control Chart Patterns UCL LCL Sample observations consistently increasing © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e Sample observations consistently decreasing 3 -50

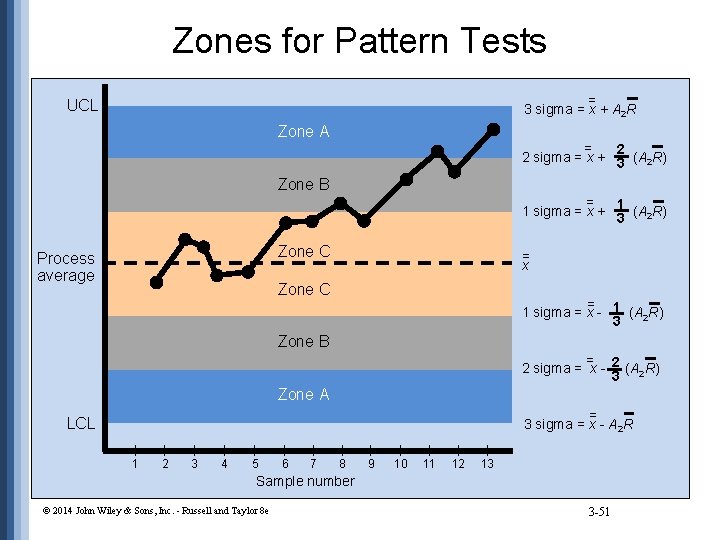
Zones for Pattern Tests = 3 sigma = x + A 2 R UCL Zone A = 2 2 sigma = x + 3 (A 2 R) Zone B = 1 1 sigma = x + 3 (A 2 R) Zone C Process average = x Zone C = 1 sigma = x - 1 (A 2 R) 3 Zone B = 2 sigma = x - 2 (A 2 R) 3 Zone A = 3 sigma = x - A 2 R LCL | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 Sample number © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -51

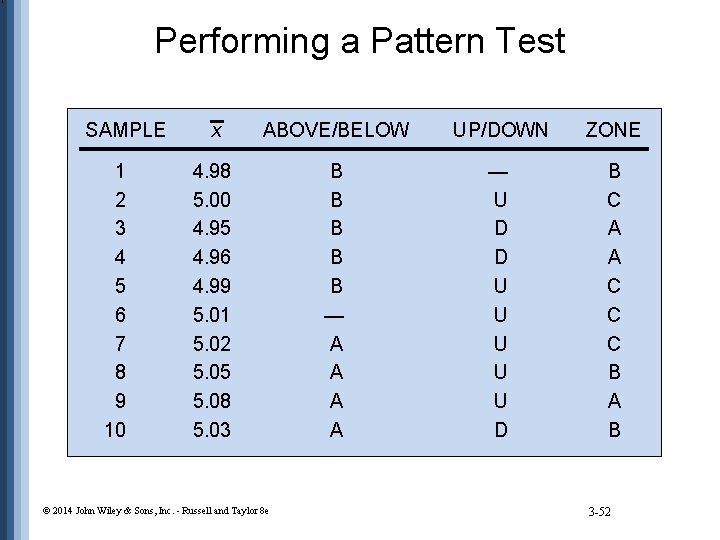
Performing a Pattern Test SAMPLE 1 2 3 4 5 6 7 8 9 10 x ABOVE/BELOW UP/DOWN ZONE 4. 98 5. 00 4. 95 4. 96 4. 99 5. 01 5. 02 5. 05 5. 08 5. 03 B B B — A A — U D D U U U D B C A A C C C B A B © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -52

Sample Size Determination • Attribute charts require larger sample sizes • 50 to 100 parts in a sample • Variable charts require smaller samples • 2 to 10 parts in a sample © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -53

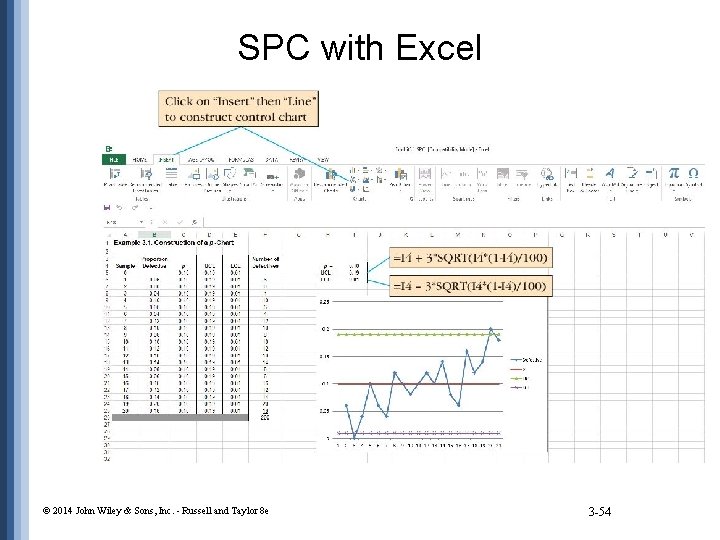
SPC with Excel © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -54

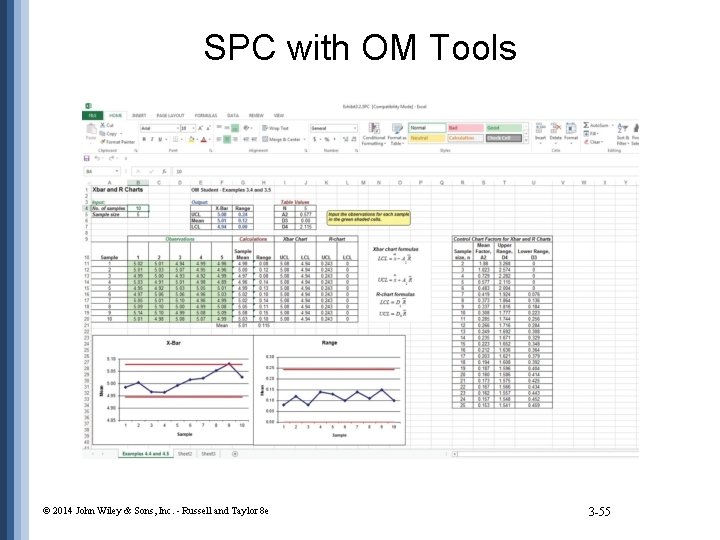
SPC with OM Tools © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -55

Process Capability • Compare natural variability to design variability • Natural variability • What we measure with control charts • Process mean = 8. 80 oz, Std dev. = 0. 12 oz • Tolerances • Design specifications reflecting product requirements • Net weight = 9. 0 oz 0. 5 oz • Tolerances are 0. 5 oz © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -56

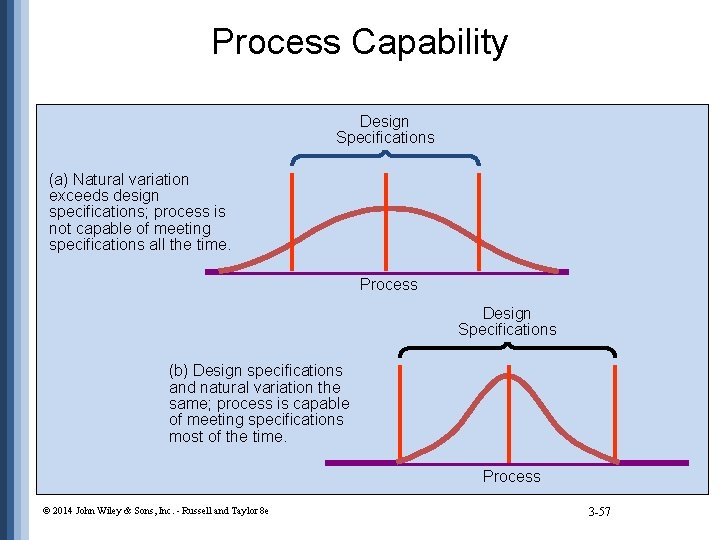
Process Capability Design Specifications (a) Natural variation exceeds design specifications; process is not capable of meeting specifications all the time. Process Design Specifications (b) Design specifications and natural variation the same; process is capable of meeting specifications most of the time. Process © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -57

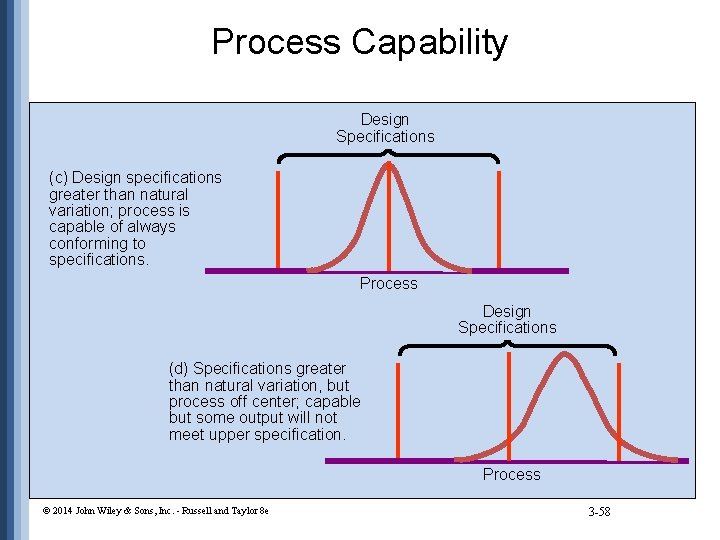
Process Capability Design Specifications (c) Design specifications greater than natural variation; process is capable of always conforming to specifications. Process Design Specifications (d) Specifications greater than natural variation, but process off center; capable but some output will not meet upper specification. Process © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -58

Process Capability Ratio Cp = = tolerance range process range upper spec limit - lower spec limit © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 6 3 -59

Computing Cp Net weight specification = 9. 0 oz 0. 5 oz Process mean = 8. 80 oz Process standard deviation = 0. 12 oz Cp = upper specification limit lower specification limit © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 6 3 -60

Computing Cp Net weight specification = 9. 0 oz 0. 5 oz Process mean = 8. 80 oz Process standard deviation = 0. 12 oz Cp = upper specification limit lower specification limit 6 9. 5 - 8. 5 = = 1. 39 6(0. 12) © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -61

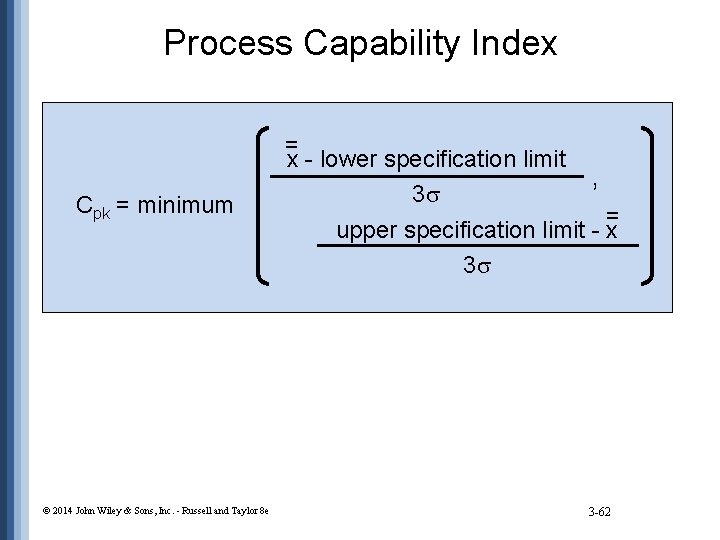
Process Capability Index Cpk = minimum © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e = x - lower specification limit 3 , = upper specification limit - x 3 3 -62

Computing Cpk Net weight specification = 9. 0 oz 0. 5 oz Process mean = 8. 80 oz Process standard deviation = 0. 12 oz Cpk = minimum © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e = x - lower specification limit , 3 = upper specification limit - x 3 3 -63

Computing Cpk Net weight specification = 9. 0 oz 0. 5 oz Process mean = 8. 80 oz Process standard deviation = 0. 12 oz Cpk = minimum = x - lower specification limit , 3 = upper specification limit - x 3 = minimum 8. 80 - 8. 50 9. 50 - 8. 80 , = 0. 83 3(0. 12) © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -64

Process Capability With Excel © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -65

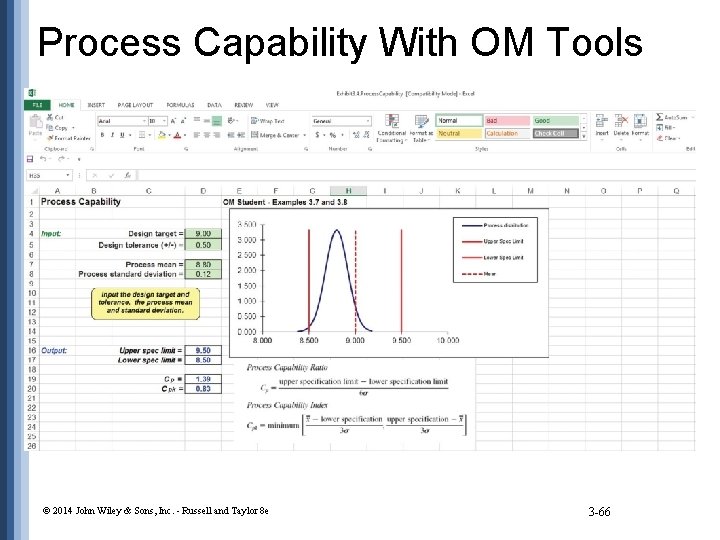
Process Capability With OM Tools © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -66

Copyright 2014 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in section 117 of the 1976 United States Copyright Act without express permission of the copyright owner is unlawful. Request for further information should be addressed to the Permission Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages caused by the use of these programs or from the use of the information herein. © 2014 John Wiley & Sons, Inc. - Russell and Taylor 8 e 3 -67