Chapter 3 Sets Combinatorics Section 3 1 Sets

Chapter 3. Sets & Combinatorics Section 3. 1 Sets · A set is an unordered collection of objects. (without repetition) ( the order in which the elements are written does not matter) e. g. {A, B, C, D} = {D, A, B, C} · Each element of a set is listed only once. CS 130 Young 1

· Various ways to describe a set: - Enumeration e. g. define the 12 months of a year - Use recursion e. g. 2 T If x T, then x+3 T and 2 x T (recursion covered in Section 2. 4) CS 130 Young 2

· describe a property P that characterizes the elements, e. g. S = {x| P(x)} means ( x) [ (x S P(x)) (P(x) x S) e. g. {x | x is an integer and 3 < x 7} = { 4, 5, 6, 7} e. g. {x | x is a month with exactly 30 days} = {Apr, Jun, Sep, Nov} e. g. Describe the set by giving the characteristic property. {1, 4, 9, 16} = {x | x is one of the first four perfect squares for positive integers} {2, 3, 5, 7, 11, 13, 17, …} = {x | x is a prime number} CS 130 Young 3

· Standard sets: N = set of all nonnegative integers ( 0 N ) Z = set of all integers Q = set of all rational numbers R = set of all real numbers C = set of all complex numbers e. g. S = {x | x N and x < 0 }, then S = {} = e. g. A = {x | x N and ( y)(y {2, 3, 4, 5} x y)} = {x |x N and x 5} e. g. B = {x | ( y)( z)(y {1, 2} and z {2, 3} and x = y + z)} = {3, 4, 5} CS 130 Young 4

· A is a subset of B, denoted by A B, if ( x)(x A x B). A is a proper subset of B, denoted by A B, if A B and A B. e. g. A = {1, 7, 9, 15} B = {7, 9} then B A 15 A {7, 9} B B CS 130 Young 5

· Power set of S, denoted by P(S) or 2 S, contains all of the subsets of S. P(S) and S P(S) are always true. e. g. S ={1, 2, 3}, P(S) = { , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} |P(S)| = 2|S| each element could be included or not to be included into a subset. CS 130 Young 6

· Operations on sets: 1. Union A B = {x | x A or x B} 2. Intersection A B = {x | x A and x B} 3. Difference A – B = {x | x A and x B} 4. Cartesian Product A B = {(x, y)| x A and y B} 5. Complement 6. A = {x | x S and x A} where S is the Universal Set CS 130 Young 7

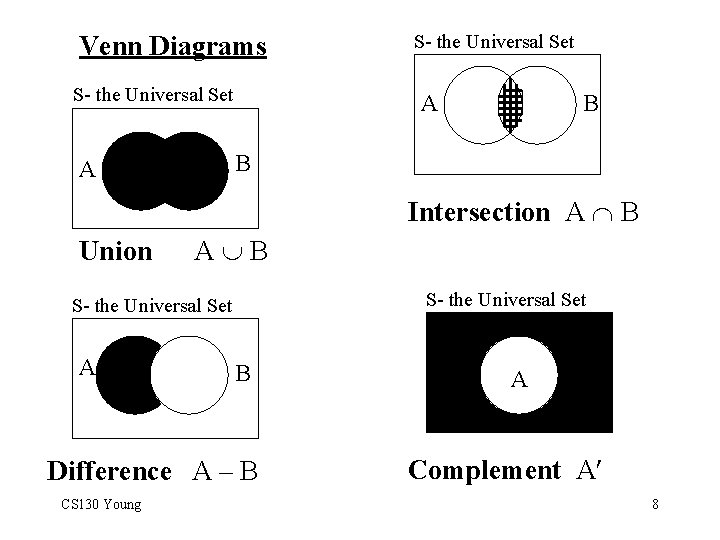
Venn Diagrams S- the Universal Set A B B A Intersection A B Union A B S- the Universal Set A B Difference A – B CS 130 Young A Complement A 8

e. g. A = {1, 2, 3, 5, 10} B = {2, 4, 7, 8, 9} C = {5, 8, 10} S (Universal Set ) = {1, 2, 3, 4, 5, 6 , 7 , 8, 9, 10} A B = {1, 2, 3, 4, 5, 7, 8, 9, 10} A – C = {1, 2, 3} B (A C) = {1, 3, 5, 6, 10} {1, 2, 3, 5, 8, 10} = {1, 3, 5, 10} [ Note: B , the complement of B, is {x | x S and x B} ] CS 130 Young 10

· Set Identities: 1) A B = B A commutative property 2) (A B) C = A (B C) associative property 3) A (B C) = (A B) (A C) CS 130 Young distributive property 11

4) A = A 5) A S=A 5) A A = S A A = CS 130 Young identity property complement property 12