Chapter 3 Section 6 Copyright 2008 Pearson Education

3. 6 1 2 3 4 5 6 Introduction to Functions Understand the definition

Objective 1 Understand the definition of a relation. Copyright © 2008 Pearson Education, Inc.

Understand the definition of a relation. In an ordered pair (x, y), x and

EXAMPLE 1 Identifying Domains and Ranges of Relations Defined by Ordered Pairs Use ordered

Objective 2 Understand the definition of a function. Copyright © 2008 Pearson Education, Inc.

Understand the definition of a function. A very important type of relation called a

EXAMPLE 2 Determining Whether Relations Are Functions Determine whether each relation is a function.

Objective 3 Decide whether an equation defines a function. Copyright © 2008 Pearson Education,

Decide whether an equation defines a function. Given the graph of an equation, the

EXAMPLE 3 Deciding Whether Relations Define Functions Determine whether each relation is a function.

Objective 4 Find domains and ranges. Copyright © 2008 Pearson Education, Inc. Publishing as

Find domains and ranges. By the definitions of domain and range given for relations,

EXAMPLE 4 Finding the Domain and Range of Functions Find the domain and range

Objective 5 Use function notation. Copyright © 2008 Pearson Education, Inc. Publishing as Pearson

Use function notation. The letters f, g, and h are commonly used to name

Function Notation In the notation f(x), f is the name of the function, x

EXAMPLE 5 Using Function Notation For the function f (x) = 6 x −

Objective 6 Apply the function concept in an application. Copyright © 2008 Pearson Education,

EXAMPLE 6 Applying the Function Concept to Population The number of U. S. students

EXAMPLE 6 Applying the Function Concept to Population (cont’d) The number of U. S.

Slides: 21

Download presentation

3. 6 1 2 3 4 5 6 Introduction to Functions Understand the definition of a relation. Understand the definition of a function. Decide whether an equation defines a function. Find domains and ranges. Use function notation. Apply the function concept in an application. Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

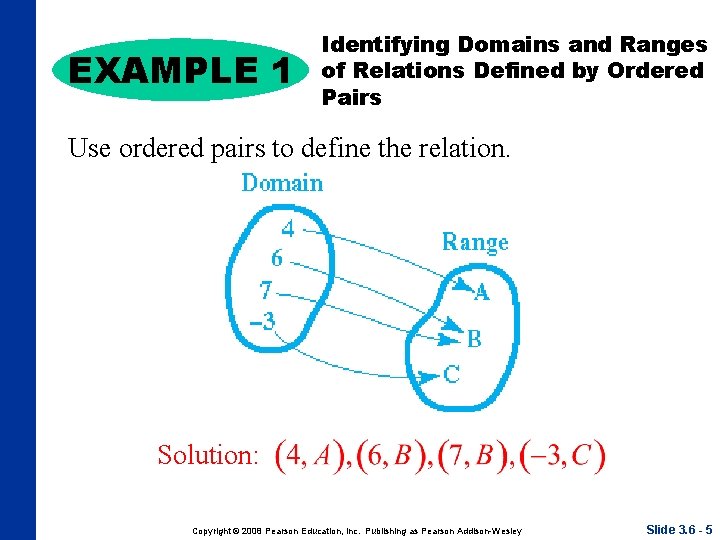
Understand the definition of a relation. In an ordered pair (x, y), x and y are called the components of the ordered pair. Any set of ordered pairs is called a relation. The set of all first components of the ordered pairs of a relation is the domain of the relation, and the set of all second components of the ordered pairs is the range of the relation. Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 4

EXAMPLE 1 Identifying Domains and Ranges of Relations Defined by Ordered Pairs Use ordered pairs to define the relation. Solution: Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 5

Understand the definition of a function. A very important type of relation called a function. A function is a set of ordered pairs in which each first component corresponds to exactly one second component. By definition, the relation in the following order pairs is not a function, because the same first component, 3, corresponds to more then one second component. If the ordered pairs from this example were interchanged, giving the relation the result would be a function. In that case, each domain (first component) corresponds to exactly one range element (second component). Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 7

EXAMPLE 2 Determining Whether Relations Are Functions Determine whether each relation is a function. Solution: function Solution: not a function Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 8

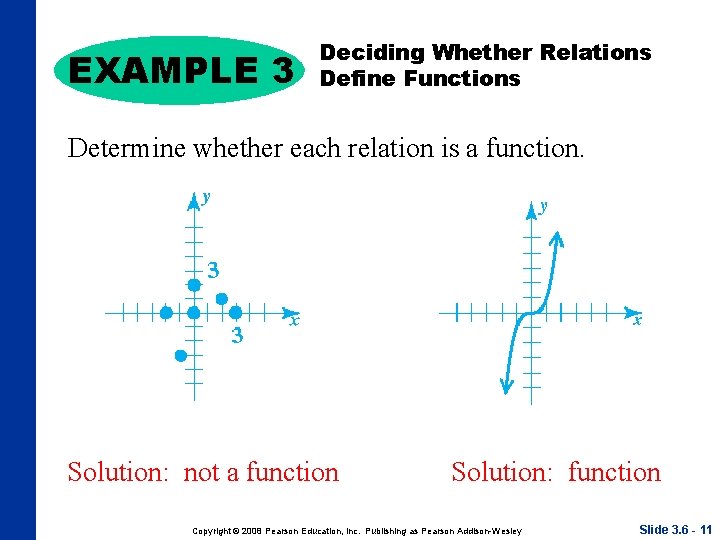
Decide whether an equation defines a function. Given the graph of an equation, the definition of a function can be used to decide whether or not the graph represents a function. By the definition of a function , each x-value must lead to exactly one y-value. The way to determine if a graph is a function is the vertical line test. If a vertical line intersects a graph in more than one point, then the graph is not the graph of a function. Any nonvertical line is the graph of a function. For this reason, any linear equation of the form y = mx + b defines a function. (Recall that a vertical line has an undefined slope. ) Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 10

EXAMPLE 3 Deciding Whether Relations Define Functions Determine whether each relation is a function. Solution: not a function Solution: function Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 11

Find domains and ranges. By the definitions of domain and range given for relations, the set of all numbers that can be used as replacements for x in a function is the domain of the function. The set of all possible values of y is the range of the function. Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 13

EXAMPLE 4 Finding the Domain and Range of Functions Find the domain and range of the function y = x 2 + 4. Solution: Domain: Range: Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 14

Use function notation. The letters f, g, and h are commonly used to name functions. For example, the function y = 3 x + 5 may be written where f (x) is read “f of x. ” The notation f (x) is another way of writing y in a function. For the function defined by f (x) = 3 x + 5, if x = 7, then Read this result, f (7) = 26, as “f of 7 equals 26. ” The notation f (7) means the values of y when x is 7. The statement f (7) = 26 says that the value of y = 26 when x is 7. It also indicates that the point (7, 26) lies on the graph of f. The notation f(x) does not mean f times x; f(x) means the value of x for the function f. It represents the y –value that Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 16

Function Notation In the notation f(x), f is the name of the function, x is the domain value, and f(x) is the range value y for the domain value x. Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 17

EXAMPLE 6 Applying the Function Concept to Population The number of U. S. students ages 3 – 21 served by educational programs for students with disabilities for selected years are given in the table. a) Write a set of ordered pairs that defines a function f for these data. b) Give the domain and range of f. c) Find f (1998). d) In which year did the number of students equal 5. 7 million? That is, for what value of x does f (x) = 5. 7 million? Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 20

EXAMPLE 6 Applying the Function Concept to Population (cont’d) The number of U. S. students ages 3 – 21 served by educational programs for students with disabilities for selected years are given in the table. Solution: a) b) c) d) Copyright © 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 3. 6 - 21